Физические основы гемодинамики. (Лекция 4)

1. лекция № 4 для студентов 1 курса, обучающихся по специальности 31.05.01 – Лечебное дело К.п.н., доцент Шилина Н.Г. Красноярск, 2016

Кафедра медицинской и биологической физики
Тема: Физические основы
гемодинамики
лекция № 4
для студентов 1 курса, обучающихся по специальности
31.05.01 – Лечебное дело
К.п.н., доцент Шилина Н.Г.
Красноярск, 2016

2. План лекции:

1.
2.
3.
4.
5.
6.
Идеальная жидкость. Уравнение Бернулли.
Вязкость жидкости. Уравнение Ньютона.
Течение вязкой жидкости. Формула Гаагена –
Пуазейля.
Реологические свойства крови.
Методы измерения вязкости жидкостей.
Работа и мощность сердца. Модели
кровообращения.

3.

Реологией называется область
механики,
которая
изучает
деформационные
(реологические)
свойства жидкостей, газов и твердых
тел, способы установления и описания
этих свойств, а отчасти и их
физическую природу.

4.

Жидкость несжимаемая и не
имеющая внутреннего трения
называется идеальной.
Течение, при котором скорости
частиц жидкости в каждой точке
потока
со
временем
не
изменяются,
называется
стационарным.

5.

S
1
2
21
Воображаемые линии, совпадающие с
траекториями частиц, называются линиями
тока.
Часть потока жидкости, ограниченного со
всех сторон линиями тока, образует трубку
тока или струю.
S1·v1= S2·v2
или
S·v=Const
– условие неразрывности
струи

6. Вывод уравнения Бернулли

m
m
1
Е
2 2 SL SL
2
2
2
2
1
К 211
Вывод уравнения Бернулли
V1=V2; S1L1= S2L2;
Работа сил, оказывающих давление:
Ад=F1L1 – F2L2=P1S1L1 – P2S2L2
Работа силы тяжести:
АТ=mgh1 – mgh2 =ρS1L1gh1 – ρS2L2gh2
Изменение кинетической энергии при
движении объема жидкости:

7.

12 SP
2
2
L
S
L
2P
1
2
g
h
P
g
h
11
1
2
2
2
2
2
12
gh1 C
onst
т.к. Ад+ АТ =ΔЕК , то
P1S1L1 – P2S2L2 + ρS1L1gh1 – ρS2L2gh2 =
и S1L1= S2L2
т.к. сечение выбрано произвольно, то
- уравнение Бернулли

8.

P
2 gh C
onst
2
1
11
При стационарном течении идеальной
жидкости (υ=Const) полное давление,
равное сумме статического,
гидростатического и динамического
давлений, остается постоянным в
любом поперечном сечении потока.

9. Следствия из уравнения Бернулли

2
2
1
P
P
2
12
2
Следствия из уравнения
Бернулли
Наклонная трубка постоянного сечения
Р1 + ρgh1 = Р2 + ρgh2 ; Р1 – Р2 = ρg(h1 - h2)
Горизонтальная трубка переменного
сечения
т.к. S2 < S1 , то v2 > v1
и Р 2 < Р1
Статическое давление невязкой жидкости при
течении по горизонтальной трубе возрастает
там, где скорость ее уменьшается.

10. ВЯЗКОСТЬ ЖИДКОСТИ

Способность реальных жидкостей
оказывать сопротивление движению в
них тел или собственному течению за
счет
сил
межмолекулярного
взаимодействия
называется
внутренним
трением
или
вязкостью жидкости.

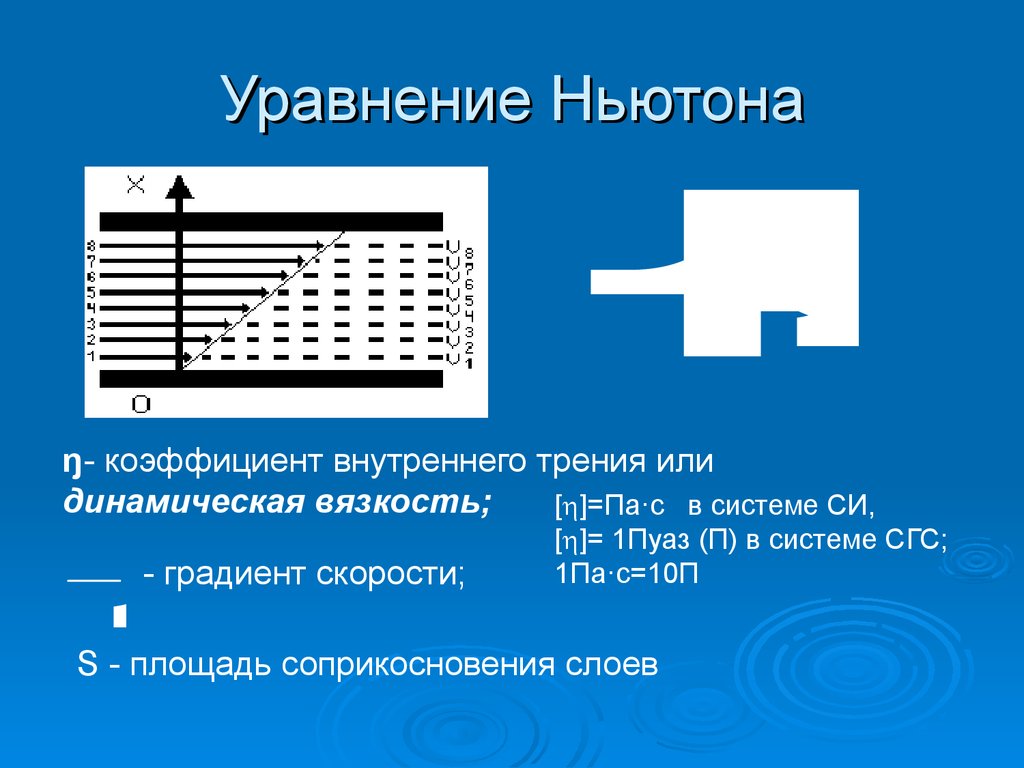
11. Уравнение Ньютона

d
υ
F
η
S
т
р
x
d
υ
x
Уравнение Ньютона
ŋ- коэффициент внутреннего трения или
динамическая вязкость;
[ ]=Па·с в системе СИ,
- градиент скорости;
[ ]= 1Пуаз (П) в системе СГС;
1Па·с=10П
S - площадь соприкосновения слоев

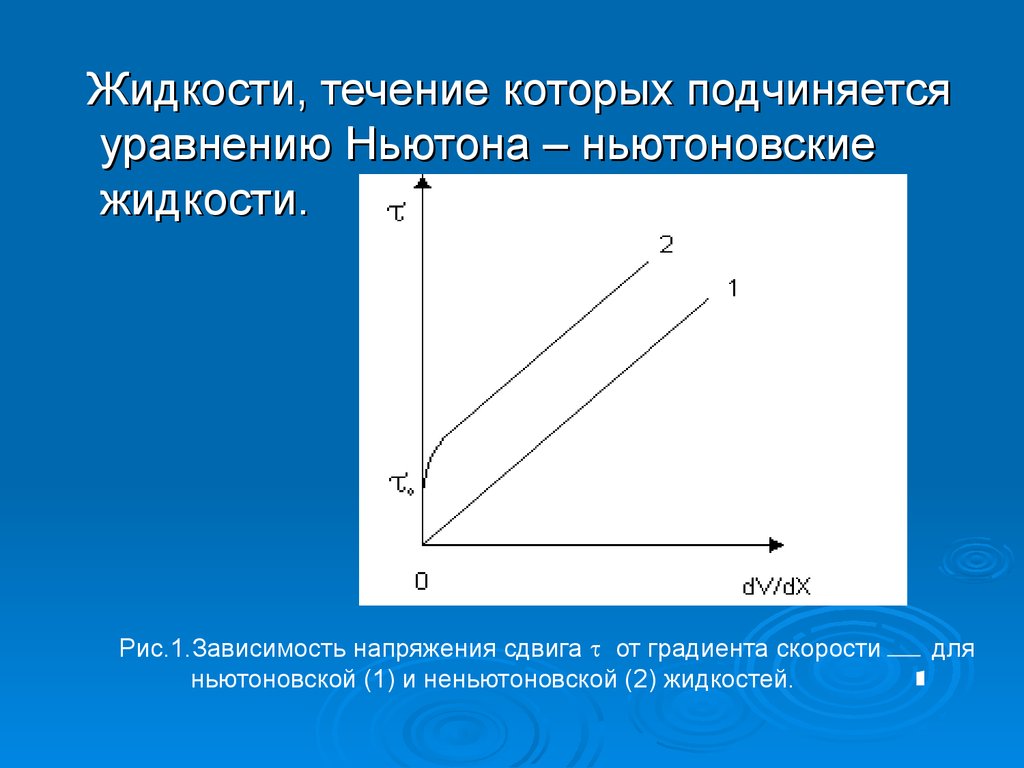
12.

d
υ
x
Жидкости, течение которых подчиняется
уравнению Ньютона – ньютоновские
жидкости.
Рис.1.Зависимость напряжения сдвига от градиента скорости
ньютоновской (1) и неньютоновской (2) жидкостей.
для

13. Относительная вязкость крови

живдкоысти
Относительная вязкость крови
НОРМА
АНЕМИЯ
ПОЛИЦИТАМИЯ
МУЖЧИНЫ
ЖЕНЩИНЫ
4,2 – 6
2–3
15 – 20
4,3 – 1,7
3,9 – 4,9
Вязкость крови зависит от концентрации
эритроцитов и белков плазмы, от
их состава , от размеров клеток крови,
эластичности мембран эритроцитов.
- относительная вязкость

14. КЛАССИФИКАЦИЯ БИОЛОГИЧЕСКИХ ЖИДКОСТЕЙ

Вязкость не зависит от градиента скорости –
ньютоновская жидкость.
Вязкость уменьшается с увеличением градиента
скорости – псевдопластическое вещество.
Вязкость увеличивается с увеличением градиента
скорости – дилатантное вещество.
Вязкость уменьшается при продолжительном
вращении, но после остановки возвращается к
исходному значению – тиксотропное вещество
(жидкость Бингама).
Вязкость возрастает при продолжительном
вращении, но после остановки возвращается к
исходному значению – реопексное вещество.

15. Нелинейно вязкие жидкости

0
Нелинейно вязкие жидкости
Реологические кривые для ньютоновской (1), псевдопластической
(2), дилатантной (3), вязко-пластической (4) жидкостей
3
4
3
1
4
1
2
2

16. ФОРМУЛА ПУАЗЕЙЛЯ

Стационарное (слоями) течение жидкостей
называется ламинарным.
Рис.2. Распределение скоростей частиц жидкости
по сечению трубы.

17.

ρ
υ
D
R
e
η
Характер течение жидкости по трубе
зависит от ее поверхности, диаметра
D, от свойств жидкости (плотности и
вязкости ), ее скорости v.
Течение с завихрениями при
смешивании
слоев
называется
турбулентным.
- число Рейнольдса
Если Re > Reкрит – движение турбулентное.
- кинематическая вязкость (Стокс)

18. Формула Пуазейля

υm axP14 1L2 P(2R2 2r2)
Формула Пуазейля
Скорость протекания жидкости по трубе
v зависит от разности давлений (Р1-Р2)
на концах трубы, ее длины L, радиуса R
и вязкости жидкости:
- в центре трубы

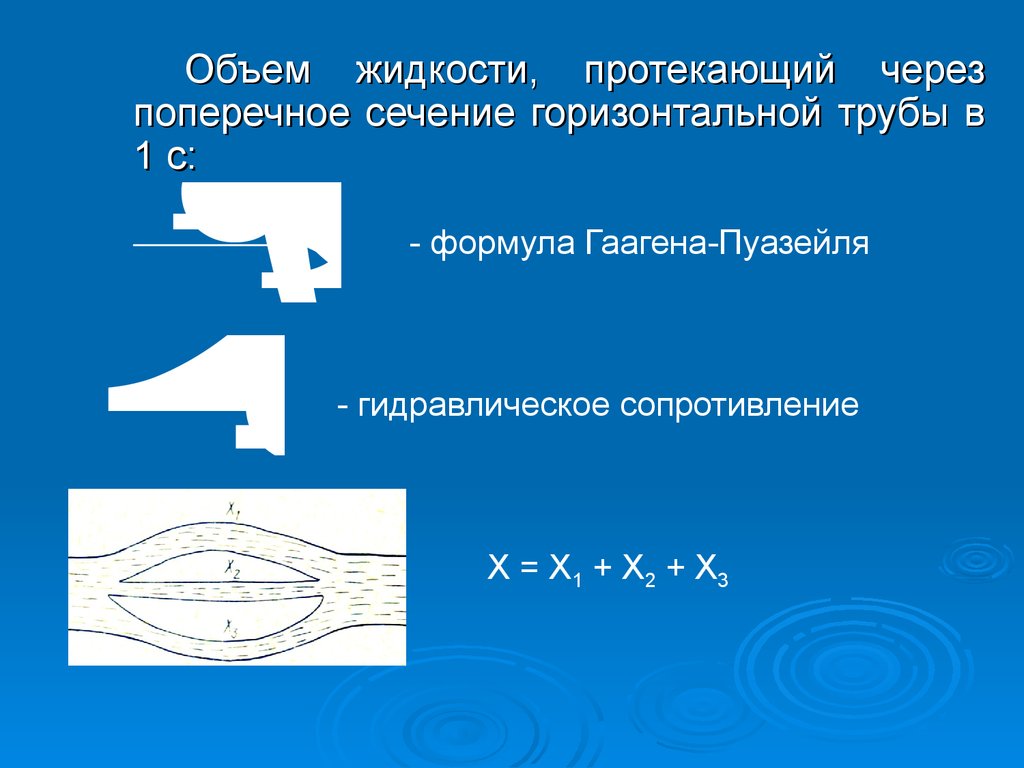
19.

4
QX
π8
π
R
P
1
2
L
L
4
R
Объем жидкости, протекающий через
поперечное сечение горизонтальной трубы в
1 с:
- формула Гаагена-Пуазейля
- гидравлическое сопротивление
Х = Х1 + Х2 + Х3

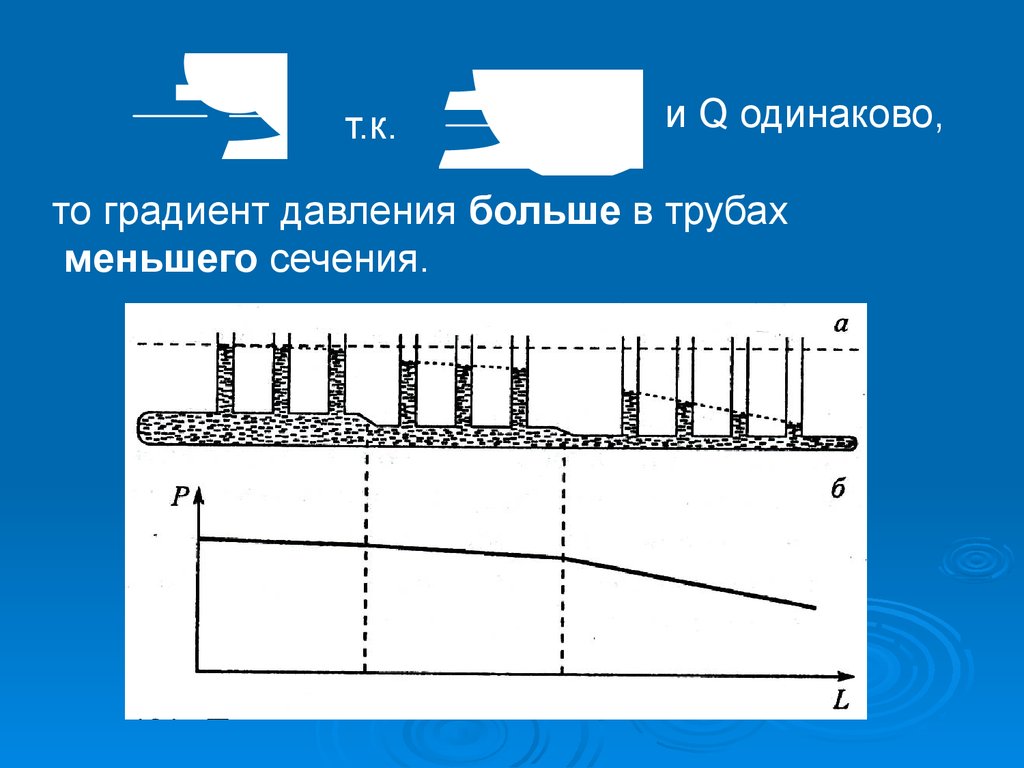
20.

4
π
R
d
P
Q
8
LdP
sLt
C
o
n
т.к.
и Q одинаково,
то градиент давления больше в трубах
меньшего сечения.

21. МЕТОДЫ ИЗМЕРЕНИЯ ВЯЗКОСТИ ЖИДКОСТИ

2
ρ
2
Ж
η 9gR
V
МЕТОДЫ ИЗМЕРЕНИЯ
ВЯЗКОСТИ ЖИДКОСТИ
Метод Стокса

22. Метод капиллярного вискозиметра

π
R
Δ
P
Q
t
8
η
L
tη
ρ
4
x
4
0
x
x00
Метод капиллярного
вискозиметра

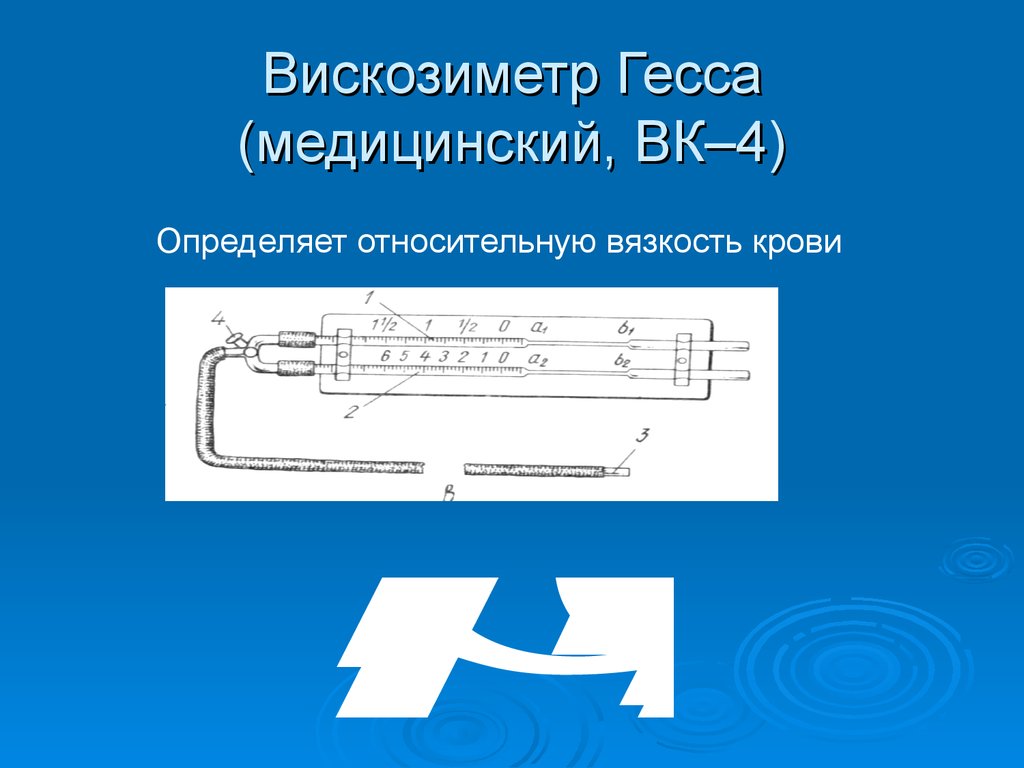
23. Вискозиметр Гесса (медицинский, ВК–4)

l
в
к
р
в
к
р
Вискозиметр Гесса
(медицинский, ВК–4)
Определяет относительную вязкость крови

24.

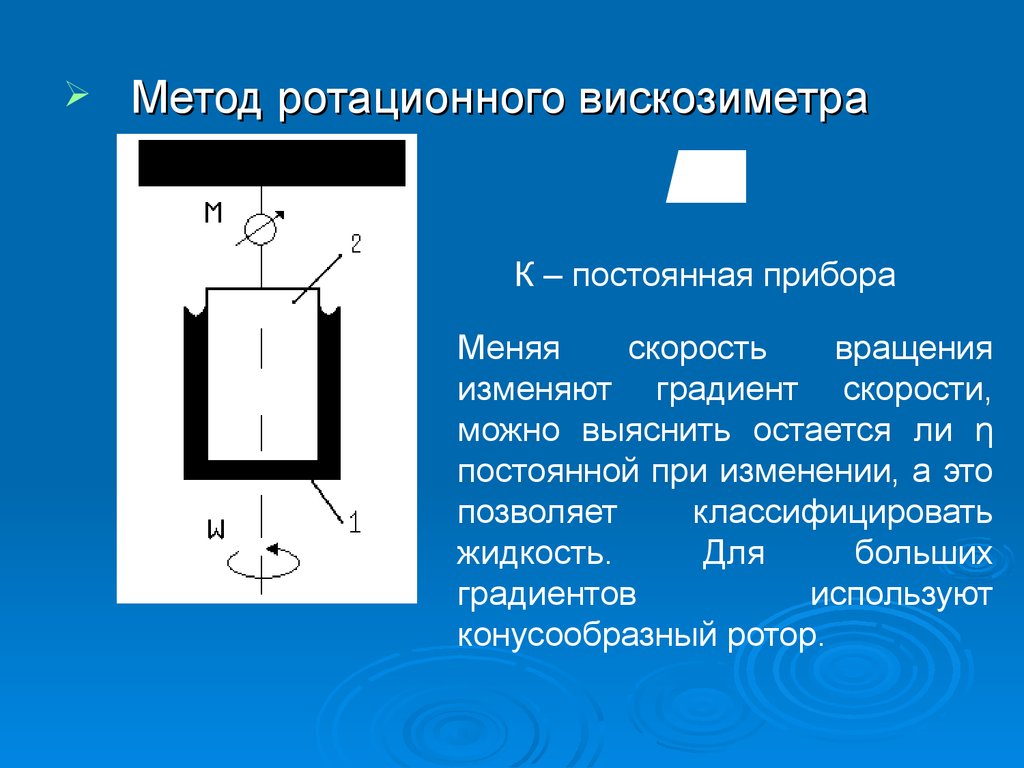
к
Метод ротационного вискозиметра
К – постоянная прибора
Меняя
скорость
вращения
изменяют градиент скорости,
можно выяснить остается ли η
постоянной при изменении, а это
позволяет
классифицировать
жидкость.
Для
больших
градиентов
используют
конусообразный ротор.

25. РАБОТА И МОЩНОСТЬ СЕРДЦА

Работа сил давления А1= FL=PSL=PVуд
Кинетическая энергия А2= mυ2/2=ρVудυ2/2
Aл = А1+ А2= PVуд+ ρVудυ2/2
Ап=0,2 Aл ; А= Aл+ Ап=1,2Aл
A=1,2 (PVуд+ ρVудυ2/2)
Р=13 кПа; Vуд=60 мл =6·10-5 м3; υ=0,5 м/с;
ρ=1,05103 кг/м3
A ≈ 1 Дж; Продолжительность систолы 0,3с,
следовательно, мощность сердца А/t=3,3 Вт.

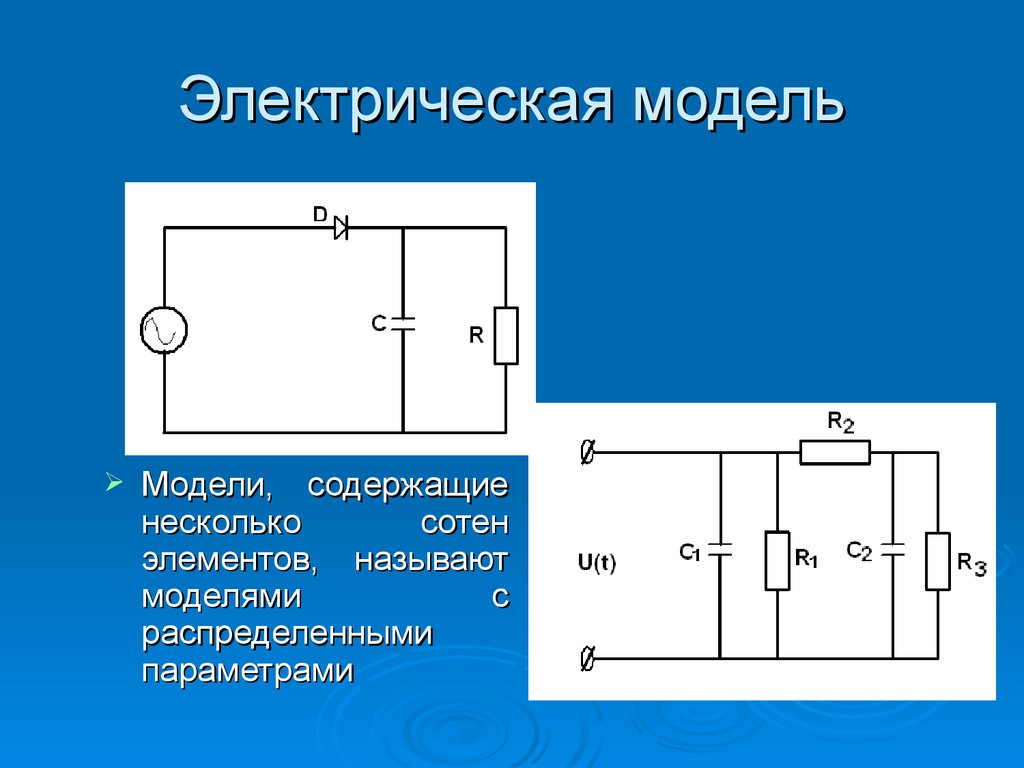
26. Модели кровообращения

Модель Франка (упругий резервуар)
Электрическая модель
Модель с распределенными
параметрами

27. Модель Франка

Р
e
Q
t00k
x0kxt0
Модель Франка
Зависимость давления в резервуаре после систолы
K – эластичность стенок;
х0 – сопротивление периферических сосудов.
Скорость оттока крови

28. Зависимость давления от времени за период сокращения

29. Электрическая модель

Модели, содержащие
несколько
сотен
элементов, называют
моделями
с
распределенными
параметрами

30. Пульсовая волна

x
Р
e
c
o
s
(
t
)
E
h
d
х
0
Пульсовая волна
уравнение гармонической
пульсовой волны
Формула Моенса–Кортевега
Е – модуль упругости;
ρ – плотность вещества;
h – толщина стенки сосуда;
d – диаметр сосуда.

31. Заключение:

Нами рассмотрены:
понятия идеальной и реальной жидкости, а
также уравнения, описывающие их
поведение;
2. методы измерения вязкости жидкостей.
3. реологические свойства крови.
4. Модели кровообращения (Франка,
электрическая модель и модель с
распределенными параметрами).
1.

32. Тест-контроль

Наибольший коэффициент вязкости из
перечисленных жидкостей имеет:
1. вода
2. лимфа
3. кровь
4. плазма.

33. РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Обязательная:
Ремизов А.Н. Медицинская и биологическая физика: учебник. -М.: Дрофа, 2007.Дополнительная:
Федорова В.Н. Краткий курс медицинской и биологической физики с элементами
реабилитологии: учебное пособие. -М.: Физматлит, 2005.
Антонов В.Ф. Физика и биофизика. Курс лекций: учебное пособие.-М.: ГЭОТАР-Медиа,
2006.
Богомолов В.М. Общая физиотерапия: учебник. -М.: Медицина, 2003.
Самойлов В.О. Медицинская биофизика: учебник. -СПб.: Спецлит, 2004.
Руководство к лабораторным работам по медицинской и биологической физике для
самост. работы студентов /сост. О.Д. Барцева и др. Красноярск: Литера-принт, 2009.
Сборник задач по медицинской и биологической физике: учебное пособие для самост.
работы студентов / сост. О.П.Квашнина и др. -Красноярск: тип.КрасГМА, 2007.
Физика. Физические методы исследования в биологии и медицине: метод. указания к
внеаудит. работе студентов по спец. – педиатрия / сост. О.П.Квашнина и др. -Красноярск:
тип.КрасГМУ, 2009.Электронные ресурсы:
ЭБС КрасГМУ
Ресурсы интернет
Электронная медицинская библиотека. Т.4. Физика и биофизика.- М.: Русский врач, 2004.

34. БЛАГОДАРЮ ЗА ВНИМАНИЕ