Примеры программирования базовых алгоритмов циклических вычислительных процессов (ЦВП)

1. Примеры программирования базовых алгоритмов циклических вычислительных процессов (ЦВП)

2. Базовые алгоритмы ЦВП

• Организация счетчика
• Накопление суммы и произведения
• Поиск минимального (максимального)
значений

3. Задача. Алгоритм организации счетчика

Дана последовательность:
sinx+cos2x; sin3x+cos4x; …; sin11x+cos12x,
где x=π/6. Вычислить количество положительных
членов последовательности.
Для реализации алгоритма используются следующие
операторы присваивания:
L 0; {Начальная установка}
L L+1; {Организация счета}
Перед программированием данной задачи надо представить
последовательность в общем виде:
y(n)=sin((2n−1)x)+cos((2n)x); n=1, 2, …, 6

4. Задача. Алгоритм организации счетчика

CH( k)
x
6
L 0
for n 1 k
y sin [ ( 2 n 1) x] cos [ ( 2 n) x]
L L 1 if y 0
L
CH( 6) 3

5. Задача. Алгоритм накопления суммы

Дана функция:
y ( x 1)e
x
для x, изменяющегося от −2 до 2 с шагом 0,2.
Вычислить сумму тех значений функции, которые
удовлетворяют условию y≤0,5.
Для реализации алгоритма используются
следующие операторы присваивания:
S 0; {Начальная установка}
S S+y; {Накопление суммы}

6. Задача. Алгоритм накопления суммы

SUM( a )
S 0
for x 2 1.8 2
y ( x 1) e
x
S S y if y a
S
SUM( 0.5) 0.164

7. Задача. Алгоритм накопления произведения

Вычислить произведение ненулевых
последовательности:
z(k)=sink+cosk; k=1, 2, …, 10
принадлежащих интервалу [−0,5; 0,5].
Для реализации алгоритма используются
следующие операторы присваивания:
P 1; {Начальная установка}
P P*a; {Накопление произведения}
членов

8. Задача. Алгоритм накопления произведения

PR( n a b)
P 1
for k 1 n
z sin ( k) cos ( k)
P P z if ( z 0) ( a z b)
P
Вопрос. Какой результат может
быть выведен на экран, если
опустить начальную установку
алгоритма (P 1)?
PR( 10 0.5 0.5) 0.246

9. Алгоритм поиска максимального и минимального значений

Задача (Пример обработки одномерного массива)
Дан массив А=(2, -6, 10, 3.25, 0).
Вычислить величину r=m12 – m22, где
m1 – максимальный элемент массива;
m2 – минимальный элемент массива.

10. Алгоритм поиска максимального и минимального элементов массива

ORIGIN 1
MaxMin ( A n)
m1 10 6
m2 10 6
for
i 1 n
m1 Ai
if
Ai m1
m2 Ai
if
Ai m2
r m1 2 m2 2
r
2
6
A 10
3
0
MaxMin ( A 5) 64

11.

Алгоритмы обработки матриц можно
условно разделить на два типа.

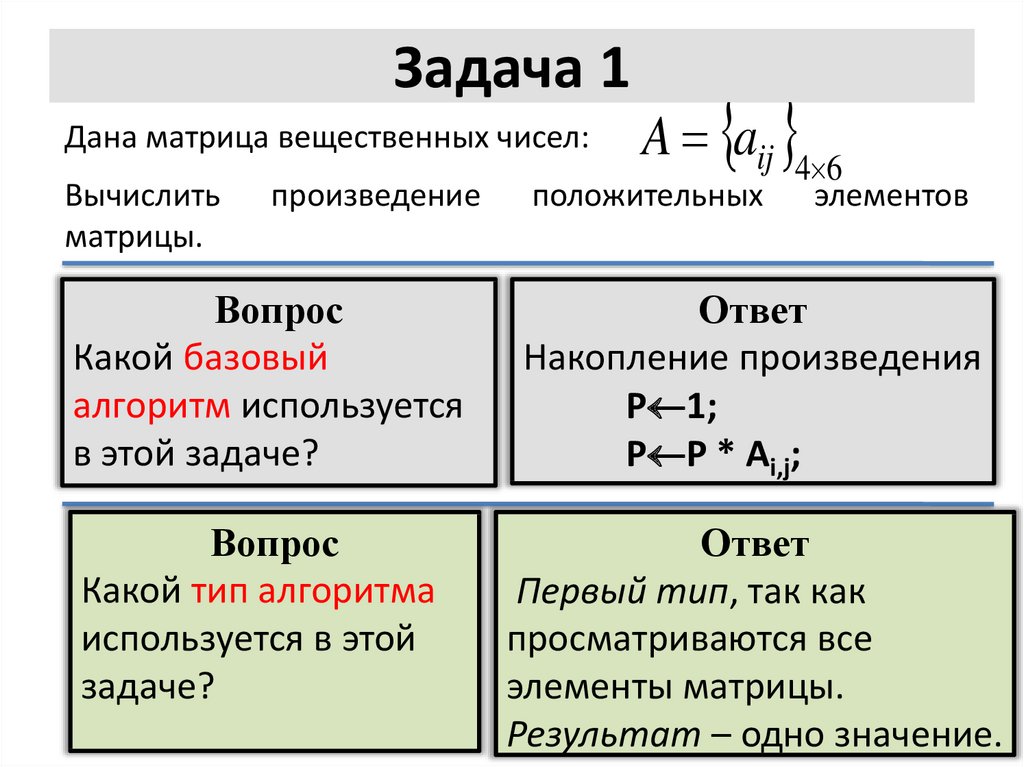
12. Задача 1

Дана матрица вещественных чисел:
Вычислить
матрицы.
произведение
A aij 4 6
положительных
элементов
Вопрос
Какой базовый
алгоритм используется
в этой задаче?
Ответ
Накопление произведения
P 1;
P P * Ai,j;
Вопрос
Какой тип алгоритма
используется в этой
задаче?
Ответ
Первый тип, так как
просматриваются все
элементы матрицы.
Результат – одно значение.

13. Задача 1 (Первый тип алгоритма обработки матрицы)

ORIGIN 1
Z1 ( A m n)
P 1
for i 1 m
for j 1 n
P P Ai j if Ai j 0
P
1 2 3 4 5 6
7 8 9 0 9 8
A
7 6 5 4 3
2
1 0 1 2 3 4
Z1 ( A 4 6) 144

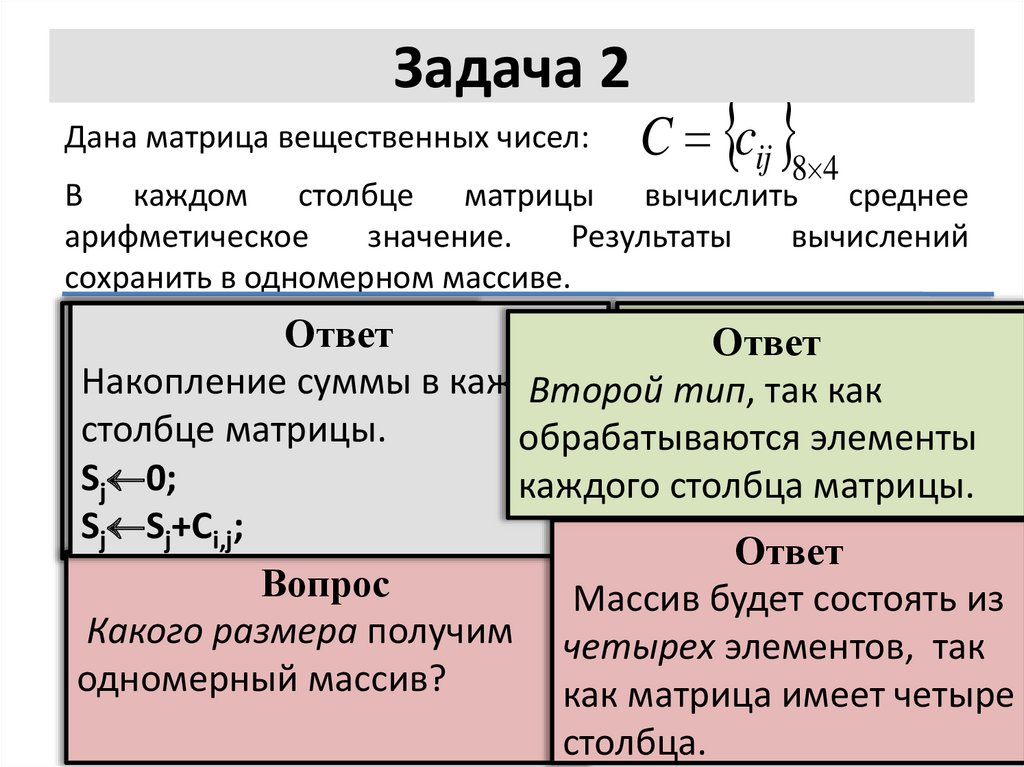
14. Задача 2

Дана матрица вещественных чисел:
C cij 8 4
В каждом столбце матрицы вычислить среднее
арифметическое
значение.
Результаты
вычислений
сохранить в одномерном массиве.
Вопрос
Ответ
Вопрос
Ответ
Какой
Накопление
базовый
суммы в каждом
Какой
Второй
тип,тип
такалгоритма
как
алгоритм
столбце матрицы.
используется обрабатываются
используется
в этой
элементы
вSjэтой
задаче?
0; задаче?
каждого
столбца матрицы.
Sj Sj+Ci,j;
Ответ
Вопрос
Массив будет состоять из
Какого размера получим четырех элементов, так
одномерный массив?
как матрица имеет четыре
столбца.

15. Задача 2 (Второй тип алгоритма обработки матрицы)

ORIGIN 1
Z2 ( C)
for j 1 4
Sj 0
for i 1 8
Sj Sj Ci j
Sj
Sj
8
S
3.375
3.875
Z2 ( C)
5.625
3.75
1
2
3
4
C
1
5
2
9
1
2
3
4
2
6
8
5
1
1
2 2
3 3
4 4
3 4
7 8
3 7
22 1