Similar presentations:
Адсорбция
1. АДСОРБЦИЯ
Адсорбция – это изменение концентрациивещества вблизи поверхности раздела фаз
( термин происходит от лат. аd-на и sorbeoпоглощаю).
Адсорбция представляет собой
самопроизвольный процесс перераспределения
компонентов между поверхностным слоем и
объемными фазами.
Обратный процесс перехода вещества из
поверхностного слоя в объемную фазу называют
десорбцией. В соответствии с основным
постулатом термодинамики в изолированной
системе устанавливается динамическое
равновесие (адсорбционное равновесие) между
адсорбцией и десорбцией
2.
3.
Более плотная фаза (определяющаяформу поверхности) называется
адсорбентым (обычно адсорбент это
твердая или жидкая фаза)
Вещество которое перераспределяется
(жидкая или газообразная фаза) называется
адсорбатом
4.
Адсорбция может происходить на любойповерхности раздела между фазами. В
зависимости от агрегатного состояния смежных
фаз различают адсорбцию газов на твердых
адсорбентах, адсорбцию растворенных веществ
на границах твердое тело – жидкость и жидкость
– жидкость, а также адсорбцию на границе
жидкий раствор – газ.
Адсорбция является одним из механизмов
снижения свободной поверхностной энергии. В
результате притяжения поверхностью раздела
фаз находящихся вблизи нее молекул адсорбата
свободная поверхностная энергия уменьшается,
т. е. процессы адсорбции энергетически
выгодны.
5.
6.
7.
8.
9.
10.
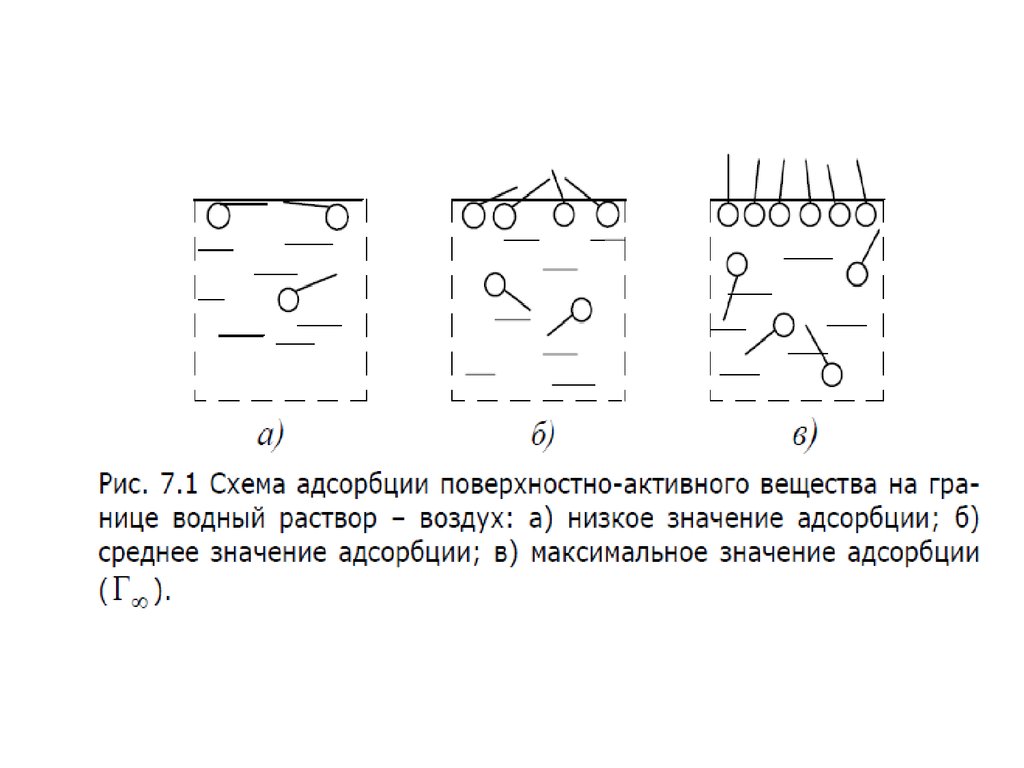
11. Величины адсорбции
На рисунке приведены графики зависимости , где концентрация
го компонента; координата вдоль соприкасающихся фаз. На
графиках представлена системы состоящие из двух фаз. Линия
– сечение межфазной поверхности. Координаты и
соответствуют границам поверхностного слоя.
– График а - система со слабосорбирующимся компонентом; график
б - с сильносорбирующимся компонентом.
12.
Рассмотрим объединенное уравнение I и II законов термодинамики воткрытой системе с учетом энергии поверхностного натяжения и
изменения химических потенциалов для изохорного процесса
dU TdS dS пов i d i
i
После интегрирования получим:
U TS S пов i i
i
Запишем выражение для полного дифференциала U
:
dU TdS SdT dSпов S пов d i d i i d i
i
dU получим
SdT S пов d i i d i 0
Приравнивая выражение для
i
i
13.
T constВ случае
получим выражение
S пов d i i d i 0
i
Учитывая, что
Получим
Гиббса:
i
i
S пов
фундаментальное
адсорбционное
уравнение
d i d i
i
Зависимость поверхностного натяжения от адсорбции одного
компонента, при постоянстве химических потенциалов других
компонентов.
Г i
i j
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
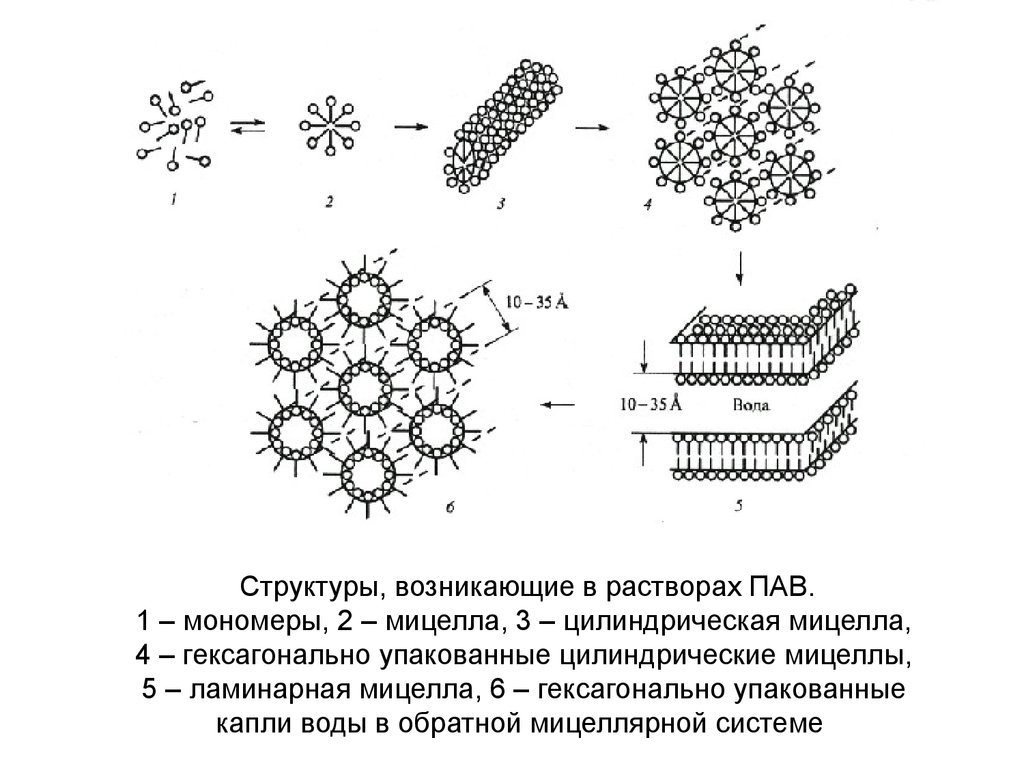
Структуры, возникающие в растворах ПАВ.1 – мономеры, 2 – мицелла, 3 – цилиндрическая мицелла,
4 – гексагонально упакованные цилиндрические мицеллы,
5 – ламинарная мицелла, 6 – гексагонально упакованные
капли воды в обратной мицеллярной системе
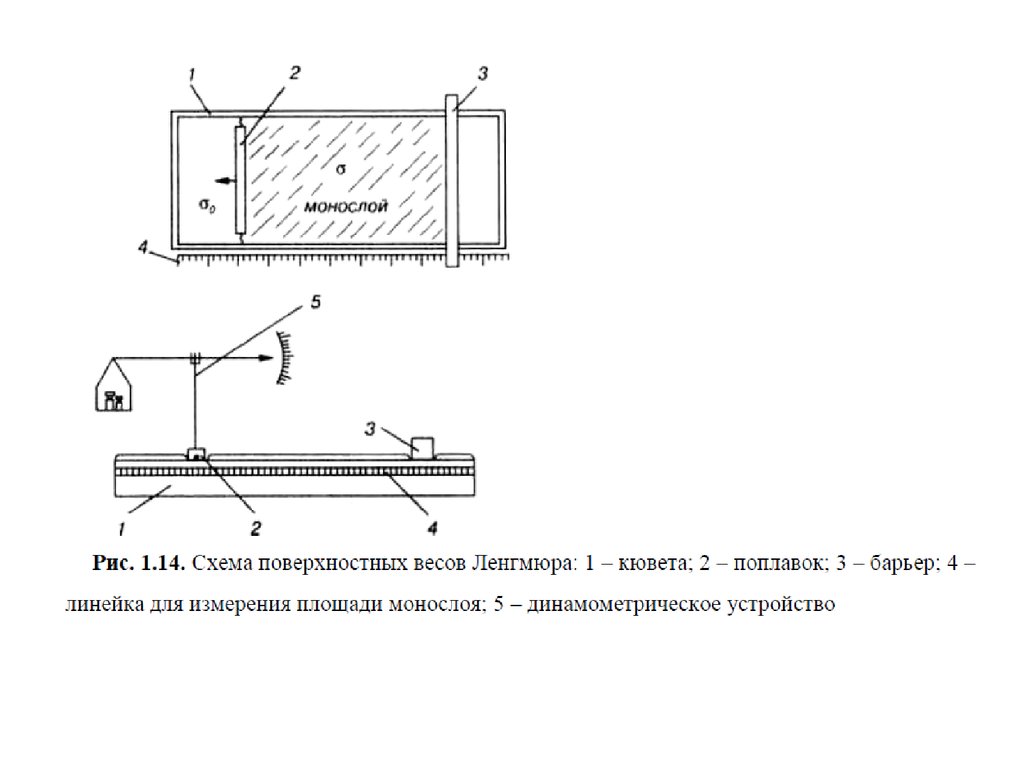
28. Весы Ленгмюра
29.
30.
31.
32.
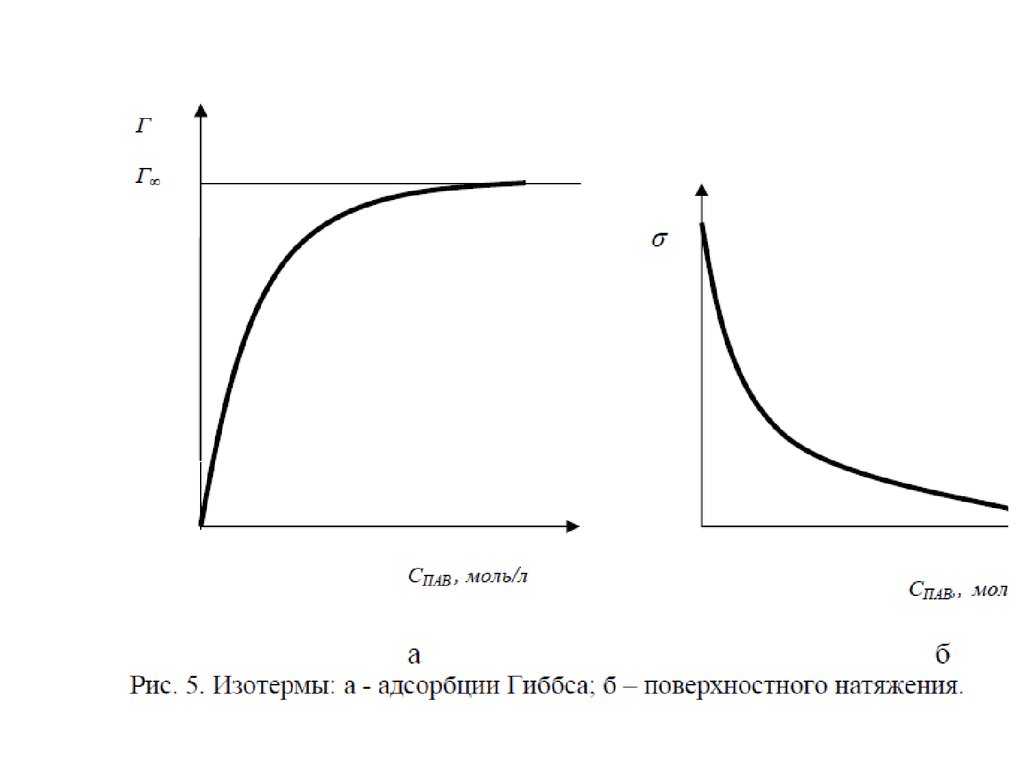
При адсорбции или растекании вещества на поверхности образуетсяповерхностная (адсорбционная) пленка этого вещества. Уравнение изотермы
поверхностного натяжения для ПАВ позволяют перейти к состояния
поверхностных пленок.
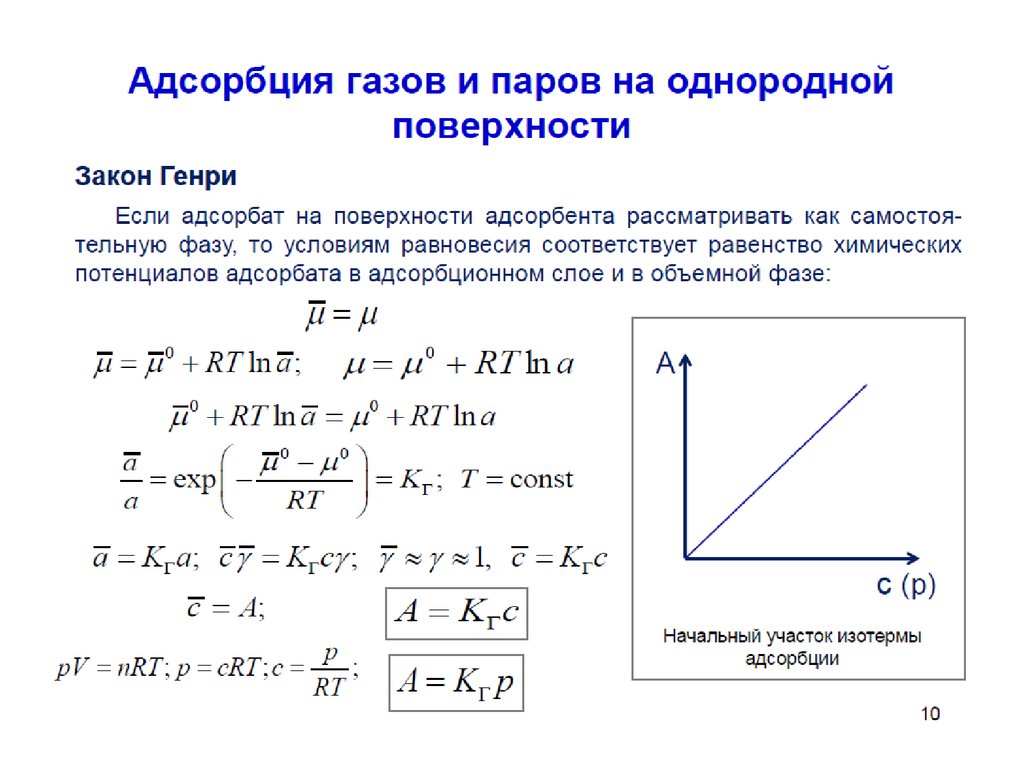
При очень малых концентрациях ПАВ распределение вещества
между раствором и поверхностным слоем описывается законом Генри
A kГ с
Подставив это выражение в уравнение Гиббса получим:
c d
kГ с
RT dc
После разделения переменных и интегрирования:
d
9
c
k Г RTdc
0
0 ART
33.
Введем обозначения:0
sm RT
1
sm
A
или если разделить на число Авогадро
kT
площадь приходящаяся в поверхностном слое на одну молекулу
адсорбата
Полученные выражение аналогичны уравнению состояния идеального газа
PVm RT
34.
В ряде случаев можно применять уравнение аналогичное уравнениюВан-дер-Ваальса
a
2 b kT
В котором константа
а
характеризует силы взаимного притяжения
адсорбат – адсорбат, а константа b площадь приходящуюся на молекулу
адсорбата в плотном монослое
35.
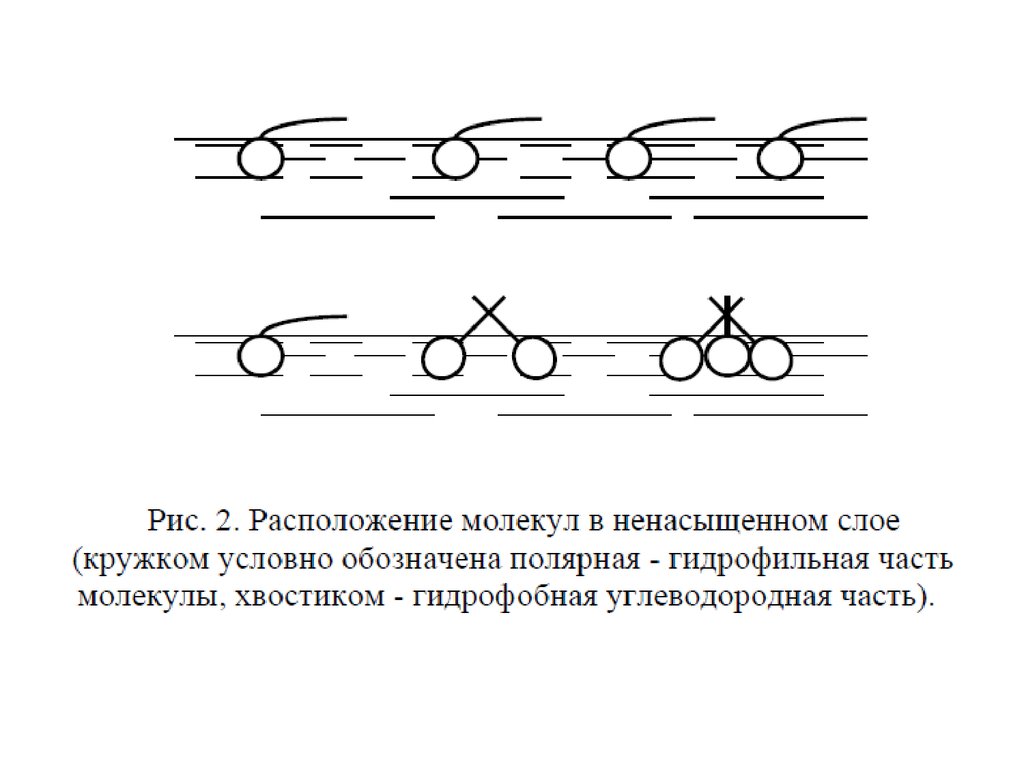
При небольшой концентрации амфифильногосоединения мономолекулярный слой на поверхности
не является сплошным. Молекулы практически не
взаимодействуют друг с другом, их хвосты над
поверхностью воды ориентированы произвольно, и
такую фазу по аналогии с обычной газообразной фазой
можно считать двумерным газом.
36.
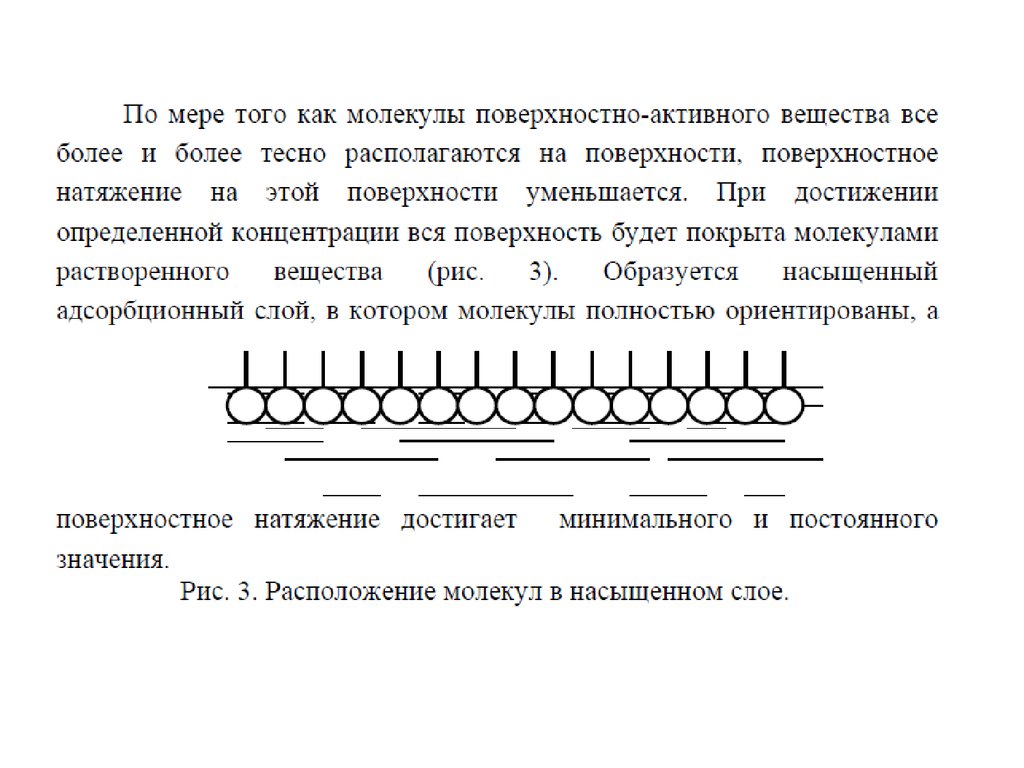
При уменьшении площади с помощьюплавучего барьера молекулы сблизятся, но будут
все еще хаотически ориентированы. Такую фазу
можно назвать двумерной жидкостью.
При дальнейшем уменьшении площади
дифильные молекулы приобретут
ориентационную упорядоченность, сохраняя
возможность перемещения в плоскости слоя.
При этом дальнего позиционного порядка не
существует, и новая фаза является двумерным
жидким кристаллом.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48. Изотерма адсорбции Лэнгмюра
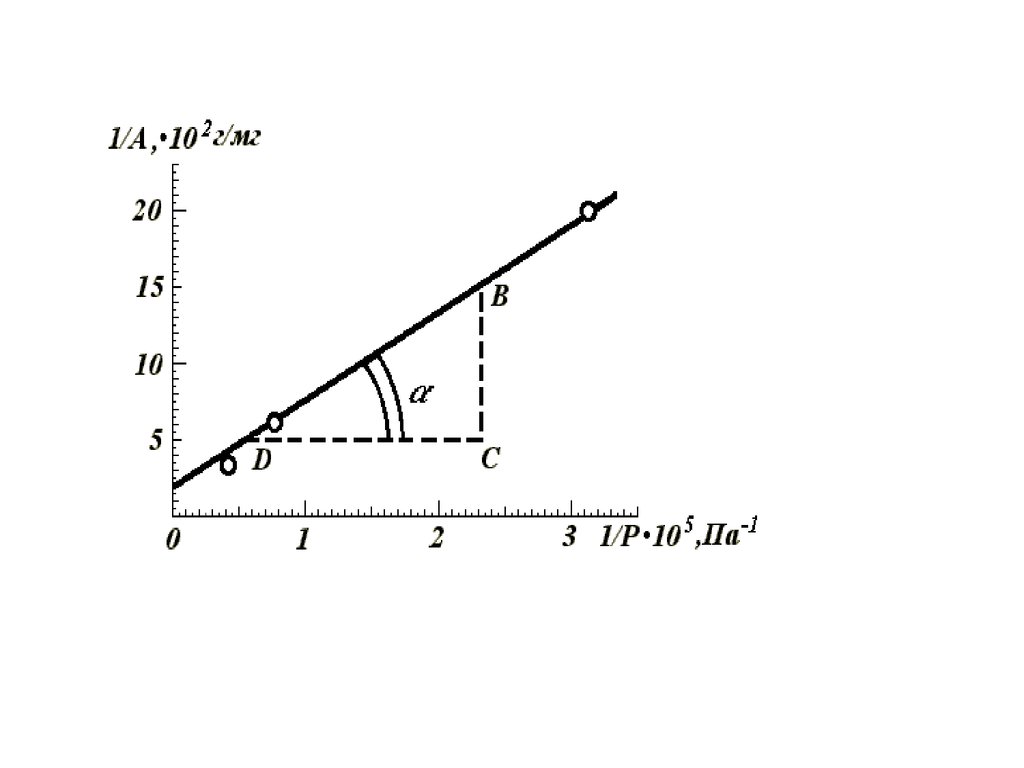
½Г∞49. Уравнение Ленгмюра в линейной форме
50.
51.
52.
53.
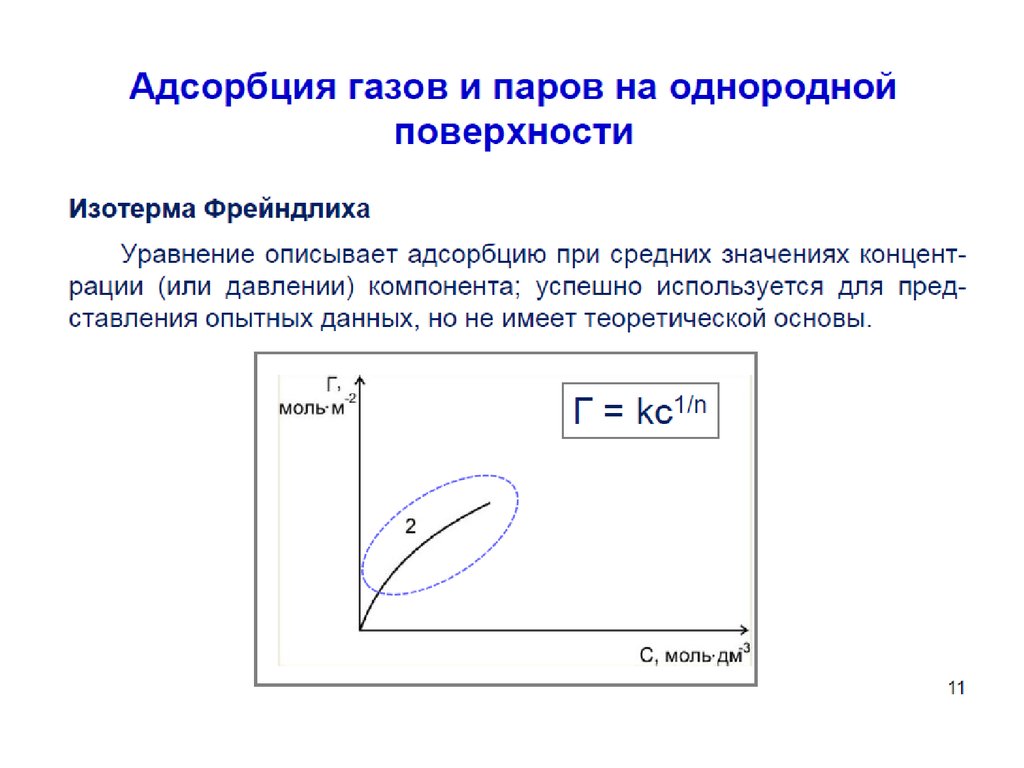
54. Уравнение Фрейндлиха.
Г K C1
n
К, 1/n – эмпирические постоянные,
т.е. на основе экспериментальных данных;
С – равновесная концентрация вещества, моль/дм3;
55.
56.
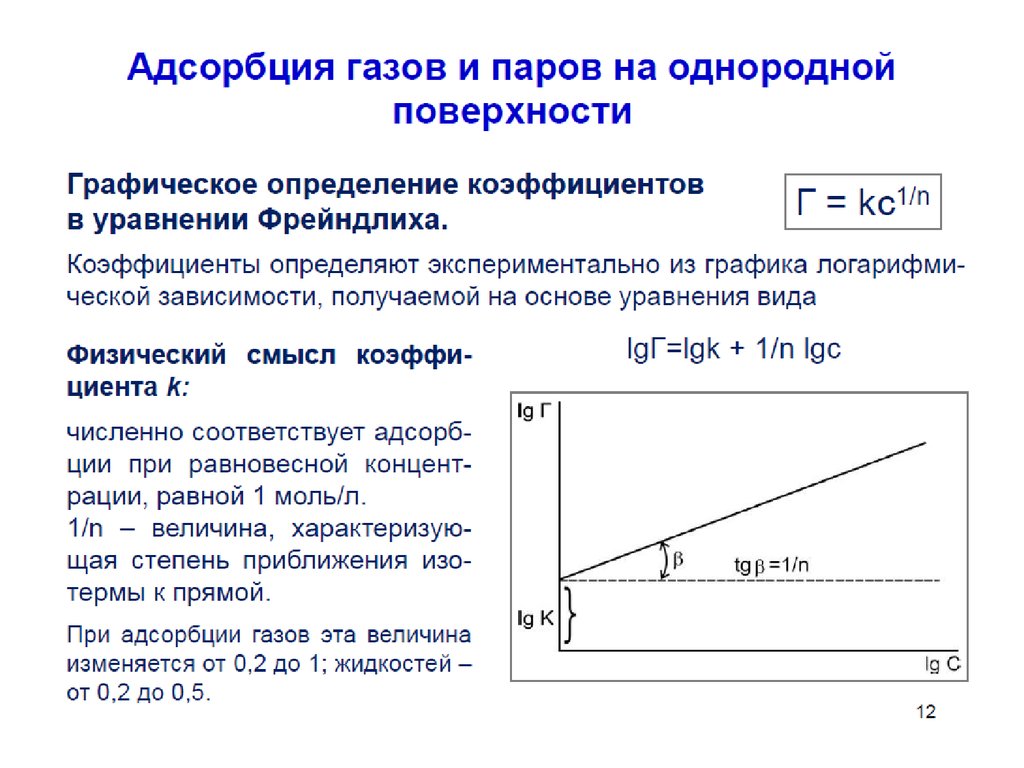
57. Уравнение Фрейндлиха.
Г K C1
n
К, 1/n – эмпирические постоянные,
т.е. на основе экспериментальных данных;
С – равновесная концентрация вещества, моль/дм3;
58.
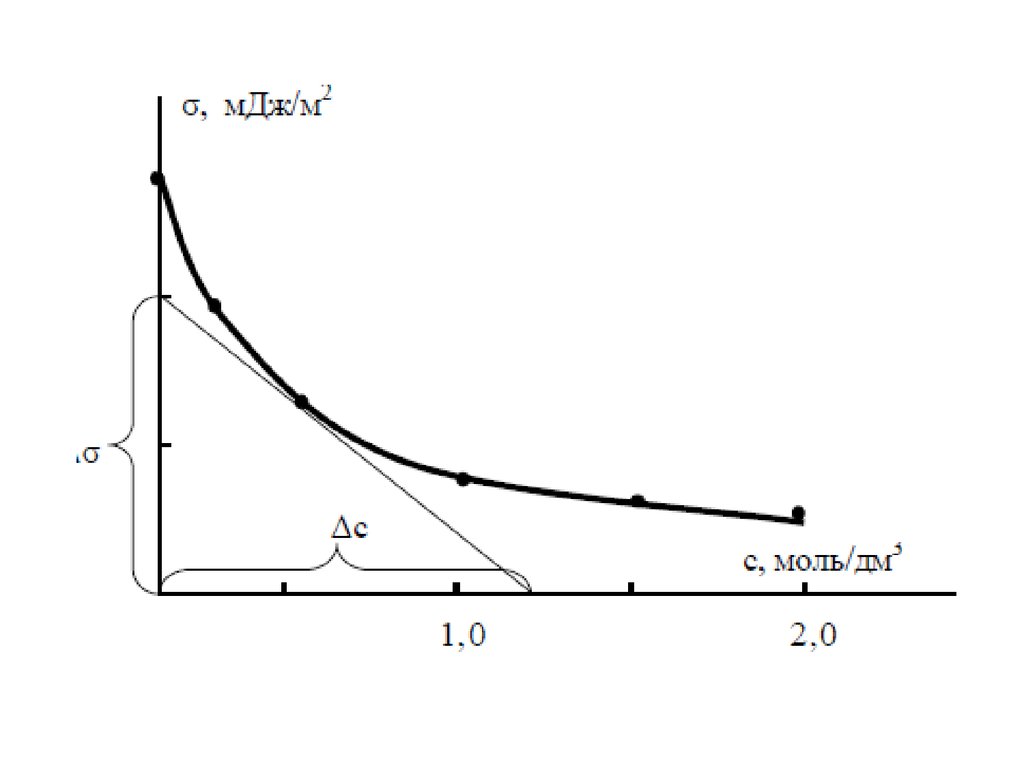
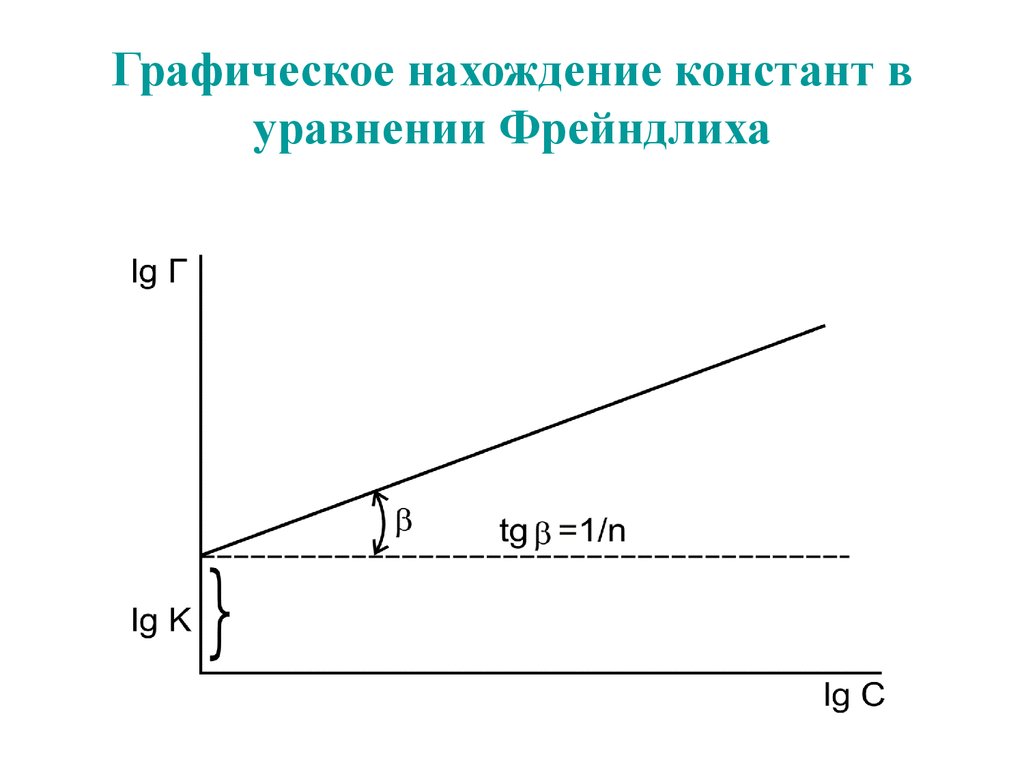
59. Графическое нахождение констант в уравнении Фрейндлиха
60.
61.
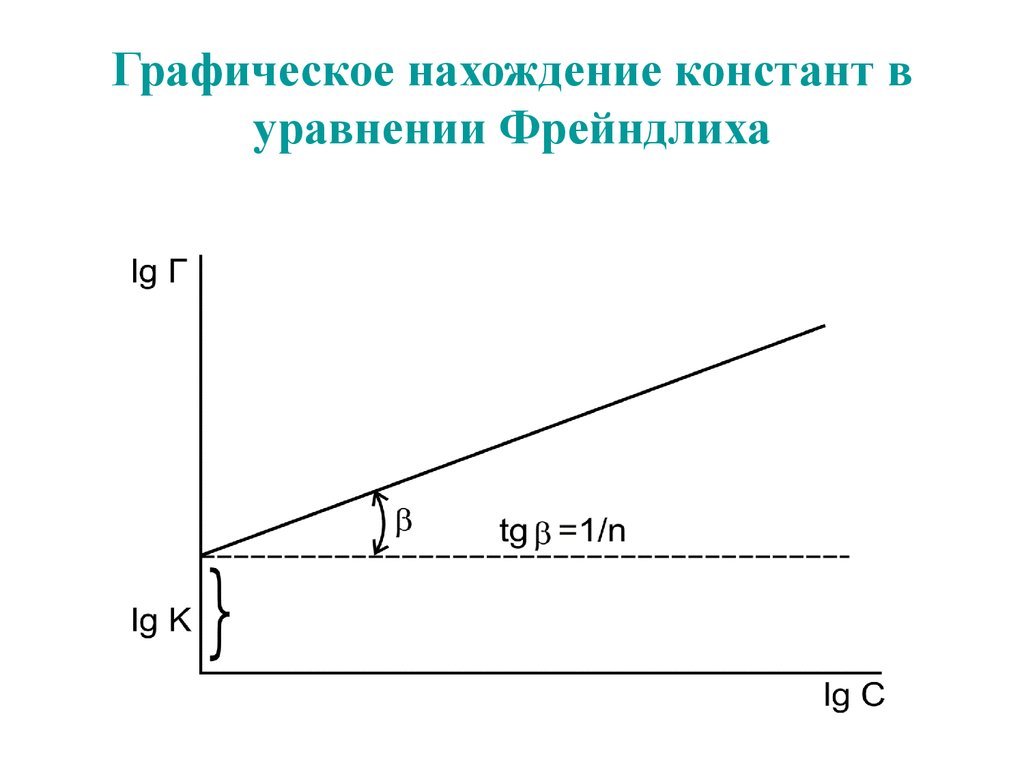
62. Графическое нахождение констант в уравнении Фрейндлиха
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
74.
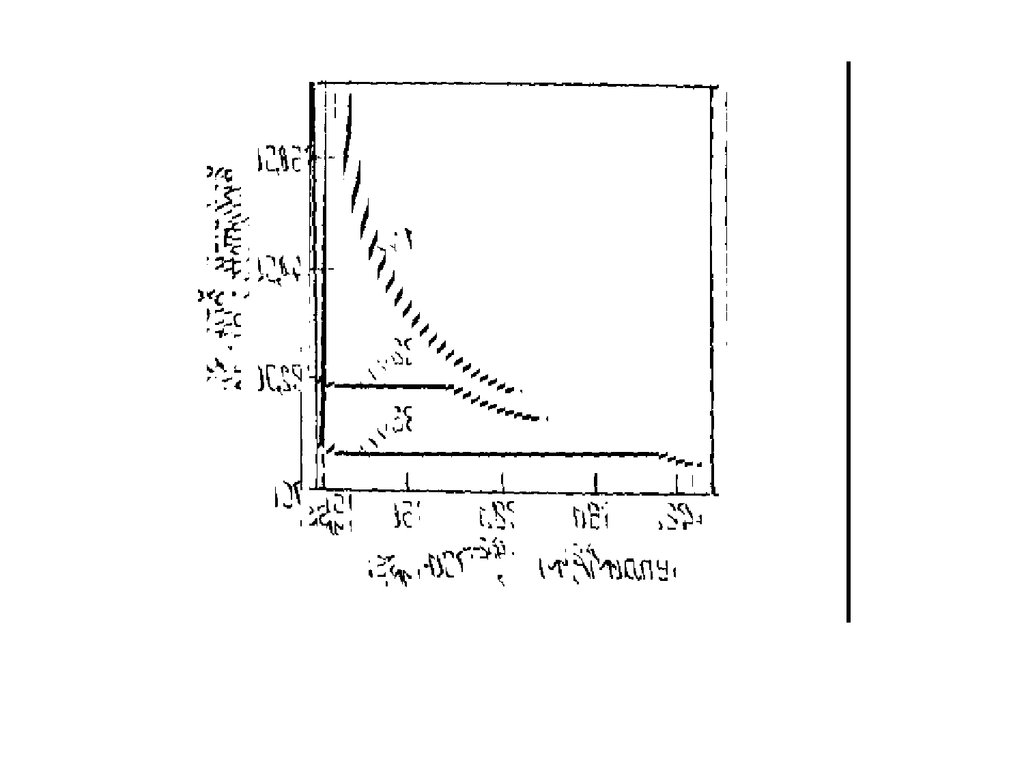
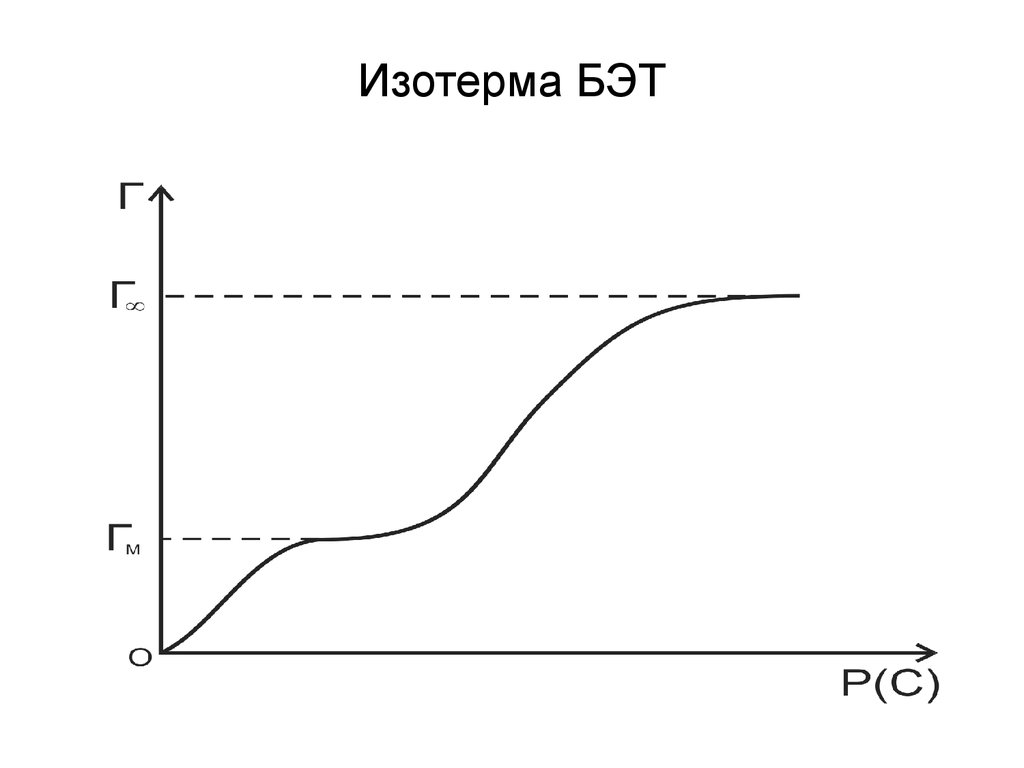
75. Изотерма БЭТ
76.
77.
С уменьшением давления уравнениеБЭТ переходит в уравнение мономолекулярной
адсорбции Ленгмюра.
При
P PS
A
A C P / Ps
1 C P / Ps



























































 chemistry
chemistry








