Similar presentations:
Теория графов в информатике
1. Теория графов в информатике
Теория графов в информатикеИсследовательская работа
2. Содержание
ВведениеТеория графов
Классические задачи
Графы в информатике
Заключение
3. Введение
4.
Графы используют во всех отраслях нашейжизни. Знание основ теории графов
необходимо в управлении производством,
бизнесе, при построении путей
транспортировки и доставки, решении
задач.
Графы используют в связи с развитием
теории вероятностей, математической
логики и информационных технологий.
5. Теория графов
Теория графов6.
Граф – это некоторое конечноемножество точек, называемых вершинами,
и конечный набор линий, называемых
ребрами, соединяющих некоторые пары
точек.
В
D
А
С
E
7. Понятия теории графов
Понятия теории графовСтепень вершины - число рёбер, выходящих
из этой вершины.
Граф называется взвешенным, если каждому
ребру поставлено в соответствии некоторое
число (вес).
Ориентированным (орграфом) называется
граф, у которого рёбрам присвоено
направление.
Плоский граф – граф, расположенный в одной
плоскости, ребра которого не пересекаются.
Полный граф – граф, в котором соединены все
вершины всеми возможными способами.
8. Некоторые свойства графов
Некоторые свойства графовЕсли все вершины графа чётные,
то можно одним росчерком
начертить граф.
Граф с двумя нечётными
вершинами тоже можно
начертить одним росчерком.
Граф с более чем двумя
нечётными вершинами,
невозможно начертить одним
росчерком.
9. Некоторые свойства плоских графов
Некоторые свойства плоских графовЛемма1. Число рёбер в графе ровно в 2
раза меньше, чем сумма степеней вершин.
Лемма2. Сумма степеней вершин графа
чётна.
Лемма3. Число нечётных вершин графа
чётно.
Лемма4. Если полный граф имеет n
вершин, то количество ребер будет равно
10. Классические задачи
Классические задачи11. «Жадные алгоритмы»
«Жадные алгоритмы»Требуется проложить железную дорогу,
соединяющую несколько городов. Для
любой пары городов известна стоимость
прокладки пути между ними. Требуется
найти наиболее дешёвый вариант
строительства. A B C D E
A
1.5
B
1.5
C
1
1.2
D
2
3
E
1
2
2.5
1.2
3
0.8
1.1 09
1.1
2.5 0.8 0.9 2.7
2.7
12. «Жадные алгоритмы»
«Жадные алгоритмы»A
B
C
E
D
13. Графы в информатике
Графы в информатике14. Блок-схемы
БлоксхемыЗадача:
Решение:
построить
попадания
Пусть Х0,Y0блок-схему
–центр поля
дротика
в цель в красного
игре «Дартс»
R и R – радиусы
и
1
черного полей
X и Y – это координаты стрелы
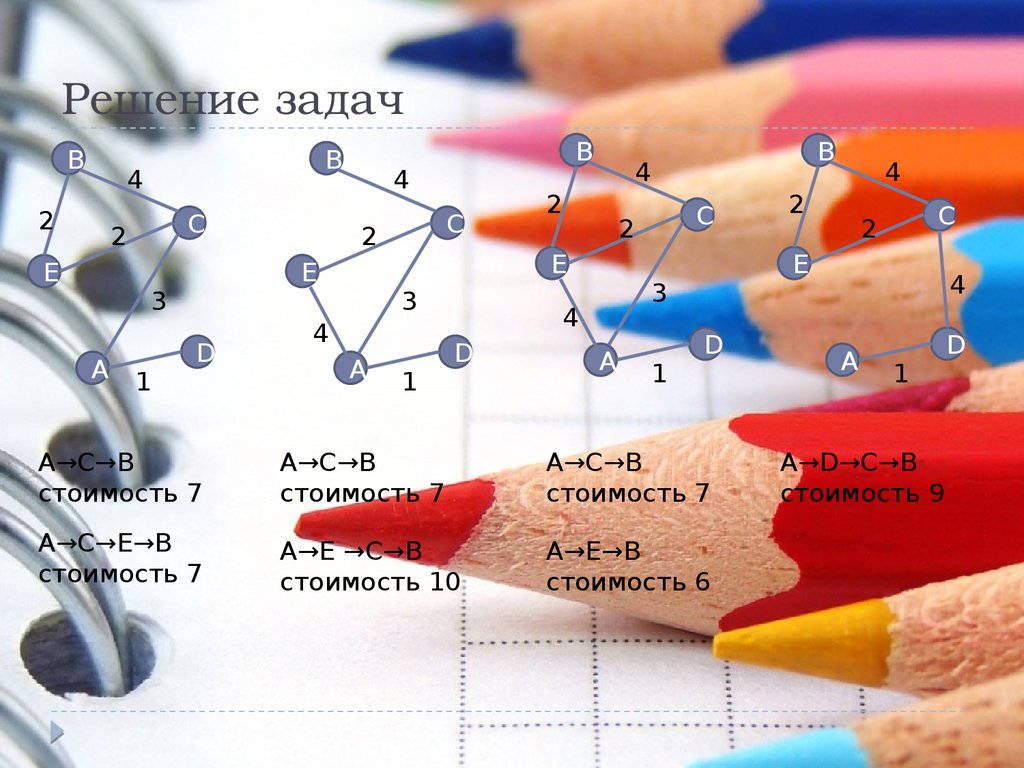
15. Решение задач
Решение задачНеобходимо указать таблицу, для которой
выполняется условие: «Минимальная
стоимость прокладки линии от клиента А до
клиента B не больше 6 у.е.».
A
C
D
A
3
1
B
4
C
3
D
1
E
B
4
E
A
C
D
E
A
3
1
4
2
B
4
2
C
3
A
2
2
B
A
C
D
E D
1
3
1
1 E
4
4
B
C
3
D
1
E
1
4
2
2
A
2
2
C
4
4
C
E
D
E
1
A
D
2
B
B
2
4
B
1
4
4
1
1
2
2
16. Решение задач
Решение задачA B C D E
A
3
B
4
C
3
D
1
E
2
B
A
1
4
A B C D E
3
2
B
2
C
3
D
1
E
4
2
2
4
2
B
C
2
E
A
1
4
D
C
2
E
3
4
4
4
2
1
A
3
B
4
C
3
D
1
E
4
4
1
A B C D E
4
A
2
B
2
C
D
2
B
1
4
1
E
2
2
C
2
1
4
D
2
4
B
2
2
4
2
C
2
E
3
A
2
4
4
4
D
1
4
E
3
A
A B C D E
4
A
1
D
17. Решение задач
Решение задачB
B
4
2
C
2
E
A
1
4
D
C
2
E
3
B
4
A
2
1
A
1
4
2
C
2
E
3
4
D
C
2
E
3
B
4
D
A→C→B
стоимость 7
A→C→B
стоимость 7
A→C→B
стоимость 7
A→C→E→B
стоимость 7
A→E →C→B
стоимость 10
A→E→B
стоимость 6
4
A
1
A→D→C→B
стоимость 9
D
18. Заключение
19.
На языке теории графов формируются ирешаются многие технические задачи,
задачи из области экономики, социологии,
менеджмента и многие другие.
Графы используются для наглядного
представления объектов и связи между
ними.
Но к теории графов также относится
целый ряд проблем, не решенных на
сегодняшний день.


















 informatics
informatics