Similar presentations:
Сопряжения линий в геометрических построениях
1. Сопряжения линий
2. Сопряжения линий
• Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжениядугой заданного радиуса нужно найти:
Центр сопряжения – центр, из которого проводят дугу;
Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.
3. Внешнее касание
• Расстояние между их центрами ОО1 равно сумме радиусов окружностей R+R14. Внутреннее касание
• Расстояние между их центрами ОО1 равно разности их радиусовR-R1
5. Сопряжение двух пересекающихся прямых
• Даны пересекающиеся под прямым, острым и тупым углами прямые линии.• Требуется построить сопряжения этих прямых дугой заданного радиуса R.
6. Сопряжение двух пересекающихся прямых
7. Сопряжение дуги окружности и прямой линии дугой заданного радиуса
Сопряжение дуги окружности ипрямой линии дугой заданного
радиуса
Дана окружность радиуса R и прямая АВ. Требуется
соединить их дугой радиусом R1.
8. Внешнее касание
Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.
1. Для нахождения центра сопряжения из центра О заданной
окружности проводят дугу m радиуса R + R1 и на расстоянии
R1 – прямую n // AB. Точка О1 пересечения прямой n и
дуги m будет центром сопряжения.
2. Для получения точек сопряжения: К и К1 проводят линию
центров ОО1 и восстанавливают к прямой АВ
перпендикуляр ОК1.
3. Из центра сопряжения О1 между точками К и К1 проводят
дугу сопряжения радиусом R1
9. Внутреннее касание
Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.
1. Для нахождения центра сопряжения из центра О заданной
окружности проводят дугу m радиуса R - R1и на расстоянии
R1 – прямую n // AB. Точка О1 пересечения прямой n и
дуги m будет центром сопряжения.
2. Для получения точек сопряжения: К и К1 проводят линию
центров ОО1 и восстанавливают к прямой АВ
перпендикуляр ОК1.
3. Из центра сопряжения О1 между точками К и К1 проводят
дугу сопряжения радиусом R1
10. Сопряжение двух окружностей дугой заданного радиуса
Заданы две окружности радиусом R1 и R2. Требуется построитьсопряжение дугой заданного радиуса R
11. Внешнее касание
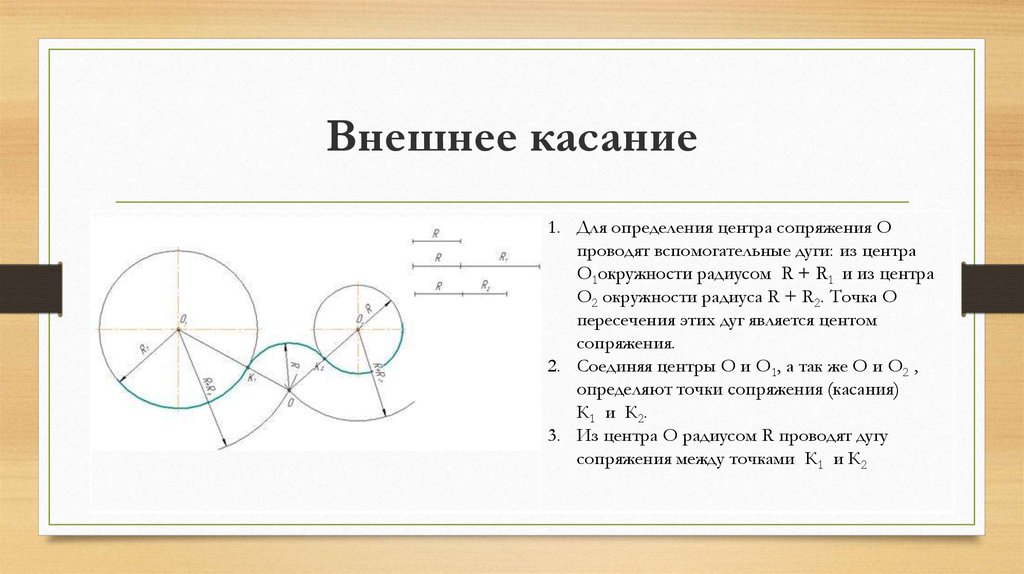
1. Для определения центра сопряжения Опроводят вспомогательные дуги: из центра
О1окружности радиусом R + R1 и из центра
О2 окружности радиуса R + R2. Точка О
пересечения этих дуг является центом
сопряжения.
2. Соединяя центры О и О1, а так же О и О2 ,
определяют точки сопряжения (касания)
К1 и К2.
3. Из центра О радиусом R проводят дугу
сопряжения между точками К1 и К2
12. Внутреннее касание
1. Для определения центра сопряжения Опроводят вспомогательные дуги: из центра
О1окружности радиусом R - R1 и из центра
О2 окружности радиуса R - R2. Точка О
пересечения этих дуг является центом
сопряжения.
2. Соединяя центры О и О1, а так же О и О2 ,
определяют точки сопряжения (касания)
К1 и К2.
3. Из центра О радиусом R проводят дугу
сопряжения между точками К1 и К2
13. Смешанное касание
1. Центр сопряжения О находится впересечении двух дуг, описанных из центра
О1 радиусом R - R1 и из центра О2 радиусом
R + R2
2. Соединяя центры О и О1, а так же О и О2 ,
определяют точки сопряжения (касания)
К1 и К2.
3. Из центра О радиусом R проводят дугу
сопряжения между точками К1 и К2
При смешанном сопряжении центр О1 одной из
сопрягаемых дуг лежит внутри сопрягающей дуги
радиуса R , а центр О2 другой дуги – вне ее.












 mathematics
mathematics drafting
drafting








