Теоремы к зачёту

1.

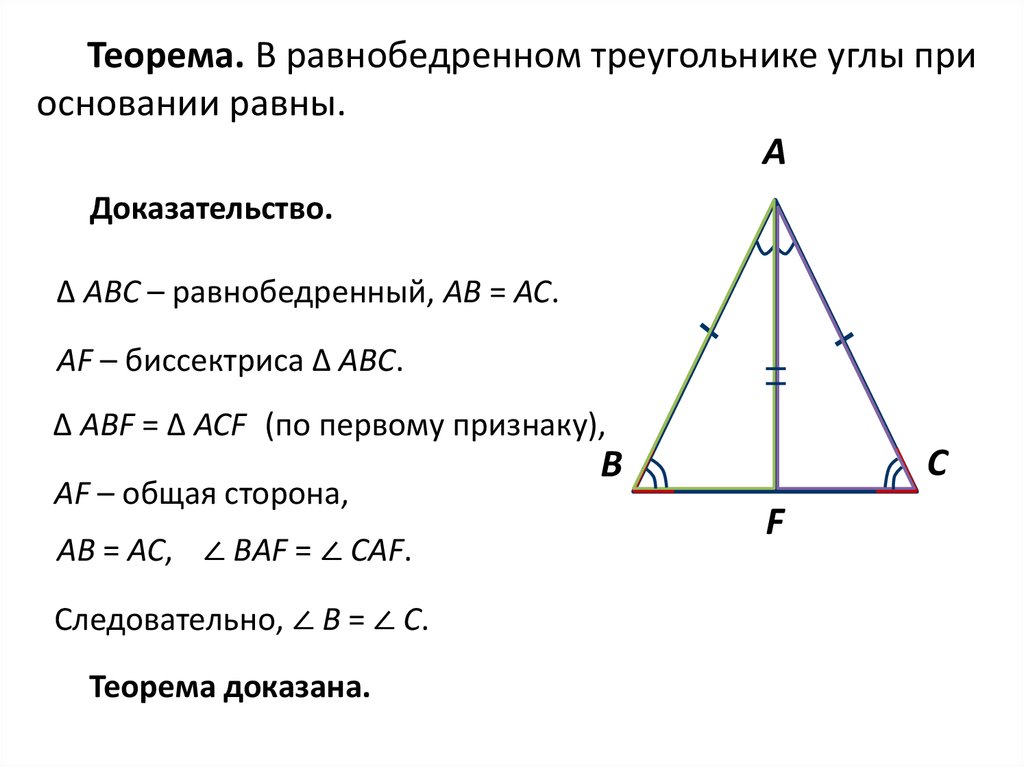
Теорема. В равнобедренном треугольнике углы при
основании равны.
А
Доказательство.
∆ АВС – равнобедренный, АВ = АС.
AF – биссектриса ∆ АВС.
∆ АВF = ∆ АСF (по первому признаку),
AF – общая сторона,
AВ = АС, ∠ ВAF = ∠ СAF.
Следовательно, ∠ В = ∠ С.
Теорема доказана.
С
В
F

2.

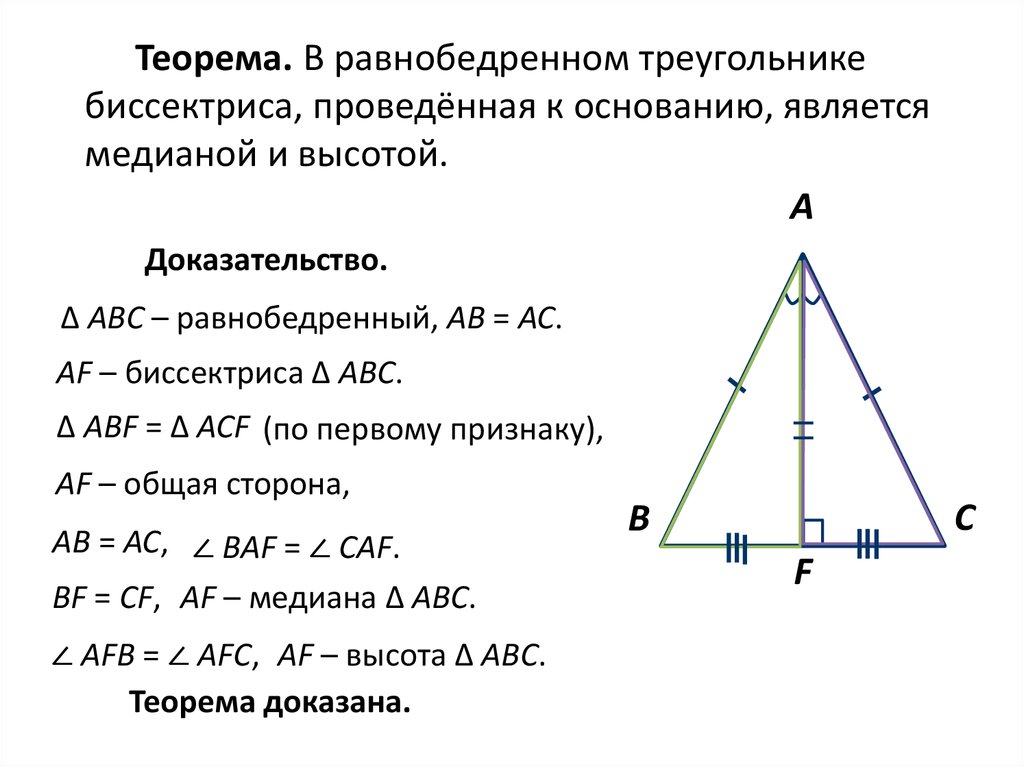
Теорема. В равнобедренном треугольнике
биссектриса, проведённая к основанию, является
медианой и высотой.
А
Доказательство.
∆ АВС – равнобедренный, АВ = АС.
AF – биссектриса ∆ АВС.
∆ АВF = ∆ АСF (по первому признаку),
AF – общая сторона,
AВ = АС, ∠ ВAF = ∠ СAF.
ВF = СF, AF – медиана ∆ АВС.
∠ AFВ = ∠ АFС, AF – высота ∆ АВС.
Теорема доказана.
С
В
F

3.

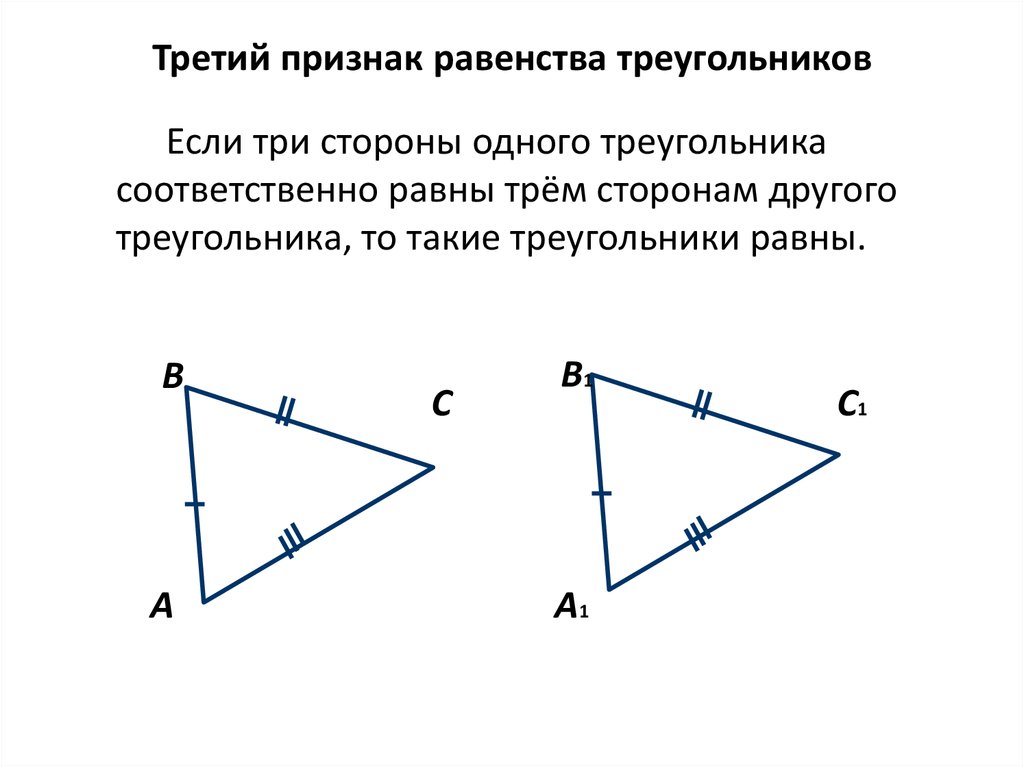
Третий признак равенства треугольников
Если три стороны одного треугольника
соответственно равны трём сторонам другого
треугольника, то такие треугольники равны.
В
А
С
В1
А1
С1

4.

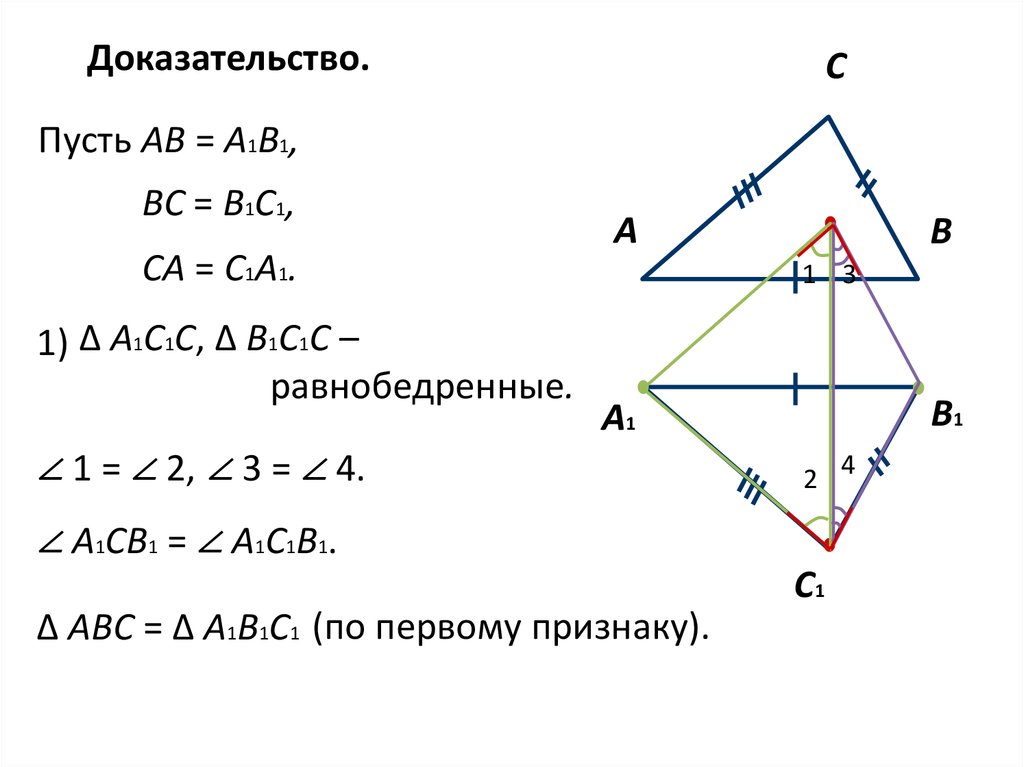
Доказательство.
С
Пусть АВ = А1В1,
ВС = В1С1,
СА = С1А1.
1) ∆ А1С1С, ∆ В1С1С –
равнобедренные.
А
В
1 3
В1
А1
∠ 1 = ∠ 2, ∠ 3 = ∠ 4.
2 4
∠ А1СВ1 = ∠ А1С1В1.
С1
∆ АВС = ∆ А1В1С1 (по первому признаку).

5.

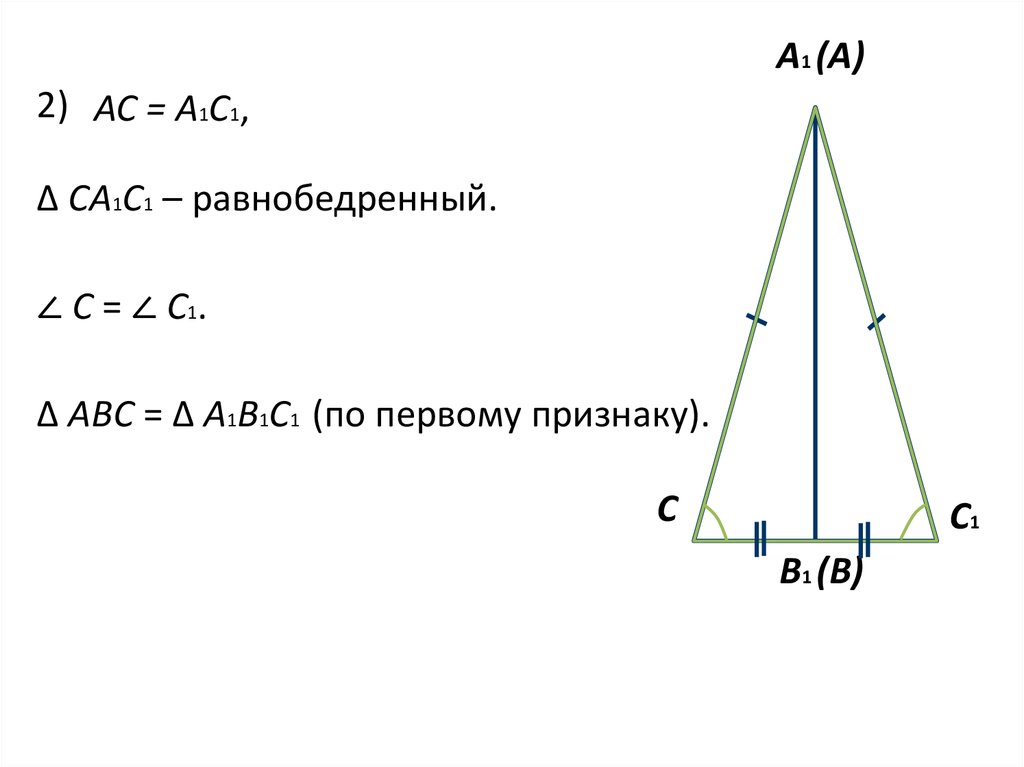
А1 (А)
2) АС = А1С1,
∆ СА1С1 – равнобедренный.
∠ С = ∠ С1.
∆ АВС = ∆ А1В1С1 (по первому признаку).
С
С1
В1 (В)

6.

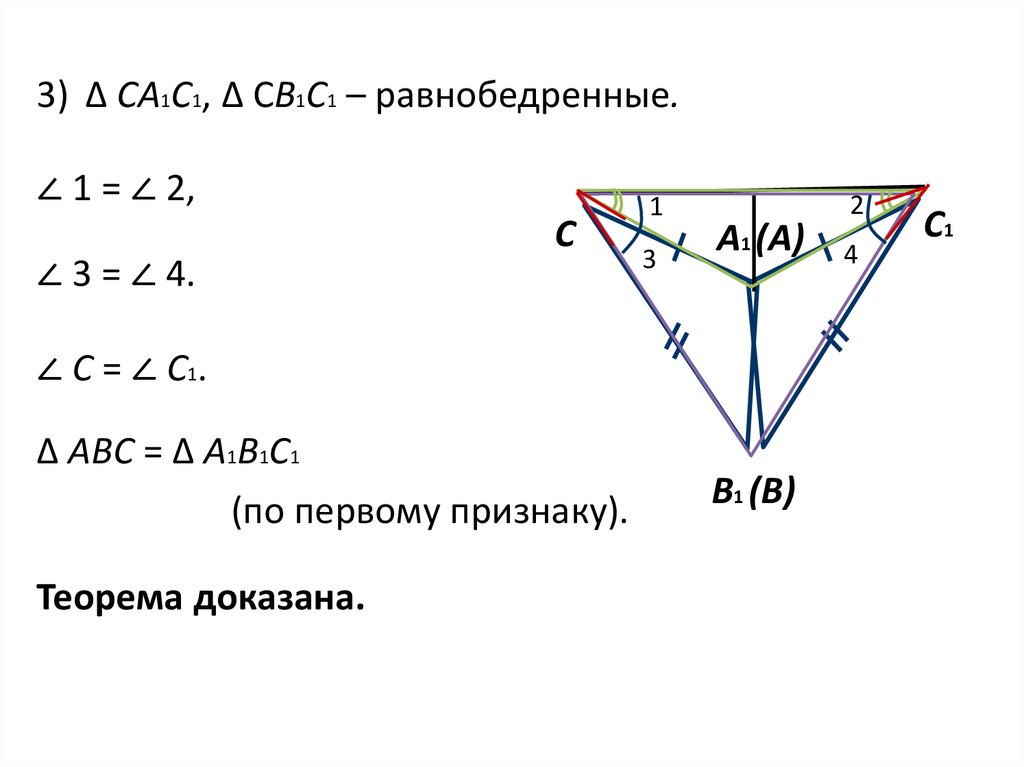
3) ∆ СА1С1, ∆ СВ1С1 – равнобедренные.
∠ 1 = ∠ 2,
С
∠ 3 = ∠ 4.
1
3
А1 (А)
∠ С = ∠ С1.
∆ АВС = ∆ А1В1С1
(по первому признаку).
Теорема доказана.
В1 (В)
2
4
С1