Similar presentations:
Простейшие задачи в координатах
1.
Урок геометрии в 9 классе2.
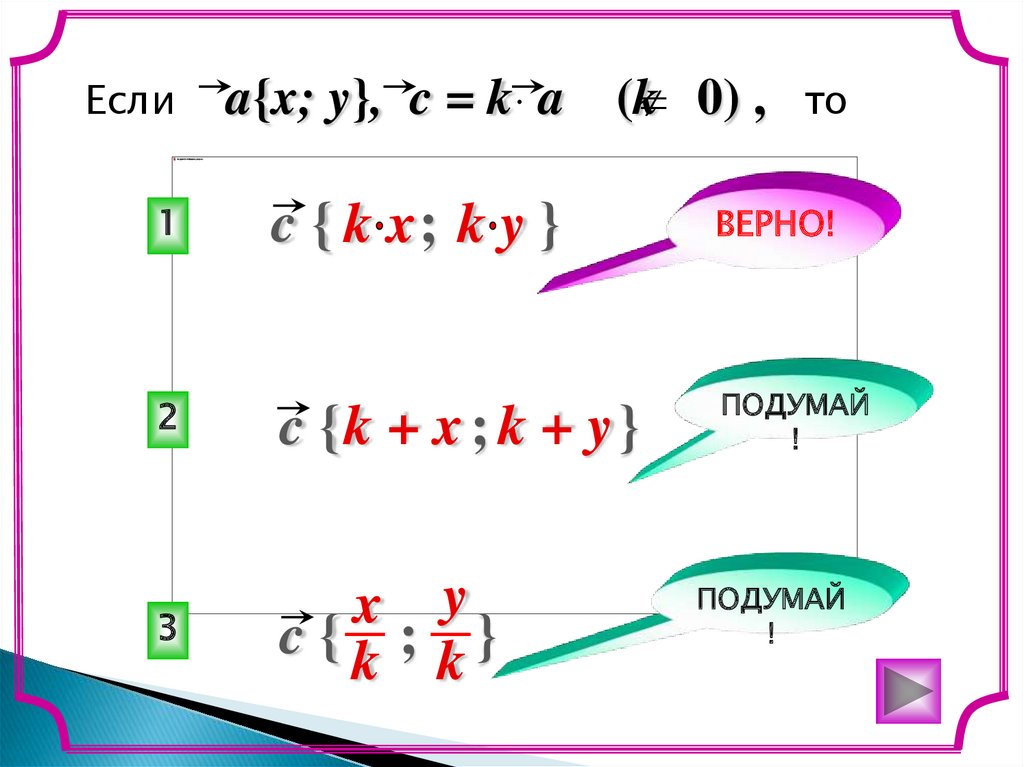
(k 0) ,Если
a{x; y}, c = k a
1
c { k x; k y }
ВЕРНО!
c {k + x ; k + y }
ПОДУМАЙ
!
2
3
x y
c {k ; k}
то
ПОДУМАЙ
!
3.
Еслиa{m; n}, b{p; k}, c = a + b,
то
ПОДУМАЙ
!
1
c { c p; n k }
ПОДУМАЙ
!
2
c {m + n; p + k }
ВЕРНО!
3
c {m + p ; n + k}
4.
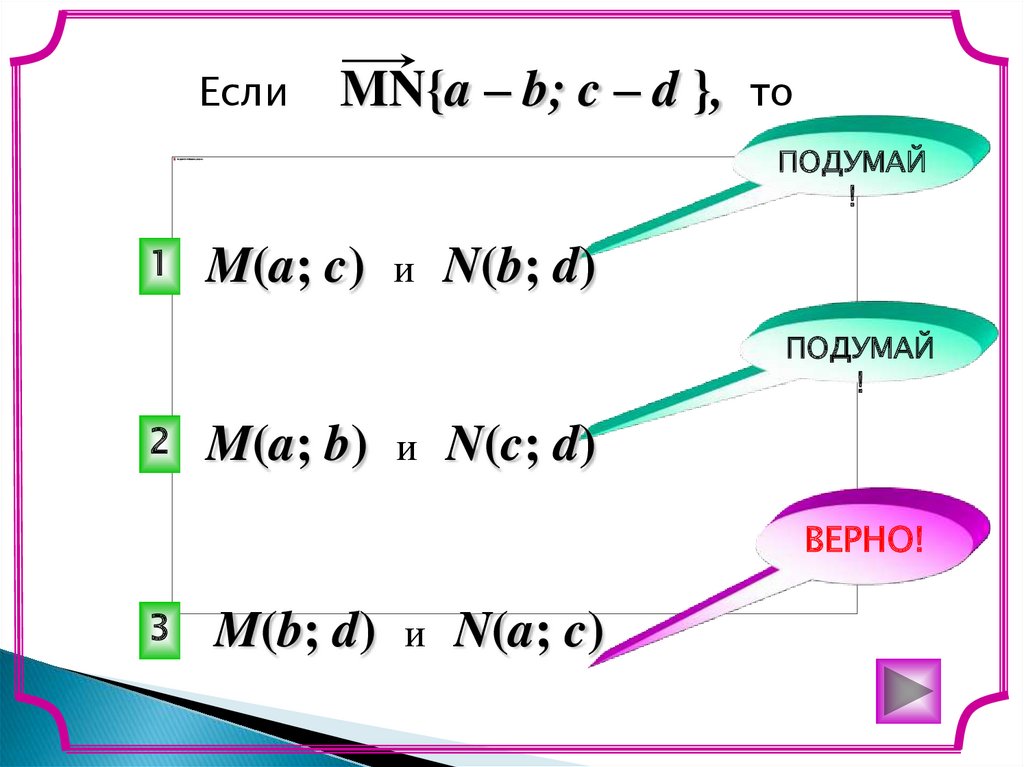
ЕслиMN{a – b; c – d },
то
ПОДУМАЙ
!
1
M(a; c)
и
N(b; d)
ПОДУМАЙ
!
2
M(a; b)
и
N(c; d)
ВЕРНО!
3
M(b; d)
и
N(a; c)
5.
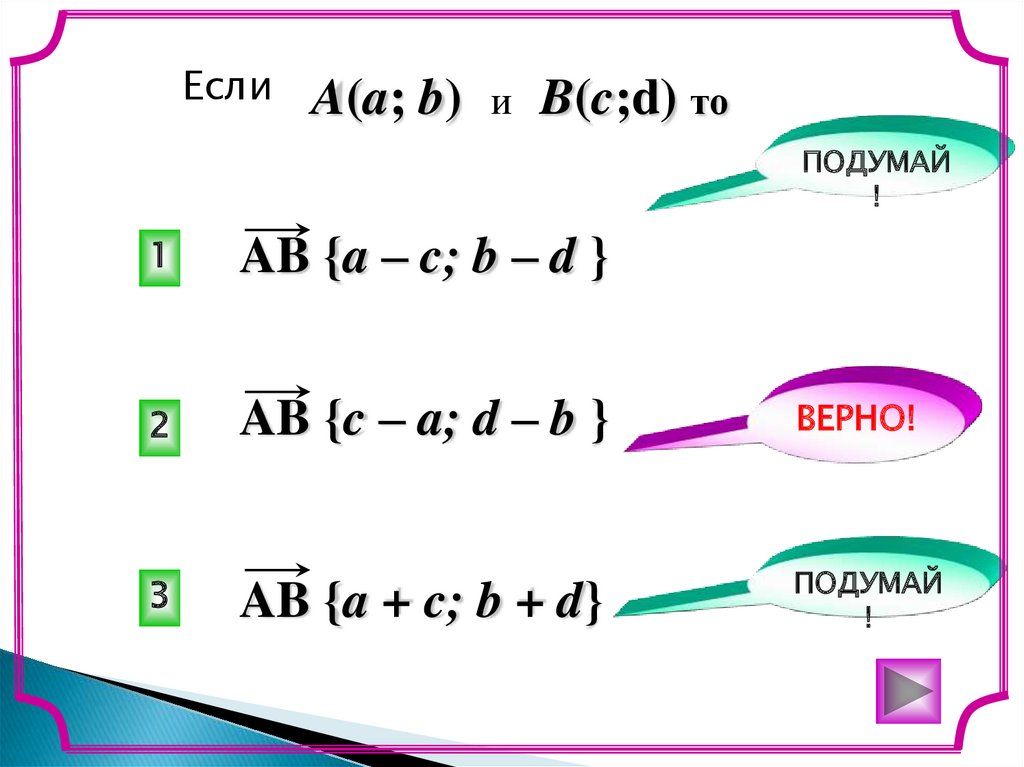
ЕслиA(a; b)
и
B(c;d) то
ПОДУМАЙ
!
1
AB {a – c; b – d }
2
AB {c – a; d – b }
ВЕРНО!
AB {a + c; b + d}
ПОДУМАЙ
!
3
6.
Найти координатывекторов.
R(2;7); M(-2;7); RM{
}
P(-5;1); D(-5;7); PD {
}
R(-3;0); N(0;5);
RN {
}
A(0;3); B(-4;0);
BA {
}
A(-2;7); B(-2;0); AB {
}
R(-7;7); T(-2;-7); RT {
}
7.
Координаты середины отрезкаOA{x1;y1}
+
1
ОС (ОА ОВ )
2
OB{x2;y2}
OA+OB {x1+x2; y1+y2}
y
B(x2;y2)
1
2
C (x0;y0)
:2
x1+x2 y1+y2
(OA+OB) { 2 ; 2 }
x1+x2 y1+y2
OC { 2 ; 2 }
A(x1;y1)
О
x
x0=
x1+x2
2
; y0 =
y1+y2
2
8.
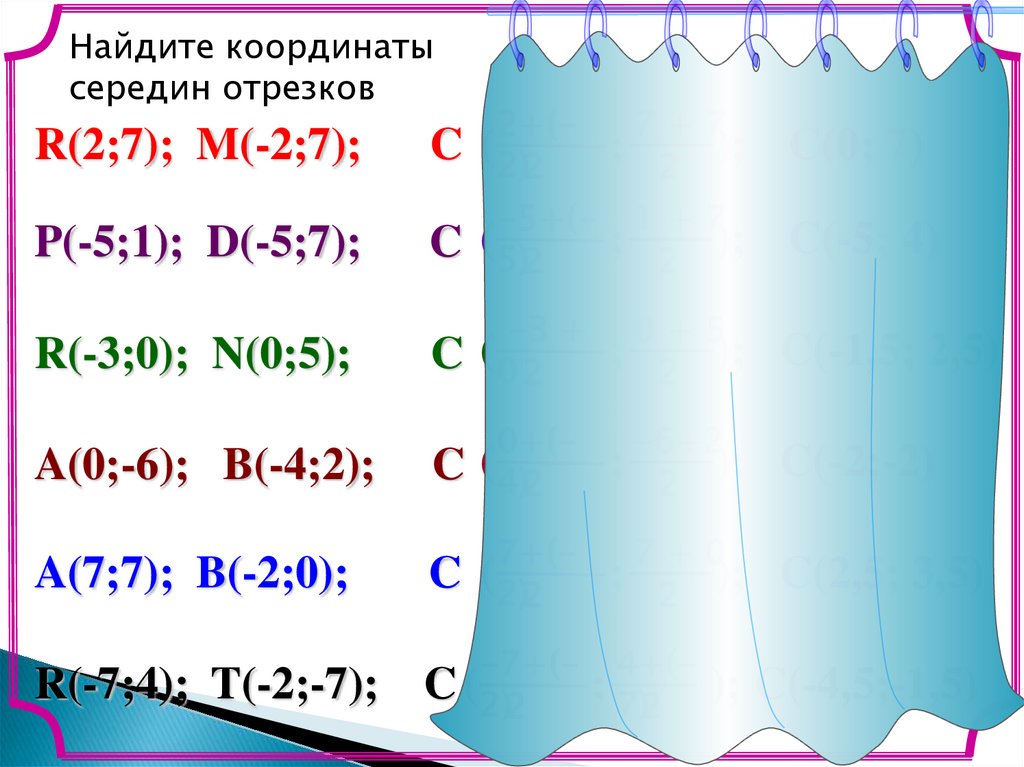
Найдите координатыcередин отрезков
C
2+(( 2)2
7+7
; 2 );
C(0; 7)
C
-5+(( 5)2
1+7
; 2 );
C(-5; 4)
C
-3 +
(0 2
0+5
; 2 );
C(-1,5; 2,5)
C
0+(( 4)2
-6+2
; 2 );
C(-2;-2)
A(7;7); B(-2;0);
C
7+(( 2)2
7+0
; 2 );
C(2,5; 3,5)
R(-7;4); T(-2;-7);
-7+(C ( 2)2
R(2;7); M(-2;7);
P(-5;1); D(-5;7);
R(-3;0); N(0;5);
A(0;-6); B(-4;2);
4+(; 7)2
); C(-4,5;-1,5)
9.
Найти координаты середин отрезков.R(2;7); M(-2;7);
C(
)
P(-5;1); D(-5;7);
C(
)
R(-3;0); N(0;5);
C(
)
A(0;-6); B(-4;2);
C(
)
A(7;7); B(-2;0);
C(
)
R(-7;4); T(-2;-7);
C(
)
10.
Вычисление длины вектора по его координатамOA2=OA12 + AA12
y
OA2= x2 + y2
OA
OA= a{x;y}
A (x;y)
A2
y
О
a
OA = x2 + y2
=
x
A1
x
=
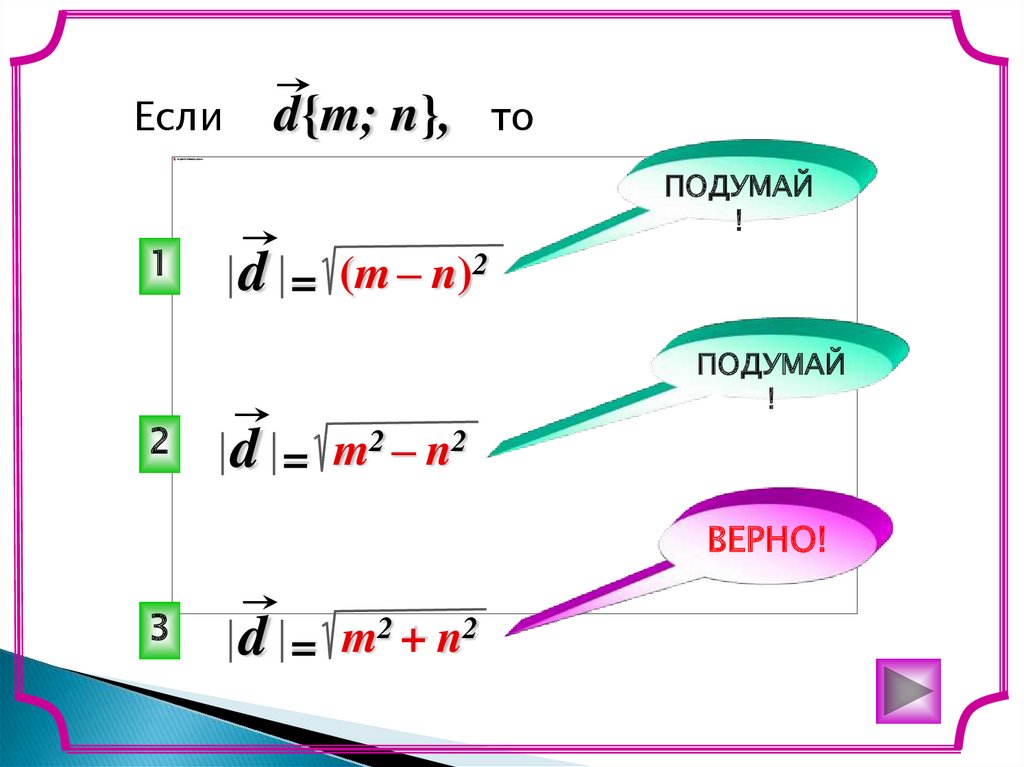
11.
Еслиd{m; n},
то
ПОДУМАЙ
!
1
d = (m – n)2
ПОДУМАЙ
!
2
d = m2 – n2
ВЕРНО!
3
d = m2 + n2
12.
Расстояние между двумя точкамиy
–
M2(x2;y2)
d
M2(x2;y2)
M1(x1;y1)
M1M2 {x2–x1; y2–y1}
M1(x1;y1)
O
x
a = x2 + y2
M1M2 = (x2–x1)2+(y2–y1)2
d = (x2–x1)2+(y2–y1)2
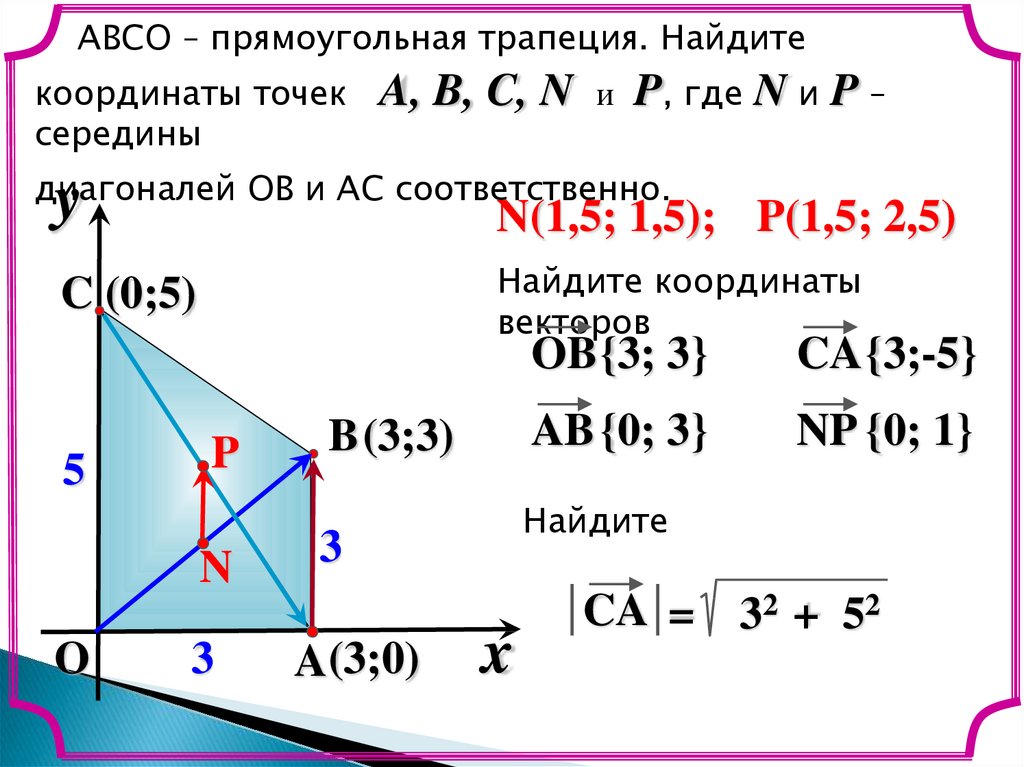
13.
ABCО – прямоугольная трапеция. Найдитекоординаты точек
середины
A, B, C, N
и
P, где N и P –
диагоналей OB и AC соответственно.
y
N(1,5; 1,5); P(1,5; 2,5)
C (0;5)
Найдите координаты
векторов
5
P
N
O
3
B (3;3)
CA {3;-5}
AB {0; 3}
NP {0; 1}
Найдите
3
A(3;0)
OB {3; 3}
x
CA =
32 + 52
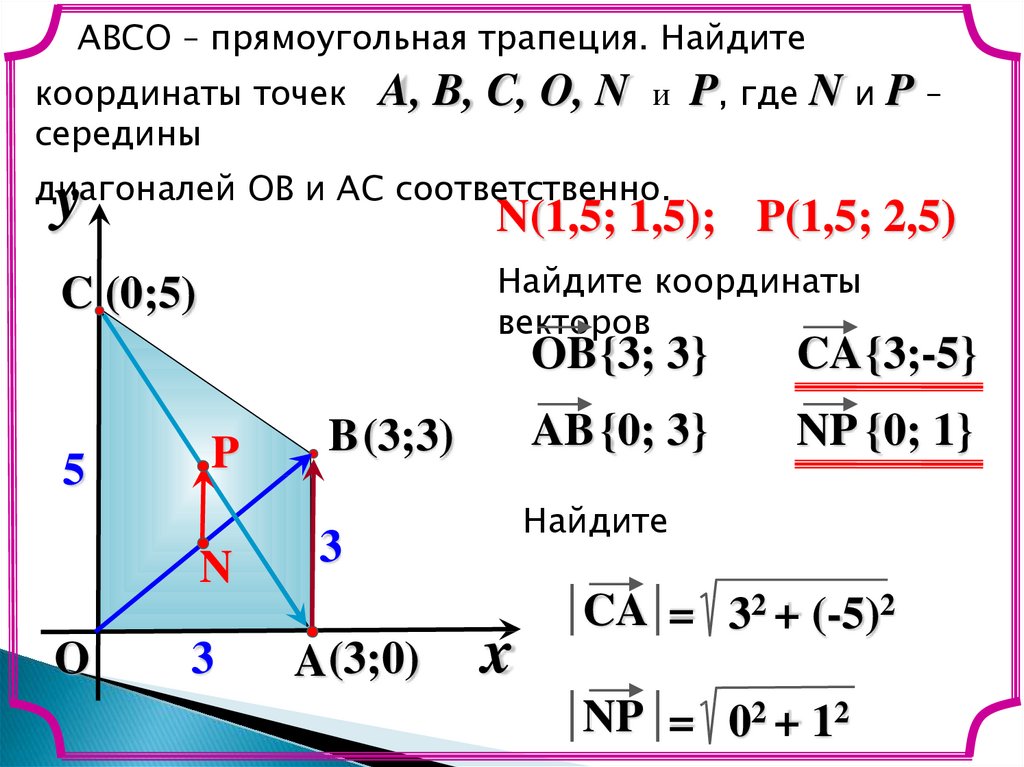
14.
ABCО – прямоугольная трапеция. Найдитекоординаты точек
середины
A, B, C, O, N
и
P, где N и P –
диагоналей OB и AC соответственно.
y
N(1,5; 1,5); P(1,5; 2,5)
C (0;5)
Найдите координаты
векторов
5
P
N
O
3
B (3;3)
CA {3;-5}
AB {0; 3}
NP {0; 1}
Найдите
3
A(3;0)
OB {3; 3}
x
CA = 32 + (-5)2
NP = 02 + 12
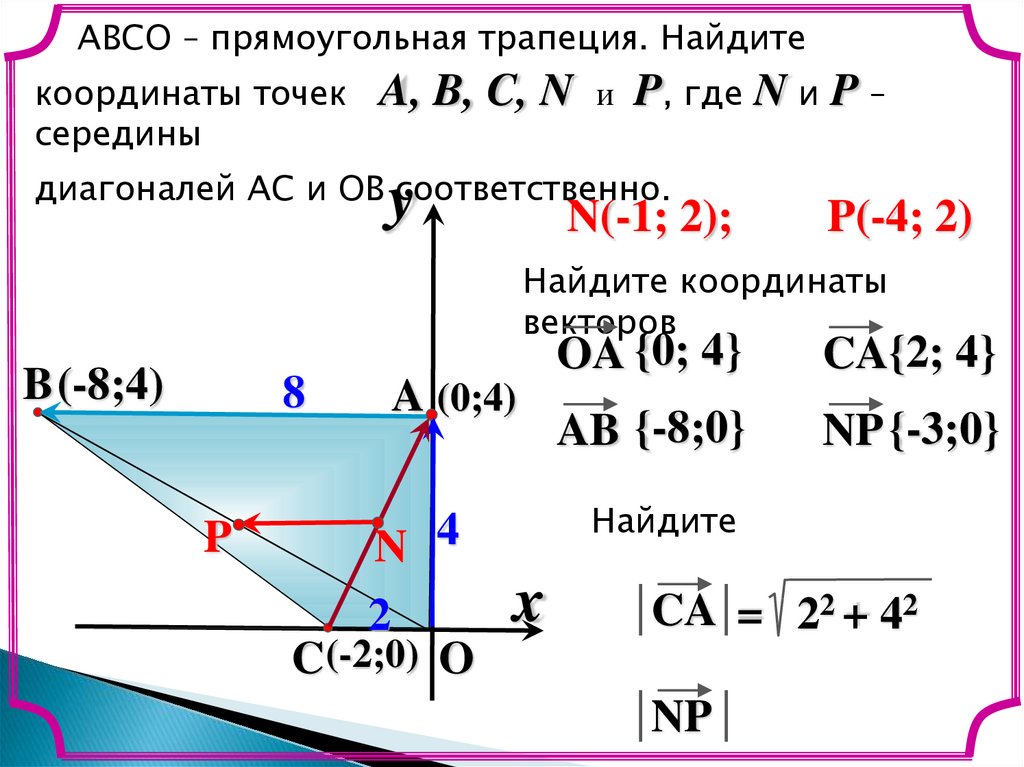
15.
ABCО – прямоугольная трапеция. Найдитекоординаты точек
середины
A, B, C, N
и
P, где N и P –
диагоналей AC и OB соответственно.
y
N(-1; 2);
P(-4; 2)
Найдите координаты
векторов
B (-8;4)
8
P
A (0;4)
N 4
2
C(-2;0) O
OA {0; 4}
CA{2; 4}
AB {-8;0}
NP {-3;0}
Найдите
x
CA = 22 + 42
NP
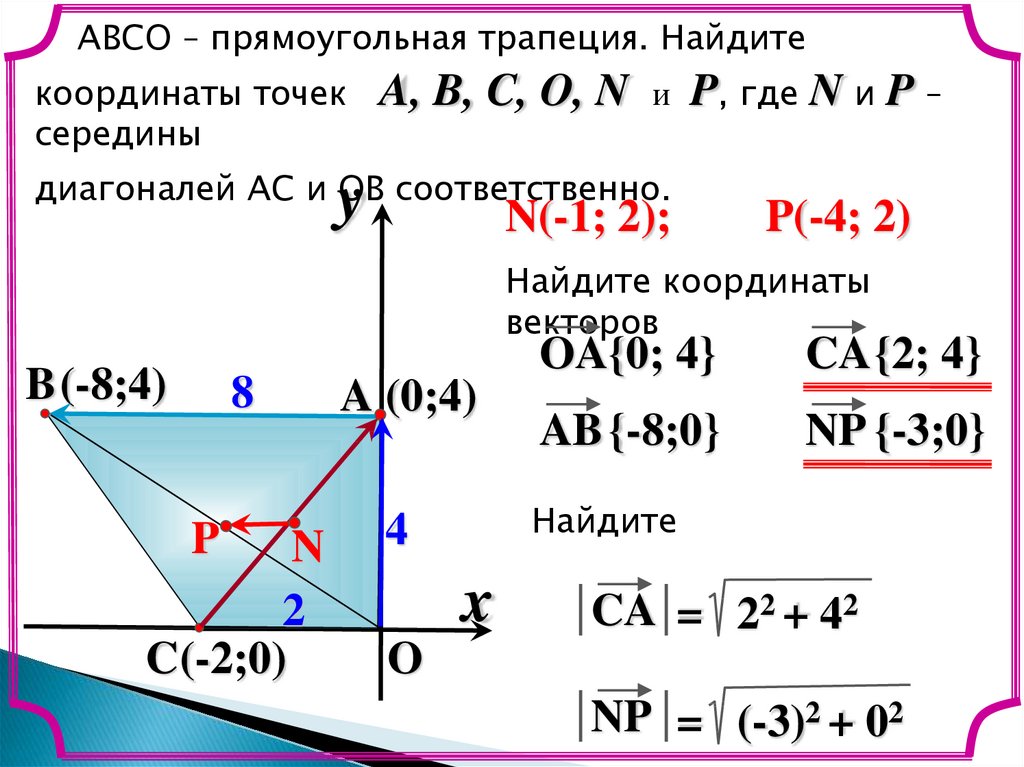
16.
ABCО – прямоугольная трапеция. Найдитекоординаты точек
середины
A, B, C, O, N
и
P, где N и P –
диагоналей AC и OB соответственно.
y
N(-1; 2);
P(-4; 2)
Найдите координаты
векторов
B (-8;4)
8
A (0;4)
N
2
C(-2;0)
4
P
OA{0; 4}
CA {2; 4}
AB {-8;0}
NP {-3;0}
Найдите
x
CA = 22 + 42
O
NP = (-3)2 + 02
17.
№942y
С (5;2)
A (0;1)
x
М
В (1;-4)
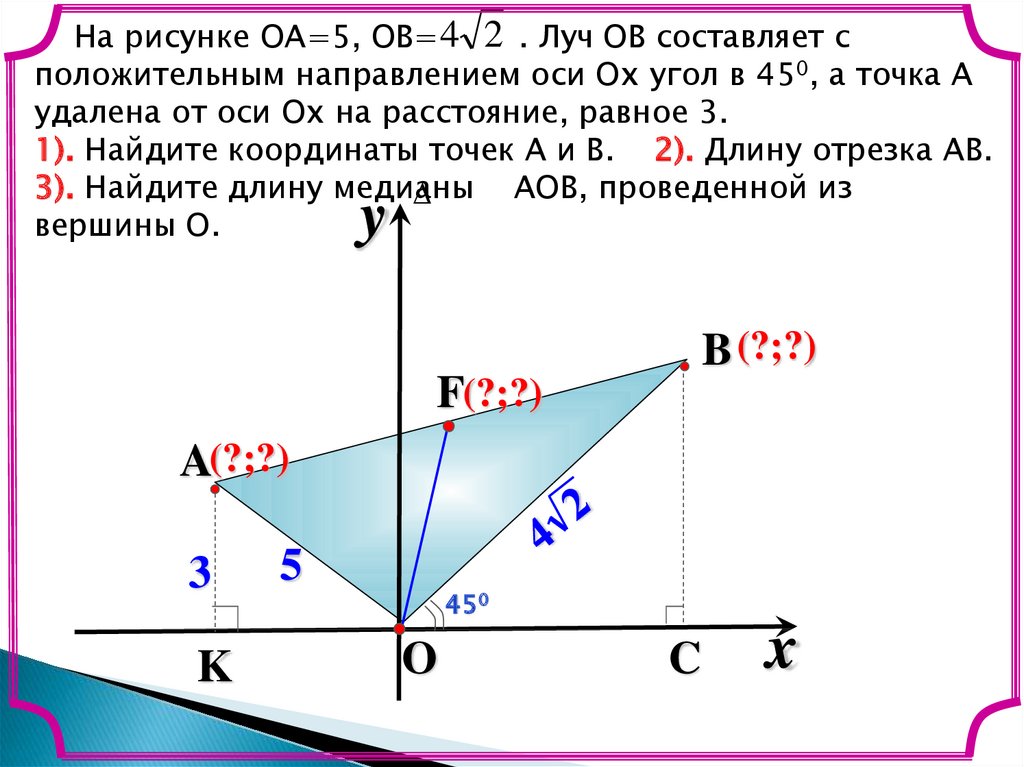
18.
На рисунке ОА=5, ОВ= 4 2 . Луч ОВ составляет сположительным направлением оси Ох угол в 450, а точка А
удалена от оси Ох на расстояние, равное 3.
1). Найдите координаты точек А и В. 2). Длину отрезка АВ.
3). Найдите длину медианы
АОВ, проведенной из
вершины О.
y
B (?;?)
F(?;?)
A(?;?)
3
K
5
450
O
C
x
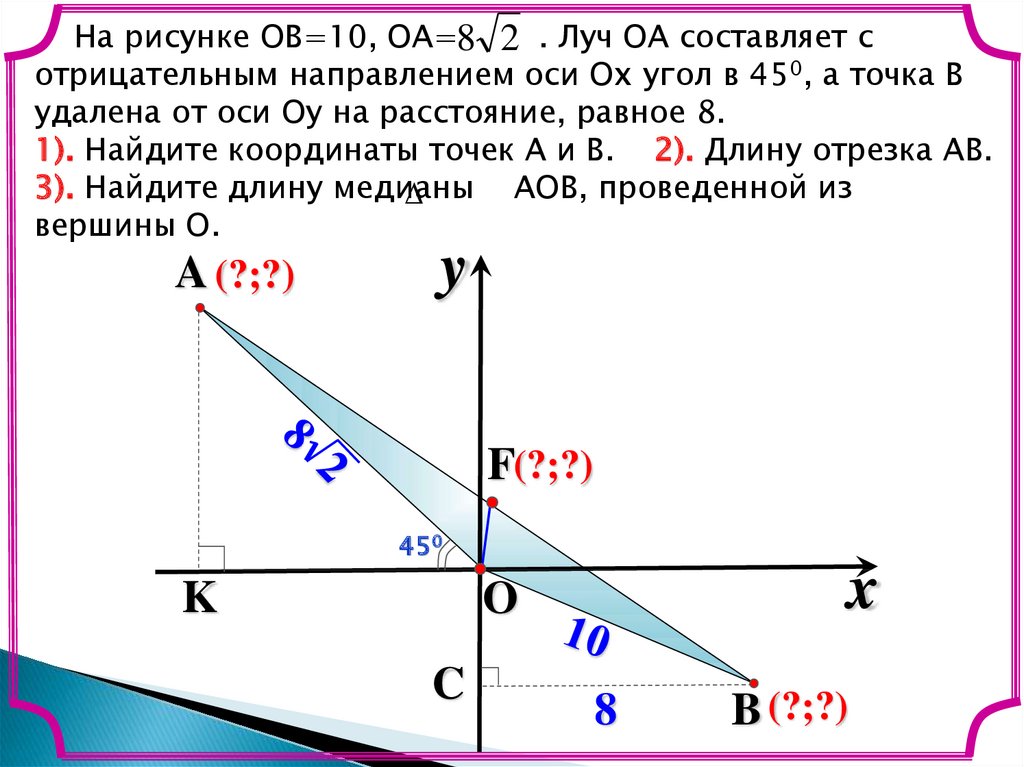
19.
На рисунке ОВ=10, ОА=8 2 . Луч ОА составляет сотрицательным направлением оси Ох угол в 450, а точка В
удалена от оси Оу на расстояние, равное 8.
1). Найдите координаты точек А и В. 2). Длину отрезка АВ.
3). Найдите длину медианы
АОВ, проведенной из
вершины О.
A (?;?)
y
F(?;?)
450
K
x
O
C
8
B (?;?)








 mathematics
mathematics








