Similar presentations:
Алгоритм Дейкстры
1. Алгоритм Дейкстры
©2014, Serge Kashkevich2.
Задан взвешенный граф с N вершинами иM рёбрами. Для каждого ребра задано
его расстояние – неотрицательная
величина. Требуется найти минимальное
расстояние от вершины 1 до всех
остальных вершин (вариант –
минимальное расстояние между заданной
парой вершин).
3. Типы пометок вершин
отсутствует – не найдено ни одногопути до этой вершины;
временная – путь найден, но он,
возможно, не минимален;
постоянная – найден минимальный путь
4.
23
2
4
5
9
4
5
25
1
2
6
7
3
21
11
24
7
3
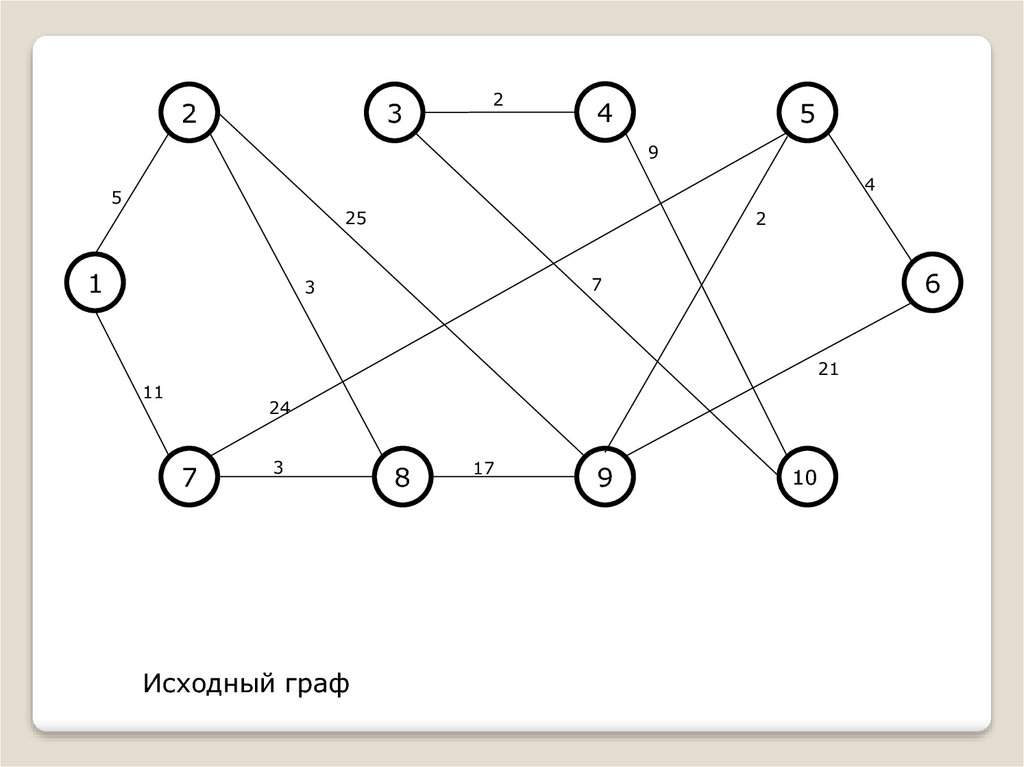
Исходный граф
8
17
9
10
5.
23
2
4
5
9
4
5
25
1
2
6
7
3
21
12
24
7
3
8
17
9
10
1
0
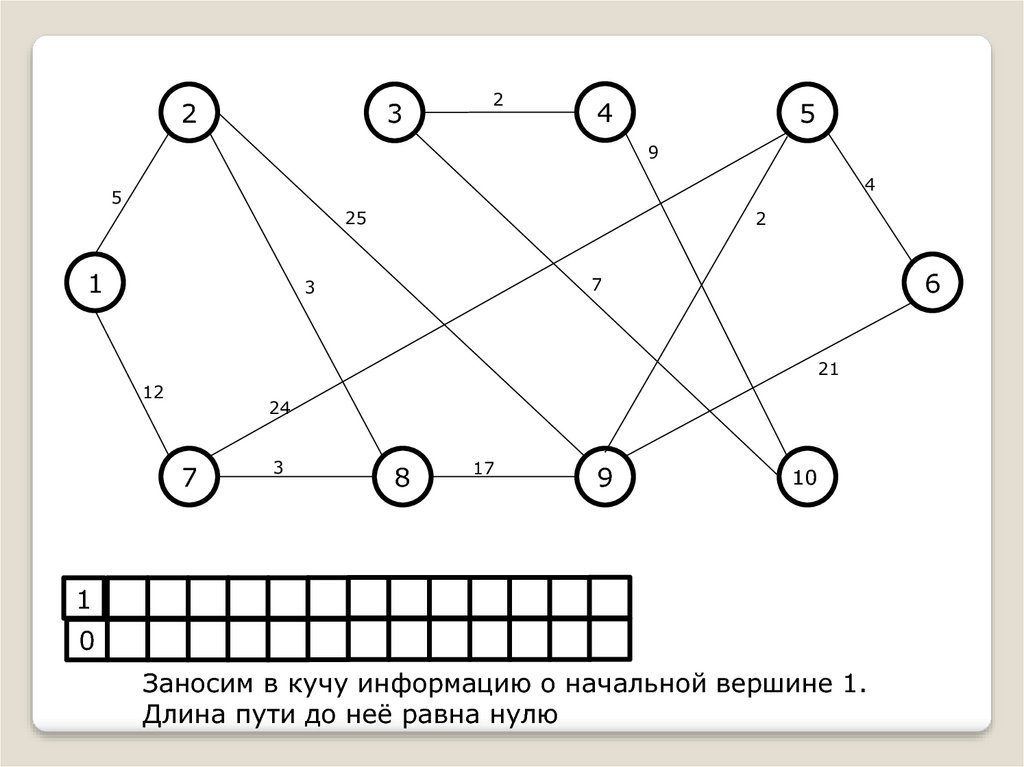
Заносим в кучу информацию о начальной вершине 1.
Длина пути до неё равна нулю
6.
5 23
2
4
5
9
4
5
25
2
0
1
6
7
3
21
12
12 7
1
2
7
0
5
12
24
3
8
17
9
10
Извлекаем вершину 1, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 2 и 7
7.
5 23
2
4
5
9
4
5
25
2
0
1
6
7
3
21
12
24
3
12 7
1
2
7
8
9
0
5
12
8
30
8
8
30
17
9
10
Извлекаем вершину 2, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 8 и 9
8.
5 23
2
4
5
9
4
5
25
2
0
1
6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
8
25
17
9
10
9
30 11 25
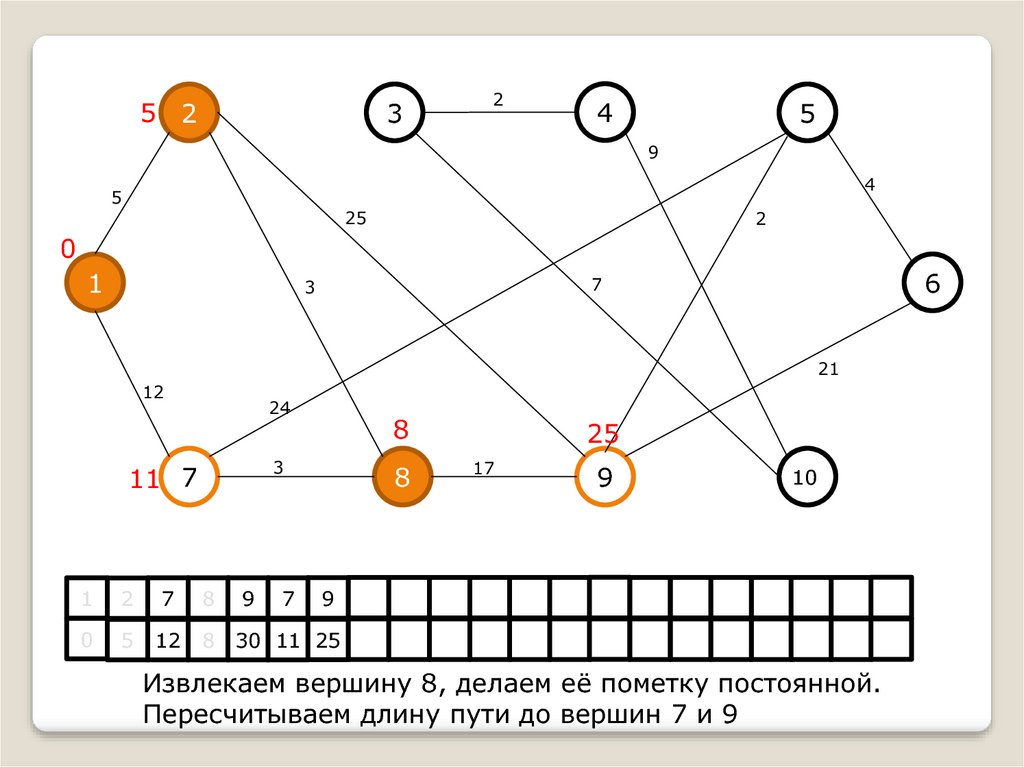
Извлекаем вершину 8, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 7 и 9
9.
5 23
2
35 5
4
9
4
5
25
2
0
1
6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
8
9
25
17
9
10
5
30 11 25 35
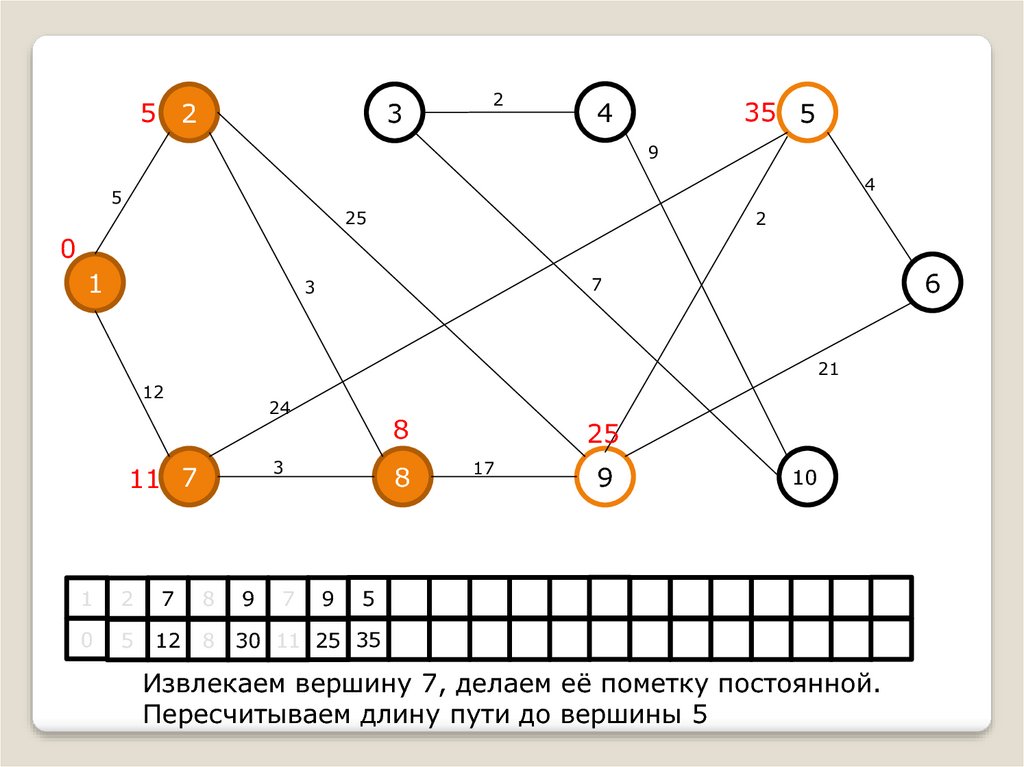
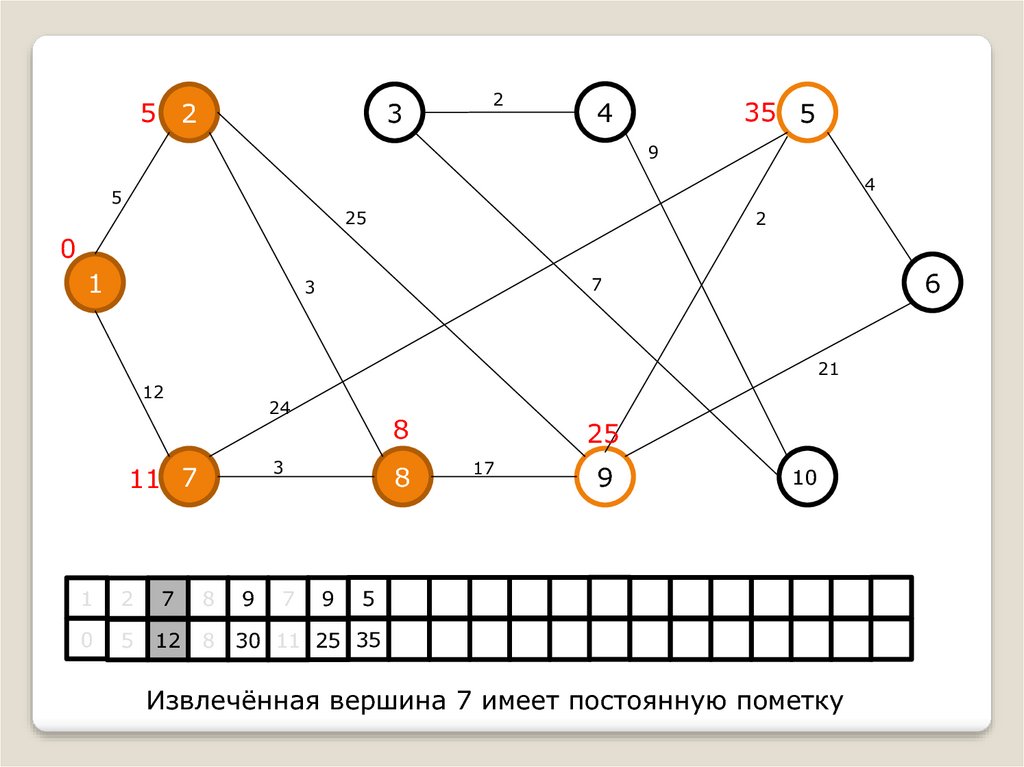
Извлекаем вершину 7, делаем её пометку постоянной.
Пересчитываем длину пути до вершины 5
10.
5 23
2
35 5
4
9
4
5
25
2
0
1
6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
8
9
25
17
9
10
5
30 11 25 35
Извлечённая вершина 7 имеет постоянную пометку
11.
5 22
3
27 5
4
9
4
5
25
2
0
1
46 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
9
10
6
30 11 25 35 27 46
Извлекаем вершину 9, делаем её пометку постоянной.
Пересчитываем длину пути до вершин 5 и 6
12.
5 22
3
27 5
4
9
4
5
25
2
0
1
31 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
6
9
10
6
30 11 25 35 27 46 31
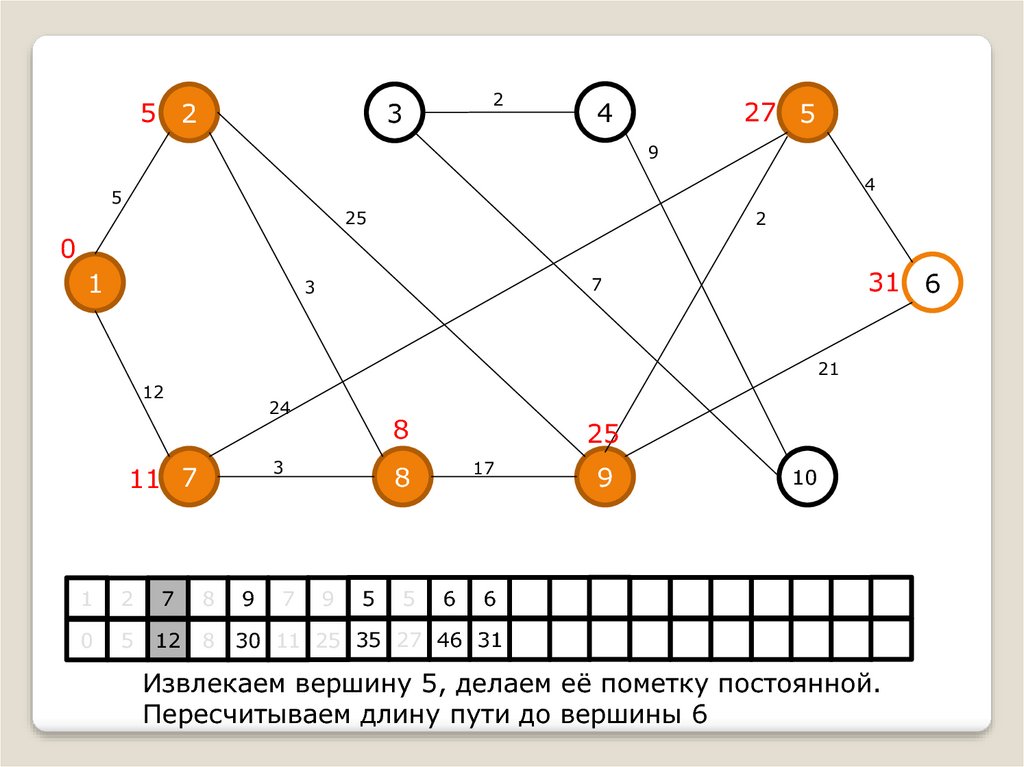
Извлекаем вершину 5, делаем её пометку постоянной.
Пересчитываем длину пути до вершины 6
13.
5 22
3
27 5
4
9
4
5
25
2
0
1
31 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
6
9
10
6
30 11 25 35 27 46 31
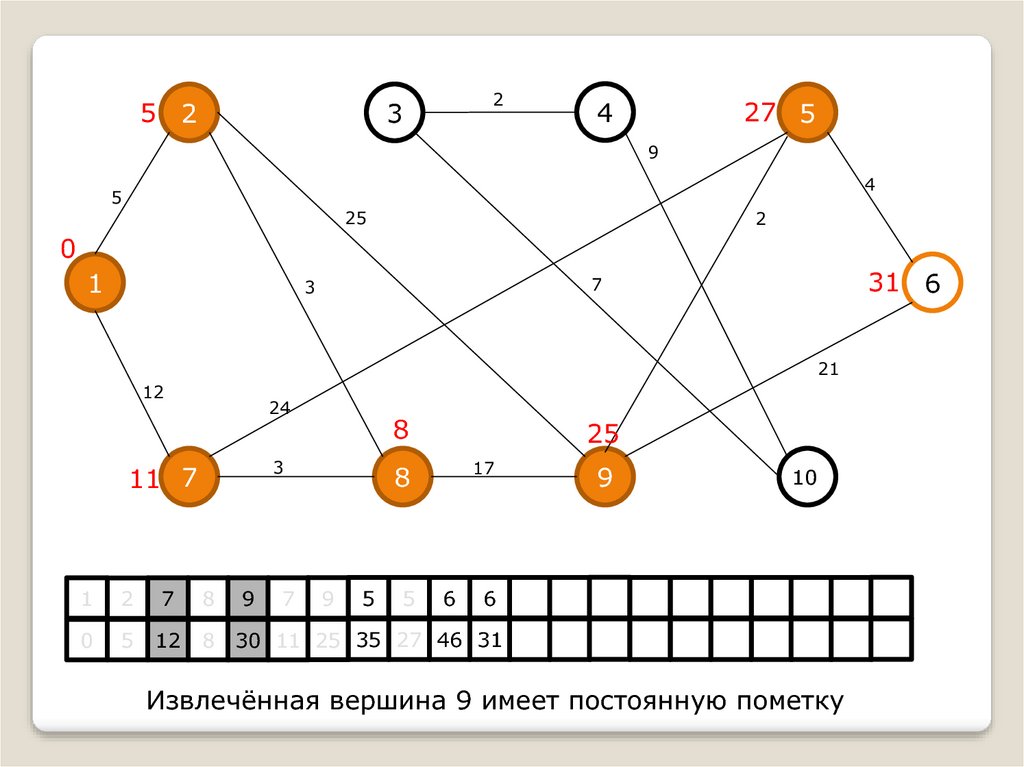
Извлечённая вершина 9 имеет постоянную пометку
14.
5 22
3
27 5
4
9
4
5
25
2
0
1
31 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
6
9
10
6
30 11 25 35 27 46 31
Извлекаем вершину 6, делаем её пометку постоянной
15.
5 22
3
27 5
4
9
4
5
25
2
0
1
31 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
6
9
10
6
30 11 25 35 27 46 31
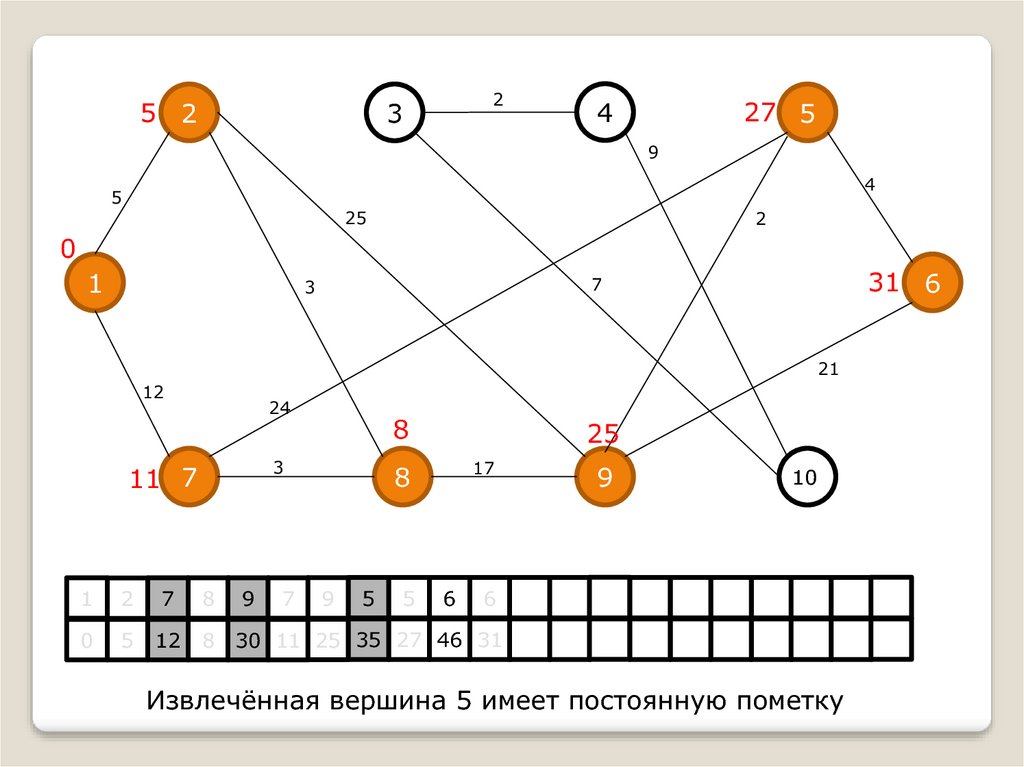
Извлечённая вершина 5 имеет постоянную пометку
16.
5 22
3
27 5
4
9
4
5
25
2
0
1
31 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
6
9
10
6
30 11 25 35 27 46 31
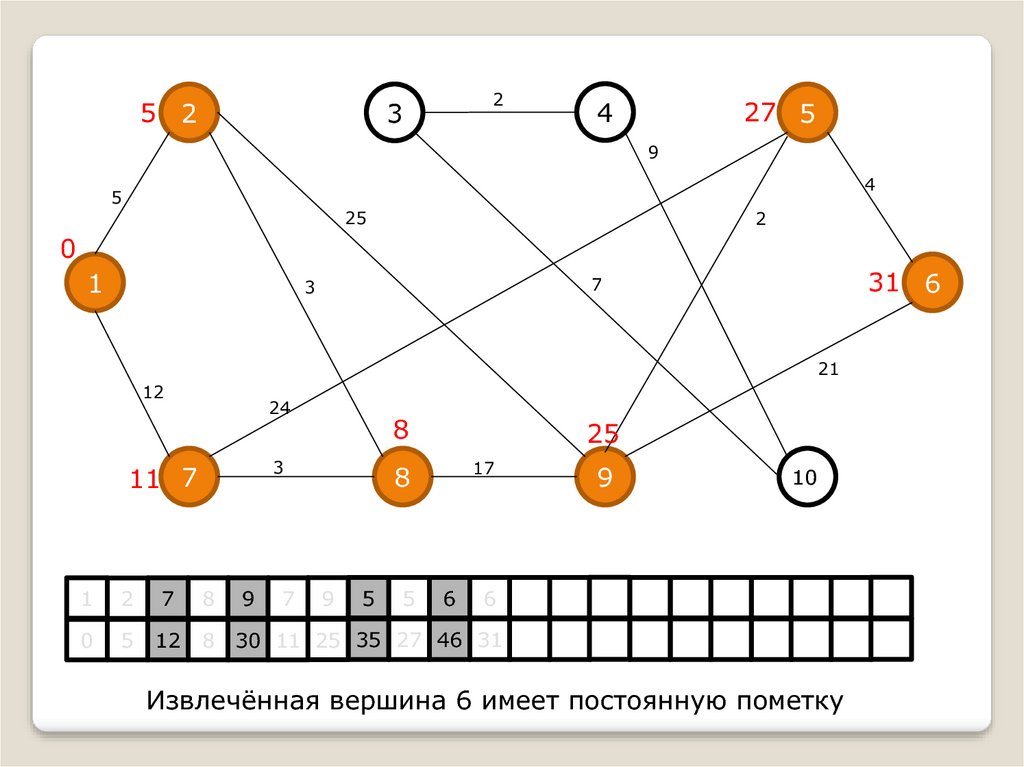
Извлечённая вершина 6 имеет постоянную пометку
17.
5 22
3
27 5
4
9
4
5
25
2
0
1
31 6
7
3
21
12
24
8
3
11 7
1
2
7
8
0
5
12
8
9
7
25
17
8
9
5
5
6
9
10
6
30 11 25 35 27 46 31
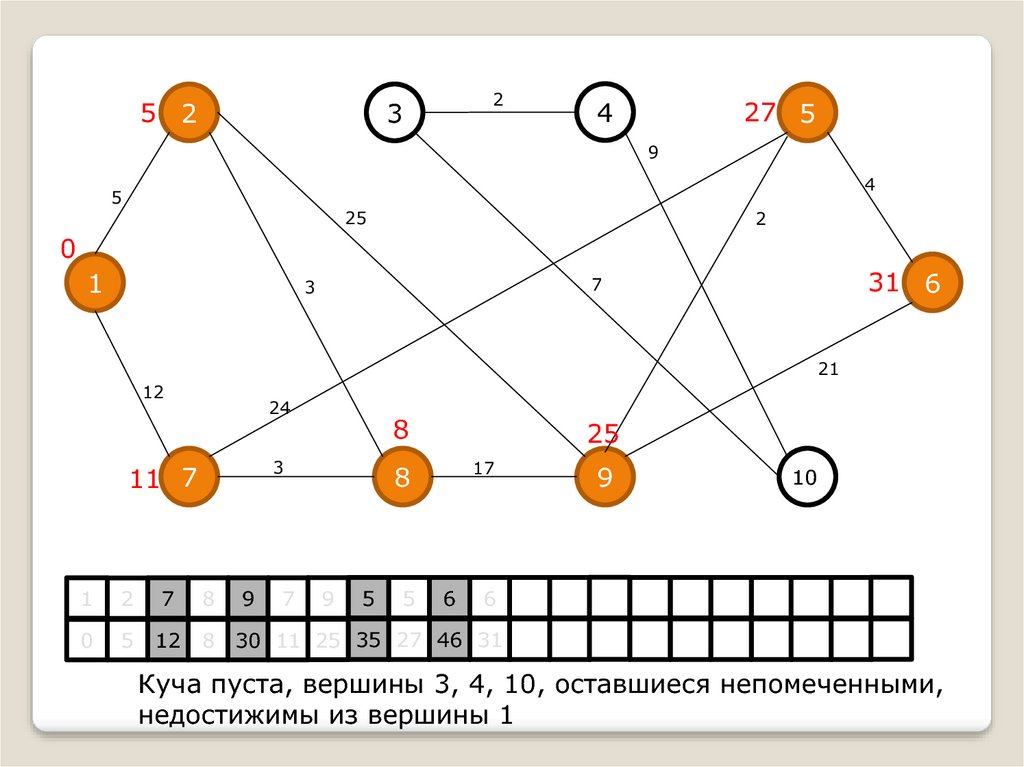
Куча пуста, вершины 3, 4, 10, оставшиеся непомеченными,
недостижимы из вершины 1







 programming
programming








