Теория алгоритмов. Алгоритмы сортировки массивов. (Лекция 2)

1. Теория алгоритмов

Лекция № 2
Алгоритмы сортировки массивов

2. Алгоритм сортировки

• Сортировка - это процесс упорядочения
некоторого множества элементов, на
котором определены отношения порядка
>, <, і , Ј .
• Задачей сортировки является
преобразование исходной последовательности
в последовательность, содержащую те же
элементы, но в порядке возрастания (или
убывания) значений.

3. Критерии оценки алгоримов

• Время — основной параметр, характеризующий
быстродействие алгоритма. Для типичного
алгоритма хорошее поведение — это O(n log n) и
плохое поведение — это O(n²). Идеальное
поведение для упорядочения — O(n). Алгоритмы
сортировки, использующие только абстрактную
операцию сравнения ключей всегда нуждаются
по меньшей мере в O(n log n) сравнениях в
среднем;
• Память — ряд алгоритмов требует выделения
дополнительной памяти под временное хранение
данных. При оценке используемой памяти не
будет учитываться место, которое занимает
исходный массив и независящие от входной
последовательности затраты, например, на
хранение кода программы.

4. Классификация алгоритмов сортировки

• Устойчивость (stability) — устойчивая сортировка не
меняет взаимного расположения равных элементов.
• Естественность поведения — эффективность
метода при обработке уже упорядоченных, или
частично упорядоченных данных. Алгоритм ведёт
себя естественно, если учитывает эту характеристику
входной последовательности и работает лучше.
• Использование операции сравнения. Алгоритмы,
использующие для сортировки сравнение элементов
между собой, называются основанными на
сравнениях. Минимальная трудоемкость худшего
случая для этих алгоритмов составляет O(n log n) ,
но они отличаются гибкостью применения. Для
специальных случаев (типов данных) существуют
более эффективные алгоритмы.

5. Классификация по области применения

• Внутренняя сортировка оперирует с массивами,
целиком помещающимися в оперативной памяти с
произвольным доступом к любой ячейке. Данные
обычно упорядочиваются на том же месте, без
дополнительных затрат.
• Внешняя сортировка оперирует с запоминающими
устройствами большого объёма, но с доступом не
произвольным, а последовательным (упорядочение
файлов). Это накладывает некоторые
дополнительные ограничения на алгоритм и
приводит к специальным методам упорядочения,
обычно использующим дополнительное дисковое
пространство. Кроме того, доступ к данным на
носителе производится намного медленнее, чем
операции с оперативной памятью.

6. Также алгоритмы классифицируются по:

• потребности в дополнительной памяти
или её отсутствии;
• потребности в знаниях о структуре
данных, выходящих за рамки операции
сравнения, или отсутствии таковой .

7. Алгоритмы устойчивой сортировки

Сортировка обменная (пузырьком) (англ. Bubble sort ) — сложность
алгоритма: O(n2); для каждой пары индексов производится обмен, если
элементы расположены не по порядку.
Сортировка перемешиванием (Шейкерная, Cocktail sort, bidirectional bubble
sort) — Сложность алгоритма: O(n2)
Гномья сортировка — имеет общее с сортировкой пузырьком и
сортировкой вставками. Сложность алгоритма — O(n2).
Сортировка вставками (Insertion sort) — Сложность алгоритма: O(n2);
определяем где текущий элемент должен находиться в упорядоченном
списке и вставляем его туда
Блочная сортировка (Корзинная сортировка, Bucket sort) — Сложность
алгоритма: O(n); требуется O(k) дополнительной памяти и знание о природе
сортируемых данных, выходящее за рамки функций "переставить" и
"сравнить".
Сортировка подсчётом (Counting sort) — Сложность алгоритма: O(n+k);
требуется O(n+k) дополнительной памяти (рассмотрено 3 варианта)
Сортировка слиянием (Merge sort) — Сложность алгоритма: O(n log n);
требуется O(n) дополнительной памяти; выстраиваем первую и вторую
половину списка отдельно, а затем — сливаем упорядоченные списки
Сортировка с помощью двоичного дерева (англ. Tree sort) — Сложность
алгоритма: O(n log n); требуется O(n) дополнительной памяти

8. Алгоритмы неустойчивой сортировки

Сортировка выбором (Selection sort) — Сложность алгоритма:
O(n2); поиск наименьшего или наибольшего элемента и помещения
его в начало или конец упорядоченного списка
Сортировка Шелла (Shell sort) — Сложность алгоритма: O(n log2 n);
попытка улучшить сортировку вставками
Сортировка расчёской (Comb sort) — Сложность алгоритма: O(n
log n)
Пирамидальная сортировка (Сортировка кучи, Heapsort) —
Сложность алгоритма: O(n log n); превращаем список в кучу, берём
наибольший элемент и добавляем его в конец списка
Плавная сортировка (Smoothsort) — Сложность алгоритма: O(n log
n)
Быстрая сортировка (Quicksort) — Сложность алгоритма: O(n log
n) — среднее время, O(n2) — худший случай;
Поразрядная сортировка (Цифровая сортировка) — Сложность
алгоритма: O(n·k); требуется O(k) дополнительной памяти.

9. Прочие алгоритмы сортировки

Сортировка перестановкой — O(n·n!) — худшее время. Для
каждой пары осуществляется проверка верного порядка и
генерируются всевозможные перестановки исходного массива.
Глупая сортировка (Stupid sort) — O(n3); рекурсивная версия
требует дополнительно O(n2) памяти
Блинная сортировка (Pancake sorting) — O(n), требуется
специализированное аппаратное обеспечение
Лексикографическая или поразрядная сортировка (Radix
sort)
Сортировка подсчётом (Counting sort)
Топологическая сортировка
Внешняя сортировка

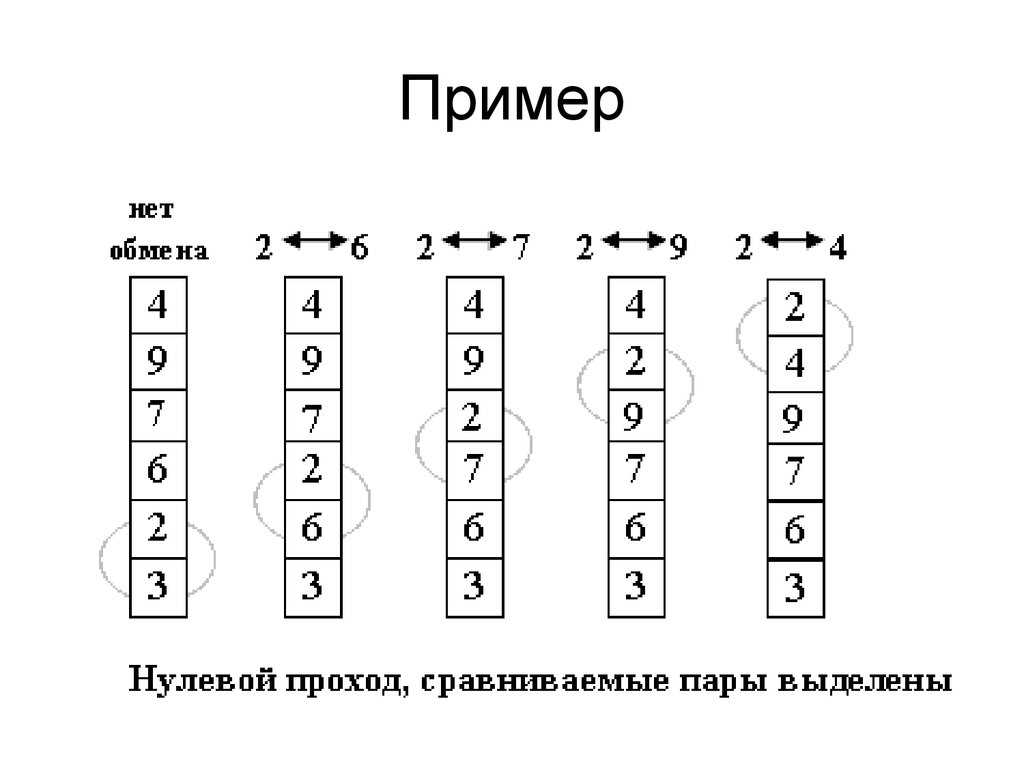
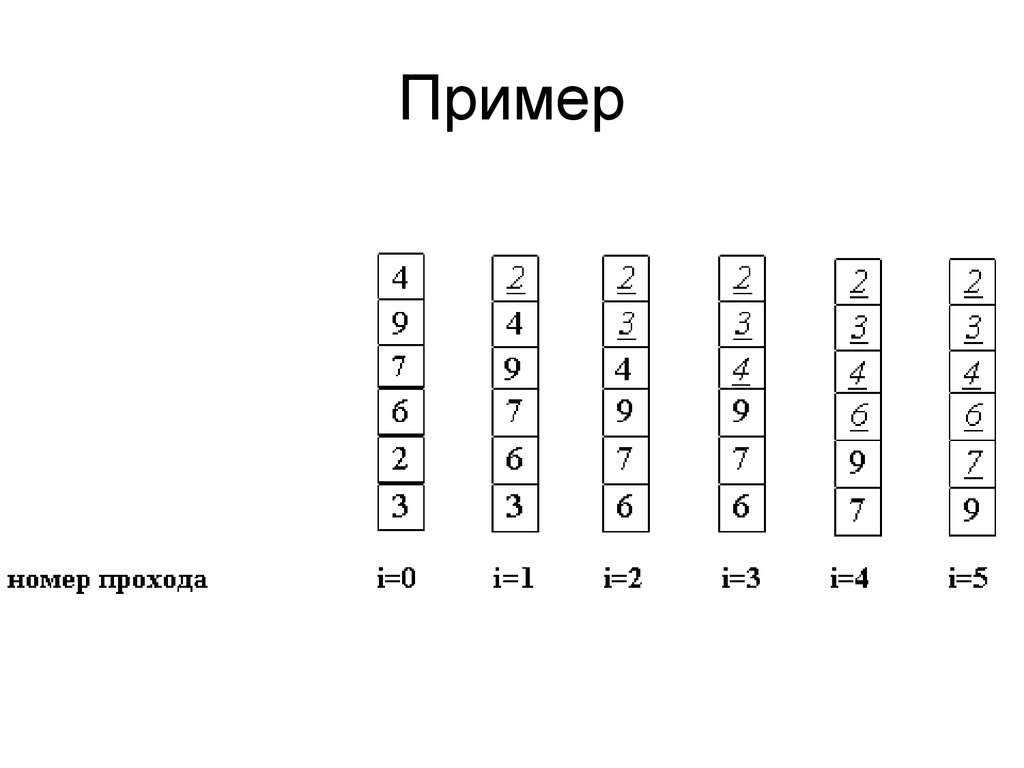
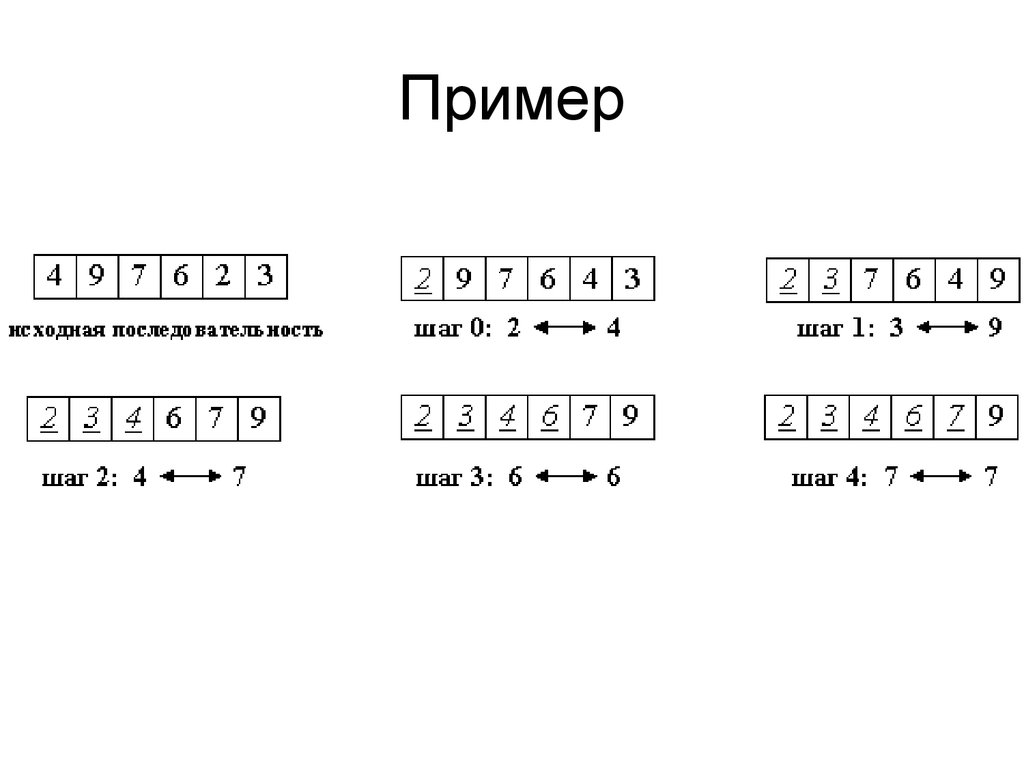
10. Сортировка обменом (пузырьковая сортировка)

Идея метода: шаг сортировки состоит в
проходе снизу вверх по массиву. По
пути просматриваются пары соседних
элементов. Если элементы некоторой
пары находятся в неправильном
порядке, то меняем их местами.

11. Пример

12. Пример

13.

Сортировка «пузырьком»
for (int i = 1; i < n; i++) {
for (int j = 0; j < n-i; j++) {
if (data[j] > data [j+1]) {
int tmp = data[j];
data[j] = data[j+1];
data[j+1] = tmp;
}
}
}
4 27 51 14 31 42 1
4 27 14 31 42 1
4 14 27 31 1
4 14 27 1
4 14 1
4
1
8 24 3 59 33 44 53 16 10 38 50 21 36
8 24 3 51 33 44 53 16 10 38 50 21 36 59
8 24 3 42 33 44 51 16 10 38 50 21 36 53 59
8 24 3 31 33 42 44 16 10 38 50 21 36 51 53 59
8 24 3 27 31 33 42 16 10 38 44 21 36 50 51 53 59
8 14 3 24 27 31 33 16 10 38 42 21 36 44 50 51 53 59

14. Оптимизация алгоритма

• Запоминаем, производился ли на данном проходе
какой-либо обмен. Если нет - алгоритм заканчивает
работу.
• Запоминаем индекс последнего обмена k.
Действительно: все пары соседих элементов с
индексами, меньшими k, уже расположены в нужном
порядке. Дальнейшие проходы можно заканчивать на
индексе k, вместо того чтобы двигаться до
установленной заранее верхней границы i.
• Меняем направление следующих один за другим
проходов. Получившийся алгоритм иногда называют
"шейкер-сортировкой".

15. Сортировка выбором

Идея метода состоит в том, чтобы создавать
отсортированную последовательность путем
присоединения к ней одного элемента за
другим в правильном порядке.
Суть алгоритма: Построить готовую
упорядоченную последовательность, начиная
с левого конца массива.
Алгоритм состоит из n последовательных шагов,
начиная от нулевого и заканчивая (n-1)-м.
На i-м шаге выбираем наименьший из элементов
a[i] ... a[n] и меняем его местами с a[i].

16. Пример

17. Сортировка вставками

Идея алгоритма: Предположим последовательность
a[0]...a[i] упорядочена. При этом по ходу алгоритма в
нее будут вставляться все новые элементы.
Суть алгоритма: На i-м шаге последовательность
разделена на две части: готовую a[0]...a[i] и
неупорядоченную a[i+1]...a[n].
На следующем, (i+1)-м каждом шаге алгоритма берем
a[i+1] и вставляем на нужное место в готовую часть
массива.
Поиск подходящего места для очередного элемента
входной последовательности осуществляется путем
последовательных сравнений с элементом, стоящим
перед ним.
В зависимости от результата сравнения элемент либо
остается на текущем месте(вставка завершена), либо
они меняются местами и процесс повторяется.

18. Пример

19.

Сортировка простыми вставками
4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 14 27 51 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 14 27 31 51 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 14 27 31 42 51 1
8 24 3 59 33 44 53 16 10 38 50 21 36
int i, j;
for (i = 1; i < n; i++) {
int c = data[i];
for (j = i-1; j >= 0 && data[j] > c; j--) {
data[j+1] = data[j];
}
data[j+1] = c;
}

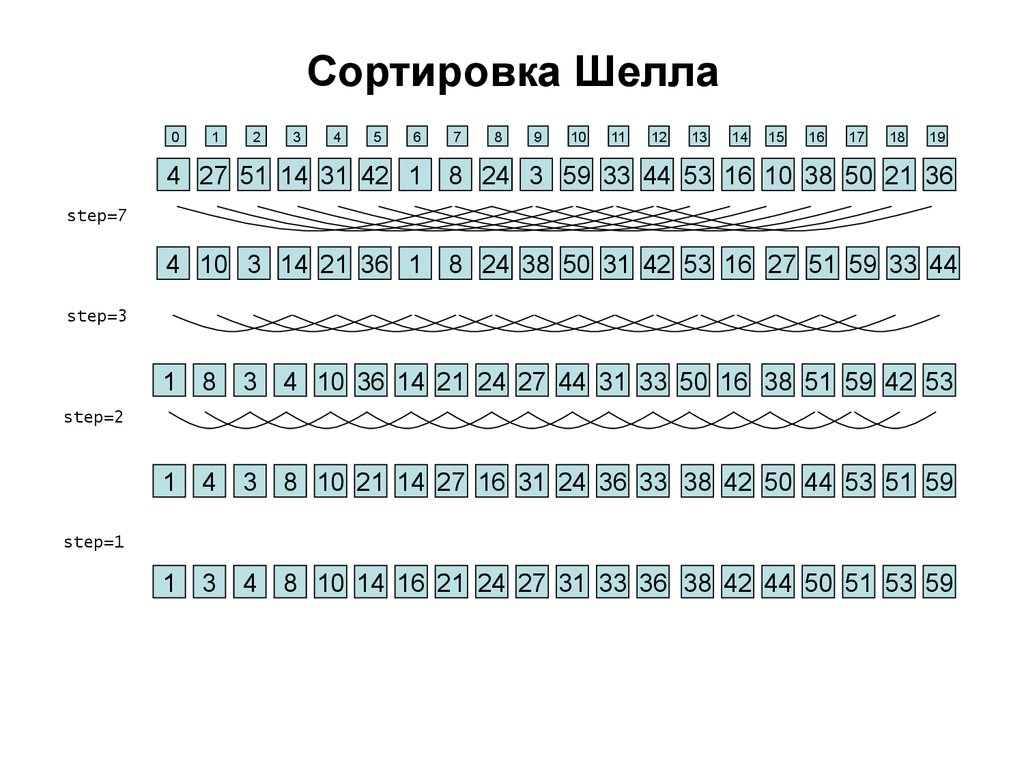
20. Сортировка Шелла

Сортировка Шелла (англ. Shell sort) — алгоритм
сортировки, идея которого состоит в сравнении
элементов, стоящих не только рядом, но и на
расстоянии друг от друга. Иными словами —
сортировка вставками с предварительными
«грубыми» проходами.
При сортировке Шелла сначала сравниваются и
сортируются между собой ключи, отстоящие один от
другого на некотором расстоянии d. После этого
процедура повторяется для некоторых меньших
значений d, а завершается сортировка Шелла
упорядочиванием элементов при d = 1 (то есть,
обычной сортировкой вставками).

21.

Сортировка Шелла
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 38 50 21 36
4 10 3 14 21 36 1
8 24 38 50 31 42 53 16 27 51 59 33 44
step=7
step=3
1
8
3
4 10 36 14 21 24 27 44 31 33 50 16 38 51 59 42 53
1
4
3
8 10 21 14 27 16 31 24 36 33 38 42 50 44 53 51 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59
step=2
step=1

22.

Сортировка Шелла
int n ;
// Длина массива
int step = n;
// Шаг поисков и вставки
int i, j;
do {
// Вычисляем новый шаг
step = step / 3 + 1;
// Производим сортировку простыми вставками с заданным шагом
for (i = step; i < n; i++) {
int c = data[i];
for (j = i-step; j >= 0 && data[j] > c; j -= step) {
data[j+step] = data[j];
}
data[j+step] = c;
}
} while (step != 1);
Количество перестановок элементов
(по результатам экспериментов со случайным массивом)
n = 25
n = 1000
n = 100000
Сортировка Шелла
50
7700
2 100 000
Сортировка простыми вставками
150
240 000
2.5 млрд.

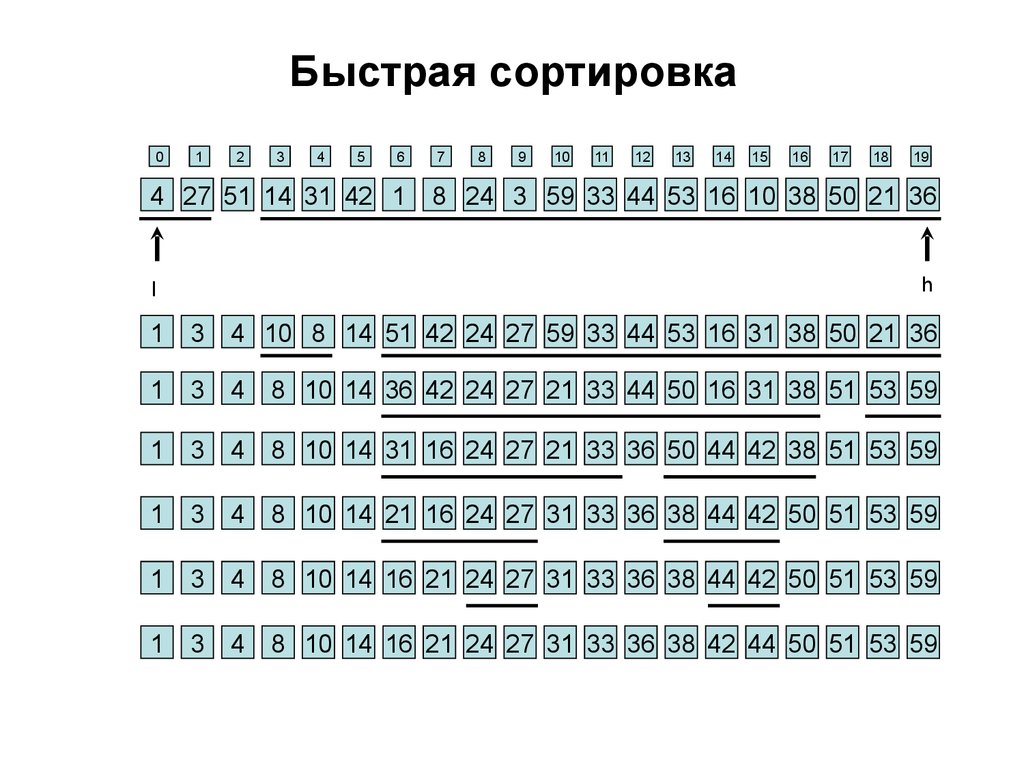
23. Быстрая сортировка

Быстрая сортировка (англ. quicksort) — широко
известный алгоритм сортировки, разработанный
английским информатиком Чарльзом Хоаром. Один
из быстрых известных универсальных алгоритмов
сортировки массивов (в среднем O(n log n) обменов
при упорядочении n элементов), хотя и имеющий ряд
недостатков.
Краткое описание алгоритма
• выбрать элемент, называемый опорным.
• сравнить все остальные элементы с опорным, на
основании сравнения разбить множество на три —
«меньшие опорного», «равные» и «большие»,
расположить их в порядке меньшие-равные-большие.
• повторить рекурсивно для «меньших» и «больших».

24.

Быстрая сортировка
0
1
2
3
4
5
6
4 27 51 14 31 42 1
7
8
9
10
11
12
13
14
15
16
17
18
19
8 24 3 59 33 44 53 16 10 38 50 21 36
h
l
1
3
4 10 8 14 51 42 24 27 59 33 44 53 16 31 38 50 21 36
1
3
4
8 10 14 36 42 24 27 21 33 44 50 16 31 38 51 53 59
1
3
4
8 10 14 31 16 24 27 21 33 36 50 44 42 38 51 53 59
1
3
4
8 10 14 21 16 24 27 31 33 36 38 44 42 50 51 53 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 44 42 50 51 53 59
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59

25. Быстрая сортировка

26.

Дополнения и улучшения алгоритма
Первый элемент в сортируемом куске выбирается случайно и запоминается;
Участки, меньшие определенного размера, сортируются простыми способами;
Иногда исключение рекурсивных вызовов приводит к повышению эффективности.

27.

Алгоритм слияния упорядоченных массивов
4
14
27
51
1
3
8
24
31
42
59
int na, // длина массива a[]
nb, // длина массива b[]
nc;
int[] c = new int[nc = na + nb];
int ia = 0,
ib = 0,
ic = 0;
while (ia < na && ib < nb) {
if (a[ia] < b[ib])
c[ic++] = a[ia++];
else
c[ic++] = b[ib++];
}
while (ia < na) c[ic++] = a[ia++];
while (ib < nb) c[ic++] = b[ib++];

28.

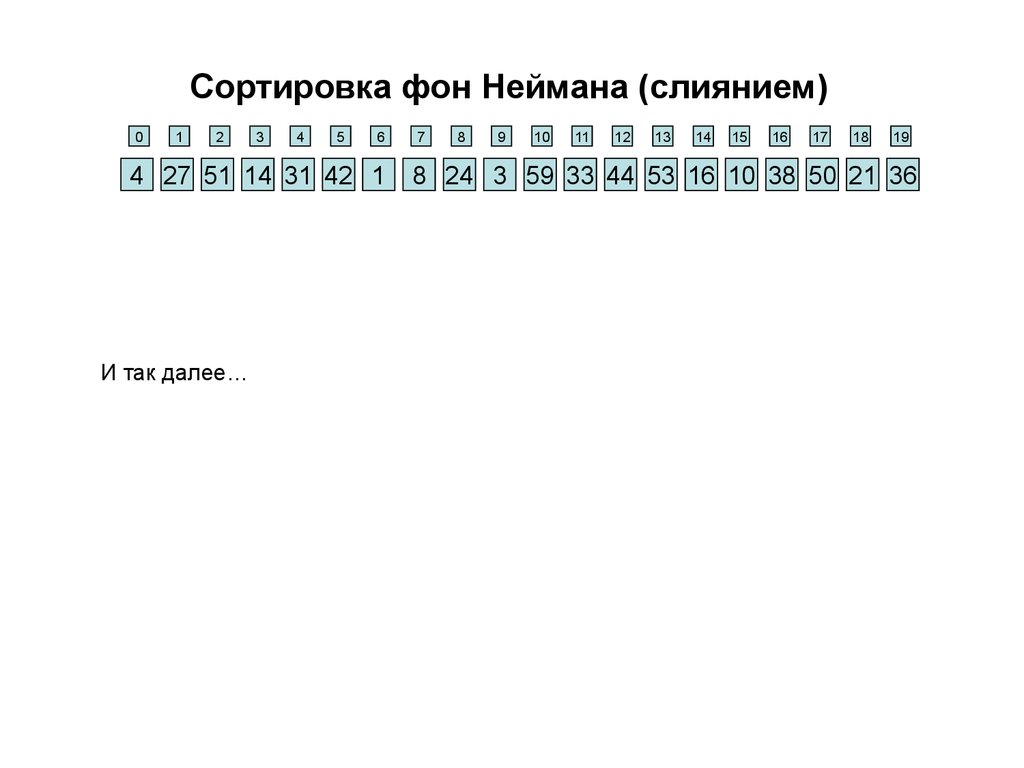
Сортировка фон Неймана (слиянием)
0
1
2
3
4
5
6
4 27 51 14 31 42 1
И так далее…
7
8
9
10
11
12
13
14
15
16
17
18
19
8 24 3 59 33 44 53 16 10 38 50 21 36

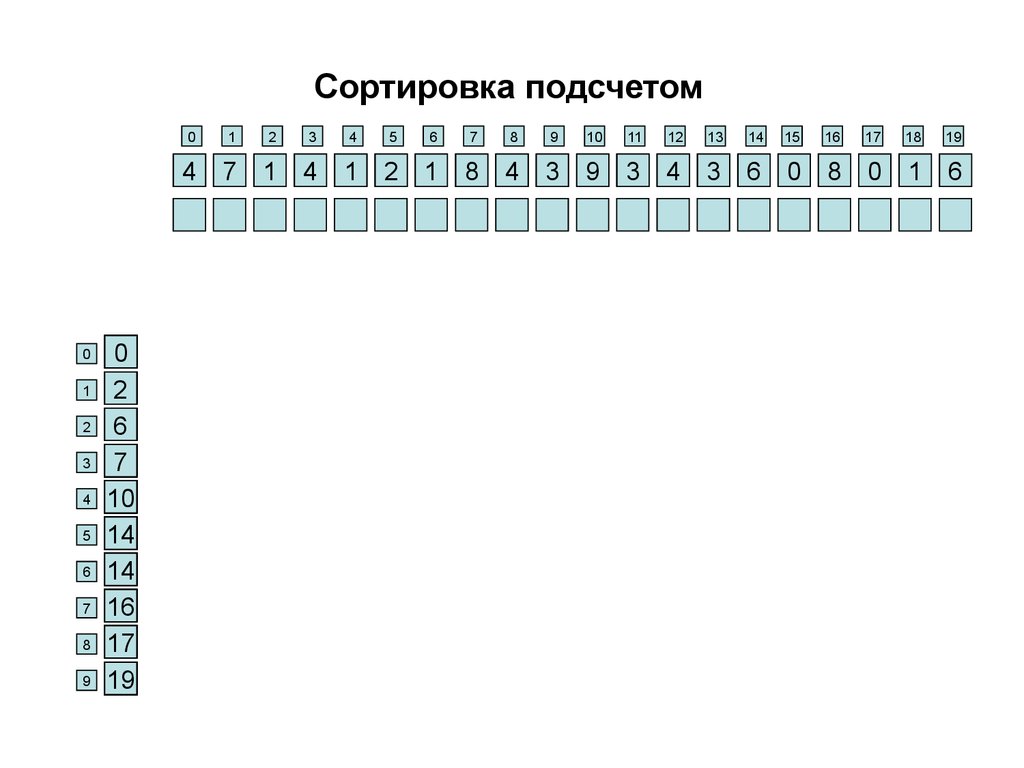
29. Сортировка подсчетом

Этот алгоритм подходит для сортировки целых чисел из
не очень большого диапазона (сравнимого с размером
массива).
Идея алгоритма: для каждого элемента найти, сколько
элементов, меньших определенного числа, и поместить
это число на соответствующие место. За линейный
проход по массиву для каждого из возможных значений
подсчитываем, сколько элементов имеют такое
значение. Потом добавляем к каждому из найденных
чисел суму всех предыдущих. Получая, таким образом,
сколько есть элементов, значения которых не больше
данного значения. Далее, опять-таки за линейный
проход, формируем из исходного массива новый
отсортированный.

30.

Сортировка подсчетом
0
1
2
3
4
5
6
7
8
9
2
1
0
6
5
4
3
2
1
7
6
10
3
9
8
7
14
13
12
10
11
4
14
0
16
15
14
2
17
16
1
19
18
17
2
20
19
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
4
7
1
4
1
2
1
8
4
3
9
3
4
3
6
0
8
0
1
6

31. Цифровая сортировка

Цифровая сортировка — один из
алгоритмов сортировки, использующих
внутреннюю структуру сортируемых
объектов. Алгоритм состоит в
последовательной сортировке объектов
какой-либо устойчивой сортировкой по
каждому разряду, в порядке от младшего
разряда к старшему, после чего
последовательности будут расположены в
требуемом порядке.

32.

Цифровая сортировка
4 27 51 14 31 42 1
8 24 3 59 33 44 53 16 10 39 50 21 36
После сортировки по последней цифре:
10 50 51 31 1 21 42 3 33 53 4 14 24 44 16 36 27 8 59 39
После устойчивой сортировки по первой цифре:
1
3
4
8 10 14 16 21 24 27 31 33 36 39 42 44 50 51 53 59

33. Алгоритмы поиска

• Одно из наиболее часто встречающихся
в программировании действий этопоиск. Существует несколько основных
вариантов поиска, и для них создано
много различных алгоритмов.

34. Линейный поиск

• Данный алгоритм является простейшим
алгоритмом поиска и в отличие, например, от
двоичного поиска, не накладывает никаких
ограничений на функцию и имеет
простейшую реализацию. Поиск значения
функции осуществляется простым
сравнением очередного рассматриваемого
значения (как правило поиск происходит
слева направо, т.е. от меньших значений
аргумента к большим) и, если значения
совпадают (с той или иной точностью), то
поиск считается завершённым.

35. Двоичный поиск

• Двоичный поиск (также известен, как метод
деления пополам и метод половинного
деления) — алгоритм нахождения заданного
значения монотонной (невозрастающей или
неубывающей) функции. Поиск основывается
на теореме о промежуточных значениях.
Используется в информатике,
вычислительной математике и
математическом программировании.

36. Двоичный поиск в упорядоченном массиве

33
0
1
2
3
1
3
4
8 10 14 16 21 24 27 31 33 36 38 42 44 50 51 53 59
l
4
5
6
7
8
9
m
10
11
12
13
14
15
16
17
18
19
h

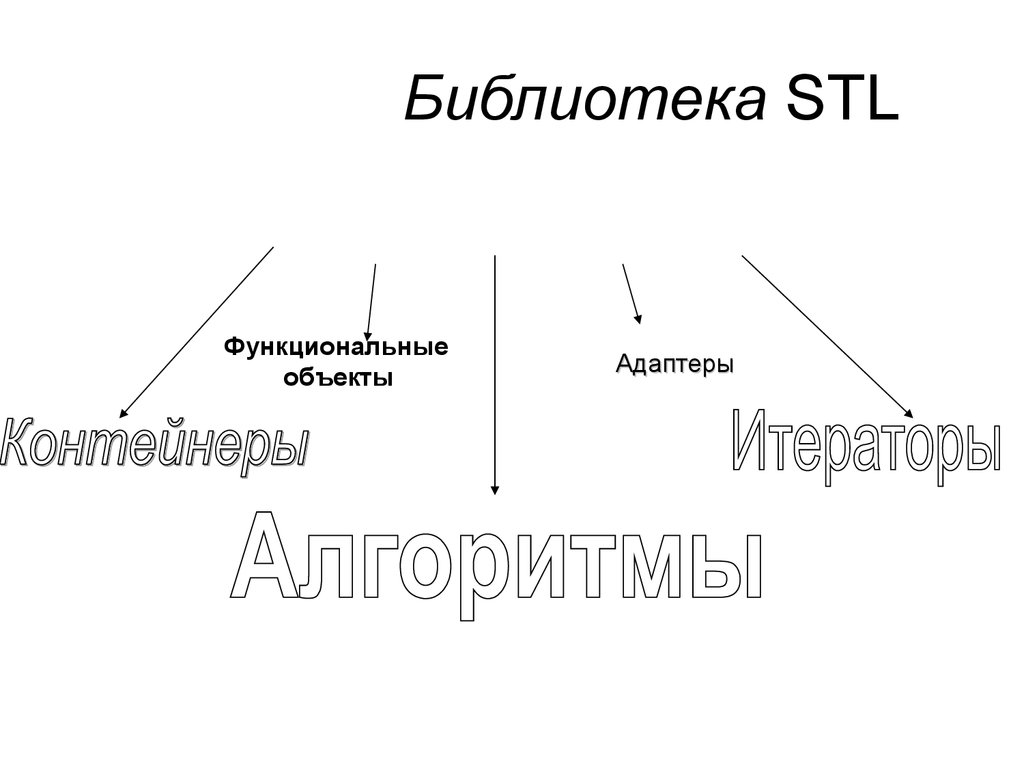
37. Библиотека STL

Функциональные
объекты
Адаптеры

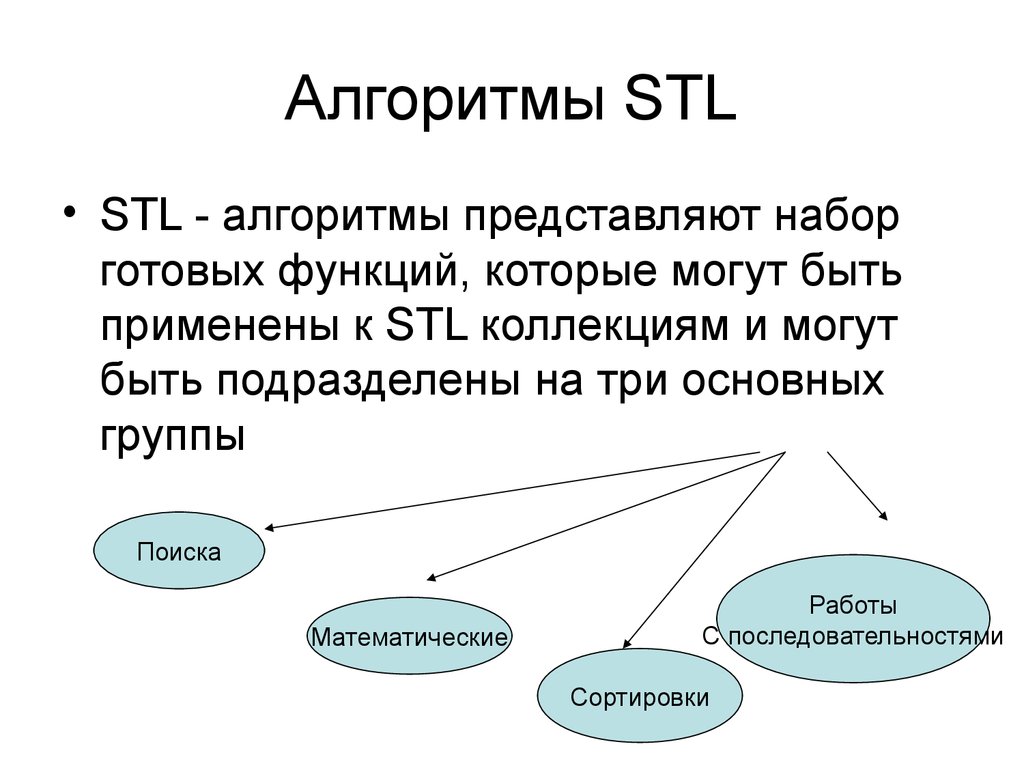
38. Алгоритмы STL

• STL - алгоритмы представляют набор
готовых функций, которые могут быть
применены к STL коллекциям и могут
быть подразделены на три основных
группы
Поиска
Математические
Работы
С последовательностями
Сортировки

39. Функции для сортировки членов коллекции

• sort, stable_sort, partial_sort,
partial_sort_copy, nth_element,
binary_search, lower_bound, upper_bound,
equal_range, merge, inplace_merge,
includes, set_union, set_intersection,
set_difference, set_symmetric_difference,
make_heap, push_heap, pop_heap,
sort_heap, min, max, min_element,
max_element, lexographical_compare,
next_permutation, prev_permutation