Similar presentations:
Биологические потенциалы
1.
Раздел: Биофизика мембранных процессовТема: Биологические потенциалы
2.
ПОТЕНЦИАЛ ПОКОЯ3. Биологические потенциалы
• Основная функция БМ-генерация ипередача биопотенциалов
Основа возбудимости клеток
Регуляция внутриклеточных процессов
Регуляция работы нервной системы
Регуляция мышечного сокращения
Регуляция рецепции
4. ЭП позволяют
• Электрокардиография (активность сердца)• Электроэнцефалография (активность
головного мозга)
• Электромиография (мышечная активность)
5. Электрические потенциалы
• Окислительно-восстановительные –вследствие переноса электронов от одних
молекул к другим
• Мембранные – возникают вследствие
градиента концентрации ионов по разные
стороны мембраны
Мембранные потенциалы – биопотенциалы,
которые в основном регистрируются в
организме
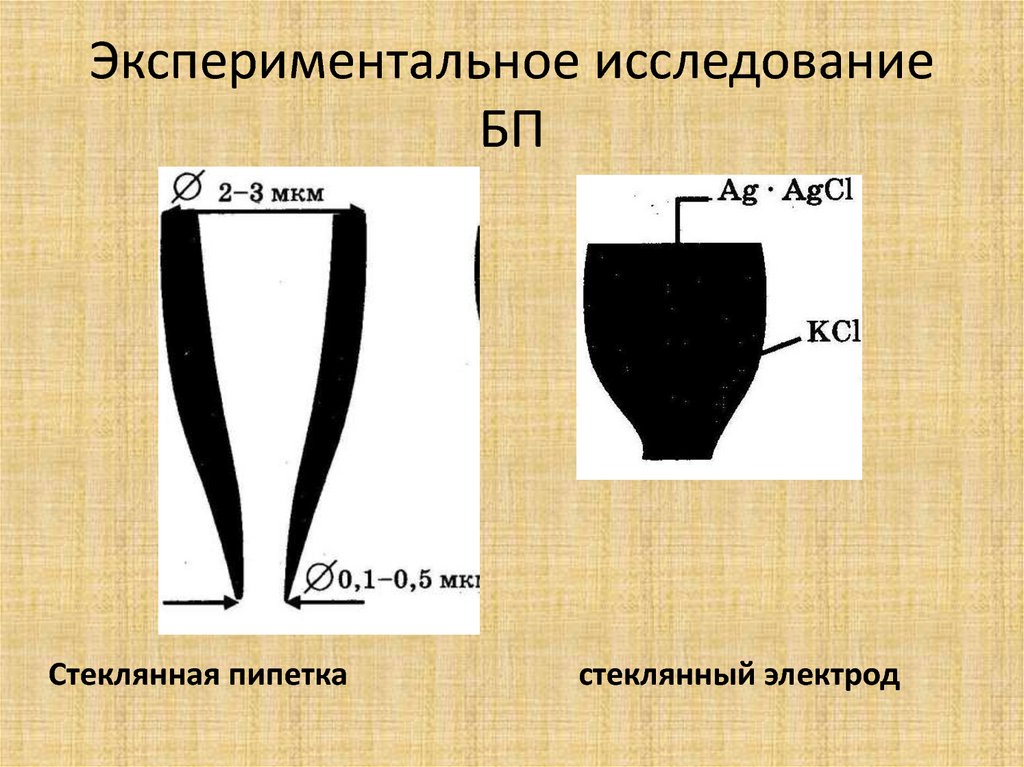
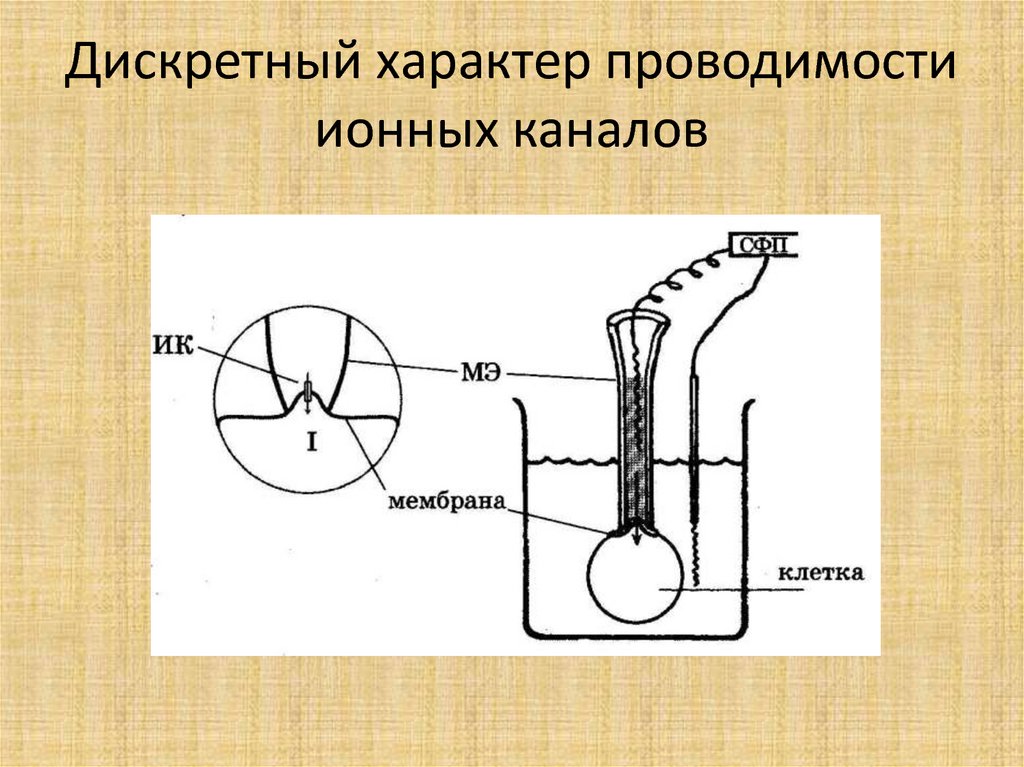
6. Экспериментальное исследование БП
• Разработка микроэлектродного методавнутриклеточного измерения БП
• Создание специальных усилителей БП
• Выбор объекта исследования – крупные
клетки – АКСОН КАЛЬМАРА
( 0,5мм > позвоночных)
7. Экспериментальное исследование БП
Стеклянная пипеткастеклянный электрод
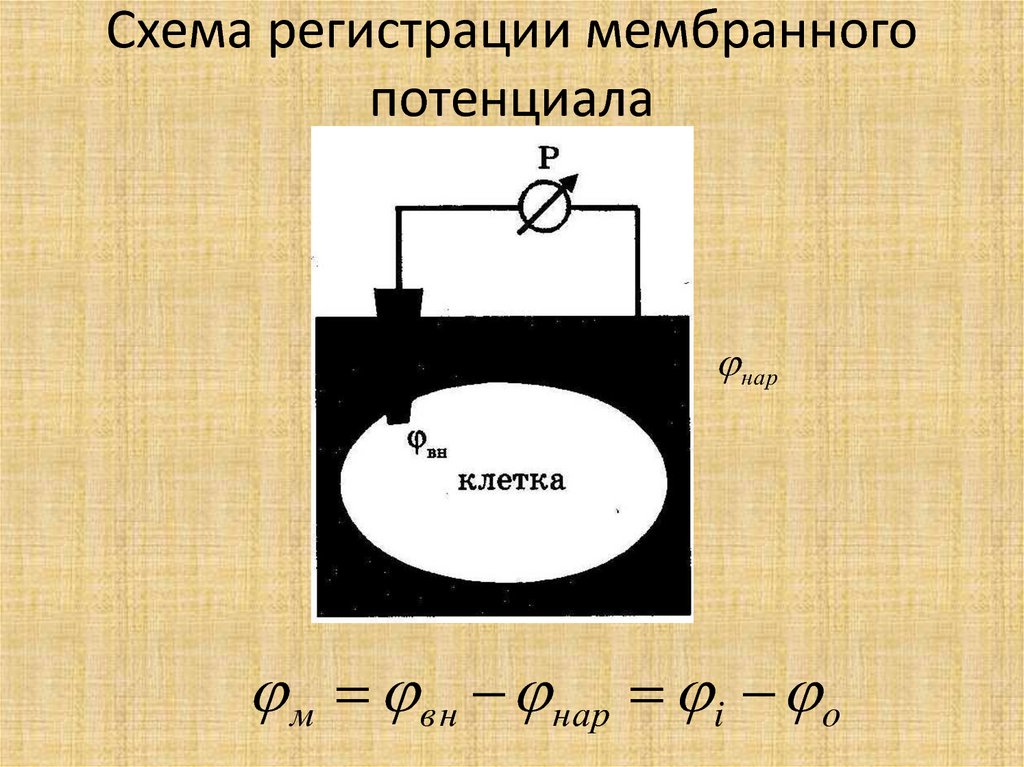
8. Схема регистрации мембранного потенциала
нарм в н нар i o
9. Виды потенциалов
Потенциал покояПотенциал действия
- разная концентрация ионов
- диффузия ионов через БМ
м в н нар i o
10. Потенциал покоя
м в н нар i o• Стационарная разность потенциалов в
клетке, регистрируемая между наружной и
внутренней поверхностью мембраны,
находящейся в невозбужденном состоянии
• Обусловлен различными концентрациями
ионов во внутриклеточном и наружном
растворах
11.
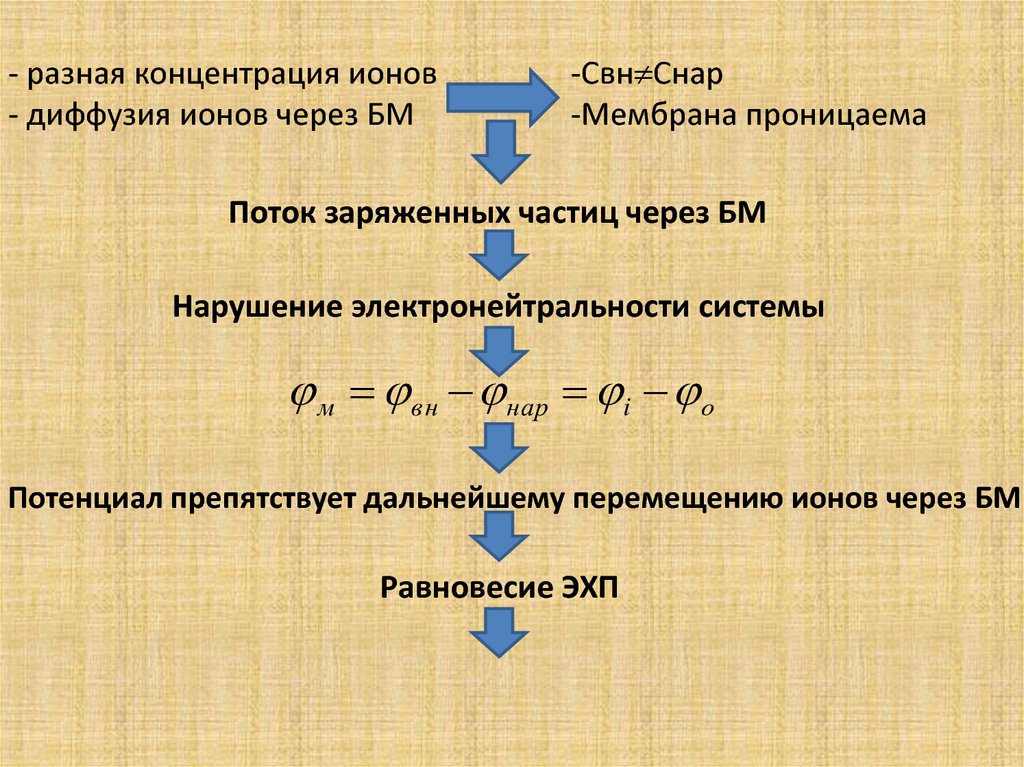
- разная концентрация ионов- диффузия ионов через БМ
-Свн Снар
-Мембрана проницаема
Поток заряженных частиц через БМ
Нарушение электронейтральности системы
м в н нар i o
Потенциал препятствует дальнейшему перемещению ионов через БМ
Равновесие ЭХП
12.
Равновесие ЭХПвн нар
0 RT ln C ZF
RT ln Cвн ZF вн RT ln Cнар ZF нар
формула Нернста-Планка
для равновесного мембранного потенциала
вн нар
р
м
Cвн
RT Cнар
RT
ln
ln
ZF Cвн
ZF Cнар
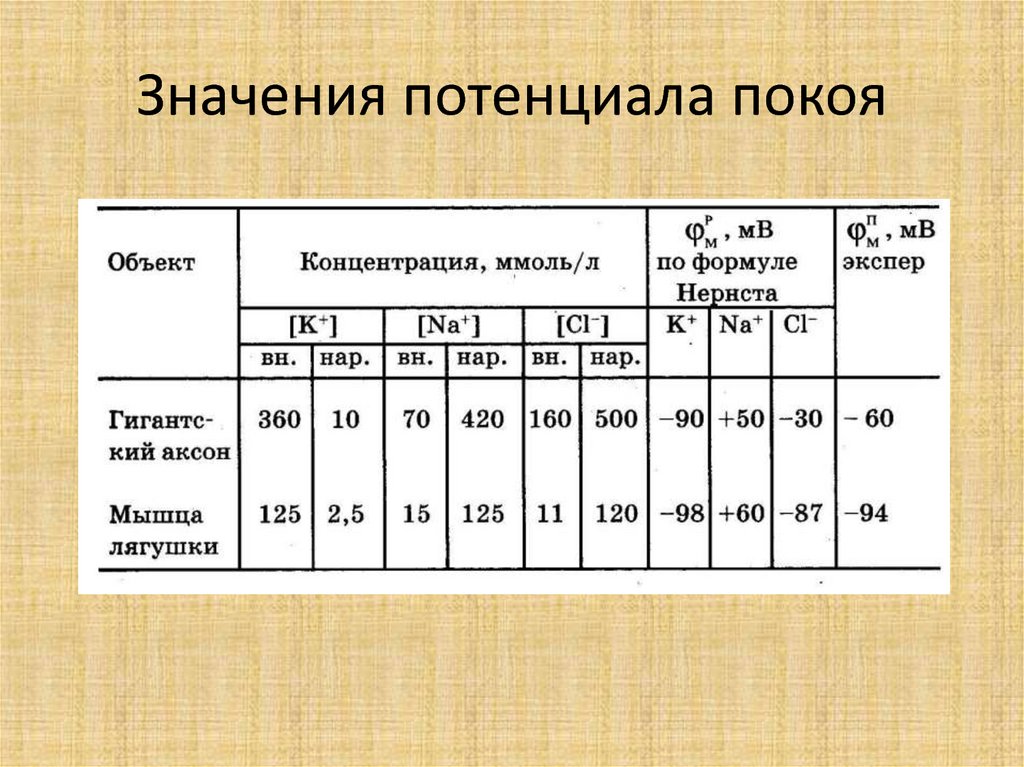
13. Значения потенциала покоя
14. Формула Нернста-Планка для равновесного мембранного потенциала
CвнRT
ln
ZF Cнар
р
м
Z
1
RT
K
вн
мр, K
ln
0
ZF
K нар
K в н K нар
Z
1
RT
Na
вн
мр, Na
ln
0
ZF
Na нар
Na в н Na нар
Z
1
RT
Cl
вн
мр,Cl
ln
0
ZF
Cl нар
Cl в н Cl нар
15. Электродиффузионный транспорт через БМ
Элетродиффузия – пассивный транспорт ионов через БМвн нар
1. Отсутствуют суммарные ионные токи:
Потенциал Нернста определяется концентрацией ионов в
растворе
Cвн
RT
ln
ZF Cнар
р
м
2. Ионные токи не равны 0: вн нар
Пассивное движение ионов по градиенту ЭХП
возникает диффузионная разность потенциалов, которая
зависит от:
- Ионных концентраций
- Подвижности ионов
16. Способы описания процесса перехода ионов через БМ
• Дискретный• Непрерывный
Ионы преодолевают БМ с
помощью нескольких
дискретных перескоков
через активационные
барьеры
Ионы движутся через БМ
независимо и не
взаимодействуя друг с
другом. БМ является
гомогенной фазой
Описание транспорта ионов
через селективные
каналы клеточной
мембраны
Описание транспорта
ионов через
искусственные БЛМ
17. Непрерывное описание диффузии
• Уравнение Нернста-Планка:0 RT ln C ZF
d
dC
d
URT
J CU
UZFC
dx
dx
1. ЭХ равновесие dx
2. Отсутствие ЭХ равновесия
3. Приближение постоянного поля
18. ЭХ равновесие
1 2 J 01 dC
ZF d
C dx
RT dx
RT Co
0
2 1 м
ln
м
ZF Ci
Потенциал Нернста – определение равновесной разности
потенциалов на БМ – мембранный потенциал
19. Потенциал Нернста для одновалентных ионов
Дж8,3
* 300 К
Co
Co
0
Кмоль
м
2,3 * ln
0,06 ln
Кл
C
C
i
i
1* 96500
моль
экспер
0
К : м
м
• 1902г Берштейн – причина возникновения
мембранного потенциала – диффузия
ионов К+ из клетки во внеклеточную среду
20. Отсутствие ЭХ равновесия
• Подход Гендерсона-Планка:- Концентрация катионов и анионов в любой
плоскости, перпендикулярной
направлению переноса – одинаковая:
С+=С-=С
- В стационарном состоянии электрический
ток через БМ отсутствует
- Для бинарного электролита: Z+=-Z-=1
21. Отсутствие ЭХ равновесия
dCd
J URT
UZFC
dx
dx
J
J
dC
d
dC
d
U RT
U FC
U RT
U FC
dx
dx
dx
dx
d U U RT 1 dC
dx U U F C dx
U U RT Ci
2 1 м
ln
U U F
Co
22. Уравнение Гендерсона
U U RT C2м
ln
U U F
C1
U+ U—- подвижность катиона и аниона в БМ
расчет диффузионного потенциала, возникающего
между двумя электролитами
Уравнение Гендерсона применимо:
-Для мембран макроскопической толщины 1 мкм
-Не применимо для липидных и клеточных мембран, где
не выполняется условие локальной
электронейтральности по всей толщине мембраны
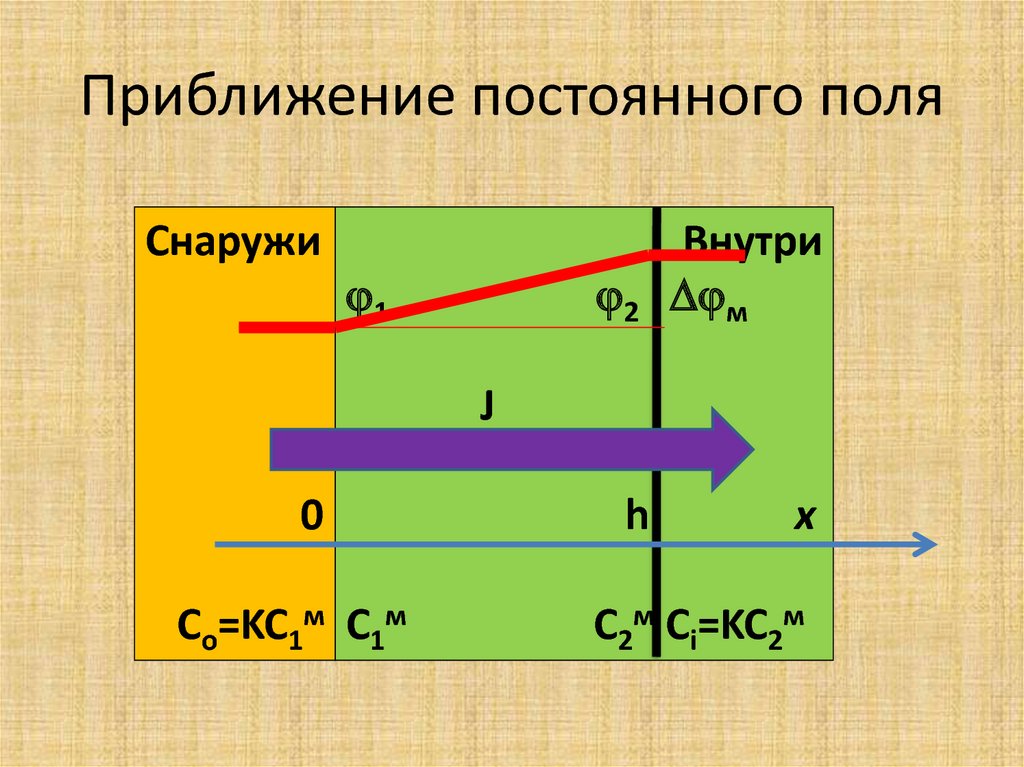
23. Приближение постоянного поля
• Предположение о линейности измененияпотенциала ЭП по всей толщине БМ
d
dx
E const
• Для тонких БМ, в которых концентрация
носителей мала, а толщина двойного слоя –
велика
24. Приближение постоянного поля
Снаружи1
2
Внутри
м
h
x
J
0
Co=KC1м C1м
C2м Ci=KC2м
25. Профиль поля - линеен
d мconst
dx
h
h
dC
d
J URT
UZFC
dx
dx
dC ZFC d
J
dx
RT dx
URT
dC
AC B
dx
C 2м
h
dC
м AC B 0 dx
C
1
26.
C 2мh
dC
м AC B 0 dx
C
1
м Ah
1
B C C e
Ah
A
e 1
м
2
ZF
C C exp
м
UFZ
RT
J
м
h
ZF
exp
м 1
RT
м
2
м
1
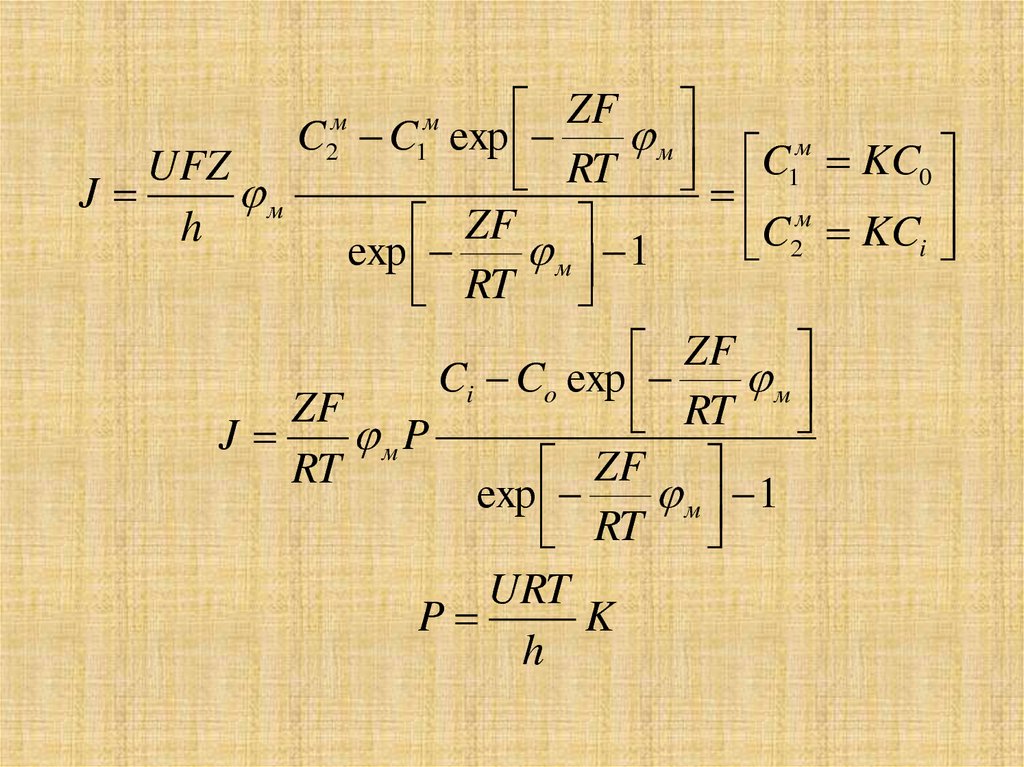
27.
ZFC C exp
м
м
C
UFZ
RT
1 KC0
J
м
м
h
ZF
C2 KCi
exp
м 1
RT
ZF
Ci Co exp
м
ZF
RT
J
мP
RT
ZF
exp
м 1
RT
URT
P
K
h
м
2
м
1
28.
URTP
K
h
• Р – коэффициент проницаемости БМ
• К – коэффициент растворения, который
зависит от липофильности иона
1943 Гольдман + 1949 Ходжкин и Катц
29. Разность потенциалов, создаваемая в БМ в результате совместной диффузии ионов
• В равновесииI K I Na I Cl 0
F м
PK K i PK K o exp
RT
F м
PNa Na i PK Na o exp
RT
F м
PCl Cl o PK Cl i exp
0
RT
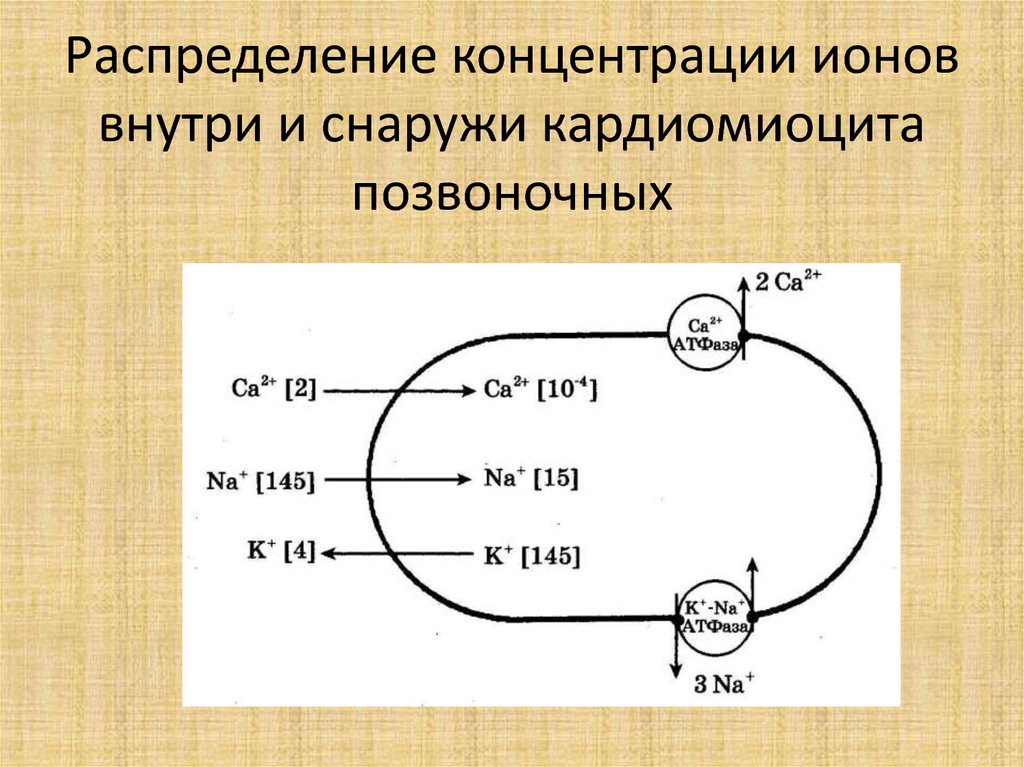
30.
RT PK K i PNa Na i PCl Cl oм
ln
F
PK K o PNa Na o PCl Cl i
• Потенциал на БМ определяется:
- Различием в стационарных концентрациях
ионов по обе стороны БМ
- Разными коэффициентами проницаемости
БМ для различных ионов
31. Соотношение Уссинга-Теорелла
J Ji JoZFP
J Ji
м
RT
Co
ZF
1 exp
м
RT
ZF
Ci exp
м
ZFP
RT
J Jo
м
RT
ZF
1 exp
м
RT
Ji
Co
Jo
ZF
Ci exp
м
RT
32. Критерии пассивного транспорта
• Поток ионов через БМ обусловлен:- Только градиентом концентрации ионнов кго типа
- Действием ЭП
- Нарушение соотношения Уссинга-Теорелла
– существование АКТИВНОГО ТРАНСПОРТА
33.
ПОТЕНЦИАЛ ДЕЙСТВИЯ34. Потенциал действия
• Открыт в 18 в. Луиджи Гальвани:• 1. мышечные сокращения
препарированной лягушки могут вызваться
электрическим импульсом
• 2. сама живая система является источником
электрического импульса
35. Потенциал действия
• 19в. Гельмгольц: показано, что скоростьраспространения нервного импульса (1-100
м/с) значительно меньше скорости
распространения электрического импульса
по проводам (3*108 м/с)
36. Потенциал действия
• 20 в. А.Ходжкин: нервный импульс-импульсэлектрического тока
• 1963 г. Ходжкин, Хаксли и Иклс –
Нобелевская премия по медицине «за
оперирование нервных клеток»
37. Потенциал действия
• Электрический импульс, обусловленныйизменением ионной проницаемости
мембраны и связанный с
распространением по нервам и мышцам
волны возбуждения
Методы:
1. Микроэлектродов с использованием
высокоомных измерителей напряжения
2. Меченных атомов
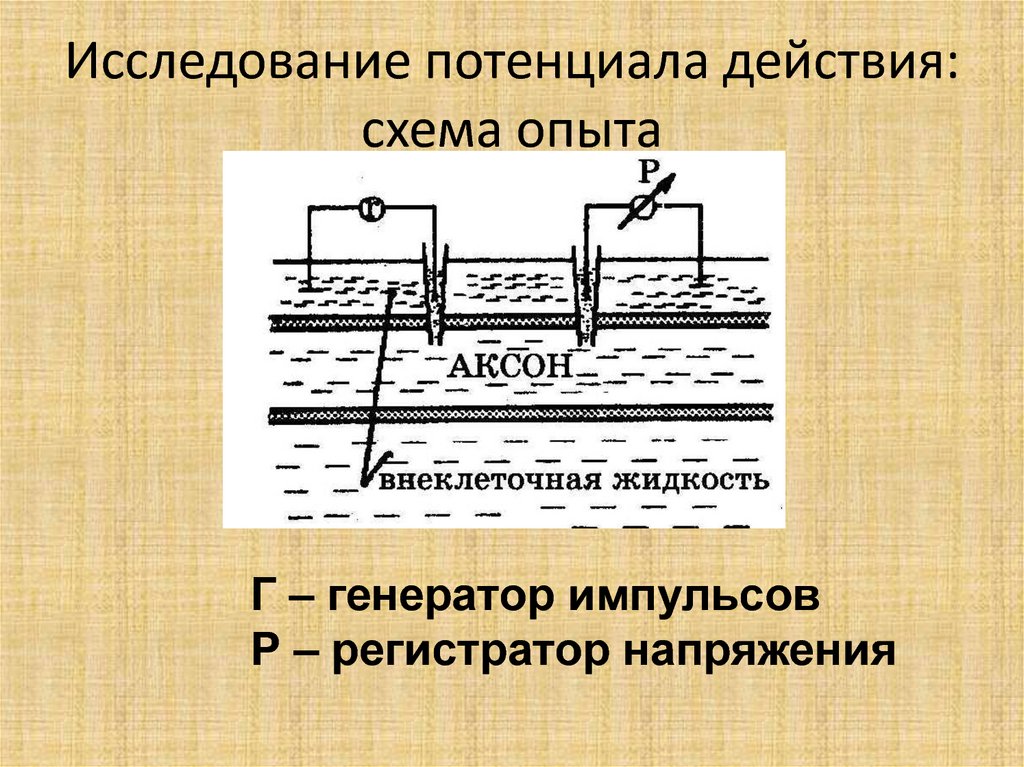
38. Исследование потенциала действия: схема опыта
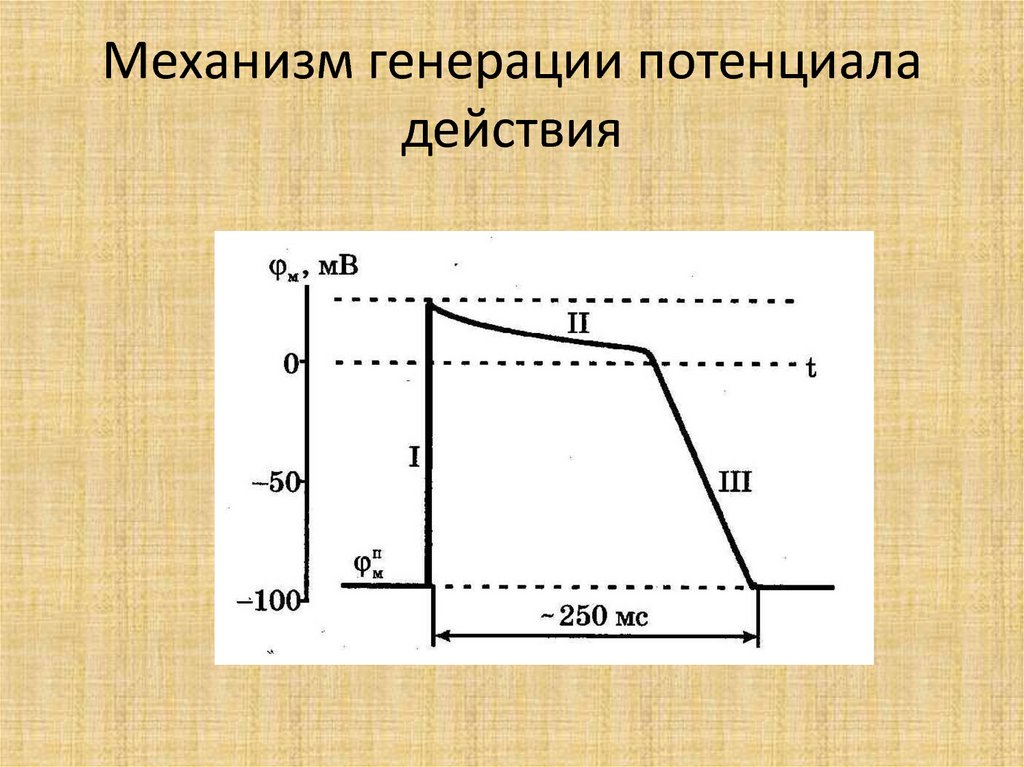
Г – генератор импульсовР – регистратор напряжения
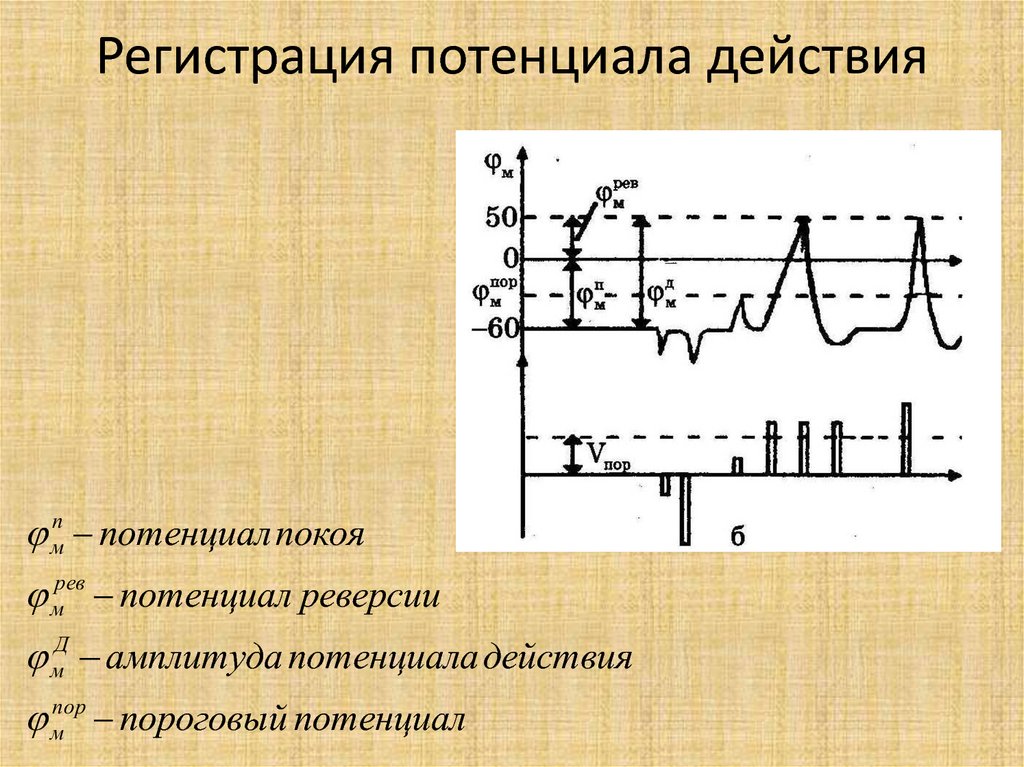
39. Регистрация потенциала действия
мп потенциал покоямрев потенциал реверсии
мД амплитуда потенциала действия
мпор пороговый потенциал
40. Потенциал действия – ПД – не зависит от амплитуды деполяризующего потенциала
Дм
п
м
рев
м
мп потенциал покоя
мрев потенциал реверсии
мД амплитуда потенциала действия
41. Свойства ПД
1. Наличие порогового значениядеполяризующего потенциала
2. Закон «все или ничего»
3. Период рефрактерности
4. Резкое снижение сопротивления БМ в
момент возбуждения (покой: 0,1 Ом*м2,
возбуждение: 0,0025 Ом*м2)
42. Положительный потенциал реверсии имеет Na природу
RT PK K i PNa Na i PCl Cl oм
ln
F
PK K o PK Na o PK Cl i
RT Cвнут
м
ln
ZF Cнар
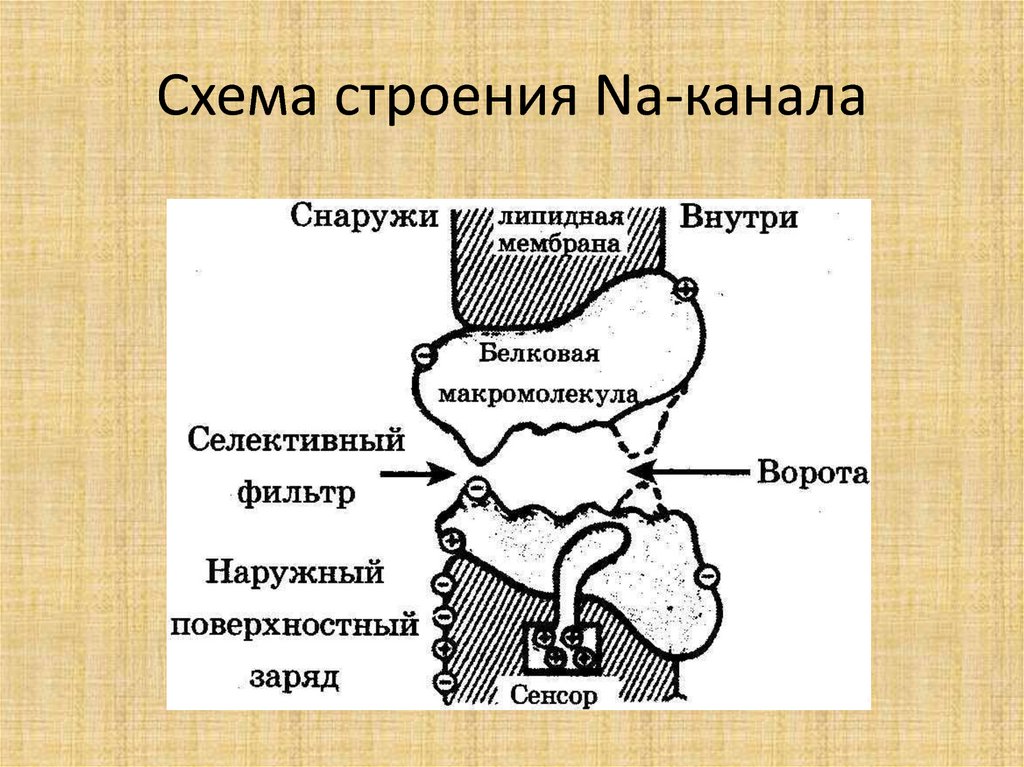
43. Проницаемость БМ
• В состоянии покоя:РК : РNa : РCl = 1 : 0,04 : 0,45
• В состоянии возбуждения:
РК : РNa : РCl = 1 : 20 : 0,45
44. Уравнение Ходжкина-Хаксли
d мI м См
Ii
dt
I м ток через мембрану
С м емкость мембраны
I
i
сумма ионных токов через мембрану
d м
I м См
I K I Na I ут
dt
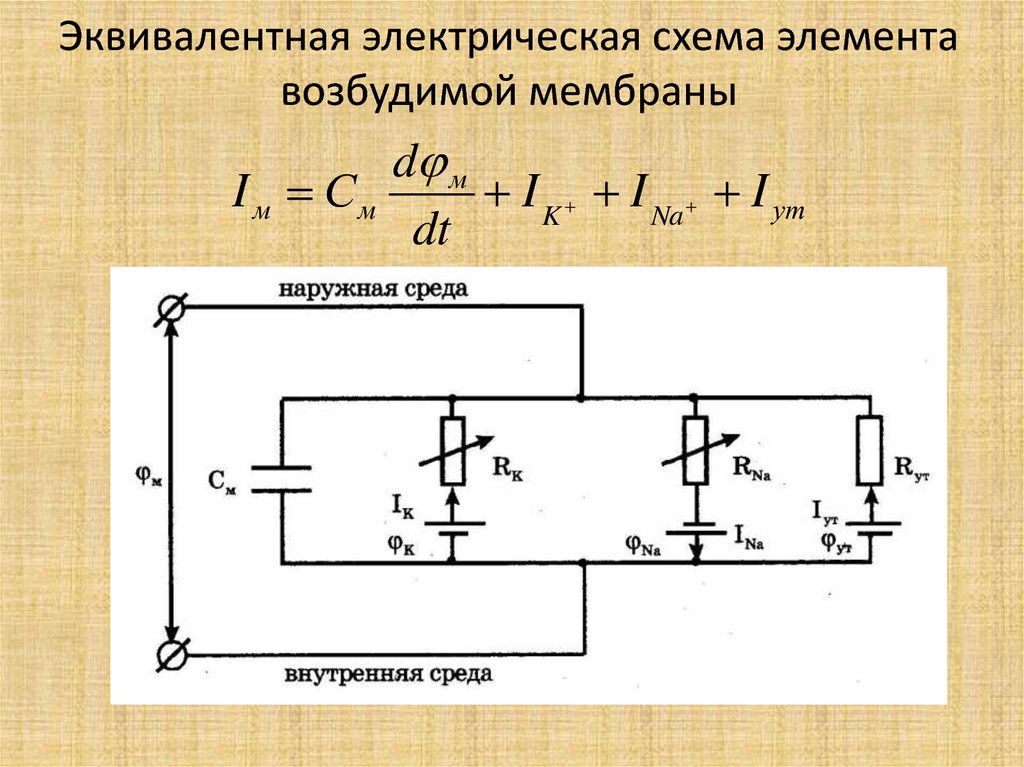
45. Эквивалентная электрическая схема элемента возбудимой мембраны
d мI м См
I K I Na I ут
dt
46. Т. Х-Х: Возбуждение элемента мембраны связано с изменением проводимости мембраны для ионов натрия и калия
I i g i ( м i )p
1
g i проводимость мембраны
Ri
d м
р
р
I м См
g K ( м Кр ) g Na ( м Na
) g ут ( м ут
)
dt
Т. Х-Х: Возбуждение элемента мембраны связано с
изменением проводимости мембраны для ионов
натрия и калия
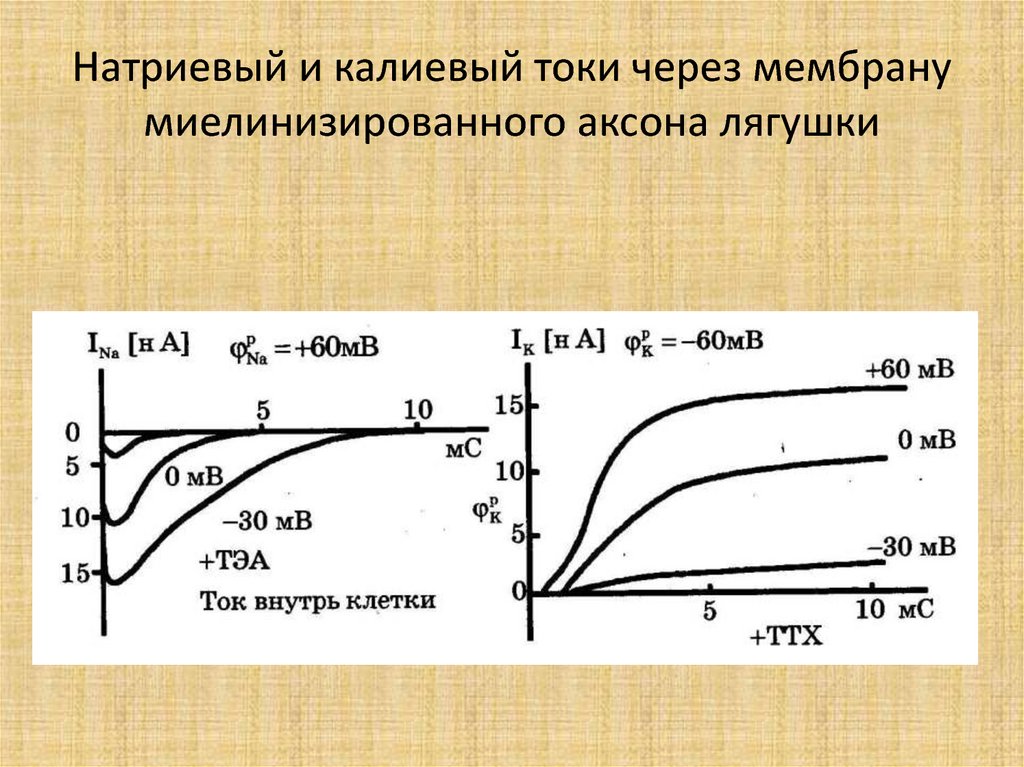
47. Опыты с фиксацией напряжения
м в н нар1. избавиться от емкостных токов
См d м dt
2. исключить изменение ионных
проводимостей натрия и калия при
изменении мембранного потенциала и
изучить их изменение в различные фазы
развития возбуждения
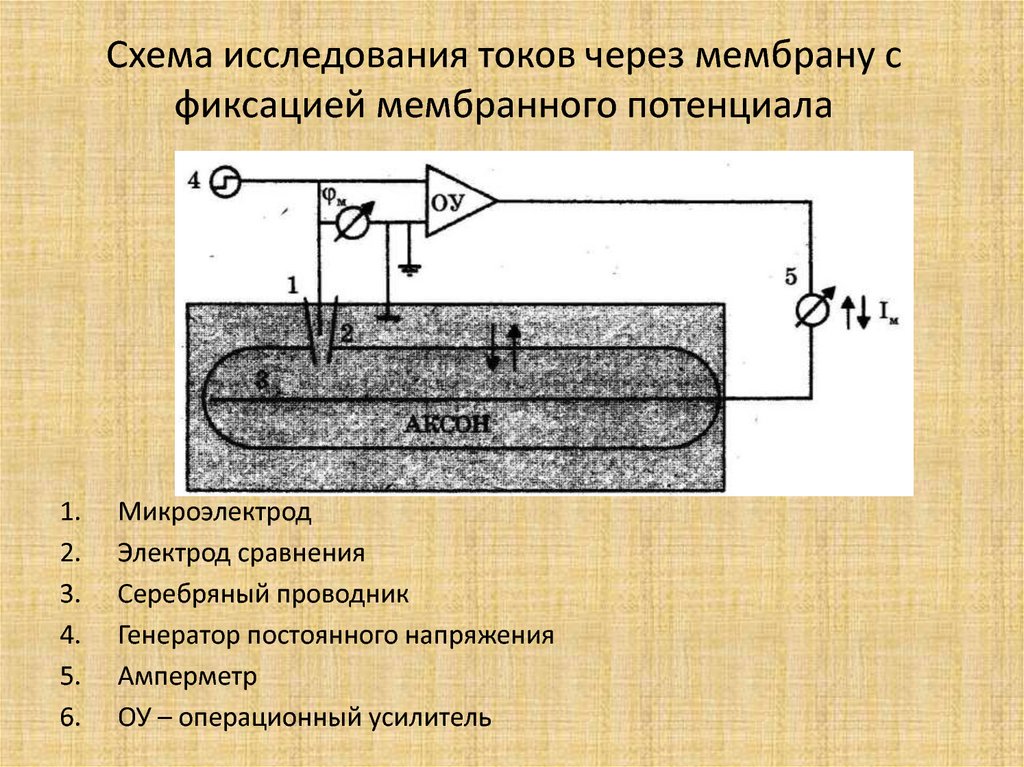
48. Схема исследования токов через мембрану с фиксацией мембранного потенциала
1.2.
3.
4.
5.
6.
Микроэлектрод
Электрод сравнения
Серебряный проводник
Генератор постоянного напряжения
Амперметр
ОУ – операционный усилитель
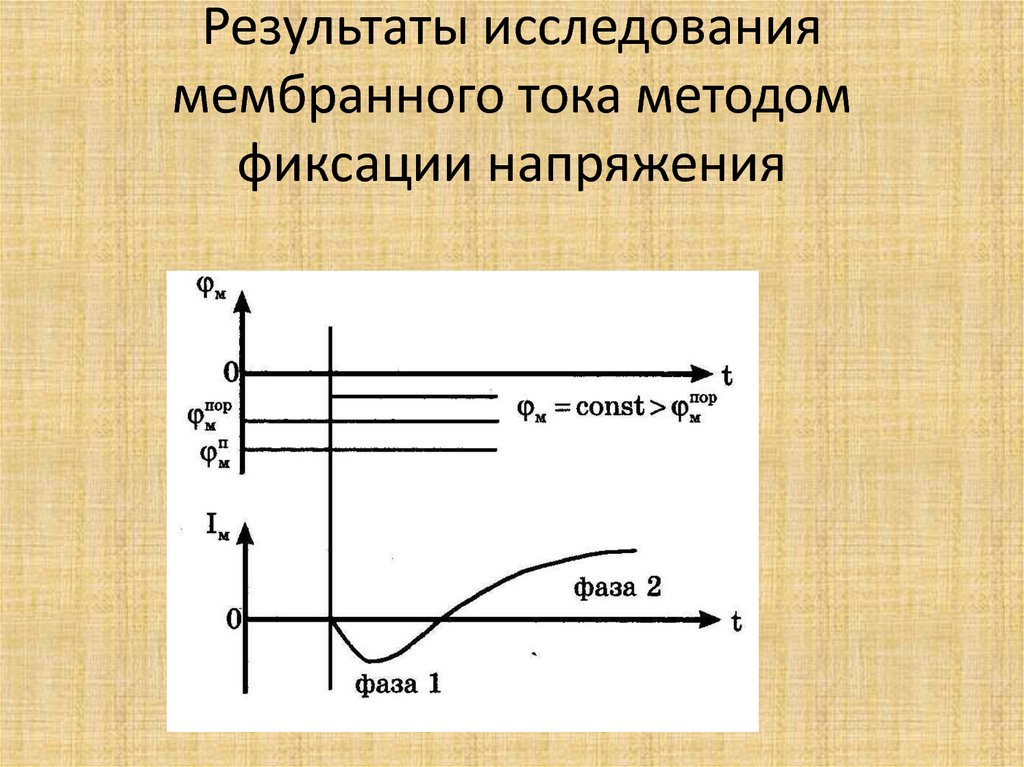
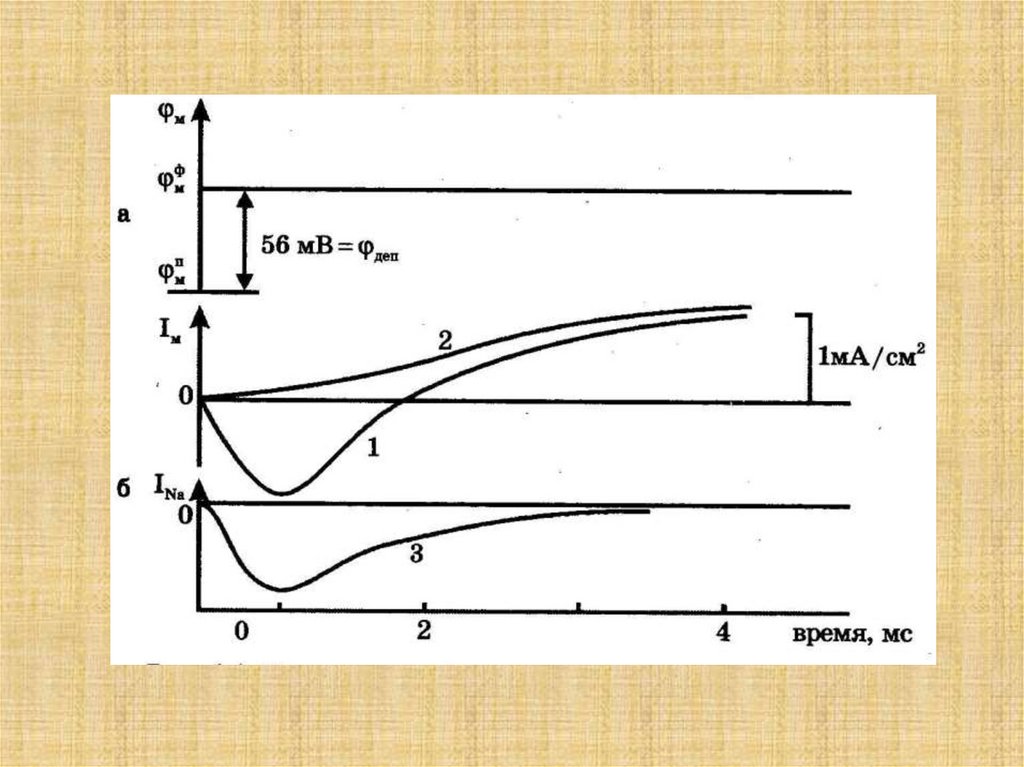
49. Результаты исследования мембранного тока методом фиксации напряжения
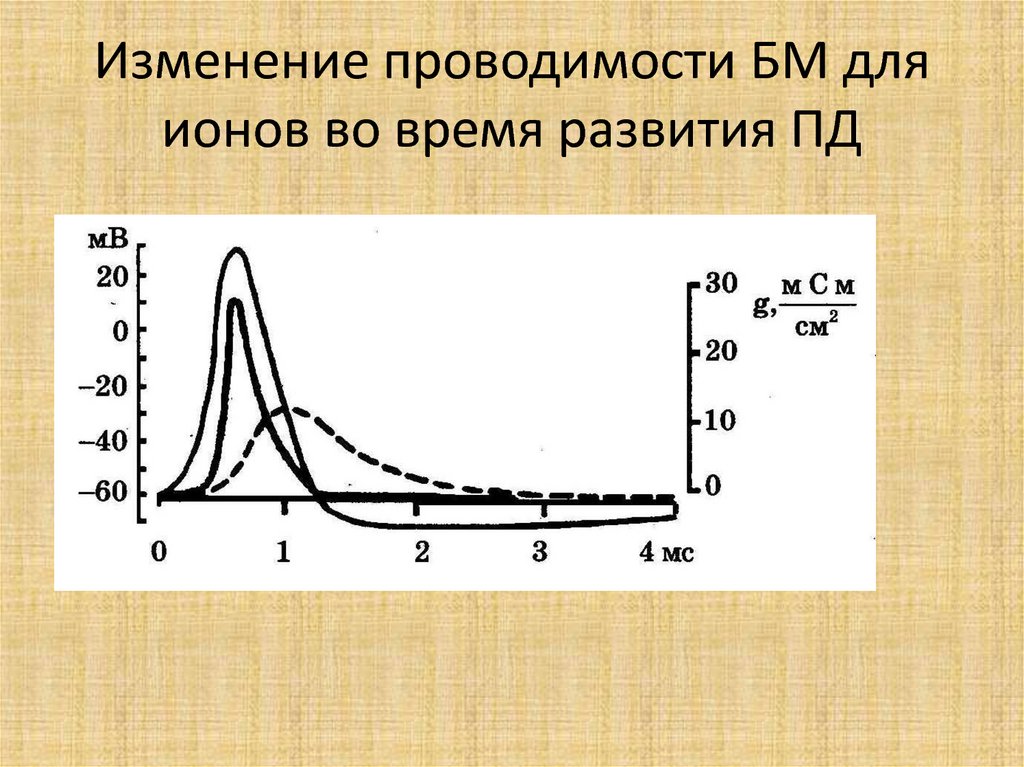
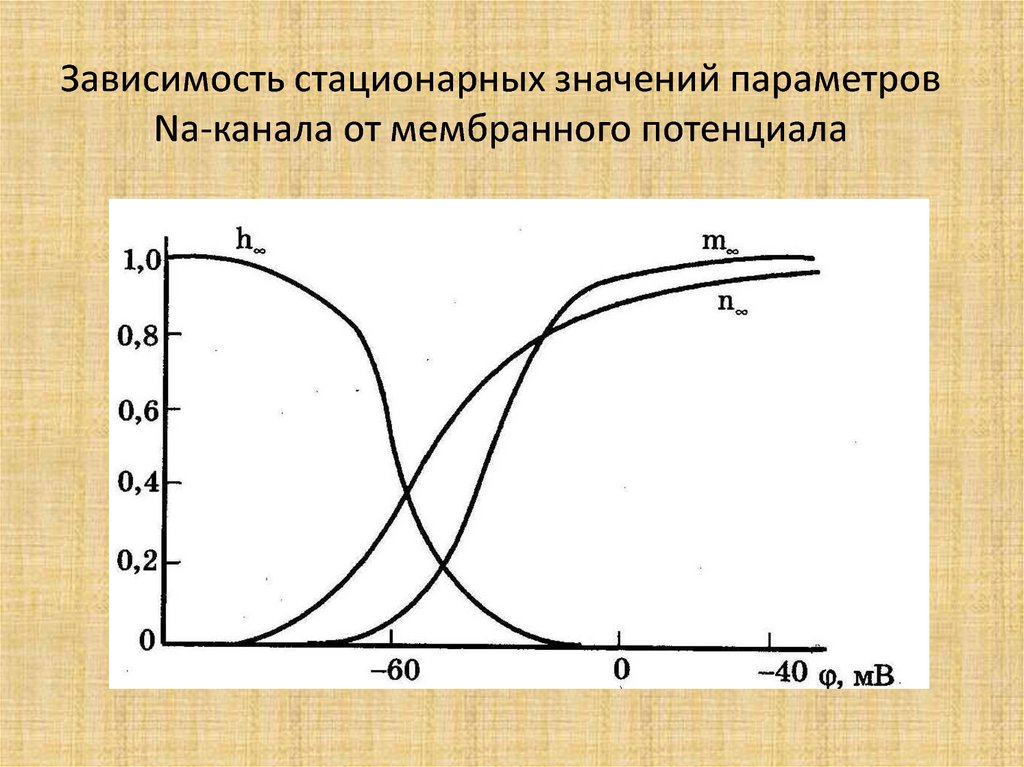
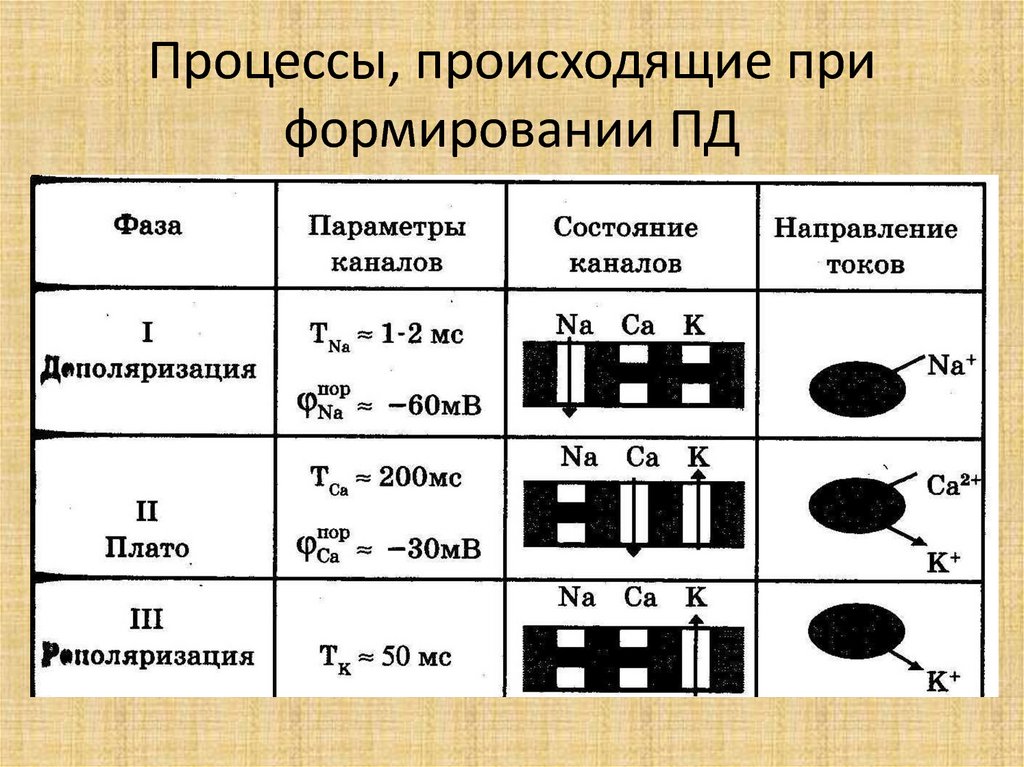
50. Изменение проводимости БМ для ионов во время развития ПД
51. Распространение нервного импульса вдоль возбудимого волокна
Возбудимость – способность клеток кбыстрому ответу на раздражение, который
проявляется через совокупность физических,
физико-химических процессов и
функциональных изменений.
Нервная, мышечная, железистая
Признак возбуждения: изменение
электрического состояния клеточной
мембраны: возбужденный участок клетки –
электроотрицателен по отношению к
невозбужденному участку
52. Потенциал действия
• Общее изменение разности потенциаловмежду клеткой и средой, происходящее
при пороговом и сверхпороговом
возбуждении клеток
- Обеспечивает проведение возбуждения по
нервным волокнам
- Индуцирует процессы мышечного
сокращения
- Индуцирует секрецию железистых клеток
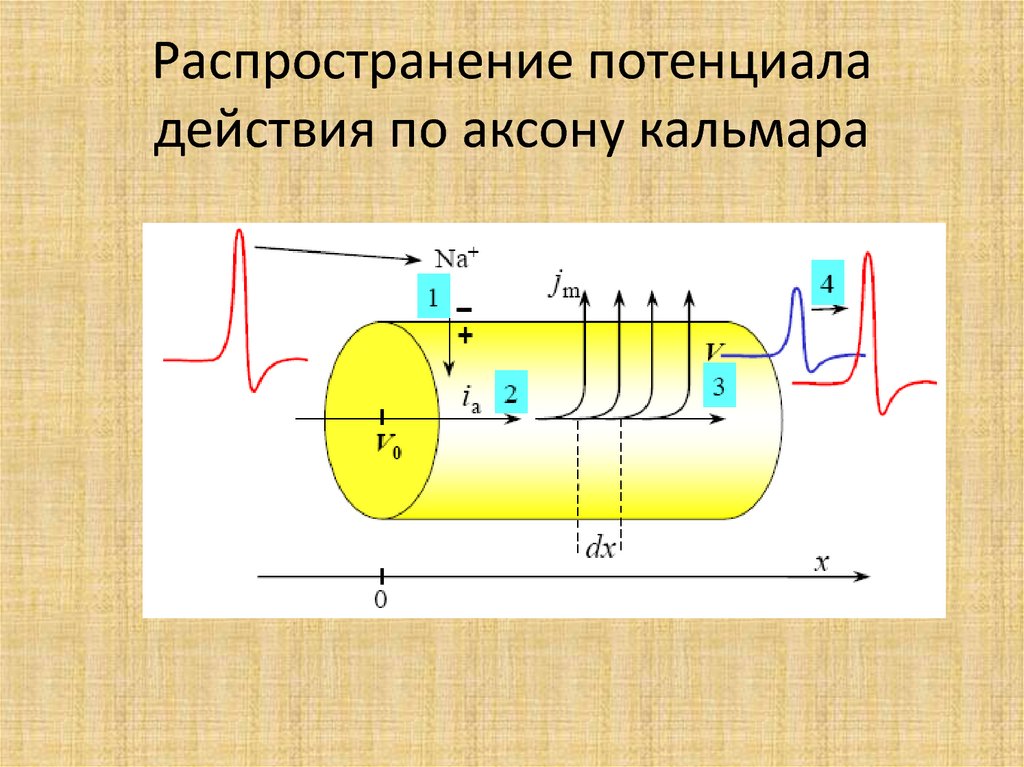
53. Распространение потенциала действия по аксону кальмара
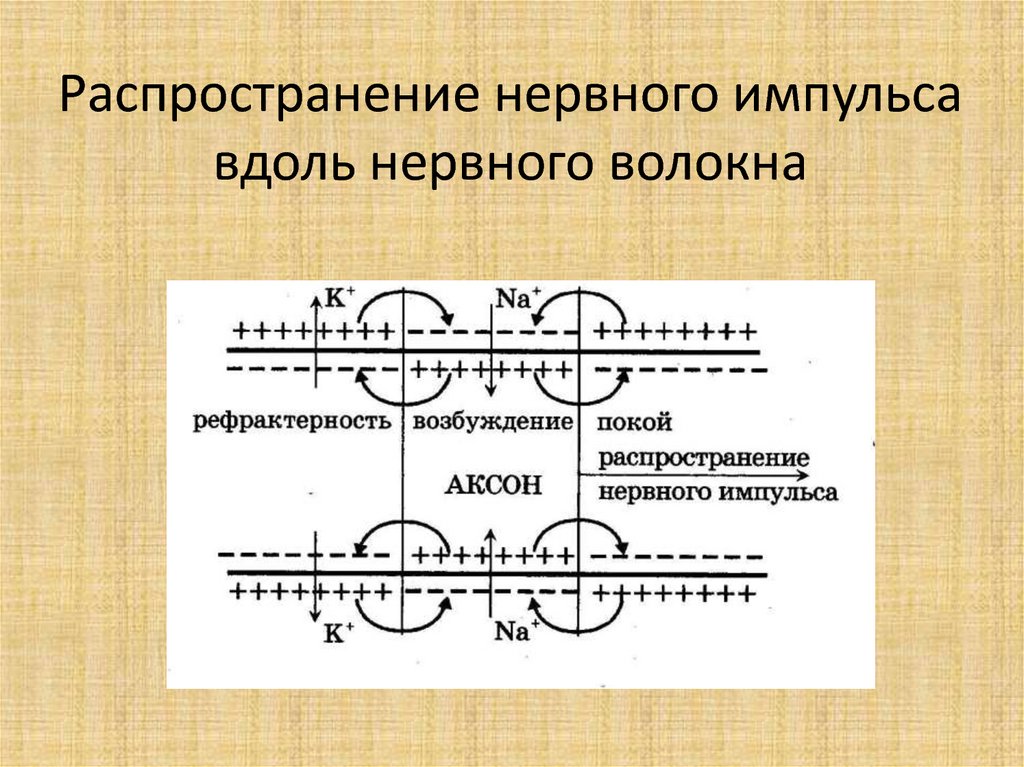
54. Распространение нервного импульса вдоль нервного волокна
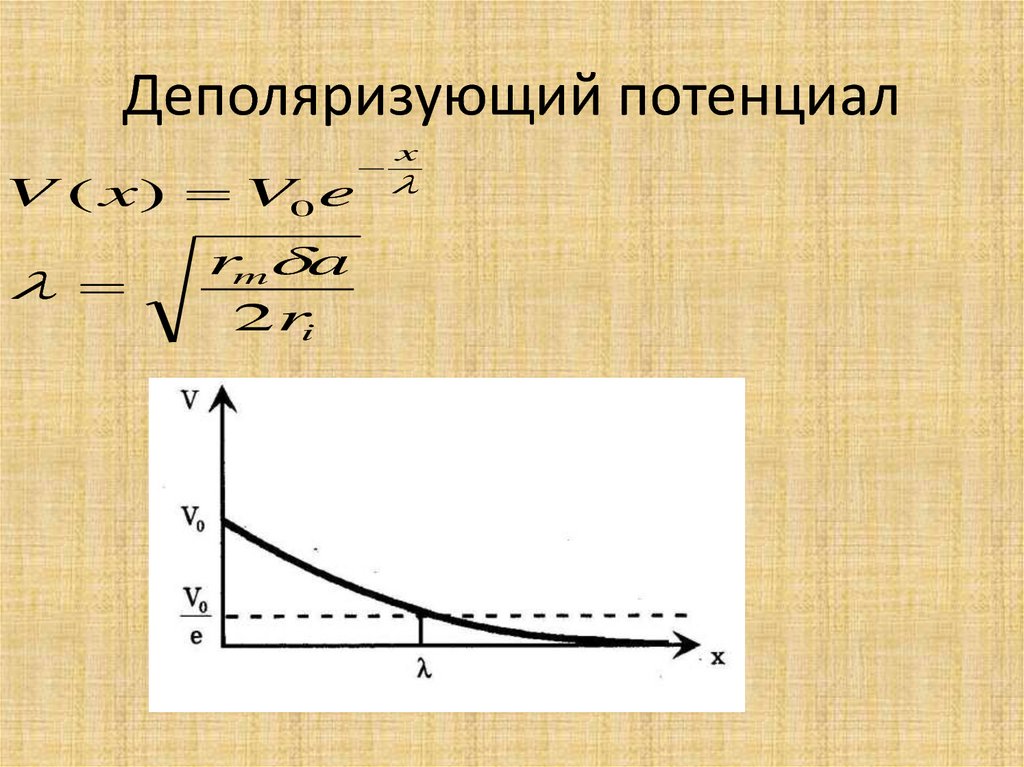
55. Деполяризующий потенциал
V ( x ) V0 erm a
2ri
x



















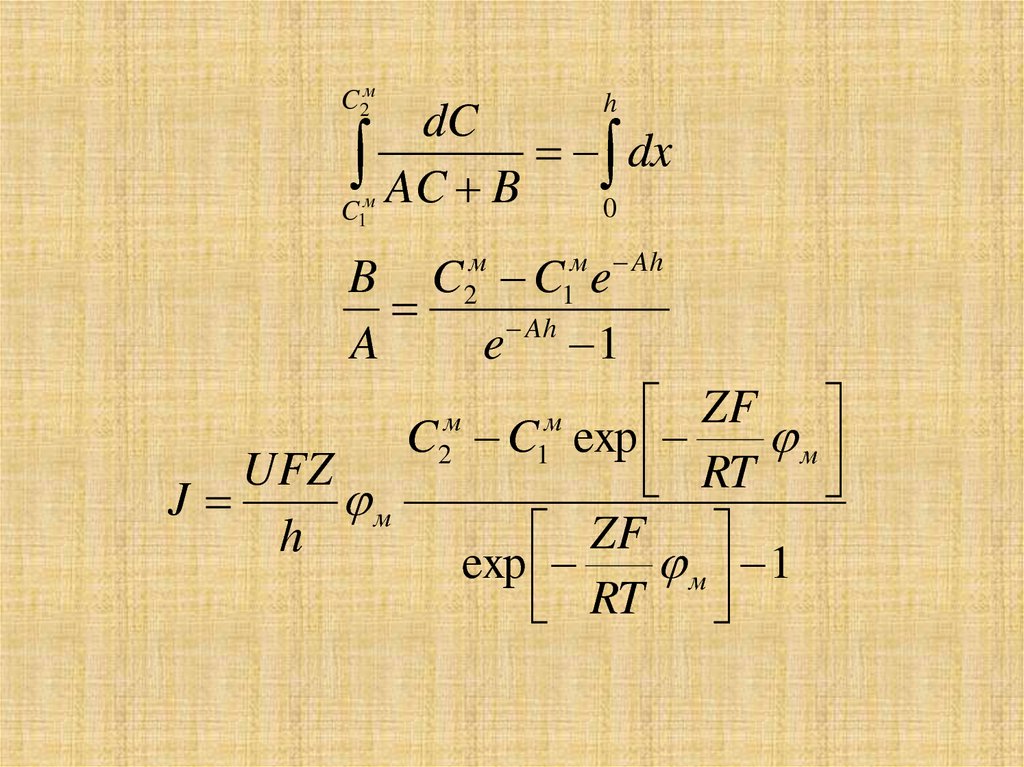





















 biology
biology








