Similar presentations:
Преобразование рациональных выражений
1.
26.06.20111
2.
Изучить правила преобразованиярациональных выражений;
Научиться упрощать выражения;
Научиться доказывать тождества.
26.06.2011
2
3.
Рациональное число можно представитьв виде
P
Q
, где P – целое число,
Q – натуральное число.
Рациональные числа - все целые числа и все
дроби, как положительные так и отрицательные.
Рациональное выражение – алгебраическое
выражение составленное из чисел и переменных
с помощью арифметических операций и возведения
в натуральную степень.
Дробное выражение – это алгебраическая дробь.
Целое выражение - выражение представленное в
виде многочлена .
26.06.2011
3
4.
Для преобразования рациональных выраженийпринят тот же порядок действий, что и для
преобразования числовых выражений.
Это значит, что сначала выполняют действия
в скобках, затем действия второй ступени
(умножение, деление, возведение в степень),
а затем действия первой ступени
(сложение, вычитание).
Рассмотрим наиболее сложные задания:
26.06.2011
4
5.
Рассмотрим пример 1.Упростить выражение.
a
с
a
с
1 1
1 1
( ) : ( c a ) ca ( )
c a
c a
a c
a c
(
) : ( c a ) ca (
)
c a
c a
a c
1
a c
(
)(
) ca (
)
c a c a
c a
1
1
(a c )
a c
( a c ).
ca (
)
c a (c a )
c a 1 c a
1
1
26.06.2011
5
6.
Рассмотрим пример 2.Упростить выражение:
a2
a3
a
a2
a )(
2
):(
2
)
2
2
a b a 2ab b
a b a b
Решение
Для упрощения выражения выбираем способ преобразования
по действиям.
a+b
1
2
3
2
3
a
a
a
a
1)
2
2
2
a b a 2ab b
a b (a b)
a (a b ) a
a a b a
a b
.
2
2
2
(a b)
(a b)
(a b)
2
26.06.2011
3
3
2
3
2
6
7.
a-b1
2
a
a
a
a2
2)
2
2
a b a b
a b ( a b )( a b )
ab
a( a b ) a 2
a 2 ab a 2
.
( a b )( a b ) ( a b )( a b ) ( a b )( a b )
1
1
2
a 2b
ab
a b( a b )( a b )
3)
:
2
2
( a b ) ( a b )( a b )
(a b ) a b
1
1
a( a b )
a( b a )
.
(a b)
a b
26.06.2011
7
8.
Рассмотрим пример 3.Упростить выражение:
z 2
z
z 4
2
б) 2
:(
2
2
)
4 z 16 z 16 2 z 4 2 z 8 z 2 z
2
Решение
Для упрощения выражения выбираем способ преобразования
цепочкой.
z 2
z
z 4
2
2
:(
)
2
4 z 16 z 16 2( z 2 ) 2( z 4 ) z( z 2 )
2
z 2
z
z 4
2
:(
)
2
2
4( z 4 z 4 ) 2( z 2 ) 2( z 4 ) z( z 2 )
2
26.06.2011
8
9.
Z(Z + 2)z
2(z – 2)
z 2
z
z 4
2
:(
)
2
2
4( z 2 )
2( z 2 ) 2( z 4 ) z( z 2 )
2
z 2
z 2 ( z 2 ) z( z 2 4 ) 4( z 2 )
:(
)
2
2
4( z 2 )
2 z( z 4 )
z 2
z 3 2z 2 z 3 4z 4z 8
:(
)
2
2
4( z 2 )
2 z( z 4 )
z 2
2z 8z 8
:(
)
2
2
4( z 2 )
2 z( z 4 )
2
26.06.2011
9
10.
z 22( z 4 z 4 )
:(
)
2
2
4( z 2 )
2 z( z 4 )
2
1
z 2
2( z 2 )
:(
)
2
2
4( z 2 ) 1 2 z( z 4 )
2
z 2
z( z 2 4 )
(
)
2
2
4( z 2 )
(z 2)
1
1
1
z
( z 2 )( z 2 )( z 2 )z
.
2
2
4( z 2 )
4( z 2 ) ( z 2 )
1
26.06.2011
10
11.
Доказать тождество – это значит установить,что при всех допустимых значениях переменной
его левая и правая части тождественно равные
выражения.
Способы доказательства тождеств:
1) Преобразовывают левую часть и получают в итоге
правую часть;
2)Преобразовывают правую часть и получают в итоге
левую часть;
3)По отдельности преобразовывают правую, а затем
левую часть и в итоге получают равные выражения;
4) Составляют разность левой и правой части и
в итоге получают нуль.
Какой способ выбрать – зависит от конкретного
вида тождества, которое предлагают доказать.
26.06.2011
11
12.
Рассмотрим пример 4.Доказать тождество.
y 2 10 y 25 3
y 5 3
(
) :(
) 8.
2
y 25
2 y 10
Решение
Для доказательства тождества выбираем первый способ:
преобразуем левую часть.
y 2 10 y 25 3
y 5 3
(
) :(
)
2
y 25
2 y 10
( y 5 )2
2 y 10 3
3
(
) (
)
( y 5 )( y 5 )
y 5
( y 5 )2
2( y 5 ) 3
3
(
) (
)
( y 1 5 )( y 5 )
y 5
26.06.2011
.
12
13.
( y 5 ) 3 2( y 5 ) 3(
) (
)
( y 5)
y 5
3
3
( y 5 ) 8( y 5 )
3
3
( y 5) ( y 5)
1
8( y 5 ) ( y 5 )
8.
3
3
( y 5) ( y 5)
1
3
1
3
1
И так, 8 = 8.
Тождество справедливо лишь для допустимых
значений переменной у.
26.06.2011
13
14.
1. Какие числа называются рациональными?2. Какое выражение называется дробным?
3. Какое выражение называется
рациональным?
4. Что значит доказать тождество?
5. Какие способы доказательства тождества
можно назвать?
26.06.2011
14








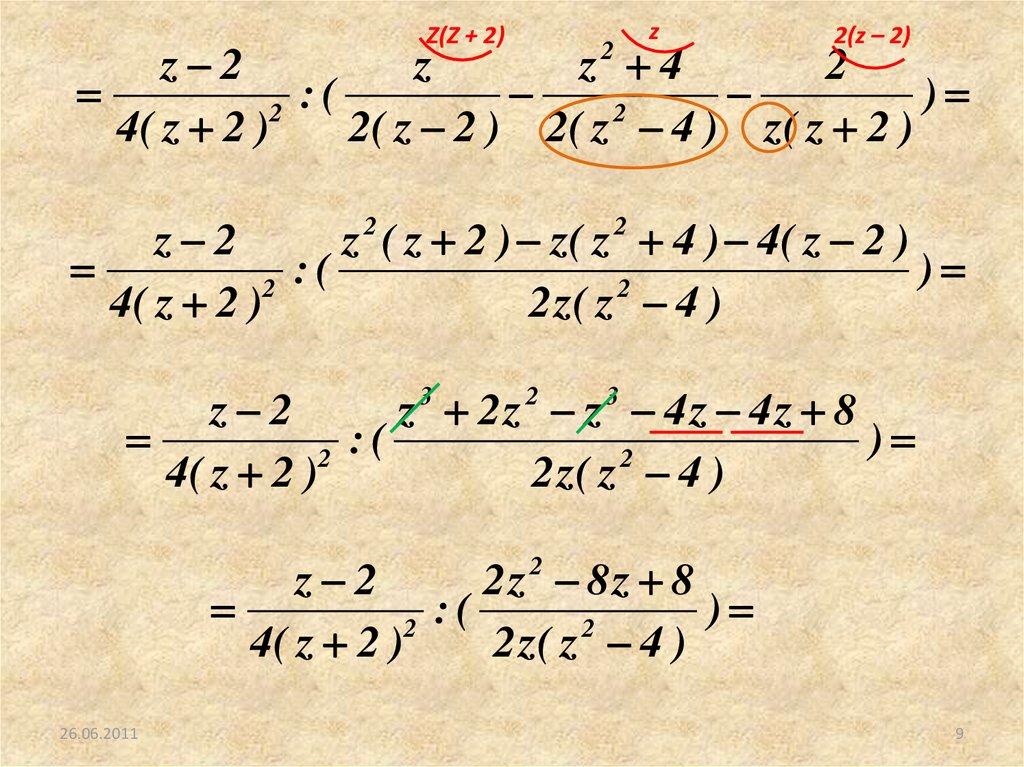
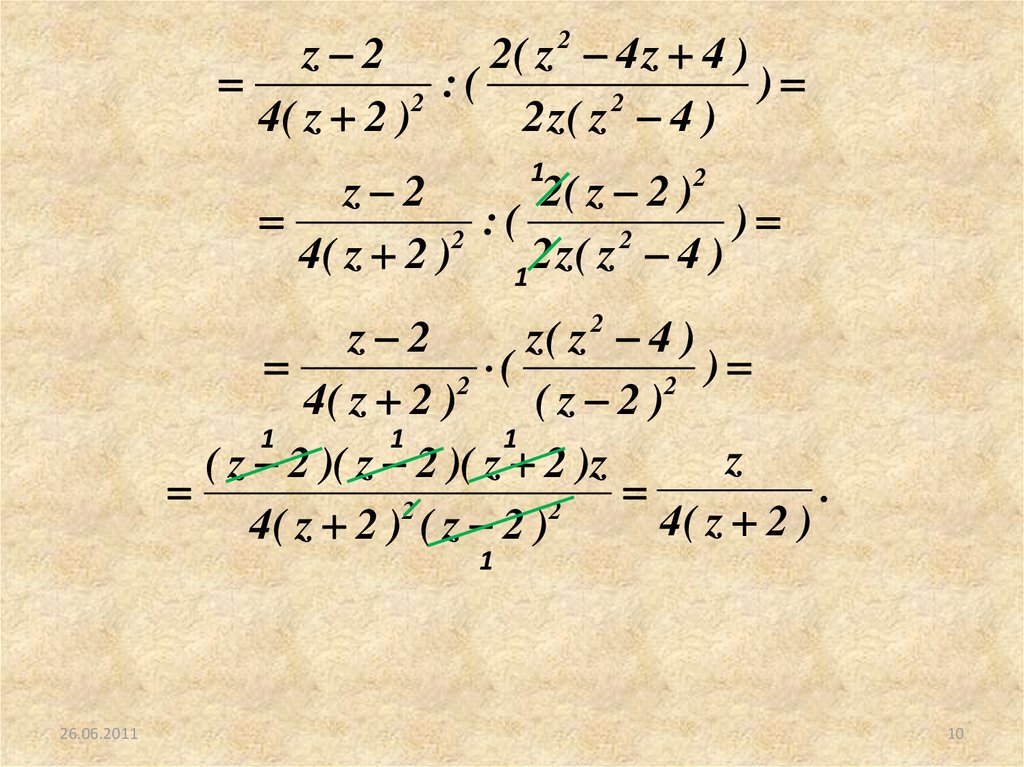




 mathematics
mathematics








