Similar presentations:
Детали машин и основы конструирования
1.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮМОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ
В.Г. Клоков
ДЕТАЛИ МАШИН
И ОСНОВЫ КОНСТРУИРОВАНИЯ
Конспект лекций
Москва
2008
2.
Рецензенты:Никифоров Н.И., доктор технических наук, заслуженный
машиностроитель, генеральный директор ОАО «ВНИИавтогенмаш»;
Патрахальцев Н.Н., доктор технических наук, заслуженный
работник высшей школы РФ, профессор кафедры теплотехники
и тепловых двигателей Российского университета дружбы народов
Клоков В.Г.
Детали машин и основы конструирования. Конспект
лекций
2
3.
ОглавлениеОсновные условные обозначения .................................................................6
Введение......................................................................................................... 8
ЧАСТЬ I. ЗУБЧАТЫЕ И ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
Глава 1. ВВЕДЕНИЕ В ПЕРЕДАЧИ .......................................................... 10
1.1. Краткая классификация механических передач вращения ......... 10
1.2. О контактных напряжениях .......................................................... 12
Глава 2. ЗУБЧАТЫЕ ПЕРЕДАЧИ .............................................................. 16
2.1. Общие сведения ............................................................................ 16
2.2. Виды зубчатых передач ................................................................ 18
Глава 3. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ ........................ 20
3.1. Расчет цилиндрических зубчатых передач на контактные
напряжения ................................................................................... 20
3.2. Определение модуля и числа зубьев шестерни и колеса ............ 23
3.3. Корректирующие коэффициенты нагрузки ................................. 28
3.4. Допускаемые контактные напряжения при расчете
цилиндрических зубчатых передач ............................................. 31
3.5. Расчет зубчатых передач по прочности зубьев на изгиб ............ 35
3.6. Допускаемые напряжения изгиба для цилиндрических
зубчатых передач .......................................................................... 40
3.7. Расчет цилиндрических зубчатых передач
на кратковременную перегрузку (т.е. на отсутствие
пластических деформаций или хрупкого разрушения) .............. 41
3.8. Особенности расчета открытых цилиндрических
зубчатых передач .......................................................................... 42
3.9. Степени точности цилиндрических зубчатых колес ................... 43
3.10. Силы в зацеплении и воздействия на валы
в цилиндрических зубчатых передачах ..................................... 44
3.11. Смазывание зубчатых передач ................................................... 47
Глава 4. КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ ................................... 50
4.1. Общие сведения ............................................................................ 50
4.2. Расчет конических зубчатых передач с круговыми зубьями
и с n = 35° на контактные напряжения ........................................ 53
4.3. Проверочный расчет конических передач
с круговыми зубьями на контактные напряжения ...................... 56
4.4. Определение допускаемых контактных напряжений ................. 56
4.5. Расчет конических зубчатых передач
с круговыми зубьями на изгиб ................................................... 57
4.6. Допускаемые напряжения изгиба для конических
зубчатых передач ......................................................................... 58
3
4.
4.7. Расчет конических зубчатых передачна кратковременную перегрузку ................................................. 58
4.8. Силы в зацеплении конических передач
с круговыми зубьями .................................................................... 59
Глава 5. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ ........................................................... 60
5.1. Общие сведения и кинематика ..................................................... 60
5.2. Расчет червячных передач на контактные напряжения .............. 65
5.3. Допускаемые контактные напряжения
при расчете червячных передач ................................................... 66
5.4. Расчет червячных передач на изгиб ............................................. 68
5.5. Допускаемые напряжения изгиба для червячных колес ............. 69
5.6. Проверка червячной передачи на нагрев ..................................... 70
ЧАСТЬ II. ВАЛЫ. ПОДШИПНИКИ. МУФТЫ
Глава 6. ВАЛЫ............................................................................................. 71
6.1. Общие сведения ............................................................................ 71
6.2. Расчет валов на статическую прочность ...................................... 73
6.3. Расчет валов на усталостную выносливость ............................... 74
6.4. Расчет валов на жесткость ............................................................ 76
Глава 7. ПОДШИПНИКИ ........................................................................... 77
7.1. Общие сведения ............................................................................ 77
7.2. Достоинства и недостатки подшипников качения
в сравнении с подшипниками скольжения ................................. 79
7.3. Основные типы подшипников качения и их характеристики .... 80
7.4. Условные обозначения подшипников качения ........................... 84
7.5. Основные критерии работоспособности и расчета
подшипников качения .................................................................. 85
7.6. Расчет подшипников качения на долговечность ......................... 86
7.7. Определение эквивалентной нагрузки ......................................... 88
7.8. Материалы, применяемые для изготовления подшипников
качения .......................................................................................... 90
7.9. Смазка подшипников качения ...................................................... 90
7.10. Посадки подшипников качения .................................................. 91
Глава 8. МУФТЫ ......................................................................................... 92
8.1. Классификация механических муфт ............................................ 93
8.2. Расчет муфты упругой втулочно-пальцевой ............................... 96
8.3. Расчет предохранительной муфты со срезным штифтом ........... 97
ЧАСТЬ III. РЕМЕННЫЕ И ЦЕПНЫЕ ПЕРЕДАЧИ
Глава 9. РЕМЕННЫЕ ПЕРЕДАЧИ ............................................................. 99
9.1. Общие сведения ............................................................................ 99
9.2. Классификация ременных передач по способам
натяжения ремня ......................................................................... 101
4
5.
9.3. Преимущества и недостатки ременных передачпо сравнению с зубчатыми......................................................... 102
9.4. Силы в ременной передаче и напряжения в ремне ................... 103
9.5. Нагрузка на валы и подшипники ................................................ 104
9.6. Напряжения в ремне.................................................................... 104
9.7. Тяговая способность и расчет ременных передач
КПД ременных передач.............................................................. 106
9.8. Расчет и проектирование клиноременных передач .................. 109
Глава 10. РАСЧЕТ И ПРОЕКТИРОВАНИЕ ЦЕПНЫХ ПЕРЕДАЧ ...... 117
10.1. Общие сведения ........................................................................ 117
10.2. Расчет и проектирование цепных передач
с роликовой цепью ............................................................................. 119
ЧАСТЬ IV. СОЕДИНЕНИЯ
Глава 11. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ .................. 126
11.1. Шпоночные соединения и их расчет ........................................ 126
11.2. Шлицевые соединения и их расчет .......................................... 129
Глава 12. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ .................................................. 131
12.1. Резьбы. Общие сведения ........................................................... 131
12.2. Обозначение болтовых соединений ......................................... 136
12.3. Расчет незатянутых винтов ....................................................... 137
12.4. Материалы для изготовления деталей резьбовых
соединений и допускаемые напряжения ................................ 140
12.5. Расчет резьбы на прочность...................................................... 141
12.6. Усилия и моменты, действующие в резьбовых соединениях
при затяжке ............................................................................... 144
12.7. Основные случаи расчета резьбовых соединений ................... 149
Глава 13. СВАРНЫЕ СОЕДИНЕНИЯ ...................................................... 158
13.1. Общие сведения ........................................................................ 158
13.2. Сварные соединения стыковыми швами ................................. 160
13.3. Сварные соединения угловыми швами .................................... 161
13.4. Допускаемые напряжения для расчета сварных соединений . 163
13.5. Примеры расчетов сварных соединений.................................. 165
Глава 14. ЗАКЛЕПОЧНЫЕ СОЕДИНЕНИЯ ........................................... 169
14.1. Общие сведения ........................................................................ 169
14.2. Расчет заклепки на прочность .................................................. 171
Список литературы .................................................................................... 173
5
6.
Основные условные обозначенияFп – сила нормального давления
Fa – осевая сила
Ft – окружная сила
Fr – радиальная сила
Fм – нагрузка от муфты
Т – вращающий момент на валу
Мизг и Мкр – изгибающий и крутящий моменты
в и в – пределы прочности материала
1 и 1 – пределы выносливости материала
т и т – пределы текучести материала
[ ]Н и [ ]F – допускаемые напряжения при расчете на контактные напряжения
S – коэффициент безопасности (коэффициент запаса прочности)
Sн – коэффициент безопасности при расчете на контактные
напряжения и изгиб
SF – коэффициент безопасности при расчете на изгиб
Hlim – предел контактной выносливости
Flim – предел выносливости зубьев по напряжениям изгиба
NH и NF – число циклов нагружения при расчете на контактную
прочность и изгиб
NHЕ и NFЕ – эквивалентное число циклов нагружения при расчете на контактную прочность и изгиб
NHG и NFG – базовое число циклов нагружения при расчете на
контактную прочность и изгиб
аw и а – межосевые расстояния
l – длина
А – площадь сечения
т, тп, тt – модули зубчатого зацепления
D, d – диаметры
b, bw – ширина зубчатого венца
bа, bd – коэффициенты ширины зуба
– угол наклона зуба
α, αw = 20 – углы зацепления
6
7.
Re – внешнее делительное конусное расстояние коническойпередачи
α – коэффициент торцового перекрытия
Z – число зубьев зубчатого колеса или звездочки цепной передачи (или число ремней в ременной передаче)
КН, КF – коэффициенты нагрузки
КНβ, КFβ – коэффициенты концентрации нагрузки по длине контактных линий
КНα, КFα – коэффициенты неравномерности распределения нагрузки между зубьями, одновременно находящимися
в зацеплении
Yβ,YFβ – коэффициенты повышения прочности косозубых и
шевронных передач при расчете на изгиб
КНV, КFV – коэффициенты динамической нагрузки
YF – коэффициент формы зуба
Рц – шаг цепи
Р – мощность
рц – давление в шарнире цепи
п – частота вращения
U – передаточное число
η – КПД
НВ, НRС – твердость
tE, ТЕ – эквивалентное время работы
Т пуск
Кпуск =
– коэффициент пусковой перегрузки
Т
С, Со – динамическая и статическая грузоподъемность подшипников
РЕ – эквивалентная динамическая нагрузка на подшипник
L, Lh – долговечность подшипников
7
8.
ВВЕДЕНИЕКурс «Детали машин» является первым из расчетноконструкторских курсов, в которых изучаются основы расчета и
проектирования как отдельных деталей, так и машин или механизмов в целом.
Особенности курса «Детали машин»:
– расчет реальных деталей;
– многозначность решений;
– связь с проектированием и технологией изготовления.
Существуют два метода расчета:
1. Проектный – дана лишь схема конструкции, ее назначение и условия работы. Требуется определить (рассчитать) необходимые размеры, выбрав допускаемые напряжения в зависимости от принятых материалов конструкции.
Проектный расчет является упрощенным.
2. Проверочный – даны все размеры и материалы деталей
конструкции, а также ее назначение. Требуется:
1) либо определить рабочие напряжения, возникающие в
конструкции (если дана нагрузка – усилие, момент, мощность),
и сравнить их с допускаемыми;
2) либо определить допускаемую нагрузку, выбрав (рассчитав) допускаемое напряжение.
Проверочный расчет является уточненным.
Основными критериями работоспособности и расчета деталей машин являются прочность, жесткость, износостойкость,
теплостойкость, виброустойчивость, надежность.
1. Прочность – главный критерий работоспособности для
большинства деталей. Основы расчетов на прочность изучают в
курсе «Сопротивление материалов». В курсе «Детали машин»
общие методы расчетов на прочность рассматривают в приложении к конкретным деталям и придают им форму инженерных
расчетов.
2. Жесткость – способность детали сопротивляться изменению формы и размеров под нагрузкой.
8
9.
3. Износостойкость – свойство материала оказывать сопротивление изнашиванию.4. Теплостойкость – способность конструкции работать в
течение заданного срока в пределах заданных температур.
5. Виброустойчивость – способность конструкции работать в заданном диапазоне режимов без недопустимых колебаний.
6. Надежность – вероятность безотказной работы в течение заданного срока в определенных условиях.
9
10.
ЧАСТЬ I. ЗУБЧАТЫЕ И ЧЕРВЯЧНЫЕ ПЕРЕДАЧИГлава 1. ВВЕДЕНИЕ В ПЕРЕДАЧИ
Механические передачи (зубчатые, червячные, ременные
и др.) служат для передачи энергии и трансформации (преобразования) движения.
Существуют два вида передач:
– силовые передачи – для передачи мощности;
– распределительные – для изменения частоты вращения.
Применение передач обусловлено разницей в частоте вращения двигателей (п1), в частности, электродвигателей и частоте вращения рабочих органов машин – орудий (п2), например
шпинделей станков, колес автомобиля и т.д. Чаще применяют
понижающие передачи, где п1> п2, реже встречаются повышающие передачи.
Понижающая передача называется редуктором, а повышающая – мультипликатором.
В курсе «ДМ» рассматриваются понижающие передачи
вращения.
1.1. Краткая классификация механических передач
вращения
Передачи с непосредственным соприкосновением
а) передачи зацеплением – зубчатые, червячные;
б) передачи трением – фрикционные.
10
11.
Передачи с промежуточным элементома) передачи зацеплением – цепные;
б) передачи трением – ременные (плоско и клиноременные).
Зубчато-ременные передачи можно отнести и к передачам
зацеплением, и к передачам трением.
При расчете передач используют следующие зависимости
между различными параметрами:
D n D Dn
– окружная скорость
V =
(м/с),
2 30 2
60
где D (м), n (мин-1);
– вращающий момент
Т = 9550 P (Н·м),
n
-1
где P (кВт), п (мин );
Т = F t D (Н·м),
2
где Ft (Н) – окружное усилие, D (м) – диаметр вала или шкива;
F V
P= t
(кВт),
– мощность
1000
где Ft (Н), V (м/c);
P = Tп (кВт),
-1
9550
где T (Н·м), п (мин );
– окружное усилие Ft = TD 2T (Н),
D
2
где T (Н·м), D (м);
Ft = 1000P (Н),
V
где P (кВт), V( м/c);
11
12.
п1 D2.
п2 D1
В теоретических дисциплинах пользуются понятием передаточного отношения i, а в курсе «Детали машин» используют
понятие передаточного числа U ≥ 1;
P
– коэффициент полезного действия η 2 ,
P1
где P1 – мощность на ведущем звене; Р2 – на ведомом.
Для ряда последовательных передач общее передаточное
число U = U1 ∙ U2 ∙ U3 ∙ …, а общий КПД η = η 1· η2 · η3 ·…
– передаточное число U =
1.2. О контактных напряжениях
Контактными называются напряжения, возникающие от
сжимающих сил на поверхностях соприкосновения двух деталей, когда площадки контакта очень малы. Контактные напряжения возникают у тел с криволинейными рабочими поверхностями (рис. 1.1 и 1.2).
Две сжатые плоскости работают не на контактные напряжения, а либо на напряжения сжатия (неподвижные), либо на
износ (подвижные).
На контактные напряжения работают и рассчитываются
как неподвижные, так и движущиеся детали, например, концевые цилиндрические и шаровые опоры у балок и ферм, зубчатые, червячные и фрикционные передачи, шариковые и роликовые подшипники, колеса и рельсы кранов железнодорожного
транспорта.
Впервые контактную задачу решил Г. Герц в 1881 г. Он
вывел формулу для определения контактных напряжений для
сжатых цилиндров:
qEпр
H = 0,418
(МПа)
пр
и для сжатых шаров: H
Fn E 2
0,388 3
(МПа),
2
p
12
13.
Fn– погонная нагрузка (нагрузка на единицу длины
b
H
контактной линии) ;
м
2 Е1 Е2
Eпр
– приведенный модуль упругости (МПа);
Е1 Е2
ρпр – приведенный радиус кривизны (м);
1
1
1
1
– приведенная кривизна:
=
.
2
пр
пр 1
где q
Рис. 1.1. Контактные напряжения при сжатии двух цилиндров
13
14.
Рис. 1.2. Деформация микрообъемов материалапри качении цилиндра по плоскости
Знак «+» относится к внешнему касанию, а знак «–» – к
внутреннему.
d1 и d2 – диаметры сжимаемых цилиндров.
b – длина цилиндров (длина контактной линии) (м);
Fn – сила сжатия цилиндров (Н);
Е1 – модуль упругости материала первого цилиндра (МПа);
Е2 – модуль упругости материала второго цилиндра (МПа).
Разрушение от повторных контактных напряжений (питтинг) носит характер усталостного выкрашивания, т.е. образование на поверхности отдельных выемок.
Схема этого процесса:
Рис. 1.3. Схема питтингообразования
14
15.
Усталостное выкрашивание наблюдается лишь при наличии смазки. Без смазки или с бедной смазкой имеет место изнострущихся поверхностей.
Если при работе детали напряжения меняются, например от
растягивающих до сжимающих, сотни и даже тысячи раз в секунду, то в таких условиях сталь может не выдержать – она «устает» – происходит усталостное разрушение. Подобное разрушение особенно опасно тем, что ему не предшествует заметная
пластическая деформация, которую можно было бы обнаружить
заблаговременно; кроме того, оно наступает при нагрузках значительно ниже предела прочности данной стали при растяжении,
сжатии или изгибе.
Во избежание контактного разрушения должно быть выдержано условие:
H ≤ [ ]Н (МПа).
Допускаемые контактные напряжения при статических нагрузках можно принимать [ ]Н = (2…3) т, а при переменных
нагрузках принимают:
[ ]Н= f (HB) или [ ]Н= f (HRC).
Числовые значения контактных напряжений намного превышают как значения других видов напряжений (растяжения,
изгиба), так и механических характеристик материала при одноосном напряженном состоянии: т и В. Отсутствие мгновенного разрушения при наличии столь высоких напряжений объясняется тем, что в зоне их действия материал находится в условиях всестороннего объемного сжатия.
15
16.
Глава 2. ЗУБЧАТЫЕ ПЕРЕДАЧИ2.1. Общие сведения
Зубчатые передачи – наиболее распространенный вид механических передач. Они обладают высокой нагрузочной способностью и, как следствие, малыми габаритами, высоким КПД –
0,97…0,98 в одной ступени, постоянством передаточного числа,
возможностью передавать большие мощности – до 50000 кВт.
К недостаткам зубчатых передач следует отнести шум при
высоких скоростях и повышенные требования к точности изготовления.
Зубчатые передачи бывают цилиндрические и конические с
прямым, косым, шевронным и криволинейным зубом (рис. 2.1).
Рис. 2.1. Виды зубчатых передач
16
17.
Профилировка зубьев производится по эвольвенте (предложено Эйлером в 1760 г.).Эвольвентой называется кривая, описываемая какой-либо
точкой, лежащей на прямой линии, перекатываемой по окружности без скольжения (рис. 2.2). Перекатываемая по окружности прямая называется производящей прямой, а окружность, по
которой перекатывается производящая прямая, – основной окружностью.
Рис. 2.2. Схема образования эвольвенты
Производящая прямая (общая нормаль NN) называется
линией зацепления, т.е. траекторией общей точки контакта сопряженных зубьев при ее движении.
Угол w между линией зацепления и прямой, перпендикулярной межосевой линии, называется углом зацепления (рис. 3.1).
В качестве материалов для зубчатых передач применяют
чаще всего углеродистые и легированные стали, реже – стальное литье, чугуны, пластмассы. Стали применяют после термообработки:
− объемной (нормализация, улучшение, отжиг);
− поверхностной (закалка ТВЧ, цементация, азотирование,
цианирование).
17
18.
2.2. Виды зубчатых передачРазличают следующие виды зубчатых передач:
– закрытого типа – редукторы. Они имеют специальный
корпус с крышкой, с индивидуальными валами, подшипниками,
полумуфтами. Изготовление точное, смазка обильная;
– открытого типа – защищенные лишь ограждением (кожухом). Изготовление и монтаж менее точный, смазка бедная
или отсутствует вовсе.
Расчет закрытых зубчатых передач производится на контактную прочность с учетом переменности нагрузки.
Условно все передачи в зависимости от твердости поверхностного слоя зубьев разделены на прирабатывающиеся (с твердостью НВ 350) и неприрабатывающихся (с твердостью НВ > 350).
Для обеспечения лучшей прирабатываемости зубчатых пар рекомендуется назначать твердость зубьев шестерни больше, чем
твердость зубьев колеса в соответствии со следующей эмпирической зависимостью:
НВ1min = НВ2min + (15) (20…30) (50),
где НВ1min – минимальная твердость материала шестерни;
НВ2min – минимальная твердость материала колеса.
Проверочный расчет производится по прочности зубьев на
изгиб. Этот расчет производится также с учетом переменности
нагрузки и концентрации напряжений у основания зуба.
Расчет передач открытого типа производится по прочности зубьев на изгиб с проверкой на контактные напряжения.
При тех и других расчетах учитывают:
– концентрацию нагрузки (не напряжений) по длине зуба
от упругих и монтажных перекосов валов и других деталей.
(рис. 2.3). Учитывается введением в расчет коэффициента Кβ;
− динамичность приложения нагрузки (удары в зубьях),
зависящую от неточности изготовления, окружной скорости,
соударяющихся масс, упругости системы и т.д. Учитывается
введением коэффициента Кv;
− неравномерность распределения нагрузки между зубьями, одновременно находящимися в зацеплении. Учитывается
введением коэффициента К ;
18
19.
Рис. 2.3. Схема образования зоны концентрации нагрузки− переменность нагрузки по времени (T = соnst бывает
редко).
В качестве примера можно привести график загрузки редукторов приводов к эскалаторам метрополитена (рис. 2.4).
Рис. 2.4. Циклограмма нагружения редуктора эскалатора
19
20.
Глава 3. ЦИЛИНДРИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ3.1. Расчет цилиндрических зубчатых передач
на контактные напряжения
Это основной вид проектного расчета. При расчете на контактные напряжения всем обозначениям соответствует индекс
Н (Н. Hertz).
Предпосылки к расчету:
1. Зубцы считаются эквивалентными сжатым цилиндрам с
радиусами, равными радиусам кривизны эвольвенты в полюсе
зацепления, для которого и подсчитываются контактные напряжения.
2. Усилие предполагается равномерно распределенным по
длине зуба.
3. Предполагается, что в зацеплении одновременно находится только одна пара прямых зубьев (однопарное зацепление).
Рис. 3.1. Схема к расчету зубьев на контактную прочность:
1 – эпюра контактных напряжений
20
21.
В основу расчета положена формула Герца для сжатых цилиндров:qEпр
H = 0,418
≤ [ ]Н ;
(3.1)
пр
Ft
Fn
Н
=
(3.2)
,
b сosα w b м
где b – ширина зубчатого колеса (длина контактной линии);
1000P1
d n
Ft1 =
(Н), V = 1 1 (м/с),
V
60
F d
2T
T1 t 1 (Н м), Ft1 1 (Н).
d1
2
1
1 1
Для внешнего зацепления:
= + .
(3.3)
пр 1 2
Из теории эвольвентного зацепления известно, что радиус
кривизны эвольвенты в полюсе зацепления определяется из
∆О1ВК и ∆О2ДК:
d
d
ρ1= 1 sin α w ;
ρ2= 2 sin α w .
2
2
2 1 1
2 d1 d 2
1
.
Тогда
=
пр sin α w d1 d 2 sin α w d1d 2
q=
d1 d 2 2aw
Кроме того d 2
d U
1
2 aw
2a w
Отсюда d1 =
, d2 = d1 ∙U =
U ;
U 1
U 1
2
2aw U 1 2
U 1 2
1
=
.
аw U sin α w
пр sin α w
4аw2 U
1
Подставляя полученное значение
и q в исходную форму пр
лу Герца (3.1) и принимая для стальных зубчаток Ест = 2 ∙ 105 МПа,
21
22.
sin 2α sin 40 0,64а также упрощая sinαwcosαw=
= 0,32 и вво
2
2
2
дя в расчет коэффициент нагрузки КН = КНβ ∙ KНV ∙ KН , получаем расчетную формулу для определения контактных напряжений в прямозубых цилиндрических передачах:
9600 T1 K H (U ' 1)3
H
H = (МПа).
(3.4)
wст
b2 U '
Это формула проверочного расчета. Чтобы получить форb
мулу проектного расчета, вводим коэффициент ψ bа = 2 и разaw
решаем ее относительно aw:
T K
(мм).
(3.5)
aw 450 U 1 3 2 1 Н
[ ]Н U ψbа
Для косозубой и шевронной передачи формула проектного
расчета имеет вид:
T K
(мм),
(3.6)
aw 410 U 1 3 2 1 Н
[ ]Н U ψ bа
а проверочного
3
8400 T1 K Н U ' 1
(3.7)
Н
[ ]Н (МПа),
'
аwст
b2 U
где Т1 (Н·м), b2 (мм), аw (мм).
Если расчетное напряжение H меньше допускаемого
[ ]H в пределах до 15% или H больше [ ]H в пределах до 5%,
то принятые параметры принимают за окончательные. Если же
действительное контактное напряжение превышает указанные
величины, то необходимо изменить либо выбранные материалы, либо геометрические параметры передачи ψ bа или аw и
произвести расчет заново.
Коэффициент ширины колеса относительно межосевого
b
расстояния ψ bа = 2 при твердости материала зубчаток НВ 350
aw
принимают:
22
23.
а) при симметричном расположении колес относительноопор ψ bа = 0,3…0,63;
б) при несимметричном ψ bа = 0,2…0,4;
в) при консольном ψ bа = 0,2…0,25.
При проектировании стандартных редукторов значение
ψ bа необходимо выбирать из стандартного ряда:
ψ bа = 0,1; 0,125; 0,16; 0,2; 0,25; 0,315; 0,4; 0,5; 0,63; 0,8; 1,0… (3.8)
Определение корректирующего коэффициента нагрузки
КН и коэффициента неравномерности распределения нагрузки
между зубьями у косозубых и шевронных передач КНα см. ниже.
Найденное значение аw необходимо округлить до стандартного значения из следующего ряда (ГОСТ 2185-66):
аw=40; 50; 63; 71; 80; 90; 100; 112; 125; 140; 160; 180; 200;
224; 250; 280; 315;…мм.
(3.9)
Найденное стандартное межосевое расстояние аw необходимо «разбить» между модулем т и суммой зубьев Z шестерни и колеса.
3.2. Определение модуля и числа зубьев шестерни и колеса
Прямозубые цилиндрические передачи
Рис. 3.2. Схема прямозубой цилиндрической передачи
23
24.
1. Материал зубчаток НВ ≤ 350По эмпирической формуле определяют т или тп:
т или тп = (0,01…0,02) аwст (мм)
(3.10)
и округляют до значения из стандартного ряда: т1 = 1; 1,125;
1,25; 1,375; 1,5; 1,75; 2,0; 2,25; 2,5; 2,75; 3; 3,5; 4; …(мм). (3.11)
Поскольку аw =
то Z
d1 d 2 mZ1 mZ 2 m Z1 Z 2 mZ
,
2
2
2
2
2a w
.
m
(3.12)
Должно быть Z 200.
Модуль подбирают таким образом, чтобы число зубьев было целым. Например, не может быть т = 3 мм при аw = 200 мм.
Примечание: длина окружности l = d или l = P Z, где
Р – шаг по делительной окружности, отсюда d = P Z,
P
P
d Z m Z , m – отношение шага по делительной окπ
π
ружности к называется модулем.
Z
Z
Поскольку Z Σ Z1 Z 2 , а 2 = U, то Z1 Σ округляют
Z1
U 1
до целого числа, а Z 2 Z Z1.
Должно быть Z1 17.
После этого корректируют передаточное число и частоту
вращения колес:
Z
n
U ' 2 , n2 1' (мин-1).
(3.13)
Z1
U
2. Материал зубчаток НВ > 350
В этом случае модуль определяют по эмпирической формуле:
т или тп = (0,016…0,035) аw (мм)
24
(3.14)
25.
и выбирают его стандартное значение из ряда (3.11), а весьдальнейший расчет ведут так, как и в первом случае.
Косозубые цилиндрические передачи
Рис. 3.3. Схема косозубой цилиндрической передачи
1. Материал зубчаток НВ ≤ 350
У косозубых (и шевронных) передач различают два шага и
соответствующие им модули:
– нормальный модуль тп – стандартный, по которому
P
осуществляют нарезку и контроль зубьев, mn n ;
– окружной модуль тt – нестандартный, по которому производят определение диаметральных размеров передач
P
m Z
( d mt Z n ); mt t .
cos β
Предварительно принимают = 12o, cos 12o = 0,9781 и находят суммарное число зубьев косозубой передачи1:
Z
2awст сosβ
.
mnст
(3.15)
Полученное значение Z округляют до целого числа. Затем находят действительное значение угла наклона зубьев:
β arccos
1
mnст
.
2аwст
Угол можно принимать в допустимых пределах 8o…15о.
25
(3.16)
26.
По формуле (3.16) однозначно находят угол , величинакоторого остается дробной, ее округлять нельзя. Точность вычислений 0,0001. Угол наклона должен быть в пределах
= 8о…15о. В целях унификации шестерни принято делать с
левым наклоном зубьев, а колеса – с правым2. Левым наклоном
называют такое направление зубьев, при котором любая его
точка движется против часовой стрелки при удалении вдоль зуба, если смотреть со стороны торца.
Число зубьев шестерни (округляют до целого числа):
Z кос
Z1
.
(3.17)
U 1
Число зубьев колеса:
Z 2 Z кос Z1 .
(3.18)
Число зубьев шестерни должно быть Z1 Z1min = 17 cos 3 β .
После этого корректируют передаточное число и частоту
вращения колес:
Z
n
U ' 2 ; n2 1' (мин 1 )
Z1
U
Шевронные передачи
Модуль передачи определяют в зависимости от межосевого расстояния
mn = (0,01 … … 0,02) awст (мм)
и выбирают его стандартное значение из ряда (3.11). Принимая
предварительно = 30о, cos 30o = 0,866, определяют суммарное
число зубьев шевронной передачи3:
2a
cos β
округляется до целого числа.
(3.19)
Z wст
mnст
Действительное значение угла наклона зубьев:
m Z
β arccos nст
(3.20)
не округлять.
2awст
2
3
Данная рекомендация не является обязательной.
Угол можно принимать в допустимых пределах 25o…40о.
26
27.
Число зубьев шестерни:Z
Z1
(3.21)
округляется до целого числа.
U 1
Число зубьев колеса:
Z2 = Z – Z1.
(3.22)
Число зубьев шестерни должно быть Z1 Z1min = 17 cos 3 β .
После этого корректируют передаточное число и частоту
вращения колес:
Z
n
U ' 2 ; n2 1' (мин 1 )
Z1
U
tn
в tg
tt
Проверка косозубой передачи по осевому шагу Рх
Для косозубой передачи (но не для шевронной) необходимо выполнить проверку по осевому шагу для того, чтобы убедиться, что проектируемая передача работает как косозубая, а
не как прямозубая.
tа
в
Рис. 3.4. Проверка косозубой передачи по осевому шагу Рх
Для этого необходимо следующее условие (рис. 3.4):
27
28.
Pnm
nст < b или Рt < b tgβ
(3.23)
sin β
sin β
У шевронной передачи вследствие больших значений углов β это условие удовлетворяется автоматически.
Преимущества косозубой передачи перед прямозубой:
− большая плавность и бесшумность работы;
− выше допускаемые окружные скорости (поэтому в двух
и более ступенчатом редукторе быстроходную ступень обычно
выполняют косозубой);
− лучшая прирабатываемость (так как зубцы входят в зацепление вершиной);
− бóльшая нагрузочная способность.
Основным недостатком косозубой передачи (но не шевронной) является наличие осевого давления на валы и подшипники. В настоящее время нарезание косого зуба не сложнее, чем
прямого.
Несколько сложнее (и дороже) нарезание шевронных
зубьев.
Px =
3.3. Корректирующие коэффициенты нагрузки
Выше уже отмечалось, что расчетный момент определяют
как Tрасч = Tном∙К (или расчетная мощность Pрасч = Pном∙К),
где К – корректирующий коэффициент нагрузки. При расчете
на контактную прочность он обозначается КН.
КН = КН КНV КН ,
(3.24)
где КНβ – коэффициент концентрации нагрузки по длине контактных линий;
КНV – коэффициент динамической нагрузки;
КН – коэффициент неравномерности распределения нагрузки между зубьями.
Коэффициент концентрации нагрузки КНβ учитывает неравномерность распределения нагрузки по длине зуба, которая
зависит от монтажных и упругих перекосов валов, опор, корпусов
28
29.
и самих зубчатых колес. Величина этих деформаций в свою очередь зависит от расположения передачи относительно опор.Передача
без нагрузки
Передача
под нагрузкой
Рис. 3.5. Схема для определения коэффициента концентрации нагрузки
На рисунке 3.5 изображено взаимное расположение колес
у передачи без нагрузки и под нагрузкой. Под действием сил в
зацеплении валы деформируются и происходит перераспределение нагрузки по длине зуба.
В общем виде коэффициент концентрации нагрузки определяется следующим образом:
q
КНβ= max >1.
q
Определение сил в зацеплении см. ниже.
Среднее значение погонной нагрузки q определить достаточно просто, однако определить qmах в каждом конкретном
случае затруднительно, поэтому при расчетах пользуются табличными данными.
Для прирабатывающихся передач, т.е. для передач с твердостью поверхностного слоя хотя бы одной из зубчаток
НВ < 350, можно принимать КНβ из табл. 3.1 в зависимости от
коэффициента ширины колеса относительно диаметра bd. Коэффициент bd рассчитывают по формуле:
ψbd 0,5ψbа (U 1) .
29
(3.25)
30.
Таблица 3.1Значения коэффициента КН при твердости рабочих
поверхностей шестерни и колеса НВ < 350
Расположение
передач относительно опор
Симметричное
Несимметричное
Консольное
Значения КН при bd
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,02
1,03
1,06
1,03
1,05
1,12
1,04
1,07
1,19
1,05
1,12
1,27
1,06
1,15
-
1,07
1,19
-
1,08
1,25
-
1,10
1,28
-
Чтобы уменьшить концентрацию нагрузки, рекомендуется:
а) рационально располагать передачу относительно опор –
лучше всего симметрично, хуже – несимметрично, еще хуже –
консольно;
б) увеличивать жесткость валов, корпусов, опор и т.д.
в) повышать точность изготовления и монтажа передачи.
Коэффициент динамической нагрузки КНV учитывает
динамичность приложения нагрузки (удары в зубцах), зависит
от неточности изготовления, окружной скорости и соударяющихся масс. Аналитический расчет представляет трудности, поэтому его можно принимать для прирабатывающихся передач в
зависимости от степени точности передачи и окружной скорости по табл. 3.2.
Таблица 3.2
Значения КНV
Степень
точности
изготовления
7
8
9
Прямозубая передача
при V, м/с
V < 5 м/с
V = 5–10 м/с
1,04–1,20
1,2–1,40
1,05–1,24
1,24–1,48
1,12–1,28
1,28–1,56
Косозубая и шевронная
передача при V, м/с
V < 5 м/с
V = 5–10 м/с
1,02–1,08
1,08–1,16
1,02–1,10
1,10–1,19
1,06–1,11
1,18–1,22
Интервалами окружных скоростей при определении значения коэффициента динамической нагрузки предварительно
задаются.
При этом большие значения КНV соответствуют большим
окружным скоростям.
30
31.
Для уменьшения динамичности приложения нагрузки следует повышать точность изготовления передач, использоватькосозубые и шевронные передачи.
Коэффициент неравномерности распределения нагрузки между зубьями КН . Значения коэффициента КН определяют в зависимости от степени точности передачи и окружной
скорости по табл. 3.3.
Таблица 3.3
Значения коэффициента КH
Степень точности
изготовления
7
8
9
при V<5 м/с
при V = 5–10 м/с
1,03
1,07
1,13
1,07
1,13
1,17
В проектном расчете окружная скорость еще неизвестна, поэтому интервалом скоростей и, следовательно, значением КH
предварительно необходимо задаться с последующим уточнением.
3.4. Допускаемые контактные напряжения
при расчете цилиндрических зубчатых передач
Определение допускаемых контактных напряжений основывается на кривых контактной усталости (кривых Велера).
Рис. 3.6. Кривая контактной усталости
31
32.
По кривой усталости (для криволинейной ее ветви) можнонаписать:
Нm ∙ NHE = Нlimm ∙ NHG = const.
N
Откуда Н = Нlim∙ т HG МПа.
N HE
При расчете на контактные напряжения т = 6 для стальных колес, а для чугунных колес т = 8.
NHG – базовое число циклов. При расчете на контактную
прочность NHG можно принимать по табл. 3.4 или более точно
определить по формуле:
NHG = 30 НВср2,4 циклов.
(3.26)
Таблица 3.4
Средняя
твердость
поверхности
зубьев
НВср
< 220
250
300
350
-
-
-
HRC
-
27
33
38
40
45
50
1,0
1,7
2,5
3,6
4,4
6,0
8,0
NHG 107 циклов
Если эквивалентное число циклов нагружения NHЕ > NHG,
то передача проектируется для длительной работы, т.е. в зоне
горизонтальной ветви кривой усталости. Тогда принимают:
N
т HG = 1, а Н = Нlim.
N HE
Если NHG >NHE, то передача проектируется для кратковременной работы и для нее H > Нlim.
Эквивалентное число циклов нагружения за весь срок
службы передачи определяется:
– для шестерни NHЕ1 = 60 ∙ п1 ∙ ТHE циклов;
(3.27)
– для колеса NHE2 = 60 ∙ п2 ∙ ТHE циклов.
(3.28)
Здесь ТHE (час) – эквивалентное число часов за весь срок
работы передачи.
Как правило, зубчатые передачи во время работы испытывают переменные нагрузки по времени, которые задаются суточным графиком нагрузки (рис. 3.7).
32
33.
ММ
М
Мпуск
Мкр
tпик
t
t
и т.д.
t
t (час)
Рис. 3.7. Циклограмма нагружения передачи
Время ТHE (час.) называется эквивалентным, так как приводится к одному режиму, обычно к максимальному моменту T,
пренебрегая режимом Tпуск ввиду его кратковременности
(tпик – сек.).
ТHE = tHE ∙ g ∙ L,
(3.29)
где g – число рабочих дней в году (260 при 5-дневной рабочей
неделе и 300 – при 6-дневной);
L – число рабочих лет.
В общем виде суточное эквивалентное время работы определяется по формуле:
т
п T 2
т
п T 2
tНE = t + t' t ... (час),
п T
п T
где n, п , п – частота вращения на каждом режиме работы.
В приводах от электродвигателей n п п … и тогда в
частном случае:
tHE = t +
т
T 2
t'
T
т
T 2
t
T
... (час).
(3.30)
При постоянной нагрузке (опять пренебрегая Tпуск):
tHE = t = число рабочих часов в сутки (час).
Длительное допускаемое контактное напряжение определяется так:
H lim = Hlim (МПа),
(3.31)
SH
33
34.
где H lim – предел контактной выносливости материала;SH – коэффициент безопасности, который принимают при
расчете на контактную прочность SH ≥ 1,1 для нормализованных и улучшенных зубьев и SH ≥ 1,2 для зубьев с поверхностным упрочнением (обычно SH = 1,1…1,75).
Предел контактной выносливости H lim для нормализованных и улучшенных зубьев с твердостью НВ < 350 определяют по формуле:
H lim = 2НВср + 70 (МПа),
(3.32)
а для объемно закаленных зубьев с твердостью НRС 45…55
H lim = 18НRC + 150 (МПа).
(3.33)
Редко на практике применяют зубчатые передачи, у которых
шестерня и колесо выполнены из одного и того же материала и с
одинаковой термообработкой, как, например, зубчатки коробок
передач. В этом случае более опасным на контактные напряжения
будет зуб шестерни (в U раз чаще вступающий в зацепление, чем
зуб колеса), следовательно, здесь расчетное H H 1.
Гораздо чаще на практике для компенсации бóльшего числа циклов нагружения шестерня выполняется из лучшего материала или с лучшей термообработкой. Рекомендуемые соотношения:
НВ1min= НВ2min + (15)20… 30(50).
(3.34)
В этом случае ввиду более слабого материала колеса расчет на контактные напряжения ведут по H H 2 .
Исключением являются косозубые и шевронные передачи,
для которых за расчетное допускаемое контактное напряжение
принимают:
H = 0,45( H 1 + H 2 ) при этом должно быть
H 1,25 min (МПа).
(3.35)
Меньшее из этих двух значений и принимают за расчетное.
Технологические преимущества сталей с НВ 350 обусловили их широкое применение в условиях индивидуального и
мелкосерийного производства, в мало- и средненагруженных
передачах, а также в передачах с большими колесами, термическая обработка которых затруднена.
34
35.
3.5. Расчет зубчатых передач по прочности зубьев на изгибПри расчете на изгиб всем обозначениям соответствует
индекс F (от англ. foot – ножка).
Этот расчет, как правило, носит проверочный характер.
Предпосылки расчета (рис. 3.8):
− зуб рассматривается как балка, заделанная одним концом с опасным сечением, проходящим через радиусы закруглений у основания зуба;
− усилие от сопряженного зуба прикладывается к вершине зуба под углом зацепления αw (худший случай);
− усилие равномерно распределяется по длине зуба;
− в зацеплении одновременно находится лишь одна пара
зубьев (прямых).
Рис. 3.8. К расчету зубьев на изгиб
35
36.
Переносим силу Fn по линии ее действия в точку С и разлагаем ее на две составляющие силы:– окружную силу Ft = Fn ∙ cos αw;
– радиальную силуFr = Fn ∙ sin w.
Для любой передачи исходной для определения всех сил
является окружная сила Ft, которая определяется:
2T
Ft = 1000P (Н) или Ft =
(Н),
V
D
где P (кВт), V (м/с), T (Н·м), D = m ∙z (м).
Ft
Сила Fr = Ft ∙ tgαw, а сила Fn =
.
сosα w
Сила Ft изгибает зуб у основания моментом Мизг = Ft∙l с
соответствующим напряжением изгиба:
F l 6F l
изг= М изг t 2 t 2 (МПа).
Wизг bS
bS
6
Сила Fr сжимает зуб с напряжением у основания:
сж =
Fr Fr
(МПа).
A bS
Максимальное напряжение сжатия будет в точке В:
max = изг + сж.
Однако практика показала, что усталостное разрушение
зубьев (появление и развитие усталостных трещин) всегда имеет место в зоне растяжения, т.е. в точке А (стальные и чугунные
детали лучше работают на сжатие, чем на растяжение), поэтому
расчет на изгиб ведут по номинальному напряжению в точке А:
F = изг – сж ≤ [ ]F.
Преобразуем эту формулу:
F=
6 Ft l Fr 6Ft l Fr S 6Fnl cos w Fn sin w S m
m .
bS 2 bS bS 2 bS 2
bS 2
36
37.
Ft, получаем:
cos w
Ft
6l m cos w S m sin w
F=
.
m b cos w
S2
1 6l m cos w S m sin w
Обозначив
= YFS (3.37)
cos w
S2
и учитывая, что Ftрасч = Ft∙К, получаем окончательную формулу
для расчета напряжений изгиба у зубьев колеса (предположительно как наиболее слабого):
Подставляя Fn =
F2 =
Ft 2 K F YFS 2
≤ [ ]F2 (МПа).
mcт b2
(3.38)
Значения ширины зубчатого колеса b2 и модуля тст подставляют в расчетную формулу в миллиметрах.
Напряжения изгиба у зубьев шестерни:
F1 = F2
YFS1
≤ [ ]F1 (МПа).
YFS 2
(3.39)
Расчетная формула для косозубой и шевронной передач
имеет вид:
F K Y Y
(3.40)
F2 = t 2 F FS 2 Fβ ≤ [ ] F2 (МПа),
mпст b2
2T
где Ft2 = 2 – окружное усилие на колесе, Н;
d2
d2 – делительный диаметр колеса, м;
b2 – ширина зубчатого колеса, мм;
YFS2 – коэффициент формы зуба, значение которого выбираются для некорригированных передач в зависимости от числа
зубьев Z для прямозубых передач и ZV – для косозубых и шевронных по табл. 3.5.
ZV =
Z
cos 3 β
37
(3.41)
38.
Таблица 3.5Значения коэффициента YFS в зависимости от Z и Zv
Z или Zv
YFS
17
4,28
18
4,23
19
20
4,15 4,09
Z или Zv
27
28
29
YFS
3,86
3,84
3,82
21
4,05
22
4,01
23
3,97
24
3,93
30
40
50
60
80
3,8
3,7
3,66
3,62
3,61
25
3,9
26
3,88
100 и
более
3,6
KF – коэффициент нагрузки при расчете на изгиб:
KF = KF KFV KF ;
(3.42)
KF – коэффициент концентрации нагрузки, который выбирают по табл. 3.6 в зависимости от коэффициента ширины
шестерни относительно диаметра bd при НВ < 350 ( bd рассчитывают по формуле 3.24).
Таблица 3.6
Значения коэффициента KF
bd
KF
0,2
1,0
0,4
1,02
0,6
1,05
0,8
1,07
1,0
1,10
1,2
1,12
1,4
1,17
1,6
1,2
KFV – коэффициент динамической нагрузки выбирают из
табл. 3.7 в зависимости от степени точности и окружной скорости V , м/с.
Таблица 3.7
Значения коэффициента KFV для передач с НВ < 350
Степень
точности
7
8
9
1
2
1,08
1,03
1,10
1,04
1,11
1,04
1,16
1,06
1,20
1,08
1,22
1,08
Окружная скорость V, м/с
3
5
1,24
1,09
1,30
1,12
1,33
1,12
1,40
1,16
1,48
1,19
1,56
1,22
8
10
1,64
1,25
1,77
1,30
1,90
1,36
1,80
1,32
1,96
1,38
1,45
В числителе приведены значения для прямозубых колес, в знаменателе –
для косозубых.
38
39.
KF – коэффициент неравномерности распределения нагрузки между парами зубьев, одновременно находящихся в зацеплении. Его выбирают в зависимости от окружной скорости V (м/с) истепени точности изготовления передачи по табл. 3.8.
Таблица 3.8
Значения коэффициента KF
Степень точности
изготовления
передачи
7
8
9
Окружная скорость V, м/с
V < 5 м/с
V = 5–10 м/с
V = 10–15 м/с
1,07
1,22
1,35
1,20
1,30
-
1,25
1,40
-
YF – коэффициент повышения прочности косозубых и
шевронных передач по напряжениям изгиба:
Yβ
YF =
.
(3.43)
Y – коэффициент повышения прочности косозубых и
шевронных передач вследствие наклона контактной линии к
основанию зуба:
β
Y = 1 –
(3.44)
.
140
– коэффициент торцового перекрытия:
1 1
= 1,88 3,2 cos β .
Z Z
1 2
(3.45)
Расчет на изгиб производят для той зубчатки, у которой
отношение F меньше.
YFS
39
40.
3.6. Допускаемые напряжения изгибадля цилиндрических зубчатых передач
Как и допускаемые контактные напряжения, напряжения
изгиба определяются в зависимости от режима нагружения.
Вначале определяют эквивалентное время работы передачи в течение суток:
6
T
tFE = t + t час,
(3.46)
T
где t и t выбирают из циклограммы работы в задании.
Затем определяют эквивалентное время работы передачи
за весь срок службы TFE:
TFE = tFE д L = tFE 260 5 (час).
(3.47)
Значения д и L см. выше.
Эквивалентное число циклов нагружения зубьев в течение
всего срока службы передачи при расчете на изгиб определяют:
NFE = 60 n TFE (циклов).
(3.48)
Полученное значение эквивалентного числа циклов нагружения NFE сравнивают с базовым числом циклов нагружения NFG, которое при расчете на изгиб можно принимать NFG = 4 106 циклов.
Допускаемые напряжения изгиба [σ]F определяют по формуле:
N
[ ]F = F lim 6 FG Y A (МПа),
(3.49)
SF
N
FE
где F lim – предел изгибной выносливости при нереверсивной
работе и твердости поверхности зубьев НВ < 350, который определяют по формуле:
F lim = 1,8НВср (МПа);
(3.50)
SF = 1,55–1,75 – коэффициент безопасности для нормализованных и улучшенных зубьев;
40
41.
YА – коэффициент режима работы; для нереверсивной передачи YA = 1, для реверсивной YA = 0,7…0,8.N
Если число циклов нагружения NFE > NFG, то 6 FG приN FE
нимают равным 1 и [ ]F =
F lim
(МПа).
SF
(3.51)
3.7. Расчет цилиндрических зубчатых передач
на кратковременную перегрузку (т.е. на отсутствие
пластических деформаций или хрупкого разрушения)
Кратковременные перегрузки возникают, например, во
время пуска электродвигателя. Поверхностные слои зубьев хорошо сопротивляются перегрузкам, поэтому допускаемые напряжения в этом случае значительно выше.
По контактным напряжениям
H max H
Tпуск
Т
Н max (МПа),
(3.52)
где H max – максимальное контактное напряжение, возникающее во время пуска;
H – расчетное контактное напряжение, определяемое по
формулам (3.4) и (3.7);
Tпуск – максимальный момент, возникающий во время пуска;
Т – номинальный вращающий момент;
T
отношение пуск дано в задании (см. циклограмму нагрузки);
T
H max – максимальное допускаемое контактное напряжение при пусковой перегрузке, определяемое для нормализованных и улучшенных зубьев с НВ < 350 по формуле:
H max 2,8 т (МПа).
41
(3.53)
42.
По напряжениям изгибаF max F
Tпуск
T
F max ,
(3.54)
где F max – максимальное напряжение изгиба, возникающее
при пусковой перегрузке;
F – расчетное напряжение изгиба, определяемое по формулам (3.38) и (3.40);
Tпуск – максимальный момент, возникающий во время
пуска;
Т – номинальный вращающий момент;
T
отношение пуск дано в задании (см. циклограмму нагрузки);
T
F max – максимальное допускаемое напряжение изгиба
при пусковой перегрузке, определяемое для нормализованных и
улучшенных зубьев с НВ 350 по формуле:
F max 2,74 HBср (МПа).
(3.55)
3.8. Особенности расчета открытых цилиндрических
зубчатых передач
Открытые цилиндрические передачи выполняются только
с прямыми зубьями и применяются при окружных скоростях
колес менее 2 м/с. В этом случае назначают 9 степень точности
изготовления зубчатых колес, а расчет ведут по тем же формулам, что и при закрытых передачах, только в этом случае при
проектном расчете значение модуля увеличивается в 1,5…2
раза и определяется по формуле:
т = (0,02…0,04)аw (мм).
(3.56)
Вследствие абразивного износа такие передачи являются
прирабатывающимися при любой твердости поверхностного
слоя зубьев.
42
43.
Допускаемые контактные напряжения H и допускаемыенапряжения изгиба F принимают равными соответствующим
допускаемым напряжениям при длительной работе, т.е. считается, что
NНЕ> NНG и NFE > NFG;
H H lim и F F lim .
3.9. Степени точности цилиндрических зубчатых колес
Цилиндрические зубчатые колеса по точности изготовления разделены стандартом на 12 степеней, обозначаемых в порядке убывания точности от 1 до 12. Наибольшее распространение имеют 6, 7, 8 и 9 степени точности.
Степень точности изготовления зубчатых передач рекомендуется выбирать в зависимости от окружной скорости V (м/с) по
табл. 3.9.
Таблица 3.9
Рекомендуемые значения степени точности изготовления
передач в зависимости от окружной скорости [4]
Степень точности
6 (высокоточные)
7 (точные)
8 (средней
точности)
9 (пониженной
точности)
Окружная скорость V, м/с (не более)
Прямозубые
Косозубые
ЦилиндриЦилиндриКонические
Конические
ческие
ческие
20
12
30
20
12
8
20
10
6
4
10
7
2
1,5
4
3
Для каждой степени точности установлены три нормы.
1. Норма кинематической точности колес, регламентирующая погрешность углов поворота сцепляющихся колес за
один оборот.
2. Норма плавности работы, регламентирующая за один
оборот колеса колебания скорости, вызывающие шум и динамические нагрузки.
43
44.
3. Норма контакта зубьев, регламентирующая длину контактных линий, равномерность распределения нагрузки по ними определяющая работоспособность передачи.
Кроме того, стандартом предусмотрены шесть видов сопряжения колес, которые учитывают только величину бокового
зазора и не связаны со степенью точности передачи. Боковой
зазор необходим для предотвращения заклинивания зубьев передачи при нагреве, размещении смазки и для обеспечения свободного вращения колес. Он задается следующими видами сопряжений:
Н – нулевой зазор;
Е – малый;
С и Д – уменьшенный;
В – нормальный;
А – увеличенный.
Чаще всего применяют сопряжения вида В.
3.10. Силы в зацеплении и воздействия на валы
в цилиндрических зубчатых передачах
Цилиндрическая прямозубая передача (рис. 3.9)
Рис. 3.9. Силы в прямозубой цилиндрической передаче
Разлагаем силу Fn нормального давления на зуб (от сопряженного зуба) на составляющие Ft и Fr. Исходной для определения сил в любой передаче является окружная сила Ft:
44
45.
Ft = 2T 1000P (Н),V
d
(3.57)
dn
(м/c) , а d = m ∙ Z (м).
60
Тогда радиальная сила Fr = Ft ∙ tg αw (Н),
(3.58)
где αw – угол зацепления (20°), а сила
Ft
2
2
Fn =
Ft Fr .
(3.59)
сosα w
Переносим силы Ft и Fr из полюса зацепления (точка К) в
центр вала с добавлением пары Ft –Ft.
Вал нагружен:
− изгибающими силами Ft и Fr (либо их равнодействующей Fn);
d
− моментом от пары Ft – Ft: T = Ft ∙ .
2
Цилиндрическая косозубая передача (рис. 3.10)
где V =
d
W
Q
Рис. 3.10. Силы в косозубой цилиндрической передаче
45
46.
Разлагаем силу Fn нормального давления на зуб от сопряженного зуба на составляющие FR и Fr, а силу FR – на Ft и Fa .Получаем три взаимно перпендикулярных силы Ft, Fa и Fr.
Окружная сила Ft = 1000P (Н),
V
dn
где V =
(м/c).
60
Осевая сила Fa = Ft ∙tg β (Н),
где – β угол наклона зуба.
(3.60)
Радиальная сила Fr = FR ∙ tgαw=
Ft
∙ tg αw (Н),
сosβ
(3.61)
где αw – угол зацепления.
Cила Fn =
Ft
FR
2
2
=
Ft Fa 2 Fr .
сosα w cosα wсosβ
Переносим силы Ft, Fa и Fr из полюса зацепления (точка К)
в центр вала О с добавлением пар Ft –Ft и Fa –Fa.
Вал нагружен:
− изгибающими силами Ft и Fr и изгибающим моментом
от пары Fa – Fa;
− сжимающей (или растягивающей) силой Fa (в зависимости от места закрепления вала в подшипнике);
− моментом от пары Ft – Ft
T = Ft ∙
d
.
2
Шевронная передача (рис. 3.11)
F
У шевронной передачи силы a не передаются на вал, т.е.
2
вал испытывает изгиб силами Ft и Fr и скручивание парой
Ft –Ft.
46
47.
Рис. 3.11. Силы в шевронной передаче3.11. Смазывание зубчатых передач
Смазку зацепления при окружных скоростях до 12,5 м/с
применяют чаще всего картерную. В корпус редуктора или коробки передач заливают масло, образующее масляную ванну.
Объем смазки рекомендуется принимать не менее 0,25…0,8 л
на 1 кВт передаваемой мощности. Цилиндрические зубчатые
колеса рекомендуется погружать в масло на глубину
hм = (4т…0,25d2т), но не менее 10 мм. Однако часто объем масляной ванны принимается исходя из опыта эксплуатации конкретных редукторов в конкретных условиях. В этом случае он
может значительно отличаться от приведенных значений. Наибольшая допустимая глубина погружения зависит от скорости
колеса. Чем медленнее вращается колесо, тем на бóльшую глубину оно может быть погружено. Тихоходные колеса (второй и
третьей ступени) допустимо погружать на величину до 1/3 радиуса колеса.
Ассортимент масел, предназначенных для смазывания
промышленного оборудования, в том числе и редукторов, выделен по ГОСТ 17479-85 в отдельную группу с общим условным наименованием «Индустриальные масла».
Обозначение индустриальных масел состоит из группы знаков, разделенных между собой дефисом (например, И-Г-А-68).
Первая буква обозначает принадлежность к индустриальным маслам (И).
47
48.
Вторая буква – принадлежность к группе по назначению:Л – легконагруженные;
Г – гидравлические системы;
П – направляющие скольжения;
T – тяжелонагруженные узлы.
Третья буква указывает на уровень эксплуатационных
свойств:
А – масла без присадок;
В – масла с антиокислительными и антикоррозионными
присадками;
С – масла типа В с противоизносными присадками;
Д – масла типа С с противозадирными присадками;
Е – масла типа Д с противоскачковыми присадками).
Цифры в конце марки показывают класс кинематической
вязкости при 40°С.
Как известно, важнейшим свойством масел, определяющим их смазывающую способность, является вязкость.
Вязкость – это свойство сопротивляться сдвигу одного слоя
жидкости по отношению к другому. Для характеристики вязкости
пользуются понятием кинематической вязкости , мм2 /с (1 мм2 /с
называется сантистоксом). Вязкость масла обычно приводят в
справочниках при температурах, близких к рабочим, т.е. 40°,
50°, 100 °С.
Вязкость масла выбирается в зависимости от нагрузок
( Н, МПа), окружной скорости (V, м/с) и рабочей температуры
(°С); в цилиндрических и конических редукторах она обычно
составляет 40–50 °С (табл. 3.10, 3.11).
Таблица 3.10
Рекомендуемые значения кинематической вязкости масла
для смазывания зубчатых передач при температуре 40°С
Контактные
напряжения
н, МПа
До 600
600-1000
Кинематическая вязкость 40, мм2/с, при окружной
скорости колеса V, м/с
До 2
V = 2-5
Более 5
34
28
22
60
50
40
48
49.
Выбор сорта масла начинается с определения необходимой кинематической вязкости масла по табл. 3.10. Чем вышеконтактные напряжения, тем бóльшей вязкостью должно обладать масло; с увеличением окружной скорости вязкость масла
должна быть меньше. Затем выбирают соответствующее масло
по табл. 3.11.
Таблица 3.11
И-Г-А-68
Марка И-Л-А-22 И-Г-А-32 И-Г-А-46
И-Г-С-32 И-Г-С-46 И-Г-С-68 И-Т-Д-32 И-Т-Д-32
(И-40А,
масла (И-12А) (И-20А) (И-30А)
(ИГП-18) (ИГП-30) (ИГП-38) (ИСП-25) (ИРП-40)
И-50А)
Кинематическая
вязкость
19-25
29-35
41-51
61-75
24-30
39-50
55-65
28,8-35,2 61,2-74,8
Примечание. В скобках указано старое обозначение марок масла.
Срок эксплуатационной годности масла при нормальной
работе, т.е. при отсутствии попадания в масло пыли, влаги,
абразивных частиц, обычно составляет 10–15 тыс. часов работы, после чего масло теряет свои смазывающие свойства в
результате окисления.
При попадании пыли и влаги в масло процесс старения
значительно ускоряется. В этом случае смазку рекомендуется
заменять через каждые 2500–5000 часов работы.
Контроль уровня масла осуществляется либо при помощи щупа, либо при помощи окна, либо маслоуказателем с
трубкой из оргстекла.
В качестве уплотнительных устройств применяют манжетные уплотнения.
49
50.
Глава 4. КОНИЧЕСКИЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ4.1. Общие сведения
Конические зубчатые колеса применяются в передачах, у
которых оси валов пересекаются под углом. Наиболее распространена передача с углом 90 (рис. 4.1).
Передачи с межосевым углом 90 применяются редко
из-за сложности форм и технологии изготовления корпусных деталей. Прямозубые конические колеса применятся при окружных скоростях до 2…3 м/с. При более высоких скоростях применяют колеса с круговыми зубьями как обеспечивающие более
плавное зацепление, бóльшую несущую способность и более
технологичные. Конические зубчатые передачи выполняются
без смещения исходного контура или равносмещенными.
В коническом зацеплении действуют осевые силы, которые усложняют конструкцию опор. Схема конической передачи
представлена на рис. 4.1.
Рис. 4.1. Схема конической передачи
50
51.
На рисунке 4.1 1 и 2 – углы делительных конусов шестерни и колеса соответственно.d
Z
1 + 2 = 90о, 2 = 90о – 1, U e2 2 ;
d e1 Z1
d
Z
Z1 d e1 1
, tg 2 = e 2 2 .
(4.1)
Z 2 d e2 u
d e1 Z1
Размеры, относящиеся к внешнему торцовому сечению,
сопровождаются индексом «е», а размеры в среднем сечении –
индексом «m».
Re – внешнее конусное расстояние;
Rm – среднее конусное расстояние;
Rm = Re – 0,5b; b – ширина зубчатого венца.
de1 и de2 – внешние делительные диаметры шестерни и
колеса соответственно;
dae1 и dае2 – внешние диаметры вершин шестерни и колеса
соответственно.
В конических зубчатых передачах различают два модуля:
− внешний окружной модуль mte на диаметре dae1 и dae2,
по которому производится нарезка и контроль зубьев;
− окружной модуль в среднем сечении mtm , по которому определяется прочность зуба на контактные напряжения и
на изгиб. Эти модули связаны между собой следующей зависимостью:
b
mte Re
mte
Re
2 .
, откуда mtm
(4.2)
Re
mtm R b
e
2
tg 1 =
Поскольку наибольшее распространение среди конических передач получили передачи с круговыми зубьями, то в
дальнейшем будем рассматривать расчет этих передач.
Для них при n = 35o (см. ниже) и Кbe = 0,285:
− окружной модуль в среднем сечении mtm = mte 0,857;
− средний нормальный модуль mn = mtm cos n= 0,702 mte.
51
52.
Круговые зубья нарезают немодульным инструментом,поэтому допускается применять передачи с нестандартными
модулями, однако величины mnm для круговых зубьев и mte для
прямых зубьев рекомендуется согласовывать с ГОСТ;
n
Z
sin 2
− передаточное число U 1 2
ctg 1 tg 2 ; (4.3)
n2 Z1 sin 1
− внешний делительный диаметр шестерни и колеса соответственно
de1 = mte Z1; de2 = mte Z2;
(4.4)
– внешний диаметр вершин зубьев шестерни и колеса
d a e 1 = de1 + 1,64(1 + n1)mte cos 1;
d a e 2 = de2 + 1,64(1 + n2)mte cos 2,
(4.5)
где n1 и n2 – коэффициенты смещения инструмента для
шестерни и колеса, которые выбираются из табл. 4.1 в зависимости от Z1 и передаточного числа U.
Таблица 4.1
Коэффициент смещения инструмента n1
z1
12
13
14
15
16
18
20
25
30
40
2,5
0,37
0,35
0,33
0,31
0,30
0,27
0,26
0,21
0,18
0,14
Передаточное число U
3,15
4,0
0,39
0,41
0,37
0,39
0,35
0,37
0,33
0,35
0.32
0,34
0,30
0,32
0,28
0,29
0,24
0,25
0,21
0,22
0,16
0,17
5,0
0,42
0,40
0,38
0,36
0,35
0,32
0,29
0,25
0,22
0,17
Коэффициент смещения инструмента для колеса n2 = – n1.
β n – расчетный угол наклона кругового зуба на окружности
среднего диаметра колеса; он определяется как угол между касательной к окружности и образующей конуса в данной точке (рис. 4.2).
52
53.
Радиус r выбирается в зависимости от ширины зубчатоговенца «b», конусного расстояния Re, размера резцовых головок [5].
Рис. 4.2. Схема для определения угла n
4.2. Расчет конических зубчатых передач
с круговыми зубьями и с n = 35° на контактные напряжения
Чаще всего такие передачи применяются при U 5 и с коэффициентом относительной ширины зубчатого венца Кbe= b = 0,285.
Re
Для таких передач предварительное значение внешнего
делительного диаметра шестерни определяют по формуле:
d e 1 16503
K H T1
2
H
u H
(мм)
(4.6)
Полученное значение d'e1 округляют до ближайшего целого числа.
P
Расчетный момент на валу шестерни T1 = 9550 1 (Н·м).
n1
53
54.
Коэффициенты, учитывающие распределение нагрузкимежду зубьями для конической передачи с круговыми зубьями:
K Н 1 и K F 1.
Здесь коэффициент нагрузки КН = КН КНV.
Коэффициент концентрации нагрузки КН = 1...1,23 при
твердости одного или обоих зубчатых колес НВ 350.
Для предварительного расчета при НВ 350 можно
принимать К Н = 1,1.
При твердости обоих колес НВ > 350 К Н = 1,25...1,45.
Коэффициент динамической нагрузки КНV можно принимать в зависимости от степени точности изготовления для
колес с НВ 350 при V 5 м/c:
при 7-ой степени точности КНV = 1,02 – 1,08;
при 8-ой степени точности КНV = 1,02 – 1,10.
Для интервала скоростей V = 5–10 м/с и НВ 350:
при 7-ой степени точности КНV = 1,08 – 1,16;
при 8-ой степени точности КНV = 1,10 – 1,19.
Коэффициенты, учитывающие термообработку конических зубчатых колес при расчете на контактную прочность н и
при расчете прочности зуба на изгиб F, рассчитывают по эмпирическим зависимостям из табл. 4.2.
Таблица 4.2
Термообработка зубьев
Улучшение шестерни
и колеса
НВ1 и НВ2 350 НВ
ТВЧ, цементация
шестерни,
улучшение колеса
Н1 45 HRC;
Н2 350 НВ
н
1,22 + 0,21 U
1,13 + 0,13 U
F
0,94 + 0,08 U
0,85 + 0,04 U
ТВЧ, цементация
шестерни; ТВЧ,
цементация колеса
Н1 и Н2 45 HRC
0 ,8 1+0, 15 U
0,65 + 0,11 U
Определение допускаемых контактных напряжений см.
ниже.
Предварительное значение числа зубьев шестерни Z1 определяют по графику (рис. 4.3).
54
55.
Рис. 4.3. График для определения предварительного числа зубьев ZОкончательное значение числа зубьев шестерни Z1 находят по следующим зависимостям:
Z1 =1,6 Z'1 при Н1 и Н2 < 350 НВ
Z1 =1,3 Z'1 при Н1 > 45 HRC и Н2 350 НВ
(4.7)
Z1 = Z'1 при Н1 и Н2 > 45 HRC
Полученное значение Z1 округляют до целого числа и определяют число зубьев колеса: Z2 = Z1 U. Фактическое передаZ
точное число U 2 . Затем определяют углы делительных коZ1
нусов:
− угол делительного конуса колеса 2 = arctgU';
(4.8)
o
− угол делительного конуса шестерни 1 = 90 – 2. (4.9)
Точность вычислений 1 и 2 – 0,001.
Внешний окружной модуль
d
mte = e1 (мм), точность вычислений 0,0001.
(4.10)
z1
Внешнее конусное расстояние
m
Re = te Z12 Z 22 (мм), точность вычислений 0,001. (4.11)
2
Rm = Re – 0,5b = Re – 0,5 0,285 Re = 0,857 Rе .
(4.12)
55
56.
Ширина венцов зубчатых колесb1 = b2 = b = 0,285Re (мм)
(4.13)
округляется до целого числа.
Затем определяют окончательное значение геометрических параметров зубчатых колес.
Внешний делительный диаметр шестерни и колеса:
de1 = mte Z1 (мм); de2 = mte Z2 (мм);
d R
d m1 e1 m 0,857d e1 ; mtm = 0,857 mte.
Re
(4.14)
(4.15)
4.3. Проверочный расчет конических передач с круговыми
зубьями на контактные напряжения
После выполнения проектного расчета передачи необходимо произвести проверочный расчет по формуле:
Н 67000
К H T1
Н (МПа).
d e31 H U
(4.16)
Расчетное контактное напряжение H должно быть в интервале Н = (0,9 … 1,03) σ Н .
σ Н σ Н 100%
σ Н
(4.17)
4.4. Определение допускаемых контактных напряжений
Расчет величины допускаемых контактных напряжений
производится точно так же, как для косозубых или шевронных
передач с учетом режима нагружения. После определения σ Н 1
56
57.
и σ Н 2 находят расчетное допускаемое напряжение как меньшее из полученных значений:σ Н
= 0,45 ( σ Н 1 σ Н 2 ) или σ Н = 1,15 σ Н 2 .
(4.18)
4.5. Расчет конических зубчатых передач с круговыми
зубьями на изгиб
Напряжения изгиба в опасном сечении зуба колеса определяют по формуле:
2720К F T1 YFS 2
σF2
σ F 2 (МПа).
(4.19)
d e1 b1mte F
Коэффициент, учитывающий термообработку зубьев при
расчете на изгиб F, определяют по табл. 4.2.
Коэффициент нагрузки КF для конических передач с круговым зубом
КF = КF КFV,
где КF – коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба.
Можно принимать для передач с НВ 350 КF = 1,1, а коэффициент КFV выбирают так же, как и КНV (п. 4.2).
YFS2 – коэффициент прочности зубьев при расчете на изгиб
по номинальным напряжениям определяют по табл. 4.3 в зависимости от коэффициента смещения инструмента 2 = – 1 и эквивалентного числа зубьев ZV2:
ZV 1
Z1
Z1
Z2
Z2
. (4.20)
; ZV 2
3
cos β n cos δ1 0,55 cos 1
cos β n cos δ 2 0,55 cos 2
3
57
58.
Таблица 4.3Z
16
20
25
32
40
50
60
80
100
180
Коэффициент смещения инструмента
-0,5
-0,25
0
+0,25
Коэффициент YFS
–
–
4,28
3,78
–
–
4,07
3,64
–
4,30
3.90
3,62
4,50
4,05
3,78
3,59
4,14
3,88
3,70
3,57
3,96
3,78
3,66
3,54
3,82
3,71
3,62
3,54
3,78
3,66
3,60
3,55
3,68
3,62
3,60
3,56
3,64
3,62
3,60
3,58
+0,5
3,4
3,39
3,40
3,40
3,42
3,44
3,47
3,50
3,52
3,56
Напряжения изгиба для зуба шестерния:
YFS 1
σ F 2 σ F 1 (МПа),
(4.21)
YFS 2
где YFS1 – коэффициент прочности зуба для шестерни определяется
так же, как и для колеса по таблице 4.3 в зависимости от Zv1 и 1.
σ F1
4.6. Допускаемые напряжения изгиба для конических
зубчатых передач
Расчет величины допускаемых напряжений на изгиб производится точно так же, как и для цилиндрических передач с
учетом режима нагружения (см. выше).
4.7. Расчет конических зубчатых передач
на кратковременную перегрузку
Этот расчет производится так же, как и для цилиндрических передач (см. выше).
58
59.
4.8. Силы в зацеплении конических передачс круговыми зубьями
В передаче с круговым зубом во избежание заклинивания
зубьев в процессе зацепления необходимо осевую силу Fa1 на
ведущей шестерне направить к основанию конуса. Для этого
направление вращения ведущей шестерни (если смотреть со
стороны вершины делительного конуса) и направление наклона
зубьев должны совпадать.
Рис. 4.4. Схема сил в конической передаче
Окружную силу рассчитывают по формуле:
2 T1 103
Ft Ft1 Ft 2
,
(4.22)
d m1
где T1 (Н·м), a dm1 (мм) – средний делительный диаметр, определяемый по формуле: dm1=0,857 de.
Радиальная сила на шестерне:
Fr1 = Ft (0,44cos 1 – 0, 7sin 1) (Н).
(4.23)
Осевая сила на шестерне:
Fa1 =Ft (0,44 sin 1 + 0,7 cos 1) (Н).
(4.24)
59
60.
Силы на колесе равны соответственноFr2 = – Fa1 и Fa2 = – Fr1.
(4.25)
Приведенные зависимости справедливы при = w = 20o,
n = 35o и при совпадении направления наклона зубьев и направления вращения шестерни.
Глава 5. ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
5.1. Общие сведения и кинематика
Червячные передачи выпускаются и применяются реже зубчатых. Если все передачи зацеплением принять за 100%, то все
виды зубчатых передач составят примерно 85%, а червячные –
около 15%.
Преимущества и недостатки червячных передач
по сравнению с зубчатыми
Преимущества:
– большие передаточные числа U
U = 10... 60 для силовых передач,
U до 300 (и более) для распределительных передач;
− компактность – по U один червячный редуктор эквивалентен двух-, трехступенчатому зубчатому редуктору;
− плавность и бесшумность работы;
− самоторможение; бывает лишь у однозаходных червячных передач ( < ), двух- и более заходные передачи – несамотормозящие.
Недостатки:
– низкий КПД, у самотормозящих передач < 0,5, у
несамотормозящих – =0,7...0,92 в зависимости от заходности;
– меньшая долговечность как по износу, так и по усталостному выкрашиванию;
– нагревание – следствие компактности и низкого КПД;
– применение дефицитных антифрикционных материалов
для червячных колес (бронзы, латуни).
60
61.
Обозначения (рис. 5.1):– червяк (обычно ВЩ) – P1; n1; d1; S – ход.
Ход соответствует шагу винтовой поверхности и равен
расстоянию, на которое переместится винт вдоль своей оси при
повороте на один оборот;
– червячное колесо (обычно ВМ) – P2; n2; d2; Р – шаг.
Шаг – это расстояние между параллельными сторонами
профиля двух соседних витков червяка, измеренное параллельно оси (обычно по среднему диаметру);
– Z1 – число заходов червяка;
– Z2 – число зубьев колеса.
Рис. 5.1. Схема для определения заходности червяков
Очевидно, что S = Z1 P.
В зависимости от формы внешней поверхности червяка
передачи бывают с цилиндрическим (а) и глобоидным (б) червяком (рис. 5.2).
Рис. 5.2. Схема червячных передач с цилиндрическим (а)
и глобоидным (б) червяком
61
62.
Глобоидная передача имеет повышенный КПД и более высокую (примерно 1,5 раза) несущую способность, но сложна визготовлении и сборке.
В зависимости от формы винтовой поверхности резьбы
цилиндрического червяка передачи бывают с архимедовыми,
конволютными и эвольвентными червяками.
Угол между боковыми сторонами профиля витка у стандартных червяков 2 = 40о.
У червячной передачи (рис. 5.3) оси червяка и колеса взаимно перпендикулярны (точнее, оси скрещиваются в пространстве под прямым углом).
Рис. 5.3. Схема червячной передачи
Окружная скорость на червяке: V1
Окружная скорость на колесе: V2
d1n1
(м/с).
60
d 2 n2
(м/с).
60
Последней скорости (V2) соответствует на червяке скорость
d n Sn
поступательного движения витков V2 = V0, т.е. 2 2 1 ,
60
60
62
63.
откуда передаточное число червячной передачи:n d
U 1 2.
(5.1)
n2
S
Полученная формула неудобна на практике, поэтому преобразуем ее по двум вариантам.
n
Z
1. Поскольку d2 = Z2P и S = Z1P, то U 1 2 .
(5.2)
n2 Z1
Следовательно, заходность червяка играет роль числа его
зубьев.
Из формулы (5.2) следует, что
Z2 = U Z1 Zmin = 30(28) зубьев.
(5.3)
Следовательно, при U = 10 может быть Z1 3;
при U = 15 может быть Z1 2;
при U = 30 может быть Z1 1.
Число заходов червяка можно выбирать из следующей
таблицы:
U
Z1
8…14
4
14…30
2
>30
1
У колеса Z2max = 70…80 зубьев, иначе передача получается
громоздкой.
Оптимальное значение Z2 = 50…60 зубьев.
Рис. 5.4. Угол подъема линии витка на червяке
63
64.
2. Полагаем по формуле (5.1) S = πd1 tg (рис. 5.4), получим:U
n1
d
2 .
n2 d1tg
Следовательно, в червячной передаче U
(5.4)
d2
.
d1
Из формулы (5.4) следует, что d2 n2 = d1 n1 tg .
Умножая обе части на , получим: V2 = V1 tg ,
60
где – угол подъема линии витка на червяке (равный углу наклона зубьев на колесе);
Угол всегда меньше 45o, значит V2 < V1 и эти скорости
взаимно перпендикулярны.
Рис. 5.5. Определение скорости скольжения в червячной передаче
Геометрическая сумма скоростей или скорость скольжения витков червяка по зубьям колеса определяется по формуле
(рис. 5.5):
V
Vск V12 V22 1 .
(5.5)
cos
Эта скорость в червячной передаче может быть весьма
значительной и обуславливать заедание. Поэтому при стальном
червяке обод червячного колеса никогда не делают тоже из стали, а либо из бронзы, либо из латуни, либо из чугуна:
− из чугуна при Vск 2 м/с;
64
65.
− из твердой бронзы и латуни (например, алюминиевожелезистая бронза марки БрА9Ж3Л) при Vск 5 м/с;− из мягкой бронзы (например, оловянистые бронзы марок БрОФ 10-1 и БрО10Н1Ф1 и др.) при Vск = 5…25 м/с.
Мягкие бронзы являются лучшим материалом для червячных колес, однако, они дороги и дефицитны. Твердые бронзы
обладают повышенными механическими характеристиками, но
имеют пониженные противозадирные свойства. Их применяют
в паре с твердым, закаленным до HRC = 45…50 шлифованным
и полированным червяком.
При проектном расчете передачи предварительно скорость
скольжения Vск определяется по следующей формуле:
Vск 4,5 10 4 n1 3 T2 .
(5.6)
5.2. Расчет червячных передач на контактные напряжения
Проектный расчет:
aw = 6103
KT2
2
Н
(мм),
(5.7)
полученное значение необходимо округлить до ближайшего
стандартного значения.
Проверочный расчет:
3
Н
5350(q 2 x) Z 2 q 2 x
q 2 x K H T2 H (МПа), (5.8)
Z2
wст
где Z2 – число зубьев колеса;
T2 – вращающий момент на валу колеса (Н·м);
awст – межосевое расстояние;
KН = KН KНV – коэффициент нагрузки;
KНV – коэффициент динамической нагрузки. Его можно принимать KНV = 1,0 при V2 3 м/c; KНV = 1,1… 1,3 при V2 > 3 м/c,
где V2 – окружная скорость червячного колеса.
65
66.
KН – коэффициент концентрации нагрузки по длине зуба.При постоянной нагрузке можно принимать KН = 1.
2a
q w Z 2 – коэффициент диаметра червяка; его округm
ляют до стандартного значения из следующего ряда:
qст = 8; 10; 12,5; 14; 16; 20.
(5.9)
Z2 = Z1 U, а модуль зацепления m предварительно определяют по
формуле:
a
m = (1,4… 1,7) w (мм).
(5.10)
Z2
Полученное значение m необходимо округлить до стандартного
значения из следующего ряда:
mст = 2; 2,5; 3,15; 4; 5; 6,3; 8; 10; 12,5; 16 мм.
(5.11)
Найденное по формуле (5.7) значение межосевого расстояния необходимо округлить до ближайшего стандартного
значения из следующего ряда:
awст = 40; 50; 63; 80; 100; 125; 140; 160; 180; 200; 225;
250;… мм.
(5.12)
Коэффициент смещения инструмента:
aw
(5.13)
X
0,5(q Z 2 ).
m
Значения коэффициента Х должны лежать в пределах:
–1 Х 1.
Если это условие не выполняется, то необходимо изменить
либо m, либо q, либо Z2, либо аw.
Для передач с эвольвентным червяком рекомендуется
Х=0,5.
5.3. Допускаемые контактные напряжения
при расчете червячных передач
Различают два случая.
1. Для мягких оловянных бронз:
Н Но m No (МПа),
N НЕ
66
(5.14)
67.
где Но = (0,75…0,9) в (МПа) – допускаемое контактное напряжение при N0 = 107 циклов; m = 8;в – предел прочности для бронзы при растяжении (МПа).
Большие значения числового коэффициента в формуле
(5.14) для передач с цементованным, шлифованным и полированным червяком с твердостью витков 45 HRC.
Здесь за базовое число циклов нагружения условно принимают N0 = 107, причем кривая выносливости продолжает понижаться и далее до 25 107 циклов (рис. 5.5).
Рис. 5.5. Кривая контактной выносливости для бронз
Следовательно:
– если NHE < 107 циклов, то допускаемое контактное напряжение для червячного колеса
[ ]Н = (0,75…0,9) в (МПа);
(5.15)
– если 107 < NНЕ < 25 107 циклов, то допускаемое контактное напряжение для червячного колеса
7
10
Н (0,75...0,9) в 8
(МПа);
(5.16)
N НЕ
– если NНЕ > 25 107 циклов, то принимают NНЕ = 25 107
циклов и
Н
(0,75...0,9) в
67
8
107
(МПа).
7
25 10
(5.17)
68.
2. Для твердых бронз, латуней и чугунов допускаемыеконтактные напряжения определяют из условия отсутствия заедания, так как для них наклонные участки кривых усталости
короткие, что позволяет выбирать допускаемые напряжения независимо от числа циклов:
Н Но f (Vск ) .
(5.18)
Для бронз и латуней Н = 300 – 25Vск (МПа) при работе в
паре с червяком с твердостью поверхности витков 45HRC.
Эквивалентное число циклов нагружения находят так же,
как и для цилиндрических передач в зависимости от условий
нагружения:
m
T 2
m
T 2
t НЕ t t t ... (час),
T
T
где m = 8.
Суммарное число циклов напряжений:
N НЕ 60 n2 Lh ,
где
Lh t НЕ g L (час).
(5.19)
(5.20)
(5.21)
5.4. Расчет червячных передач на изгиб
Расчет на изгиб зубьев червячного колеса производится по
формуле:
K Ft 2 YF 2 cos
F F 2
F (МПа),
(5.22)
1,3 mcт (qст 2 х)
где Ft2 – окружное усилие на червячном колесе:
2T
Ft 2 = 2 (Н); T2 (Н·м); d2 (м); mст (мм);
d2
YF2 – коэффициент формы зубьев червячного колеса, выбираемый из табл. 5.1 в зависимости от эквивалентного числа
зубьев
Z2
ZV 2
.
(5.23)
3
cos
68
69.
Таблица 5.1Коэффициент формы зубьев червячного колеса YF2
ZV2
YF2
ZV2
YF2
20
1,98
40
1,55
24
1,88
45
1,48
26
1,85
50
1,45
28
1,8
60
1,40
30
1,76
80
1,34
32
1,71
100
1,3
35
1,64
150
1,27
37
1,61
300
1,24
5.5. Допускаемые напряжения изгиба для червячных колес
1. Для бронз Fo 0,25 т 0,08 в (МПа),
(5.24)
где т и в – пределы текучести и прочности для бронзы.
За базовое число циклов при расчете на изгиб принимают
N0 = 106 циклов. Как и при контактных напряжениях, кривые
усталости при изгибе для бронз имеют очень длинные наклонные участки (до 25 107 циклов).
Если NFE 106 циклов и передача нереверсивная, то
σ F σ Fо .
Если 106 < NFE < 25 107 циклов и передача нереверсивная, то
106
(МПа).
F Fo m
N FE
(5.25)
При расчете на изгиб m = 9.
Если NFE > 25 107 циклов и передача нереверсивная, то
принимают NFE = 25 107 циклов и
F Fo
m
106
25 107
(МПа).
2. Для чугунов при нереверсивной передаче:
F 0,22 ви (МПа),
(5.26)
(5.27)
где ви – предел прочности при изгибе.
У чугунов наклонные участки кривых усталости при изгибе очень короткие, и допускаемые напряжения изгиба можно
принимать независимо от числа циклов нагружения.
69
70.
5.6. Проверка червячной передачи на нагревВвиду компактности и низкого КПД проверке на нагревание подвергаются все червячные редукторы, а из зубчатых редукторов только крупные (100 кВт и выше).
Количество теплоты, выделяющейся в непрерывно работающей червячной передаче: Qвыд = 1000(1– )Р1 (Вт),
(5.28)
где – КПД червячного редуктора;
Р1– передаваемая мощность (Вт).
Количество теплоты, отдаваемой редуктором в окружающую среду (теплоотдача): Qотв = К(t – t0)A(1+ ) (Вт),
(5.29)
1,7
где A 20 аw – теплоотдающая поверхность корпуса
(5.30)
редуктора без дна, но с учетом выступающих частей (ребер,
фланцев и др.), (м2).
t C – температура масла в ванне редуктора;
t0 C = 20о С – температура окружающей среды;
К = 12…18 (Вт/м2 оС) – коэффициент теплопередачи;
– коэффициент, учитывающий теплоотдачу через дно в
плиту или раму, на которой стоит редуктор = 0,1…0,3.
Максимально возможная теплоотдача редуктора в окружающую среду:
Qmax = К(tmax – to)A(1 + ) (Вт),
(5.31)
где tmax – максимально допустимая температура масляной ванны редуктора.
Для применяемых индустриальных масел считается допустимым в редукторе tmax 90оС (в зацеплении будет еще выше).
При более высокой температуре масло будет терять вязкость и
даже окисляться.
Если Qвыд < Qmax, то редуктор перегреваться не будет.
Если Qвыд > Qmax, то редуктор будет перегреваться и необходимо:
− применять принудительный воздушный обдув;
− увеличить теплоотводяющую поверхность редуктора А
за счет дополнительного оребрения;
− применить искусственное охлаждение масла в картере
редуктора (змеевик с охлаждающей водой).
70
71.
ЧАСТЬ II. ВАЛЫ. ПОДШИПНИКИ. МУФТЫГлава 6. ВАЛЫ
6.1. Общие сведения
Зубчатые колеса, звездочки, шкивы и другие вращающиеся детали машин устанавливают на валах или осях. Вал отличается от оси тем, что передает вращающий момент от одной детали к другой, а ось не передает. При работе вал испытывает изгиб и кручение, а иногда еще дополнительно растяжение или
сжатие. Оси могут быть неподвижными или вращаться вместе с
насаженными на них деталями.
Валы могут быть прямые, коленчатые и гибкие. В курсе
«Детали машин» рассматриваются только прямые валы. Чаще
всего прямые валы делают ступенчатыми из технологических соображений изготовления и сборки. Опорные участки валов и осей
называются цапфами. Их подразделяют на шипы, шейки и пяты.
Шейкой называют цапфу в средней части вала или оси.
Пятой называют цапфу, воспринимающую осевую нагрузку. В
качестве материалов для валов и осей чаще всего применяют
стали 45 или 40Х после улучшения.
Основными критериями работоспособности валов являются прочность и жесткость. Прочность оценивается коэффициентом запаса прочности при расчете валов и осей на усталость, а
жесткость – прогибом или углом закручивания в соответствующем сечении вала.
Основными расчетными нагрузками являются вращающие
моменты T и изгибающие моменты Мизг.
Вращающий момент определяется:
T = 9550 P (Н·м),
(6.1)
n
где P (кВт) и п (мин-1) – передаваемая валом мощность и частота его вращения.
В проектном расчете наименьший диаметр, через который
передается вращающий момент, определяется следующим образом:
71
72.
d = 140…150 3 P (мм).(6.2)
n
Полученное значение d необходимо округлить до ближайшего значения из стандартного ряда.
При проектировании редукторов если быстроходный вал
редуктора соединяется с валом электродвигателя через муфту,
то диаметр его выходного конца принимают равным
(0,8…1,0)dэ.
(6.3)
Проверочный расчет производится после конструктивной
проработки вала, определения его диаметральных и линейных
размеров и составления расчетной схемы. При определении нагрузок, действующих на валы, необходимо учитывать не только
силы, действующие в зацеплении, но и радиальную силу Fм от
муфты, возникающую вследствие неизбежной несоосности соединяемых валов. Эта сила для входных и выходных концов
одноступенчатых редукторов может быть приближенно определена*:
Fм ≈ 125 T (Н),
(6.4)
а для выходных валов многоступенчатых редукторов:
Fм ≈ 250 T (Н).
(6.5)
Поскольку направление силы Fм не определено, то при
расчете следует направить ее таким образом, чтобы она увеличивала бы нагрузку на вал от сил в зацеплении, т.е. нужно рассматривать наиболее неблагоприятный случай нагружения.
Нагрузки на валы от клиноременных и цепных передач
определяются при расчете этих передач, однако приближенно
они могут быть определены по формулам (6.4) и (6.5).
*
Для определения радиальной силы Fм от муфты на быстроходном валу редуктора общего машиностроения рекомендуется формула [4]:
Fм = (50…125) T1 (Н)
72
73.
6.2. Расчет валов на статическую прочностьРасчет необходимо произвести, чтобы убедиться в отсутствии пластических деформаций во время пусковых перегрузок.
При расчете в каждом из рассматриваемых сечений валов
определяют нормальные и касательные напряжения при действии максимальных нагрузок. Максимальные нормальные и касательные напряжения определяют по формулам:
М изг mах 103
(МПа),
(6.6)
изг mах =
Wизг
Tmах 103
(МПа),
(6.7)
mах =
Wкр
(6.8)
сж (раст) = F a max (МПа),
A
(6.9)
mах = изг mах + сж(раст) (МПа),
где Мизг mах = Кпуск М х 2 М у 2 – максимальный
(6.10)
изгибающий момент в период пуска (Н·м); Кпуск – коэффициент
T
пусковой перегрузки, равный отношению пуск ;
T
Тmах = Кпуск· Т – максимальный крутящий момент
(6.11)
на валу (Н·м), а Т – номинальный крутящий момент на валу (Н·м);
Fa mах = Кпуск · Fa – максимальная осевая сила (в косозубых и
червячных передачах) (Н);
(6.12)
A – площадь рассматриваемого поперечного сечения вала, (мм2).
Площадь поперечного сечения для вала с одним шпоночным пазом определяется следующим образом:
2
А = d – b t1 (мм2);
4
Wизг – момент сопротивления сечения вала при изгибе (мм3).
Момент сопротивления изгибу для сечения вала со шпоночным пазом определяют по формуле:
73
74.
d 3 bt1 d t1 2bt1 d t1 2
3
Wизг =
= 0,1d –
(мм3).
(6.13)
32
2d
2d
Момент сопротивления кручению для сечения вала со
шпоночным пазом определяют по формуле:
d 3 bt1 d t1 2
bt1 d t1 2
3
Wкр =
= 0,2d –
(мм3), (6.14)
16
2d
2d
где d – диаметр вала в рассматриваемом сечении;
b – ширина шпонки;
t1 – глубина шпоночного паза у вала.
Коэффициент запаса прочности по нормальным напряжениям:
σ
STσ = т ,
(6.15)
σ mах
а коэффициент запаса прочности по касательным напряжениям:
τ
STτ = Т .
(6.16)
τ mах
Общий коэффициент запаса прочности по пределу текучести определяют по формуле:
ST ST
SТ =
ST ,
(6.17)
2
2
ST ST
[SТ] = 1,5…2.
Расчет на статическую прочность можно также производить и по эквивалентному напряжению:
экв u2 3 2 ,
M
М
T
где 0,8 T , u изг изг ,
T 3 – для кругWкр 0,2d
Wизг 0,1 d 3
лого сечения.
6.3. Расчет валов на усталостную выносливость
Для каждого из опасных сечений необходимо произвести
расчет на усталостную выносливость.
74
75.
Уравнение усталостной выносливости имеет вид:S S
S=
[S],
(6.18)
2
2
S S
где [S] = 1,5…2 – коэффициент запаса прочности;
S и S – коэффициенты запаса прочности по нормальным и
касательным напряжениям, определяемые по формулам:
1
S
;
(6.19)
K
ψ т
Kd KF
1
S =
,
(6.20)
К
ψ т
Kd K F а
где 1 и 1 – пределы выносливости стали при симметричных
циклах изгиба и кручения.
Значения коэффициентов запаса прочности при расчете
валов получаются сравнительно большие, что объясняется необходимостью обеспечения достаточной жесткости валов как
условий правильной работы зацепления и подшипников.
Вследствие вращения вала напряжения изгиба в различных точках его поперечного сечения изменяются по симметричному циклу (рис. 6.1,а). Напряжения кручения пропорциональны вращающему моменту и изменяются по отнулевому
циклу (рис. 6.1,б).
Рис. 6.1. Циклы нагружения: а) симметричный; б) отнулевой
K и K – эффективные коэффициенты концентрации напряжений при изгибе и кручении.
При действии в рассматриваемом сечении нескольких источников концентрации напряжений в расчет принимаются
наибольшие значения K и K .
75
76.
Кd – масштабный фактор, выбираемый в зависимости отматериала и диаметральных размеров валов.
Коэффициент КF учитывает влияние шероховатости поверхности, его можно принимать КF = 0,9 0,97, причем при
тонком шлифовании КF = 0,93 0,97, а при чистовом КF = 0,9
0,93. Коэффициенты чувствительности к асимметрии цикла
нагружений ψ и ψ выбирают из таблиц.
– амплитуда циклов нормальных напряжений, равная
наибольшим значениям напряжений изг во время работы:
М изг 103
= u =
(МПа),
(6.21)
Wизг
– амплитуда циклов касательных напряжений, величину которой определяют по формуле:
= T МПа или =0,5 ,
(6.22)
2Wкр
где Мизг и Т – изгибающий и крутящий моменты, действующие
в соответствующем сечении вала.
При нереверсивной работе редуктора т – среднее напряжение цикла нормальных напряжений – можно принимать т = 0.
т – среднее напряжение цикла касательных напряжений
определяют по формуле:
т 0,5 .
(6.23)
6.4. Расчет валов на жесткость
Прогиб вала от действия сил Ft и Fr в среднем между опорами сечения вала (рис. 6.2):
Fr l 3
Ft l 3
(мм); y F
(мм);
yF
48EI
t 48 E I
r
4
I d ,
64
где Е – модуль упругости материала вала;
I – момент инерции круглого сечения, мм4.
76
(6.24)
(6.25)
77.
Рис. 6.2. К определению суммарного прогибаСуммарный прогиб y =
y F2 y F2 [ y] .
t
r
(6.26)
Допускаемый прогиб принимается:
[y] 0,01 m – для цилиндрических передач;
[y] 0,005 m – для конических и червячных передач,
где m – модуль передачи, мм.
Глава 7. ПОДШИПНИКИ
7.1. Общие сведения
Подшипники служат опорами валов и осей, обеспечивая
им возможность свободного вращения или качания и восприятия действующих на них нагрузок.
По виду трения разделяют подшипники скольжения и
подшипники качения, причем подшипники качения являются
основными видами опор, применяемых в машинах.
Подшипники скольжения – это опоры вращающихся деталей, работающие в условиях относительного скольжения поверхности цапфы по поверхности подшипника, разделенных
слоем смазки.
Применение подшипников качения позволило заменить
трение скольжения трением качения. Подшипники качения –
это группа деталей, наиболее широко стандартизованных в мировом масштабе и централизованно изготавливаемых на специальных заводах в массовом количестве. Так, например, ежегод77
78.
ный выпуск подшипников качения в России составляет около1 млрд. штук, 15 тыс. типоразмеров.
В приборах применяют шарикоподшипники с наружным
диаметром 1 мм и диаметром шариков 0,35 мм; в тяжелом машиностроении – подшипники диаметром несколько метров
(2,5 м) с шариками диаметром 203 мм, весом 6,3 т (и даже до 7 т).
Подшипники подразделяют на следующие виды.
1. По форме тел качения – на шариковые и роликовые. Роликоподшипники в свою очередь подразделяют на подшипники
– с цилиндрическими роликами (короткими и длинными)
– с коническими роликами
– с бочкообразными роликами
– с витыми роликами
– с игольчатыми роликами
2. По направлению воспринимаемой нагрузки:
− радиальные – воспринимают только радиальную нагрузку (например цилиндрические роликоподшипники) или радиальную и некоторую осевую (например шарикоподшипники);
− упорные – воспринимают только осевую нагрузку;
− радиально-упорные – воспринимают комбинированную
радиальную и осевую нагрузку;
78
79.
− упорно-радиальные – воспринимают осевую нагрузку инекоторую радиальную.
3. По признаку самоустанавливаемости:
− несамоустанавливающиеся – все шарико- и роликоподшипники (кроме сферических);
− самоустанавливающиеся – сферические подшипники.
4. По габаритным размерам подшипники подразделяют на
размерные серии.
По диаметру
По ширине
сверхлегкие
узкие
особолегкие
нормальные
легкие
широкие
средние
особо широкие
тяжелые
Основное распространение получили легкие и средние узкие серии подшипников.
7.2. Достоинства и недостатки подшипников качения
в сравнении с подшипниками скольжения
Достоинства:
− взаимозаменяемость и возможность изготовления в
массовых количествах на ГПЗ как стандартные изделия, что
значительно снижает стоимость производства;
− меньший расход смазочных материалов, меньшие требования к уходу и меньший нагрев;
− меньшие габариты по ширине, а следовательно, большая несущая способность подшипника;
− меньший расход цветных металлов.
Недостатки:
− повышенные диаметральные размеры;
− хуже воспринимают переменные и, особенно, ударные
нагрузки (причем в этом случае роликоподшипники имеют
преимущества перед шарикоподшипниками);
− высокие контактные напряжения и, следовательно, ограниченный срок службы;
79
80.
− неприменимость подшипников качения в ряде случаевввиду их неразъемности (например, на коленчатых валах);
− невозможность уменьшения зазоров при износе, а следовательно, невозможность применения в особо точных станках
(например, в шлифовальных).
7.3. Основные типы подшипников качения
и их характеристики
Шариковый радиальный однорядный подшипник состоит
из следующих деталей (рис. 7.1):
1 – наружное кольцо;
2 – внутреннее кольцо;
3 – тела качения (шарики);
4 – сепаратор;
d – внутренний диаметр подшипника
(диаметр отверстия);
D – наружный диаметр подшипника;
В – ширина подшипника;
r – размеры фасок.
Рис. 7.1. Шарикоподшипник радиальный однорядный
Предназначен в основном для восприятия радиальных нагрузок, но может воспринимать и некоторые осевые нагрузки (до
70% неиспользованной допустимой радиальной нагрузки).
Подшипник обычно выполняют со стальным штампованным (змейковым) сепаратором, состоящим из двух половин, соединенных заклепками. Назначение сепаратора – удерживать шарики на одинаковом расстоянии (чтобы они не сбивались в одну
сторону).
Радиальный однорядный шарикоподшипник фиксирует осевое положение вала в обе стороны. Количество конструктивных
разновидностей этого типа подшипников значительно. Весьма
80
81.
разнообразны и конструкции сепаратов. При проектировании новых машин в первую очередь следует ориентироваться на применение шариковых радиальных подшипников в связи с их невысокой стоимостью, простотой монтажа и способностью воспринимать комбинированные нагрузки.Шариковый радиальный двухрядный сферический (самоустанавливающийся) подшипник предназначен для восприятия
радиальных нагрузок (рис. 7.2).
Подшипник допускает малую осевую нагрузку. Дорожку
качения наружного кольца выполняют по сферической поверхности, описанной из центра подшипника, что обеспечивает
подшипнику самоустанавливаемость. Подшипники фиксируют
вал (корпус) в осевом направлении в обе стороны.
Рис. 7.2. Шарикоподшипник радиальный двухрядный сферический
Роликовый радиальный с короткими роликами предназначен для восприятия больших радиальных нагрузок (рис. 7.3).
Грузоподъемность в 1,7 раза больше грузоподъемности однорядного радиального шарикового подшипника. Легко разбирается в осевом направлении. Допускает некоторое взаимное
смещение колец, а потому удобен в случаях больших температурных деформаций валов, а также при необходимости осевой
самоустановки валов, например, при шевронных зубчатых колесах. Требует точной соосности посадочных мест.
81
82.
Рис. 7.3. Роликоподшипник радиальныйс короткими цилиндрическими роликами
Роликовый радиально-упорный конический (рис. 7.4)
= 11°…15° – особо легкая серия
= 12°…16° – легкая серия
= 10°…14° – средняя серия
Таким образом, обычно = 1°…16°.
Для восприятия больших осевых нагрузок = 25°…30°.
Угол конусности роликов 1,5°…2,0°.
Рис. 7.4. Роликоподшипник радиально-упорный конический
82
83.
Конические роликоподшипники предназначены для восприятия значительных совместно действующих радиальных иодносторонне действующих осевых нагрузок при средних и
низких скоростях вращения (обычно до 15 м/с).
Радиальная грузоподъемность в среднем в 1,9 раза выше,
чем грузоподъемность радиального однорядного шарикоподшипника.
Отличается удобством сборки и разборки, регулировки зазоров и компенсации износа.
Выполняют обычно с чашечными штампованными сепараторами. При сборке требует регулировки.
Шариковый упорный однорядный подшипник предназначен для восприятия односторонних осевых нагрузок (рис. 7.5).
Рис. 7.5. Шарикоподшипник упорный однорядный
Шариковый радиально-упорный (рис. 7.6)
– угол контакта, = 12°, 26°, 36°.
Отличается большим радиальным зазором. При сборке
требует регулировки.
Рис. 7.6. Шарикоподшипник радиально-упорный
83
84.
7.4. Условные обозначения подшипников каченияУсловные обозначения применяют для маркировки подшипников качения и характеризуют:
− внутренний диаметр;
− серию;
− тип подшипника;
− конструктивные особенности.
Обозначения этих параметров состоят из цифр и букв.
Первая и вторая цифры справа условного обозначения
для подшипников с внутренним диаметром от 20 до 495 мм являются частным от деления внутреннего диаметра подшипника
на цифру пять.
Третья цифра справа обозначает серию:
1 – особо легкая серия;
2 – легкая серия;
3 – средняя серия;
4 – тяжелая серия;
5 – легкая широкая серия;
6 – средняя широкая серия;
8, 9 – сверхлегкие серии.
Четвертая цифра справа обозначает тип подшипника:
0 – радиальный однорядный шарикоподшипник;
1 – радиальный шариковый сферический;
2 – радиальный цилиндрический роликоподшипник с короткими роликами;
3 – радиальный роликовый сферический;
4 – радиальный роликовый с длинными цилиндрическими
роликами или игольчатый;
5 – радиальный роликовый с витыми роликами;
6 – радиально-упорный шариковый;
7 – конический роликоподшипник;
8 – упорный шариковый;
9 – упорный роликовый.
Пятая, шестая и седьмая цифры справа обозначают
конструктивные особенности подшипников. Например, наличие
встроенных уплотнений, стопорной канавки и т.д.
84
85.
Для подшипников с внутренними диаметрами от 10 до 17 ммпредусмотрено следующее обозначение:
Внутренний
диаметр, мм
10
12
15
17
Две последние
цифры справа
00
01
02
03
Буквами обозначают отличительные признаки подшипников,
например:
Х – из цементуемых сталей;
Ю – все детали подшипника из нержавеющей стали;
Р – все детали подшипника из теплостойких сталей;
Л – сепаратор из латуни.
Примеры условных обозначений подшипников качения
Подшипник 206:
– внутренний диаметр 06 · 5 = 30 мм,
цифра 2 обозначает, что подшипник легкой серии.
Подшипник 307:
– внутренний диаметр 07 · 5 = 35 мм,
цифра 3 обозначает, что подшипник средней серии.
Подшипник 4-36209Р:
− шариковый, радиально-упорный, однорядный;
− легкой серии;
− серии ширины 0, с внутренним диаметром 09 · 5 = 45 мм;
− класс точности 4;
− детали подшипника изготовлены из теплостойких сталей.
7.5. Основные критерии работоспособности и расчета
подшипников качения
Для подшипников качения характерными являются следующие основные причины потери работоспособности:
85
86.
усталостное выкрашивание рабочей поверхности;износ колец и тел качения;
разрушение сепараторов;
образование вмятин (бринеллирование) на рабочих поверхностях при динамических нагрузках и при больших
статических нагрузках;
− раскалывание колец и тел качения.
−
−
−
−
7.6. Расчет подшипников качения на долговечность
Подшипники качения работают и рассчитываются на контактные напряжения. Однако этот расчет производится только
при проектировании новых типоразмеров подшипников или нестандартных подшипников качения.
В конструкторской практике то, что обычно называют
расчетом, является лишь подбором подшипников по каталогамсправочникам для определенных условий работы.
Подбор подшипников производится по динамической грузоподъемности С, исходя из действующих радиальных и осевых
нагрузок с учетом условий нагружения и расчетного срока
службы подшипников.
Величина С является основной характеристикой подшипника и приводится в каталогах. В каталогах указаны основные
размеры подшипников, динамическая грузоподъемность С, статическая грузоподъемность С0, предельная частота вращения п.
Под номинальной долговечностью понимают срок службы
подшипников, в течение которого не менее 90% из данной
группы при одинаковых условиях должны проработать без появления признаков усталости металла.
Долговечность конкретного подшипника зависит как от
внешних факторов (величины и направления усилий, числа
оборотов, смазки и т.п.), так и от его динамической грузоподъемности.
Расчет подшипников по долговечности L производится
при п > 10 мин-1, но не превышающем предельного числа оборотов для данного подшипника.
86
87.
Долговечность подшипников определяется по эмпирической зависимости, полученной на основании экспериментальных работ.C
L = a23 (млн. оборотов), или С = P L (Н),
(7.1)
a23
P
где α – показатель степени;
α = 3 – для шарикоподшипников;
α = 3,33 – для роликоподшипников;
С – динамическая грузоподъемность подшипников (кН);
P – расчетная эквивалентная нагрузка (кН).
Для условий работы, отличающихся от нормальных, определяют скорректированный расчетный ресурс с учетом уровня
требуемой надежности, специальных свойств и конкретных условий эксплуатации.
а1 – коэффициент надежности:
при Р = 90% а1 = 1;
при Р = 95% а1 = 0,62;
при Р = 97% а1 = 0,44;
при Р = 99% а1 = 0,21.
а2 – коэффициент, корректирующий ресурс в зависимости
от особых свойств металла и (или) конструкции подшипника.
а3 – коэффициент смазки, корректирующий ресурс в зависимости от условий работы подшипников.
Под особыми свойствами металла понимают обычную
плавку, вакуумный или электрошлаковый переплав, химический состав, наличие специальной очистки металла от неметаллических включений.
Под особыми условиями эксплуатации понимают перекосы
колец, наличие гидродинамической пленки масла в контакте колец и тел качения, вакуум, радиацию, агрессивные среды и т.д.
Ввиду того, что коэффициенты а2 и а3 взаимосвязаны, в
настоящее время в расчетах принято использовать их произведение: а23 = а2 а3.
a23 = 0,7…0,8 – для шарикоподшипников;
a23 = 0,6…0,7 – для роликоподшипников конических;
a23 = 0,5…0,6 – для роликоподшипников цилиндрических и
сферических двухрядных шарикоподшипников.
В курсовых проектах можно принимать а1 = 1, а2 = 1, а3 = 1.
87
88.
Долговечность подшипников может быть выражена и в часах:6
6
Lh = a23 10 L a23 10 C ≥ Lhзад (часов),
(7.2)
60n
60n P
где п – частота вращения подшипника;
если число оборотов п = 1…10 мин–1, то расчет ведется для
п = 10 мин–1;
если п < 1 мин–1, то действующая нагрузка рассматривается как статическая и при выборе подшипника сравнивается со
статической грузоподъемностью С0 для данного типоразмера
подшипника.
7.7. Определение эквивалентной нагрузки
Эквивалентной нагрузкой Р для радиальных и радиальноупорных подшипников называется такая постоянная нагрузка,
которая при приложении к подшипнику с вращающимся внутренним кольцом и неподвижным наружным обеспечивает такую же долговечность, какую подшипник будет иметь при действительных условиях нагружения и вращения.
Эквивалентная нагрузка для однорядных радиальных шарикоподшипников и однорядных радиально-упорных шарико- и роликоподшипников определяется по следующей зависимости:
Рr = (Х ∙ Fr ∙ V + Y ∙ Fa) ∙ Kδ ∙ KТ (Н)
(7.3)
Fa
при соотношении
> е;
V Fr
Рr = Х ∙ Fr ∙ V ∙ Kδ ∙ KТ (Н)
(7.4)
Fa
при соотношении
≤ е,
V Fr
где Fr– радиальная нагрузка на подшипник (Н);
Fa– осевая нагрузка на подшипник (Н);
Х – коэффициент радиальной нагрузки;
Y – коэффициент осевой нагрузки;
V – коэффициент вращения кольца
V = 1 при вращении внутреннего кольца,
V = 1,2 при вращении наружного кольца;
Kδ – коэффициент безопасности
Kδ = 1 при спокойной нагрузке,
88
89.
Kδ = 1,2 при легких толчках, для редукторов обычно выбирают Kδ =1,3…1,5;KТ – температурный коэффициент
KТ = 1 при Т< 100°С,
KТ = 1,05…1,4 при Т = 125°С…250°С;
е – коэффициент осевого нагружения.
Приведенная нагрузка для упорных подшипников:
Ра = Fa ∙ Kδ ∙ KТ.
(7.5)
При расчете радиально-упорных подшипников необходимо учитывать, что в них при радиальном нагружении и отсутствии осевого зазора и натяга возникает осевая сила S, принимаемая равной:
– для шарикоподшипников S = e ∙ R;
– для роликоподшипников S = 0,83 ∙ e ∙ R,
где коэффициент 0,83 связан с законом распределения нагрузки
между телами качения роликоподшипников.
Таким образом, расчетная осевая нагрузка на подшипник
складывается из внешней нагрузки на вал и осевой составляющей от другого радиально-упорного подшипника вала.
При переменной нагрузке
Pi3 Li 3 P13 L1 P23 L2 ...
3
Р =
,
(7.6)
L
Li
где P1 и Р2 – постоянная нагрузка, действующая в течение заданного срока работы;
L1 и L2 – млн. об.;
L – общий ресурс млн. об. за весь срок службы.
Если продолжительность работы на каждом режиме Lhi задана в часах, то ее пересчитывают в млн. об.:
60 ni Lhi
Li =
.
(7.7)
106
Если в результате расчета оказалось, что Lh намного превышает Lhзад , то рекомендуется выбрать подшипник более легкой серии; если же наоборот, Lh < Lhзад , то нужно выбрать
подшипник более тяжелой серии или большего размера.
89
90.
7.8. Материалы, применяемые для изготовленияподшипников качения
Основными материалами для колец и тел качения подшипников являются шарикоподшипниковые высокоуглеродистые хромистые стали ШХ15, ШХ15СГ. Также широко применяются цементуемые стали 18ХГТ, 20Х2Н4А и др.
Твердость колец обычно НRC 60…65, шариков – НRC
62…66.
Сепараторы массовых подшипников изготавливают из углеродистой стали методом штамповки, для высокоскоростных
подшипников применяют массивные сепараторы из антифрикционных бронз, аннодированного дюралюмина, полиамидов и др.
7.9. Смазка подшипников качения
Для смазки подшипников качения применяют в основном
два вида смазочных материалов:
а) жидкие минеральные масла;
б) пластические смазки.
Выбор смазочного материала того или иного вида должен
производиться с учетом конструкции подшипникового узла,
типоразмера подшипника и режима его работы (температура,
влажность, наличие агрессивной среды и т.д.).
Пластические смазки:
– солидол (для температур –30…+70°С);
– натриево-кальциевая смазка 1–13 (для температур
–20…+110°С).
Для работы в диапазоне повышенных температур (в частности, для герметизированных подшипников) применяют смазки:
– ЦИАТИМ 201 (–60…+90°С);
– ЦИАТИМ 203 (–50…+100°С);
– Литол 24.
В качестве смазочных масел для смазывания подшипников
качения применяют обычно минеральные (нефтяные) масла.
Жидкие смазки применяют при необходимости минимальных потерь на трение и при высоких температурах.
90
91.
Допустимая рабочая температура подшипников при жидкой смазке до 120°С, а в отдельных случаях до 150°С и выше(автотракторное АК-10, АК-15).
Применяют следующие способы смазки жидкими маслами:
– Смазку окунанием в масляную ванну – для подшипников
горизонтальных валов при п ≤ 1000 мин–1 уровень масла должен
быть не выше центра нижнего шарика, а при п > 3000 мин–1 –
еще ниже.
– Смазку разбрызгиванием из общей масляной ванны узла.
– Смазку масляными туманами – для особо быстроходных
подшипников при п = 30000…45000 мин–1.
7.10. Посадки подшипников качения (рис. 7.7)
H7 H7
H7 H7
– прямозубые
– косозубые
p6 r 6
r6 S 6
Рис. 7.7. Схема посадок на валу редуктора
91
92.
Глава 8. МУФТЫМуфты применяются для соединения соосных валов и передачи вращающего момента. Кроме того, некоторые типы
муфт могут выполнять и другие функции – например, включать
и выключать исполнительный механизм без выключения двигателя, включать отдельные участки валов, предохранять от перегрузки или от разрушения приводной механизм, компенсировать ряд несоосностей соединяемых валов. К таким несоосностям относятся:
– раздвижка валов (осевое смещение)
– радиальное смещение валов
– угловое смещение валов
Многообразие требований, предъявляемых к муфтам, и
различные условия их работы обусловили создание большого
количества конструкций муфт, к которым относятся:
– муфты механические;
– муфты электромагнитные;
– муфты гидравлические.
В курсе «Детали машин» рассматривают механические
муфты.
92
93.
8.1. Классификация механических муфтПо принципу действия:
– постоянные муфты, осуществляющие постоянное соединение валов между собой;
– сцепные муфты, допускающие во время работы сцепление и расцепление валов с помощью системы управления;
– самоуправляемые муфты, автоматически разъединяющие
валы при изменении заданного режима работы машины.
По характеру работы:
– жесткие муфты, передающие вместе с вращающим моментом вибрации, толчки и удары;
– упругие муфты, амортизирующие вибрации, толчки и удары при передаче вращающего момента благодаря наличию упругих элементов – различных пружин, резиновых втулок и др.
Основной характеристикой муфт является передаваемый
вращающий момент Т.
Глухие муфты
Глухие муфты соединяют соосные валы в одну жесткую
линию. Относятся к постоянным муфтам. Применяются в тихоходных приводах. Из различных видов глухих муфт наибольшее распространение получили втулочная и фланцевая муфты
(рис. 8.1).
Втулочная муфта представляет собой втулку, насаживаемую на концы валов. Применяется для передачи небольших
вращающих моментов. Имеет простую конструкцию, малые габариты и низкую стоимость. Недостатком муфты является неудобный монтаж и демонтаж, связанные с осевым смещением
валов или муфты вдоль вала. Материал втулки – сталь 45.
Втулочная муфта
Фланцевая муфта
Рис. 8.1. Глухие муфты
93
94.
Фланцевая муфта состоит из двух полумуфт с фланцами,стянутыми болтами, причем половина болтов установлена с зазором, а другая без зазора.
Фланцевые муфты просты по конструкции, надежны в работе, могут передавать большие моменты.
Жесткие компенсирующие муфты
Жесткие компенсирующие муфты относятся к постоянным
муфтам и предназначены для соединения валов с компенсацией
радиальных, осевых и угловых смещений вследствие неточности изготовления и монтажа.
Компенсация отклонений от соосности валов достигается за
счет подвижности жестких деталей муфты. Эти муфты уменьшают дополнительные нагрузки на валы и подшипники, вызываемые отклонениями от соосности валов. Наибольшее распространение из группы компенсирующих муфт получили зубчатые и цепные (рис. 8.2; 8.3).
Зубчатая муфта состоит из двух обойм (1) с внутренними
зубьями эвольвентного профиля, которые зацепляются с зубьями втулок (2), насаживаемых на концы валов. Обоймы соединены между собой болтами, поставленными в отверстия без зазора. Втулки и обоймы изготовляют из стали 40 или стали 45Л.
Зубчатые муфты компенсируют радиальные, осевые и угловые смещения валов за счет боковых зазоров в зацеплении и обточки зубьев втулок по сфере. Компенсация отклонений от соосности валов сопровождается скольжением зубьев. Угол перекоса оси каждой втулки относительно оси обоймы допускается
до 0°30'.
Для повышения износостойкости зубья подвергают термообработке, а муфту заливают маслом большой вязкости, которое меняют через каждые три–четыре месяца.
94
95.
Рис. 8.2. Зубчатая муфта:1 – ведущая полумуфта; 2 – ведомая полумуфта; 3 – уплотнение
Цепная муфта состоит из двух полумуфт-звездочек,
имеющих одинаковые числа зубьев, охватывающей их общей
цепи и защитного кожуха, заполненного пластичным смазочным материалом. Применяются цепи роликовые однорядные и
двухрядные, а также зубчатые.
Достоинства цепных муфт – простота конструкции и обслуживания, относительно небольшие габариты.
Из-за наличия зазоров в шарнирах цепи и в сопряжении ее
со звездочками цепные муфты имеют значительные люфты, поэтому их не применяют в реверсивных приводах (реверс будет
сопровождаться ударами).
Цепные муфты допускают угловое смещение валов α < 1° и
радиальное смещение δ = 0,15…0,7 мм в зависимости от размера муфты.
Рис. 8.3. Цепная муфта
95
96.
8.2. Расчет муфты упругой втулочно-пальцевойИз всего многообразия муфт для соединения вала электродвигателя с быстроходным валом редуктора чаще всего применяют муфты упругие втулочно-пальцевые (МУВП); рис. 8.4.
Эти муфты стандартизированы. Предварительно они подбираются по передаваемому вращающему моменту Т или по диаметру вала d и проверяются на смятие упругого резинового
элемента и на изгиб пальца.
Рис. 8.4. Муфта упругая втулочно-пальцевая
Проверка на смятие:
2 T1 10 3
см
(8.1)
см (МПа);
D1 lв m Z d n
см = 2…4 МПа – для резинового упругого элемента.
Проверка пальцев на изгиб:
2Т1 103 (0,5lвт b)
изг
изг (МПа),
(8.2)
D1 Z 0,1d n3
где Т1 – момент на быстроходном валу редуктора (Н·м);
D1 – диаметр, на котором расположены пальцы (м);
lвт – длина резиновой втулки (мм);
Z – число пальцев;
dn – диаметр пальца (мм);
b – зазор между полумуфтами (мм);
изг выбирают из табл. 8.1.
96
97.
Таблица 8.1Материал для
изготовления пальцев
Сталь 30
Сталь 40
Сталь 50
Термообработка
Нормализация
Улучшение
Нормализация
Улучшение
Нормализация
Улучшение
изг , МПа
120 – 150
140 – 170
140 – 170
160 – 200
150 – 190
280 – 320
8.3. Расчет предохранительной муфты со срезным штифтом
Для соединения тихоходного вала редуктора с валом конвейера обычно применяют комбинированные муфты. Примером
такой муфты может служить муфта, состоящая из МУВП и
муфты со срезным штифтом (рис. 8.5). Эти муфты компактны и
обладают высокой точностью срабатывания. В качестве разрушающего элемента обычно используют штифты, выполненные
из стали 45. Штифты помещают в стальных (обычно изготовленных из стали 40Х), закаленных втулках, имеющих высокую
твердость (НRC = 50–55).
Расчет такой муфты производится на смятие упругого
элемента (формула 8.1), проверяются пальцы на изгиб (формула
8.2) и определяется диаметр срезного штифта:
dшт =
4 103 T2 K 2
8 103 Т 2 К
(мм),
Z D1 ср
Z D1 ср
(8.3)
где Т2 – момент на тихоходном валу редуктора (Н·м);
Z – число штифтов; обычно Z = 1, реже Z = 2;
К – коэффициент случайных колебаний нагрузки; при спокойной работе и небольших разгонных массах (например
приводы конвейеров) можно принимать К = 1,2 … 1,4;
D1 – диаметр, на котором расположен штифт или штифты (м);
ср – предел прочности на срез (например для стали 45
ср = 400 МПа).
Полученный по расчету диаметр штифта округляют до
ближайшего большего целого значения и уточняют диаметр
расположения штифта D1.
97
98.
98Рис. 8.5. Муфта комбинированная со срезным штифтом
99.
ЧАСТЬ III. РЕМЕННЫЕ И ЦЕПНЫЕ ПЕРЕДАЧИГлава 9. РЕМЕННЫЕ ПЕРЕДАЧИ
9.1. Общие сведения
Работа ременной передачи (как и фрикционной) основана
на принципе трения. Силы трения возникают в результате натяжения ремня, создающего на рабочих поверхностях силы
нормального давления.
В зависимости от формы поперечного сечения ремня различают основные виды ременных передач.
1. Плоскоременная передача
2. Клиноременная передача
3. Круглоременная передача
Условно к ременным передачам можно отнести зубчатоременные передачи
99
100.
Основные типы ремней1. Плоские ремни:
а) прорезиненные – наиболее распространенные. Состоят
из нескольких слоев хлопчатобумажной ткани, связанных между собой
вулканизированной резиной;
б) хлопчатобумажные – изготавливаются из цельной ткани
с несколькими слоями основы и утка,
пропитанными специальным составом (битум, озокерит);
в) шерстяные – ткань с многослойной шерстяной основой
и хлопчатобумажным утком, пропитанная специальным составом (сурик
на олифе);
г) кожаные – обладают хорошей тяговой способностью и
высокой долговечностью, хорошо переносят колебания нагрузки, но дефицитны (применяются в приборах и
машинах домашнего обихода);
д) пленочные – новый тип ремней из пластмасс на основе
полиамидных смол, армированных
кордом из капрона или лавсана; толщина 0,4 1,2 мм; применяют в высокоскоростных передачах.
2. Клиновые ремни:
100
101.
Внутри ремней проходит корд (1 или 4), являющийся основным несущим элементом ремня. Корд может быть из ткани(1) или из шнуров (4), поэтому ремни получили соответствующие названия. Корд располагается в зоне нейтрального слоя.
Клиновые ремни изготавливаются в виде замкнутой бесконечной ленты. Эти ремни получили наибольшее распространение.
Применение ременных передач
По мощности – обычно до 50 кВт; уникальные до 2000 кВт.
По скорости – обычно V = 5…10 м/с, уникальные до 100 м/с.
По передаточному числу:
U < 5 – открытые передачи;
U 10 – натяжные передачи.
В комбайне «Дон» применяются 14 ременных передач, из
которых 3 – плоскоременных и 11 – клиноременных, а также 8
цепных передач.
9.2. Классификация ременных передач по способам
натяжения ремня
1. Передачи с периодической перешивкой ремня
2. Натяжные передачи с периодическим подтягиванием
ремня
101
102.
3. Натяжные передачи с постоянным натяжением ремня4. Натяжные передачи с автоматическим натяжением ремня
9.3. Преимущества и недостатки ременных передач
по сравнению с зубчатыми
Преимущества:
− возможность передавать движение на значительном
расстоянии (до 15 м);
− плавность и бесшумность работы;
− возможность работы при высоких скоростях;
− предохранение механизмов от перегрузки и резких колебаний нагрузки за счет возможного проскальзывания
ремня;
− простота конструкции и эксплуатации.
Недостатки:
− повышенные габариты (для одинаковых условий диаметры шкивов примерно в 5 раз больше диаметров зубчатых колес);
− некоторое непостоянство передаточного числа, вызванное скольжением ремня в зависимости от нагрузки;
− нагрузка на валы и опоры;
− малая долговечность ремня.
102
103.
9.4. Силы в ременной передаче и напряжения в ремнеДля создания трения между ремнем и шкивом ремню создают предварительное натяжение силой F0 (рис. 9.1,а).
Рис. 9.1. Силы в ременной передаче
Если передача не передает вращающий момент, т.е. находится в покое или работает на холостом ходу, то ветви ремня
натянуты с одинаковой силой F0. При передаче вращающего
момента происходит перераспределение сил натяжения в ветвях
ремня: ведущая ветвь ремня (ВЩ) натягивается дополнительно
до силы F1 > F0, а натяжение ведомой ветви (ВМ) уменьшается
до F2 (рис. 9.1,б).
Из условия равновесия моментов относительно т. О (рис. 9.1,б):
F d Fd
Мо = 0; T1 2 1 1 1 0 ,
(9.1)
2
2
где Т1 можно представить как T1 Ft
d1
, тогда
2
F1 – F2 = Ft;
F1 + F2 = 2F0;
(9.2)
(9.3)
2 103 T1
Ft
– окружная сила на шкиве, Н.
d1
Соотношение между силами F1 и F2 в работающей передаче можно определить по формуле Л. Эйлера:
F1
e f ,
(9.4)
F2
где е = 2,72 – основание натурального логарифма;
103
104.
f – коэффициент трения между ремнем и шкивом; для прорезиненных ремней можно принимать f = 0,4;– угол обхвата шкива (рад.)
Складывая и вычитая уравнения 9.2 и 9.3 почленно, получаем:
F F F
Ft
Ft
1
2
t
и
F
F
.
(9.5)
F
F
1
0
2
0
2
2
F
F
2
F
1
2
0
При круговом движении ремня по шкиву на него действует центробежная сила
FV 10 6 AV 2 (Н),
(9.6)
где А – площадь сечения ремня (мм2);
– плотность материала ремня (кг/м3);
V – скорость ремня (м/с).
Сила FV ослабляет силу предварительного натяжения F0 и
понижает нагрузочную способность передачи. Однако это
влияние существенно только при больших скоростях.
9.5. Нагрузка на валы и подшипники
Силы натяжения ремня нагружают валы и подшипники, в
которых установлены валы Fв (см. рис. 9.1,а).
Равнодействующая сила Fв сил F0 определяется по формуле:
a
Fв 2 F0 sin 1 (Н),
(9.7)
2
где 1 – угол обхвата ремнем малого шкива (см. ниже ф-лу 9.26).
Обычно сила Fв в 2 3 раза превышает окружную силу Ft,
что является существенным недостатком ременных передач.
9.6. Напряжения в ремне
1. Напряжение 0 от силы предварительного натяжения
F
0 0 (МПа),
(9.8)
A
где А – площадь поперечного сечения ремня (мм2).
104
105.
2. Полезное напряжение t:F
t t (МПа).
A
(9.9)
Так как Ft = F1 – F2, то полезное напряжение в ремне является
разностью напряжений 1 в ведущей и 2 в ведомой ветвях
ремня:
t = 1 – 2.
(9.10)
Величиной t оценивают тяговую способность ременной
передачи.
3. Напряжение изгиба u возникает в ремне при огибании
им шкивов:
h
u = E u
(МПа),
(9.11)
d1
где h – высота сечения ремня (мм);
Eu – модуль продольной упругости ремня (МПа);
d1 – диаметр малого шкива, так как наибольшее напряжение
изгиба возникает на малом шкиве.
Напряжения изгиба являются главной причиной усталостного разрушения ремня.
4. Напряжение от центробежной силы FV:
V pV 2 10 6 (МПа).
(9.12)
Наибольшее напряжение возникает в т. А (рис. 9.2), т.е. в
точке набегания ведущей ветви ремня на малый шкив.
max = 1 + u + V = 0 + 0,5 t + u + V p (МПа),
(9.13)
где 1 (учитывая формулы 9.5) равняется:
1
F0
F
0,5 t 0 0,5 t .
A
A
105
106.
Рис. 9.2. Напряжения в ремне9.7. Тяговая способность и расчет ременных передач.
КПД ременных передач
Основными критериями работоспособности ременных передач являются тяговая способность и долговечность ремня.
Тяговая способность обуславливается прочностью сцепления
ремня со шкивом. Расчет ременных передач по тяговой способности основан на кривых скольжения и КПД (рис. 9.3).
Рис. 9.3. Кривые скольжения и КПД
106
107.
Кривые скольжения и КПД получены экспериментальнымпутем при определенных условиях испытаний: u = 1; V = 10 м/с;
горизонтальное расположение передачи.
На графике по оси ординат откладывают относительное
скольжение % и КПД, а по оси абсцисс – нагрузку передачи,
выраженную через коэффициент тяги:
F
t t .
(9.14)
2 F0 2 0
Из графика видно, что при увеличении до критического
значения 0 наблюдается только упругое скольжение ремня .
Поскольку упругие деформации ремня приближенно подчиняются закону Гука, этот участок близок к прямолинейному. При
дальнейшем увеличении от 0 до max начинается частичное
буксование. Величина 0 называется критическим коэффициентом тяги. Согласно кривым скольжения рабочую нагрузку рекомендуется выбирать вблизи значения 0 и слева от него, которому соответствует ηmax . При нормальных условиях работы
ηmax = 0,95 0,97 – для плоскоременных передач и ηmax = 0,92
0,96 – для клиноременных.
Для плоскоременной передачи оптимальное значение
0 = 0,4 0,6, а для клиноременной 0 = 0,7 0,8.
Определив по кривым скольжения 0, находят допускаемую окружную силу:
F t 2 0 F0 (H) или t 0 2 0 0 (МПа). (9.15)
Рекомендуется принимать:
0 1,5 МПа – для клиновых ремней;
0 1,8 МПа – для плоских ремней.
Переход от типовой передачи к передачам, отличающимся
от типовой, производится с помощью корректирующих коэффициентов С , СV, Cp и С0, где С – коэффициент угла обхвата,
учитывающий снижение тяговой способности передачи с
уменьшением угла обхвата;
СV – скоростной коэффициент, вводимый только для передач без автоматического регулирования натяжения и учиты-
107
108.
вающий уменьшение прижатия ремня к шкиву под действиемцентробежных сил;
Cp – коэффициент режима работы, учитывающий влияние
колебаний нагрузки на долговечность ремня;
С0 – коэффициент, учитывающий способ натяжения ремня
и наклон передачи к горизонту.
Приведенные коэффициенты используют при расчете
плоскоременных передач. При расчете клиноременных передач
используются также коэффициенты Сl и Сu:
Сl – коэффициент длины ремня, который учитывает влияние на долговечность действительной длины ремня l по отношению к базовой длине L0;
Сu – коэффициент передаточного числа.
Долговечность ремня зависит не только от значений напряжений, но и от числа циклов изменения напряжений изгиба.
Полный цикл напряжений соответствует одному пробегу ремня
по шкивам. Число пробегов ремня П (с-1) в секунду определяется по формуле:
V
П П ,
(9.16)
l
где V – скорость ремня (м/с);
l – длина ремня (м);
П – допускаемая частота пробегов (с-1).
Для обеспечения средней долговечности в 2000 3000 часов работы рекомендуется принимать:
П 5 10 с-1 – для плоских ремней;
П 20 с-1 – для клиновых ремней.
Ведущая ветвь, передающая окружное усилие, как было
отмечено выше, натянута больше ведомой. Поскольку ремень
упруго растягивается, то он при переходе с ведущей ветви на
ведомую укорачивается, и происходит это на ведущем шкиве.
На ведомом шкиве ремень удлиняется. В результате окружная
скорость V1 ведущего шкива оказывается больше скорости ремня, а окружная скорость V2 ведомого шкива – меньше нее. Это
происходит в результате упругого скольжения ремня по шкиву,
неизбежного при работе передач трением.
108
109.
9.8. Расчет и проектирование клиноременныхпередач
Исходными данными для расчета являются передаваемая
мощность на ведущем шкиве Р1, частота вращения малого шкива п1 и передаточное число U.
Расчет клиноременной передачи (рис. 9.4) удобно вести в
следующей последовательности.
1. По графику рис. 9.5 выбрать сечение ремня в зависимости от передаваемой мощности Р1 (кВт) и частоты вращения
малого шкива п1 (мин-1) нормального сечения.
Частота вращения
малого шкива n1, мин-1
Рис. 9.4. Передача клиноременная:
1 – малый шкив; 2 – большой шкив; 3 – ремень
Передаваемая мощность Р1, кВт
Рис. 9.5. Выбор сечения клинового ремня нормального сечения
109
110.
2. По таблице 9.1 выбрать минимальное значение диаметра малого шкива d1.Таблица 9.1
Минимальное значение диаметров малых шкивов
Обозначение
сечения
ремня
Вращающий
момент, Н·м
d1 min, мм
Нормального сечения
А
В
15–60
50–150
90
125
С
Узкого сечения
D
120–550 450–2000
200
315
SPА
SPВ
SPС
90–400
300–2000
> 1500
90
140
224
При этом необходимо иметь в виду, что долговечность передачи в значительной степени зависит от диаметра меньшего шкива, поэтому при расчете передачи лучше выбирать не минимальное
значение d1 (мм), а последующее значение из стандартного ряда:
d1,2 = 63; 71; 80; (85); 90; (95); 100; (106); 112; (118);
125; (132); 140; (150); 160; (170); 180; (190); 200;
(9.17)
(212); 224; (236); 250; (265); 280; (300) 315; (335);
355; (375); 400; (425); 450; (475); 500;… мм.
Размеры, указанные в скобках, применяются в технически
обоснованных случаях.
3. Определить диаметр большего шкива d2:
d2 = d1 ∙U (мм).
(9.18)
Полученное значение d2 необходимо округлить до стандартного значения из ряда (9.17).
4. Определить фактическое передаточное число U':
U′ =
d2
U U
; ΔU =
·100% ≤ ± 5%;
d1 1
U
(9.19)
ξ = 0,01–0,02 – коэффициент скольжения при нормальном
режиме работы.
5. Найти ориентировочные значения минимального аmin,
максимального аmax и среднего аср межосевого расстояния:
аmin = 0,55 (d1 + d2) + h (мм);
110
(9.20)
111.
аmax = 2(d1 + d2) (мм);(9.21)
а amax
аср = min
(мм),
(9.22)
2
где h – высота сечения ремня выбирается по табл. 9.11 (мм).
Предварительно необходимо выбрать значение а, близкое
к значению аср.
6. Определить расчетную длину ремня lр′:
(d 2 d1 ) 2
lр' = 2aср + 0,5 π(d1 + d2) +
(мм).
(9.23)
4a
Полученное значение l′ (мм) необходимо округлить до
стандартного значения из следующего ряда:
l = 400; 450; 500;560; 630; 710; 800; 900: 1000; 1120; 1250;
1400; 1600; 1800; 2000; 2240; 2500; 2800; 3150; 3550;
4000; 4500;… мм.
(9.24)
7. Определить уточненное значение межосевого расстояния а:
а = 0,125{2l – π(d2 + d1) +
+
2l d 2 d1 2 8 d 2 d1 2 } мм.
(9.25)
8. Определить угол обхвата ремнем малого шкива α1 :
α1 = 180 – 57
d 2 d1
.
a
(9.26)
Угол α1 должен быть более 120 .
9. Определить скорость ремня V:
d1n1
(м/с).
60 1000
10. Определить частоту пробегов ремня П:
V=
П=
V -1
(с ),
l
причем для клиновых ремней [П] ≤ 20 с-1.
111
(9.27)
(9.28)
112.
Если частота пробегов ремня П оказывается больше допустимого значения, то выбирают большую длину ремня из ряда (9.24) и находят новое значение межосевого расстояния а.Выполнение условия П ≤ [П] обеспечивает долговечность
ремней.
11. Определить допускаемую мощность, передаваемую
одним ремнем с учетом условий эксплуатации:
[Р] =
P0 C Cl CU
(кВт),
Ср
(9.29)
где Р0 – номинальная мощность, передаваемая одним ремнем в
условиях типовой передачи (т.е. α1 = 180 ; U = 1) при спокойной нагрузке и базовой длине ремня L0, которую выбирают по
табл. 9.2 для клиновых ремней нормального сечения, а по
табл. 9.3 – для клиновых ремней узкого сечения.
Таблица 9.2
Номинальная мощность (Р0, кВт), передаваемая одним клиновым
ремнем нормального сечения
Сечение ремня
А
(L0 = 1700 мм)
В
(L0 = 2240 мм)
С
(L0 = 3750 мм)
Диаметр
малого
шкива
d1, мм
90
100
112
125
125
140
160
180
200
224
250
280
Скорость ремня V, м/с
5
10
15
20
25
0,84
0,95
1,05
1,15
1,39
1,61
1,83
2,01
2,77
3,15
3,48
3,78
1,39
1,60
1,82
2,00
2,26
2,70
3,15
3,51
4,59
5,35
6,02
6,63
1,75
2,07
2,39
2,66
2,80
3,45
4,13
4,66
5,80
6,95
7,94
8,86
1,88
2,31
2,74
3,10
–
3,83
4,73
5,44
6,33
7,86
9,18
10,4
–
2,29
2,82
3,27
–
–
4,88
5,76
–
7,95
9,60
11,1
112
113.
Таблица 9.3Номинальная мощность (Р0, кВт), передаваемая одним
клиновым ремнем узкого сечения
Диаметр
малого шкива
d1, мм
90
100
112
140
160
180
Сечение ремня
SPA
(L0 = 2500 мм)
SPB
(L0 = 3550 мм)
Скорость ремня V, м/с
5
10
15
20
1,56
1,89
2,17
2,95
3,54
3,80
2,57
3,15
3,72
5,00
5,98
6,70
–
4,04
4,88
6,37
7,88
9,05
–
4,46
5,61
–
9,10
10,6
Сα – коэффициент угла обхвата; его выбирают по табл. 9.4 в зависимости от угла обхвата α1 малого шкива.
Таблица 9.4
Значение Сα для клиновых ремней
α1
Сα
180
1
170
0,98
160
0,95
150
0,92
140
0,89
130
0,86
120
0,82
110
0,78
Cl – коэффициент длины ремня, который учитывает влияние на долговечность действительной длины ремня l по отношению к базовой длине L0. Его выбирают по табл. 9.5.
Таблица 9.5
Значение коэффициента длины ремня Сl
Отношение l
L0
Для клинового ремня
нормального сечения
Для клинового ремня
узкого сечения
0,4
0,6
0,8
1,0
1,2
1,4
1,6
0,82
0,89
0,95
1
1,04
1,07
1,10
0,85
0,91
0,96
1
1,03
1,06
1,08
СU – коэффициент передаточного числа U; его выбирают по
табл. 9.6.
113
114.
Таблица 9.6Значение коэффициента передаточного числа CU
U
1
1,2
1,4
1,8
СU
1,0
1,07
1,1
1,12
2,5
и выше
1,14
Ср – коэффициент режима работы; его выбирают по табл. 9.7.
Таблица 9.7
Режим
работы
Ср
Легкий
Средний
Тяжелый
1,0–1,2
1,1–1,3
1,3–1,5
Весьма
тяжелый
1,5–1,7
Работа ленточных конвейеров относится к легким режимам; работа цепных конвейеров – к средним режимам; винтовых и скребковых – к тяжелым; экскаваторы, прессы, молоты
работают в весьма тяжелом режиме.
12. Определить необходимое число ремней:
Z=
P1
,
P C z
(9.30)
где Сz – коэффициент неравномерности распределения нагрузки
между ремнями; его выбирают по табл. 9.8.
Таблица 9.8
Предполагаемое
число ремней
Сz
1
2–3
4–5
6–7
1
0,95
0,9
0,85
П р и м е ч а н и е . Более 7 ремней применять не рекомендуется ввиду их
различной длины и неравномерности нагружения.
13. Определить силу F0 предварительного натяжения ремней передачи:
F0 = 750 ∙
P1 C р
V C
+ Z ∙ q ∙ V 2 (Н),
(9.31)
где q – масса 1 метра ремня, кг/м; ее выбирают по табл. 9.9.
114
115.
Таблица 9.9Масса 1 м длины ремня q (кг/м) различных типов ремней
А
0,1
Нормальное сечение
В
С
Д
0,18
0,30
0,62
Е
0,90
Узкое сечение
SPА
SPВ
SPС
0,12
0,20
0,37
14. Определить силу, действующую на валы:
Fr = 2F0 ∙sin 1 Н,
2
(9.32)
где α1 – угол обхвата ремнем малого шкива.
15. Ширину шкивов «В» для клиновых ремней выбирать
из табл. 9.10.
Таблица 9.10
Ширина клиновых шкивов В, мм
Сечение
ремня
А
В
С
1
20
25
34
Ширина В при числе ремней
2
3
4
35
50
65
44
63
82
59
85
101
5
80
101
136
6
95
120
162
16. Проверить прочность клинового ремня.
Максимальное напряжение в сечении ремня, набегающего
на ведущий шкив, определяют по формуле:
mах = 1 + и + V ≤ [ ]р (МПа).
(9.33)
Напряжение в ведущей ветви ремня σ1 складывается из напряжения от предварительного натяжения и полезного напряжения:
1 =
F0
Ft
(МПа),
Z A 2A Z
(9.34)
2 103 T1
где Ft =
– окружная сила на шкиве, Н; Т1 – Н·м; d1 – мм;
d1
Z – число ремней;
А – площадь поперечного сечения определяется по табл. 9.11, мм2.
115
116.
Таблица 9.11Размеры приводных клиновых ремней
Тип ремня
Нормального
сечение
Узкого сечения
Сечение
А
В
С
Д
Е
SPA
SPB
SPC
Площадь
сечения А, мм2
81
138
230
476
692
93
159
278
Высота сечения
ремня h, мм
8
11
14
19
23,5
10
13
18
Напряжение изгиба определяют по формуле:
и = ЕИ
h
(МПа),
d1
(9.35)
где h – высота сечения ремня, мм; ее выбирают по табл. 9.11.
Модуль продольной упругости при изгибе для прорезиненных ремней:
ЕИ = 80–100 МПа.
Напряжение от центробежной силы:
V = ρ ∙V2 ∙ 10-6 (МПа).
(9.36)
Плотность материала клиновых ремней:
ρ = 1100–1250 кг/м3.
Допускаемое напряжение растяжения для клиновых ремней принимают:
[ ]р = 10 МПа.
Если условие max ≤ [ ]р не удовлетворяется, то необходимо или увеличить выбранный в пункте 2 диаметр меньшего
шкива, или принять большее сечение ремня, или увеличить
число ремней и повторить расчет.
116
117.
Глава 10. РАСЧЕТ И ПРОЕКТИРОВАНИЕЦЕПНЫХ ПЕРЕДАЧ
10.1. Общие сведения
Цепная передача относится к передачам зацеплением с
гибкой связью. Она состоит из ведущей (малой), ведомой
(большой) звездочек и цепи (рис. 10.1).
Достоинства цепных передач:
1. По сравнению с зубчатыми цепные передачи могут передавать движение между валами при значительных межосевых
расстояниях (до 5 м).
2. По сравнению с ременными передачами:
а) более компактны;
б) могут передавать большие мощности. Наиболее
часто применяются для мощностей до 120 кВт;
в) значительно меньшая сила предварительного натяжения;
г) постоянство передаточного числа (отсутствует
скольжение и буксование).
3. Могут передавать движение одной цепью нескольким
звездочкам.
Недостатки цепных передач:
1. Значительный шум при работе вследствие удара звена
цепи о зуб звездочки при входе в зацепление. Этот недостаток
ограничивает применение цепных передач при больших скоростях (до 15 м/с).
2. Сравнительно быстрое изнашивание шарниров цепи,
что вызывает необходимость применения системы смазки.
3. Удлинение цепи в силу износа шарниров и сход ее со
звездочек, что требует применения натяжных устройств.
Приводные цепи
Приводная цепь – главный элемент цепной передачи. Она
состоит из соединенных шарнирами отдельных звеньев
(рис. 10.2). Различают роликовые, втулочные и зубчатые привод117
118.
ные цепи. Наиболее широкое распространение имеют роликовыецепи. Основным параметром цепных передач является шаг цепи
Рц. Чем больше шаг, тем выше нагрузочная способность цепи, но
сильный удар звена о зуб в момент набегания на звездочку,
меньше плавность, сильнее шум, больше износ шарниров.
Цепи должны быть прочными и износостойкими. Пластины цепей изготавливают из сталей марок 50, 40Х и др. с закалкой до твердости 40…50 HRC. Оси, втулки, ролики – из цементуемых сталей марок 20, 15Х и др. с закалкой до твердости
52…65 HRC.
Рис. 10.1. Передача цепная:
1 – звездочка малая; 2 – звездочка большая; 3 – цепь
Рис. 10.2. Приводная роликовая цепь
118
119.
10.2. Расчет и проектирование цепных передачс роликовой цепью
Расчет цепных передач с роликовой цепью (рис. 10.1)
удобно вести в следующей последовательности.
1. Определить число зубьев ведущей звездочки Z1. Оно определяется по табл. 10.1 либо путем расчета (формула 10.1).
Таблица 10.1
Число зубьев Z1 ведущей звездочки
Тип цепи
Роликовая
1 2
30–27
Передаточное число
2 3
3 4
4 5
27–25
25–23
23–21
Оптимальное значение Z1: Z1 = 31 – 2U.
5 6
21–17
(10.1)
Минимальное значение Z1min = 29 – 2U.
Полученное значение необходимо округлить до целого
числа. При низких частотах вращения минимальное значение
Z1min = 15 13 зубьев. Для равномерного изнашивания цепи желательно принимать Z1 нечетным числом.
2. Определить число зубьев большой звездочки:
Z2 = Z1 ∙U
(10.2)
(округлить до целого, желательно нечетного, числа).
Максимальное значение числа зубьев большой звездочки:
Z2max = 100...120.
(10.3)
При большем числе зубьев даже у мало изношенной цепи
в результате радиального сползания по профилю зубьев цепь
соскакивает с большой звездочки.
3. Определить фактическое передаточное число:
Z
U′ = 2 .
(10.4)
Z1
U U
Отклонение от заданного: ∆U =
∙100% (допускаемое
U
отклонение ± 3%).
4. Выбрать приводную роликовую однорядную цепь с соответствующим шагом Рц в зависимости от передаваемой мощности
Р (кВт) и частоты вращения малой звездочки п1 (мин-1) по табл. 10.2
(промежуточные значения определяются интерполированием).
119
120.
Таблица 10.2Параметры приводных однорядных роликовых цепей
Приводные роликовые
однорядные цепи типа ПР
(ГОСТ 13568-75)
1
Допускаемые значения передаваемой мощности [Р],
кВт при частоте вращения ведущей
звездочки n1, мин-1 и Z1 = 25 зубьев
50
200
400
600
800
1000
2
3
4
5
6
7
3
0,18
0,62
1,11
1,52
1,87
2,19
8
1
Пр-12,7-10000-1
0,20
0,69
1,24
1,69
2,08
2,43
2
1
Пр-12,7-9000-2
0,19
0,68
1,23
1,68
2,06
2,42
2
1
Пр-12,7-18200-1
0,35
1,27
2,29
3,13
3,86
4,52
2
1
Пр-12,7-18200-2
0,45
1,61
2,91
3,98
4,90
5,74
2
5
Пр-15,875-23000-1
0,57
2,06
3,72
5,08
6,26
7,34
8
5
Пр-15,875-23000-2
0,75
2,70
4,88
6,67
8,22
9,63
8
3
Пр-19,05-31800
1,41
4,80
8,38
11,40
13,50
15,30
4
Пр-25,4-60000 1
3,20
11,0
19,0
25,70
31,0
35,0
1
Пр-31,75-89000 1
5,83
19,30
32,0
42,0
49,0
55,0
4
1
Пр-38,1-127000 1
10,50
35,0
58,0
76,0
89,0
99,0
2
3
Пр-44,45-172400 1
14,70
44,0
71,0
88,0
101
4
П р и м е ч а н и е . В обозначении цепи указан шаг Рц (мм) статическая разрушающая нагрузка Fр (Н) и габарит по ширине (1 или 2).
Пр-9,525-9100
120
121.
По таблице 10.3 определить допускаемое давление [рц] вшарнирах роликов выбранной цепи (при необходимости интерполировать).
Таблица 10.3
Допускаемое давление в шарнирах роликовых цепей [рц], МПа
При частоте вращения ведущей звездочки п1, мин-1
Шаг цепи
Рц, мм
50
200
400
600
800
1000
12,7; 15,875
35
31,5
28,5
26
24
22,5
19,05; 25,4
35
30
26
23,5
21
19
31,75; 38,1
35
29
24
21
18,5
16,5
44,45
35
26
21
17,5
15
–
5. Определить коэффициент эксплуатации:
Кэ = Кд ∙ Ка ∙ Кн ∙ Кс ∙ Крег ∙ Креж ,
(10.5)
где Кд – коэффициент динамической нагрузки, который выбирают в зависимости от условий работы:
− при равномерной нагрузке (например, ленточные или
цепные конвейеры) Кд = 1;
− при неравномерной или толчкообразной нагрузке
(например, скребковый конвейер) Кд = 1,2 – 1,5;
Ка – коэффициент, учитывающий длину цепи (межосевое
расстояние), при а = (30…50)Рц Ка = 1;
Кн – коэффициент, зависящий от угла наклона передачи к
горизонту:
− Кн = 1 при угле наклона передачи к горизонту менее 60 ;
− Кн = 1,25 при угле наклона передачи к горизонту 60 –90 ;
Кс – коэффициент, зависящий от способа смазывания:
− Кс = 0,8 при непрерывном смазывании (например, в
масляной ванне);
− Кс = 1,0 при капельной смазке;
− Кс = 1,3 при периодическом смазывании (замена внутришарнирной консистентной смазки через 120–180 часов работы) и при работе в условиях запыленного производства;
121
122.
Крег – коэффициент, учитывающий способ регулированиянатяжения цепи:
− Крег = 1,0 при регулировании натяжения цепи перемещением оси одной из звездочек;
− Крег = 1,1 при регулировании натяжения цепи оттяжными звездочками или нажимными роликами;
− Крег = 1,15 при периодическом регулировании;
− Крег = 1,25 при отсутствии регулирования натяжения
цепи;
Креж – коэффициент, учитывающий режим работы передачи:
− Креж = 1,0 при односменной работе;
− Креж = 1,25 при двухсменной работе.
6. Определить предварительное значение шага цепи Рц.
Предварительно шаг цепи определяют по формуле:
Рц ≥ 28
3
К э Т1
(мм),
К ряд Z1 р ц
(10.6)
где Кряд – коэффициент числа рядов:
− Кряд = 1 – для однорядных цепей;
− Кряд = 1,75 – для двухрядных цепей.
После этого производят окончательный выбор цепи по
мощности Р (кВт) и допускаемому давлению [р]ц.
7. Определить делительные диаметры ведущей и ведомой
звездочек:
Рц
d1 =
(мм);
(10.7)
180
sin
Z1
d2 =
Рц
sin
180
Z2
(мм).
(10.8)
8. Определить диаметры выступов ведущей и ведомой
звездочек:
180
De1 = Рц ∙ (ctg
+ 0,5) мм;
(10.9)
Z1
122
123.
De2 = Рц · (ctg180
+ 0,5) мм.
Z2
(10.10)
9. Определить диаметры окружности впадин ведущей и
ведомой звездочек:
Di1 = d1 – dp (мм);
(10.11)
Di2 = d2 – dp (мм),
(10.12)
где dp – диаметр ролика цепи (выбирают по табл. 10.4).
Таблица 10.4
Размеры и параметры приводных роликовых однорядных цепей
Обозначение цепи
ПР-9,525-9100
ПР-12,7-10000-1
ПР-12,7-9000-2
ПР-12,7-18200-1
ПР-12,7-18200-2
ПР-15,875-23000-1
ПР-15,875-23000-2
ПР-19,05-31800
ПР-25,4-60000
ПР-31,75-89000
ПР-38,1-127000
ПР-44,45-172400
Шаг
цепи
Рц, мм
Диаметр
ролика
dp, мм
9,525
12,7
12,7
12,7
12,7
15,875
15,875
19,05
25,4
31,75
38,1
44,45
6,36
7,75
7,75
8,51
8,51
10,16
10,16
11,91
15,88
19,05
22,23
25,40
Диаметр
оси
ролика
d, мм
3,28
3,66
3,66
4,45
4,45
5,08
5,08
5,94
7,92
9,53
11,10
12,70
Длина
втулки
цепи
Ввн, мм
5,72
5,80
5,80
8,90
11,30
10,11
13,28
17,75
22,61
27,46
35,46
37,19
Масса
1 м цепи
q, кг/м
0,45
0,30
0,35
0,65
0,75
0,80
1,0
1,9
2,6
3,8
5,5
7,5
10. Определить окружную силу, передаваемую цепью:
T1 2 103
Ft =
(Н).
d1
(10.13)
11. Определить давление в шарнирах цепи рц и сравнить с
допускаемыми значениями:
F K
рц = t э ≤ [р]ц,
(10.14)
d Ввн
где диаметр оси роликовой цепи d и длину втулки Ввн выбирают
по табл. 10.4.
123
124.
Если условие рц ≤ [р]ц не удовлетворяется, то необходимоповторить расчет, либо увеличив число зубьев ведущей звездочки Z1, либо выбрав цепь с большим шагом Рц, либо увеличив
число рядов цепи.
12. Определить предварительное значение межосевого
расстояния:
а′ = (30 50)Рц (мм).
(10.15)
13. Определить длину цепи, выраженную в шагах или числом звеньев цепи:
2
Z 2 Z1 Z 2 Z1 Рц
2
a
Lp′ =
(10.16)
.
Рц
2
2
a
Полученное значение необходимо округлить до целого
четного числа Lp.
14. Определить уточненное значение межосевого расстояния:
Рц
Z 2 Z1
Z 2 Z1 2 Z 2 Z1 2
а=
мм. (10.17)
8
L
L р
2
4 p
2
2
Для свободного провисания цепи рекомендуется уменьшить межосевое расстояние на 0,003а и принять окончательное
значение а (мм), округлив его до целого числа.
15. Определить натяжение от силы тяжести свободной
ветви цепи:
F0 = K f ∙ a ∙ q ∙ g ,
(10.18)
где Kf – коэффициент провисания, зависящий от расположения
передачи:
− Kf = 1 при вертикальном расположении передачи;
− Kf = 3 при угле наклона передачи меньше 45 ;
− Kf = 6 при горизонтальном расположении передачи;
q (кг/м) – погонная масса 1 метра цепи. Выбирают по
табл. 10.4.
g = 9,81 м/с2.
124
125.
16. Определить нагрузку на валы*:Fв = Кв ∙ Ft + 2F0 (H),
(10.19)
где Кв – коэффициент нагрузки вала:
− Кв = 1,15 при угле наклона передачи меньше 45 ;
− Кв = 1,05 при угле наклона передачи 45 –90 .
17. Определить коэффициент запаса прочности цепи S и
сравнить его с допускаемым [S] (должно быть S ≥ [S]).
Fp
S=
≥ [S],
(10.20)
Ft K д FV F0
где Fp – статическая разрушающая нагрузка (указывается в обозначении цепи – табл. 10.2 и 10.4);
FV = qV2 (Н) – натяжение цепи от центробежных сил;
Скорость движения цепи:
Рц Z1 n1
V=
(м/с).
(10.21)
60 1000
Значения допускаемого коэффициента запаса [S] приведены
в табл. 10.5.
Таблица 10.5
Допускаемый коэффициент запаса прочности [S] для роликовых
цепей при Z1 = 15 30
Шаг Рц, мм
12,7
15,875
19,05
25,4
31,75
38,1
44,4
*
Частота вращения ведущей звездочки п1, мин-1
50
7,1
7,2
7,2
7,3
7,4
7,5
7,6
100
7,3
7,4
7,8
7,8
7,8
8
8,1
200
7,6
7,8
8
8,3
8,6
8,9
9,2
300
7,9
8,2
8,4
8,9
9,4
9,8
10,3
400
8,2
8,6
8,9
9,5
10,2
10,8
11,4
500
8,5
8,9
9,4
10,2
11
11,8
12,5
600
8,8
9,3
9,7
10,8
11,8
12,7
–
800
9,4
10,1
10,8
12
13,4
–
–
Нагрузку на валы можно определить также и по приближенной формуле Fв
125
1000
10
10,8
11,7
13,3
–
–
–
1,15 Ft (H)
126.
ЧАСТЬ IV. СОЕДИНЕНИЯПо признаку разъемности все виды соединений можно
разделить на разъемные и неразъемные.
Разъемные – шпоночные и шлицевые, резьбовые, штифтовые, клеммовые, профильные.
Неразъемные – сварные, заклепочные, соединения с натягом, клеевые.
Глава 11. ШПОНОЧНЫЕ И ШЛИЦЕВЫЕ СОЕДИНЕНИЯ
11.1. Шпоночные соединения и их расчет
Шпонки служат для передачи вращающего момента с вала
на ступицу или наоборот (рис. 11.1).
Рис. 11.1. Схема шпоночного соединения
Ступицы имеют зубчатые колеса, шкивы, звездочки, полумуфты и др.
Пазы на валах под шпонки выполняются фрезерованием
(дисковой или концевой фрезой), а пазы в ступицах – либо
долблением, либо протягиванием.
Различают три основных вида шпоночных соединений:
− призматическими шпонками;
− клиновыми шпонками;
− сегментными шпонками.
126
127.
Призматические шпонкиПризматические шпонки (рис. 11.2) выполняют прямоугольного сечения, причем их концы выполняют плоскими или
скругленными, а боковые грани являются рабочими. Шпонки
изготавливают из среднеуглеродистой стали. Их врезают в вал
на глубину около 0,6 от ее высоты, т.е. t1 ≈ 0,6h. В радиальном
направлении предусматривается зазор.
Рис. 11.2. Соединение призматическими шпонками:
а) шпонка со скругленными концами;
б) шпонка с плоскими концами
Призматические шпонки по назначению разделяют на:
− простые, предназначенные только для передачи вращающего момента;
− направляющие и скользящие, допускающие осевое перемещение (например, в коробке передач).
Размеры шпонок стандартизованы. Ширину шпонки В
обычно выбирают:
В = (0,25…0,30)d (мм).
(11.1)
Основным расчетом для призматических шпонок является
расчет на смятие боковых граней. Условие прочности на смятие:
F
(11.2)
см = t ≤ [ ]см (МПа),
A
где Ft = 2T (Н), а площадь смятия А = t1 ∙ lp (мм2);
d
lp – рабочая длина шпонки.
127
128.
2T ≤ [ ] (МПа).(11.3)
см
d t1 l p
Из этой формулы можно найти необходимую рабочую
длину шпонки:
2T
lp =
(мм),
(11.4)
см d t1
а для шпонки со скругленными краями и полную ее длину –
l = lp + В (мм).
Допускаемые напряжения смятия для шпонки, изготовленной из стали 45:
для простых шпонок – [ ]см = 100…120 МПа;
для направляющих шпонок – [ ]см = 20…30 МПа.
Тогда см =
Клиновые шпонки
В отличие от призматических, у клиновых шпонок
(рис. 11.3) рабочими являются широкие грани, а по боковым
граням имеется зазор. Их используют в тихоходных передачах,
так как они дают более грубое соединение, чем призматические
шпонки, но дешевле.
Рис. 11.3. Соединение клиновой шпонкой
Недостатки клиновых шпонок:
128
129.
− требуется предварительная затяжка шпонок;− создают напряженное соединение;
− имеет место радиальное смещение оси ступицы по отношению к оси вала.
Сегментные шпонки
Глубокая посадка сегментной шпонки (рис. 11.4) обеспечивает ей более устойчивое положение, чем у призматической
шпонки, однако, глубокий паз значительно ослабляет вал, поэтому сегментные шпонки применяют главным образом для закрепления деталей на малонагруженных участках валов. Эти
шпонки стандартизированы в зависимости от диаметра вала.
Рис. 11.4. Соединение сегментной шпонкой
11.2. Шлицевые соединения и их расчет
Шлицевые соединения вал–ступица (рис. 11.5) представляют собой соединения, образуемые выступами – зубьями на
валу, входящими во впадины соответствующей формы в ступице. Эти соединения можно представить как многошпоночные, у
которых шпонки и вал выполнены как единое целое.
129
130.
Dd
Рис. 11.5. Основные типы зубчатых соединений
а) прямобочное; б) эвольвентное; в) треугольное
Преимущества шлицевых соединений по сравнению со
шпоночными:
− большая несущая способность;
− большая усталостная прочность вала;
− лучшая центровка и лучшее направление при передвижении вдоль оси вала.
Наибольшее применение (до 90%) имеют прямобочные
шлицевые соединения с числом зубьев в зависимости от диаметра:
− легкой серии при d = 26…120 мм
Z = 6, 8, 10;
− средней серии при d = 14…125 мм
Z = 6, 8, 10;
− тяжелой серии при d = 20…125 мм
Z = 10, 16, 20.
Прямобочные шлицевые соединения могут иметь три способа центрирования:
− по боковым граням;
− по наружному диаметру;
− по внутреннему диаметру.
Эвольвентные шлицевые соединения характеризуются
уменьшенной высотой зуба (0,9…1,0)т и профильным углом
α = 30°. Они имеют достоинства: повышенную прочность и
технологичность.
Число зубьев у эвольвентных шлицевых соединений
Z = 11…50; модули т = 1; 1,5; 2; 2,5;…10 мм. Центрирование
осуществляется по боковым поверхностям, реже по наружному
диаметру.
130
131.
Шлицевые соединения треугольного профиля, как правило, неподвижные, с числом зубьев Z = 20…70. Центрированиетолько по боковым граням.
Шлицевые соединения, так же как и шпоночные, рассчитывают на смятие:
2T
≤ [ ]см (МПа),
(11.5)
см =
h l ψ z d cp
D d
– высота поверхности контакта;
2
l – длина поверхности контакта;
= 0,75 – коэффициент неравномерности работы зубьев;
Z– число зубьев;
D d
dcp =
;
2
[ ]см принимают таким же, как и у шпоночных соединений.
где h=
Глава 12. РЕЗЬБОВЫЕ СОЕДИНЕНИЯ
Соединения деталей с помощью резьбы является одним из
старейших и наиболее распространенных видов разъемных соединений.
12.1. Резьбы. Общие сведения
По форме основной поверхности различают цилиндрические и конические резьбы. Наиболее распространены цилиндрические. Коническую резьбу применяют для плотных соединений труб, масленок, пробок.
Профиль резьбы может быть треугольный, прямоугольный, трапецеидальный, круглый и др.
По направлению винтовой линии различают правую и левую резьбу.
У правой резьбы винтовая линия идет слева вверх направо
(рис. 12.1), у левой – справа вверх налево.
131
132.
Рис. 12.1. Схема образования винтовой линии у правой резьбыЛевую применяют в специальных случаях.
По числу заходов резьба бывает одно- и многозаходная
(рис. 12.2). Все крепежные резьбы однозаходные. Многозаходные применяют в винтовых механизмах.
Рис. 12.2. К определению числа заходов резьбы
Методы изготовления
1. Нарезка вручную метчиками или плашками.
2. Нарезка на токарно-винторезных или специальных
станках.
132
133.
3. Фрезерование на специальных резьбофрезерных станках (больше диаметры) – ходовые и грузовые винты, резьбы навалах и т.д.
4. Накатка на специальных резьбонакатных станкахавтоматах. Способ высокопроизводителен и дешев. Упрочняет
резьбовые детали.
5. Литье на деталях из стекла, пластмассы, металлокерамики и т.д.
6. Выдавливание на тонкостенных давленных и штампованных изделиях из жести, пластмассы и т.д.
Геометрические параметры резьбы
Рис. 12.3. Геометрические параметры метрической резьбы:
d1 – внутренний диаметр; d2 – средний диаметр;
d – наружный диаметр; Р – шаг
(d и d1 – одинаковые для винта и гайки);
h – рабочая высота профиля; Рh – ход, для однозаходной
Рh = Р; для многозаходной Рh = nP, где n – число заходов;
– угол профиля; – угол подъема винтовой линии
Основные типы резьб:
1. Крепежные – метрическая, трубная – треугольные со
скругленными вершинами и впадинами, круглая.
2. Ходовые резьбы – прямоугольная, трапецеидальная, симметричная и несимметричная (упорная = 3о).
133
134.
Резьба метрическая получила свое название из-за того, чтовсе ее размеры измеряются в миллиметрах. Вершины витков и
впадин притуплены по прямой или по дуге окружности для
уменьшения концентрации напряжений, предохранения от забоев
в эксплуатации и для повышения стойкости инструмента при нарезании. Метрические резьбы бывают с крупным и мелким шагом.
Например, для диаметра 14 мм стандарт предусматривает
крупный шаг 2 мм и 5 мелких резьб с шагом 1,5; 1,25; 1,0; 0,75
и 0,5 мм. При уменьшении шага уменьшается высота резьбы и
угол подъема резьбы увеличивается прочность стержня винта и
увеличивает самоторможение.
Резьба трубная применяется для
герметичного соединения труб и
арматуры. На тонкой стенке трубы
нельзя нарезать резьбу с крупным
шагом без уменьшения прочности
трубы, поэтому трубная резьба имеет
мелкий шаг.
В международном стандарте для трубной резьбы сохранено измерение в дюймах. Для лучшего уплотнения трубную резьбу
выполняют без зазоров по выступам и впадинам и с закруглениями профиля. Высокую плотность соединения дает коническая трубная резьба (за счет плотного прилегания профилей по
вершинам при затяжке), но она сложнее в изготовлении, чем
цилиндрическая.
Резьба круглая удобна
для
изготовления
литьем пластмассовых,
чугунных, стеклянных,
а также накаткой и
выдавливанием
на
тонкостенных
металлических
и
пластмассовых деталях.
134
135.
Резьба прямоугольнаяшироко применялась в
винтовых механизмах,
не стандартизирована и
почти
вытеснена
трапецеидальной.
Резьбу
трапецеидальную
с
симметричным
профилем применяют
для
реверсивных
движений
под
нагрузкой.
С
несимметричным
профилем применяют
для одностороннего
движения
под
нагрузкой.
Она
называется упорной
резьбой.
Способы стопорения: а) контргайка, пружинная шайба,
натяг в резьбе;
135
136.
б) гайку жестко соединяют со стержнем при помощишплинтов, проволоки, многолапчатой шайбы и др.
Нормальная высота крепежных гаек Н = 0,8d; высокие
гайки Н 1,2; низкие Н 0,5d.
Глубина завинчивания в стальные детали Н (1…1,25)d; в
чугунные и силуминовые Н (1,25…1,5)d.
12.2. Обозначение болтовых соединений
В порядке понижения точности изготовления различают
болты классов точности А, В, С. Болты с шестигранной головкой класса точности А изготавливают по ГОСТ 7805-70, с шестигранной головкой класса точности В – по ГОСТ 7798-70, болты с шестигранной уменьшенной головкой класса точности В –
по ГОСТ 7796-70.
Болт диаметром резьбы 12 мм, длиной 60 мм, класса
прочности 5.8, с крупным шагом резьбы, без покрытия, с полем
допуска 6д:
Болт М12 – 6д 60.5.8. ГОСТ 7798-70.
То же из легированной стали 35Х, класса прочности 8.8,
с мелким шагом резьбы:
Болт М12 1,25 – 6д 60.8.8 35Х ГОСТ 7798-70.
Для стандартных болтов установлены 12 классов прочности, которые обозначаются двумя числами, между которыми
ставят точку. Первое число, умноженное на 100, определяет
минимальное значение в (МПа); произведение этих двух чисел,
умноженное на 10, дает минимальную величину предела текучести т (МПа).
Для стандартных шестигранных гаек с высотой Н = 0,8d
ГОСТ 5915-70 установлены 7 классов прочности, обозначаемых
одним числом, например 4, 5, 6, 8 … 12. Это число указывает
наибольший класс прочности болта, с которым гайка может
быть сопряжена в соединении. Например, гайка класса прочности 6 может быть применена в соединении с болтом класса
прочности не выше 6.8.
136
137.
Гайка диаметром резьбы d = 12 мм, с крупным шагомрезьбы, с полем допуска 6Н, класса прочности 5, без покрытия:
Гайка М12–6Н.5 ГОСТ 5915-70.
12.3. Расчет незатянутых винтов
Как правило, на практике приходится иметь дело с затянутыми винтами. Незатянутые встречаются довольно редко.
Незатянутые винты – это винты, на которые вначале навинчена гайка и лишь затем приложена рабочая нагрузка.
Пример – стержень крюка (скобы), (рис. 12.4).
Рис. 12.4. Резьбовые соединения без предварительной затяжки
На рисунке 12.5 показано распределение нагрузки между
витками резьбы такого соединения.
137
138.
Рис. 12.5. Характер распределения нагрузки между витками резьбы(решение Н.Е. Жуковского)
При равномерном распреде- При
равномерном
лении нагрузки по виткам распределении нагрузки (по
резьбы
Жуковскому)
В гайке с 10 витками каждый
Если в гайке Z = H витков, виток передает не 0,1F, а слеP
дующую нагрузку:
то каждый виток передает 1й – 34F;
2й – 0,23F;
часть силы: F .
Z
3й – 0,15F;
……………….
10й – < 0,01F.
На рисунке 12.6 представлены гайки с более равномерным
распределением нагрузки по виткам резьбы. При приложении
нагрузки шаг резьбы на стержне винта увеличивается, а на гайке уменьшается.
138
139.
Рис. 12.6. Гайки с более равномерным распределением нагрузки:а) висячая гайка; б) с кольцевой выточкой
Расчетные уравнения для стержня болта (на растяжение)
Для проверочного расчета (рис. 12.7):
F F2 p (МПа)
A d1
(12.2)
4
или
d12
F p A p
(Н)
4
Рис. 12.7. Схема нагружения стержня болта
139
(12.3)
140.
Для проектного расчета:d1
4F
(мм).
p
(12.4)
Полученное значение d1 округляется до ближайшего
большего стандартного значения, по которому определяется
диаметр d.
12.4. Материалы для изготовления деталей резьбовых
соединений и допускаемые напряжения
В качестве материалов для изготовления резьбовых деталей применяются углеродистые и легированные стали – Ст3,
Ст10, Ст20, Ст35, Ст40, Ст45, Ст35Х, Ст30 ХГСА и др. Стандартные крепежные изделия изготавливаются из низко- и среднеуглеродистых сталей, а ответственные и высоконагруженные
детали – из легированных сталей.
Допускаемые напряжения на растяжение для болтов:
p т
(МПа),
(12.5)
S
где т – предел текучести материала;
S – коэффициент безопасности.
Можно задаваться: S = 1,5 2,5 для болтов из углеродистых
сталей;
S = 3 4 для болтов из легированных
сталей.
При малых диаметрах болтов, например менее 16 мм из
углеродистой стали и менее 8 мм из легированной стали, применяют даже S = 4 6, опасаясь перетяжки болтов при затяжке.
От перетяжки болты и шпильки предохраняют предельные
или динамометрические ключи.
140
141.
В особо ответственных случаях (например авиационныеболты) затяжка контролируется по удлинению стержня (микрометром или индикатором).
Допускаемые напряжения на смятие для болтов, установленных под «развертку»:
см (0,3 0,4) т (МПа).
(12.6)
Допускаемые напряжения на срез для болтов, установленных под «развертку»:
ср (0,2 0,3) т (МПа).
12.5. Расчет резьбы на прочность
Рис. 12.8. К расчету резьбы на прочность
141
(12.7)
142.
В отличие от стержня, работающего на разрыв, резьба испытывает во время работы (под нагрузкой) (рис. 12.8):а) срез по цилиндрическим поверхностям аb (на стержне)
и сe (в гайке) в пределах высоты Н;
б) смятие по кольцевым площадкам bc и de.
Расчет на срез
Этот расчет проверочный, так как все размеры резьб заданы стандартом.
На стержне болта:
В гайке:
F
F
ср (МПа).
A d1 H K
F
F
ср (МПа).
ср
A d H K
ср
(12.8)
(12.9)
Следовательно, при одинаковых материалах среза болта и
гайки резьба обычно срезается на стержне болта (т.к. площадь
среза меньше). При разных материалах проверку ведут по обоим уравнениям.
Допускаемое напряжение среза – формула (12.7).
Коэффициент К в формулах (12.8) и (12.9) учитывает неполноту площади среза (рис. 12.9).
K P 1
P
Рис. 12.9. К определению коэффициента неполноты резьбы
142
143.
По стандартам резьб К = 7 0,87 – у метрических резьб8
К = 5 0,83 – у дюймовых резьб
6
К = 3 0,75 – у упорных резьб
4
К = 2 0,67 – у трапецеидальных резьб
3
К = 1 0,5 – у квадратных резьб
2
Расчет на смятие
Площадь проекции поверхности витка на плоскость, пер2 d 2
d
пендикулярную к силе F: A
1 .
4
4
Расчетное уравнение:
см F
A Z
F P
см (МПа),
2
d 2 d1 H
4
4
(12.10)
так как число рабочих витков в гайке Z = Н .
Р
Допускаемое напряжение смятия в резьбе – формула (12.6).
П р и м е ч а н и е. При расчетах резьб предполагается равномерное распределение нагрузки F по виткам гайки. Исходя из
этого, выбираются и рекомендованные выше допускаемые напряжения на срез и смятие.
143
144.
12.6. Усилия и моменты, действующие в резьбовыхсоединениях при затяжке
Рис. 12.10. Схема к определению сил и моментов
в резьбовом соединении при завинчивании и отвинчивании
Из треугольника сил (рис. 12.10) определяется сила Ft:
Ft = F tg( + ),
(12.11)
где – угол наклона винтовой линии;
– угол трения, равный arctg f (для крепежных резьб
f = 0,15).
Момент в резьбе Тр от приложенной силы Ft на среднем
диаметре d2 определяется следующим образом:
T p Ft
d2
0,5 tg(ψ ) d 2 .
2
(12.12)
Формула 12.14 справедлива для квадратной резьбы. Окружная сила трения в треугольной резьбе больше. Соотношение
сил трения в прямоугольной и треугольной резьбах рассмотрим
на рис. 12.11.
144
145.
Рис. 12.11. Схема для определения соотношений силв треугольной резьбе
Тогда
Fтр F f ;
Fтр Fn f
F
cos
2
F f1 ,
(12.13)
где – угол профиля резьбы;
f
f1 =
– приведенный коэффициент трения в резьбе; (12.14)
cos
2
о
= 60 – для метрической резьбы;
= 55о – для дюймовой резьбы;
= 30о – для трапецеидальной резьбы;
= 0о – для квадратной резьбы.
Следовательно, наибольшие потери на трение будут в
метрической и дюймовой резьбах, а наименьшие – в квадратной. Для крепежной метрической резьбы это важно, так как
способствует самоторможению резьбы.
Аналогичное соотношение имеет место между углами
трения:
1
.
(12.15)
cos
2
Тогда формулы для определения окружной силы Ft и момента в резьбе Тр для остроугольных резьб примут вид:
Ft = F tg( + 1);
Тр = 0,5 F tg( + ).
145
(12.16)
(12.17)
146.
Момент Тр в резьбе скручивает стержень витка.Рис. 12.12. Схема к определению зависимости между моментом,
приложенным к гайке, и осевой силой
На опорной кольцевой поверхности под гайкой (рис. 12.12)
возникает сила трения Fтр = F f. Приближенно можно считать,
что эта сила приложена по среднему диаметру кольцевой опорной
поверхности:
D d0
d ср
,
(12.18)
2
где D – наружный диаметр этого кольца, равный размеру под
ключ;
d0 – внутренний диаметр кольца, т.е. отверстие под винт d0.
Тогда момент сил трения на торце гайки Tт :
Tт F f
d ср
2
F f
d ср
2
.
Окончательно получаем:
d ср
Т зав F 0,5d 2 tg ψ 1 f
.
2
(12.19)
(12.20)
П р и м е ч а н и е. Для метрической резьбы с крупным шагом можно приближенно принять: 2о 30 ; d2 0,9d; D 1,35d;
146
147.
d0 = 1,1d; f = 0,15. После подстановки числовых значений в уравнение (12.20) получаем:Tзав 0,2 F d .
(12.21)
При стандартной длине гаечного ключа Lкл, равной 14d, из
условия Tзав F раб Lкл получаем:
F 30F раб ,
(12.22)
где F раб – сила, приложенная рабочим на конце ключа.
При отвинчивании элемент гайки движется вниз и сила
трения в резьбе Fтр Fn f меняет направление. Тогда момент,
необходимый для отвинчивания гайки, получают аналогично
моменту завинчивания, только знак угла подъема меняют на
обратный:
d ср
Т отв F 0,5d 2 tg 1 ψ f
(12.23)
.
2
При отсутствии трения на торце гайки второй член уравнения равен 0.
Тогда условие самоторможения Tотв 0, отсюда для резьбы без трения на торце гайки tg ( 1 ) 0 и, следовательно,
< 1. Для нормальных метрических резьб с углом подъема
около 2о30 самоторможение наступает при 1 2о30 , т.е.
при f 0,045, а приведенный угол трения изменяется в пределах
от 6о (при f 0,1) до 16о (при f 0,3).
Таким образом, все крепежные резьбы при действии статической нагрузки являются самотормозящими. Однако в условиях вибрационных нагрузок возможно ослабление затяжки
резьбы, во избежание которого применяют специальные стопорные устройства.
КПД резьбы и резьбового соединения
КПД резьбы определяется как отношение полезной работы
на винте к затрачиваемой работе на ключе:
147
148.
tgψ.
(12.24)
tg (ψ 1 )
При = 2о30 и f = 0,1 η 0,3.
КПД резьбового соединения (винт + гайка + торец):
tgψ
η
.
(12.25)
d ср
tg(ψ 1 ) f
2
η
Расчет затянутых болтов и винтов
Это винтовые соединения, к которым нагрузка прикладывается в процессе затягивания гайки. Стержень таких винтов
нагружен силой растяжения Fзат и скручивающим моментом от
сил трения в резьбе Тр. Таким образом, в стержне возникают
нормальные и касательные напряжения.
Эквивалентное напряжение определяется по энергетической теории прочности:
экв 2p 3 2 p .
(12.26)
Нормальное напряжение растяжения определяется по
формуле:
F
р зат (МПа),
(12.27)
A
d12
где A
– площадь опасного сечения резьбы по расчетному
4
диаметру резьбы, мм2.
Касательное напряжение:
Т р 0,5Fзат d 2 tg (ψ 1 )
,
(12.28)
τ
3
Wкр
d1
16
где Тр – момент в резьбе (Н м);
Wкр – момент сопротивления при кручении (мм3).
Для стандартных метрических резьб можно принять
экв 1,3 , что позволяет рассчитывать болты по упрощенному
выражению:
148
149.
экв 1,34Fзат
d12
p (МПа),
(12.29)
т
– допускаемые напряжения растяжения, МПа.
S
Физический смысл коэффициента 1,3 заключается в том,
что с его помощью учитывают действие в стержне касательных
напряжений от момента сопротивления в резьбе.
При проектном расчете диаметр d1 можно определить из
формулы (12.29):
1,3 4 Fзат
d1
(мм)
(12.30)
р
и по нему подобрать резьбу из стандартного ряда.
где p
12.7. Основные случаи расчета резьбовых соединений
Расчет болтов, нагруженных поперечными силами
1. Болты чистые, поставлены в отверстие без зазора («под
развертку»), рис. 12.13.
Эти болты работают на срез и на смятие.
Рис. 12.13. Схема к расчету чистых болтов, нагруженных
поперечными силами
149
150.
Напряжение среза:F
ср (МПа),
(12.31)
d 02
Z
4
где ср = (0,2 0,3) т – допускаемое напряжение на срез при
статической нагрузке;
Z – число болтов.
Напряжение смятия:
см F см (МПа),
(12.32)
d0 Z
где d 0 – проекция боковой поверхности смятия на плоскость, перпендикулярную силе F;
см = (0,3 0,4) т – для стальных деталей (см. 12.6).
По формуле 12.32 определяется d0:
F
d0
(мм)
(12.33)
см Z
и по нему подбирается болт из стандартного ряда.
ср
2. Болты обыкновенные, подставлены в отверстие с зазором (рис. 12.14).
Эти болты работают на растяжение и скручивание.
Рис. 12.14. Схема к расчету обыкновенных болтов, нагруженных
поперечными силами
150
151.
В этом случае соединение удерживается от сдвига силойтрения от затяжки болтов. Необходимое условие:
(12.34)
F Fтр или KF Fзат f Z i ,
где f = 0,15 0,20 – коэффициент трения для сухих поверхностей;
Z – число болтов;
i – число стыков (на рис. 12.14 i = 2);
К – коэффициент запаса; К = 1,3 1,5 при статической нагрузке; К = 1,8 2 при переменной нагрузке.
Из формулы 12.34 определяется величина силы затяжки
болта Fзат, а по формуле 12.31 – расчетный диаметр болта d1, по
которому подбирается болт из стандартного ряда.
Fзат KF .
(12.35)
f Z i
Расчет группы болтов, нагруженных силой и моментом
в плоскости стыка соединяемых деталей (рис. 12.15)
Дано: внешняя сила F, угол , под которым действует сила F, геометрические размеры.
Рис. 12.15. Соединение, нагруженное силой и моментом в плоскости
стыка (а), и его расчетная схема (б)
151
152.
В расчете приняты следующие допущения:− все болты одного диаметра и затянуты с одинаковой
силой;
− поверхности стыка не деформируются;
− поверхности стыка имеют оси симметрии;
− силы, действующие от внешнего момента на болты,
прямо пропорциональны расстояниям от них до т. О.
Разлагаем силу F внешней нагрузки на кронштейн на две
взаимно перпендикулярные силы F1 и F2. Переносим силы F1 и
F2 в центр тяжести О с добавлением момента Т = F1 l. Сила F1
сдвигает соединение по оси Y, сила F2 – по оси Х, а момент
стремится повернуть кронштейн вокруг т. О. Направление реакций болтов перпендикулярно радиусам r1 и r2.
Из условия равновесия соединения можно записать*:
M 0 0; 4 FT 1 r1 2 FT 2 r2 T .
(12.36)
Из условия, что силы пропорциональны плечам, можно
записать:
FT 1 FT 2
.
r1
r2
(12.37)
Рис. 12.16. Схема к определению зависимости сил F от расстояний
до них от точки D
*
Примечание: обозначим силы от момента Т, приходящиеся на болты в т. 1, 2, 3,
4, 5, – F1Т =F2Т =F4Т =F5Т =F1Т, а силы, приходящиеся на болты в т. 3, 6, – F3Т =F6Т =F2Т.
152
153.
Решая совместно систему уравнений 12.36 и 12.37, определяют силы FT1 и FT2:F r
F r
FT 2 T 1 2 4 FT 1 r1 2 T 1 2 r2 T .
(12.38)
r1
r1
Отсюда сила от момента, приходящаяся на наиболее нагруженные болты, расположенные на расстоянии r1 от т. О:
Т r
FT 1 2 1 2 .
(12.39)
4r1 2r2
Центрально приложенные силы F1 и F2 распределяются
равномерно по болтам:
F F
F
F
Fy 1 1 ; Fх 2 2 ; F Fх2 Fy2 .
(12.40)
Z
6
Z
6
Суммарная нагрузка, приходящаяся на каждый болт, равна
геометрической сумме сил F и FТ. В рассматриваемом случае
наиболее нагруженным оказался нижний правый болт. Остальные болты нагружены меньше.
Здесь также возможны два случая:
– болты поставлены без зазора;
– болты поставлены с зазором.
Когда болты поставлены без зазора, нагрузка воспринимается непосредственно болтами, работающими на срез и на смятие. Расчет ведется по формулам (12.31) и (12.32).
Когда болты поставлены с зазором, нагрузка воспринимается силами трения на стыке деталей в результате затяжки болта.
Условие отсутствия сдвига:
(12.41)
Fтр F .
Потребная сила затяжки:
S F
Fзат сд ,
(12.42)
f
где F – расчетная сдвигающая сила, приходящаяся на один болт
(в рассматриваемом случае это болт 5);
f – коэффициент трения, принимаемый f = 0,15 0,2;
S сд – коэффициент запаса сцепления по сдвигу, S = 1,2 2.
Прочность болтов рассчитывается по формуле 12.29.
153
154.
Расчет группы болтов, нагруженных силамии моментами, действующими в плоскости,
перпендикулярной плоскости стыка
Это, например, болты крепления электродвигателей станков и редукторов к раме или плитам, а последних – к фундаменту. Это болты крепления кронштейнов и подвесок к колоннам,
стенам и потолку зданий и т.д.
Стыки деталей, стягиваемых болтами, могут быть металлическими (редуктор на плите) и неметаллическими (плита на
фундаменте).
На рисунке 12.17 показана схема нагружения кронштейна,
стоящего на бетонном основании. Даны размеры кронштейна и
внешняя сила F. Кронштейн закреплен четырьмя болтами и нагружен внешней силой F, направленной по углом к горизонту. Кронштейн симметричный, центр масс расположен на пересечении осей Х и Y в точке, обозначенной т.О. Разложим силу F
на вертикальную отрывающую силу Fот F sin и горизонтальную сдвигающую силу Fсд F cos . Переносим силы Fот и
Fсд в т.О с добавлением момента Т = Fсд Н. Таким образом,
кронштейн нагружен отрывающей силой Fот, сдвигающей силой Fсд и опрокидывающим моментом Т. Под действием отрывающей силы и опрокидывающего момента в левой части стыка
может произойти его раскрытие, что недопустимо. Таким образом, сила затяжки болтов должна обеспечивать нераскрытие
стыка и отсутствие сдвига.
Определение силы затяжки болтов из условия
нераскрытия стыка
На рисунке 12.17 показаны эпюры напряжений от действующих сил:
– от силы затяжки (предполагается, что силы распределены равномерно по площади стыка)
F Z
0 зат ,
(12.43)
Aст
где Z = 4 – число болтов крепления кронштейна к основанию;
Аст = а(L – l) – площадь стыка (мм2);
154
155.
Рис. 12.17. К расчету группы болтов, нагруженных силамии моментами, действующими в плоскости, перпендикулярной
плоскости стыка
155
156.
– от внешней силы Fотот
Fот (1 )
,
Аст
где – коэффициент основной нагрузки;
д
,
б д
где д и б – податливость детали и болта.
(12.44)
(12.45)
Этот коэффициент показывает, какая доля от внешней силы Fот идет на увеличение нагрузки на болт F и какая часть
идет на разгрузку стыка (1 – )F;
– от момента Т
Т (1 )
мом
,
(12.46)
Wст
где Т = Fсд Н;
a L3 al 3
2
12
12
Wст
– момент сопротивления стыка (мм3).
L
Для выполнения условия нераскрытия стыка должно быть:
min 0 от мом 0 .
(12.47)
Необходимое напряжение предварительной затяжки определяется следующим образом:
0 min от мом ,
(12.48)
а сила болтов
0 Аст
.
(12.49)
Z
Затем необходимо проверить прочность основания (бетона) в точке В – точке действия максимальных напряжений сжатия:
max см ,
(12.50)
Fзат
где max 0 от мом и см = 1…2 МПа для бетона.
156
157.
Определение силы затяжки болтов из условия отсутствия сдвига деталей в стыке (выполняется как проверочный)Условие отсутствия сдвига:
(12.51)
Fтр К Fсд ,
где К = 1,5 2 – коэффициент запаса по сдвигу.
Fтр Fn f ,
где Fn – нормальная сила в поверхности контакта.
(12.52)
В рассматриваемом случае:
Fn Z Fзат Fот (1 ) .
(12.53)
Подставляя в формулу 12.52, получаем:
ZF
Fот (1 ) f KFсд ,
зат
(12.54)
отсюда
Fзат
KF
сд
f
Fот (1 )
.
Z
После расчета необходимой силы затяжки по этим двум
критериям принимают большую Fзат и по ней определяют силу, действующую на болт:
Fб 1,3Fзат Fдоп ,
F
где Fдоп от T – дополнительная нагрузка на болт от отрыr
Z
вающей силы Fот и опрокидывающего момента Т.
Здесь r – расстояние от оси Y до оси болта, наиболее удаленного от центра масс.
Расчетный диаметр болта:
4Fб
dp
(мм).
p
По диаметру dp = d1 подбирается диаметр болта d из стандарта
резьб.
157
158.
Глава 13. СВАРНЫЕ СОЕДИНЕНИЯ13.1. Общие сведения
Сварные соединения – неразъемные. Применяют электрическую, газовую, диффузионную, ультразвуковую сварку и
сварку взрывом и т.д.
Достоинства сварных соединений:
−
возможность получения изделий больших размеров
(мосты, корпуса судов и летательных аппаратов, железнодорожные вагоны, резервуары, фермы, кузова
автомобилей и др.);
−
снижение массы: по сравнению с литыми деталями
до 30 50%; по сравнению с заклепочными соединениями – до 20%;
−
снижение стоимости изготовления сложных деталей
в условиях единичного и мелкосерийного производства;
−
плотность и герметичность соединений;
−
малая трудоемкость, невысокая стоимость оборудования, возможность автоматизации.
Недостатки сварных соединений:
−
вероятность возникновения при сварке скрытых дефектов сварного шва (непровары, трещины, шлаковые включения);
−
трудность контроля качества сварного шва; существующие рентгеноскопические и ультразвуковые методы сложны;
−
коробление деталей из-за неравномерности нагрева в
процессе сварки;
−
невысокая прочность при переменных режимах нагружения, так как сварной шов является сильным
концентратором напряжений.
158
159.
По взаимному расположению соединяемых элементовсварные соединения разделяют на следующие виды:
1) стыковые соединения, когда соединяемые детали являются продолжением друг друга, сварку производят
по торцам (рис. 13.1). Обозначение на чертеже С1,
С2, …, С42;
Рис. 13.1. Сварное стыковое соединение
2)
нахлесточные соединения, когда боковые поверхности соединяемых элементов частично перекрывают
друг друга (рис. 13.2). Обозначение на чертеже Н1,
Н2, …, Н9;
Рис. 13.2. Сварное нахлесточное соединение
3)
4)
тавровые соединения, когда соединяемые детали перпендикулярны одна к другой или торец одного элемента
приварен к боковой поверхности другого (рис. 13.3,а).
Обозначение на чертеже Т1, Т2, …, Т9;
угловые соединения, когда соединяемые элементы
приваривают по кромкам друг к другу (рис. 13.3,б).
159
160.
Рис. 13.3. Соединения: тавровое (а) и угловое (б)13.2. Сварные соединения стыковыми швами
При стыковой сварке в зависимости от толщины деталей
сварку выполняют односторонним или двусторонними швами.
При толщине = 1 6 мм сварку производят без разделки
кромок (рис. 13.4,а), при 4 мм – со скосом различной формы
(рис. 13.4,б,в,г).
до 10 мм
до 60 мм и даже до 100 мм
до 120 мм
до 100 мм
Рис. 13.4. Разделка кромок сварного стыкового соединения
Стыковые швы рассчитываются на растяжение или сжатие:
F
р =
'p (МПа);
(13.1)
в
F
сж =
'сж (МПа).
в
160
161.
Допускаемые напряжения 'р и 'сж для сварных швовсм. ниже.
13.3. Сварные соединения угловыми швами
Нахлесточное соединение выполняется угловыми швами.
В зависимости от расположения эти швы могут быть лобовые,
фланговые, косые и комбинированные (рис. 13.5).
Рис. 13.5. Сварные нахлесточные соединения
Лобовой шов расположен перпендикулярно, а фланговый –
параллельно линии действия силы.
161
162.
Длина флангового шва принимается 30 мм < l 50К, где К– катет шва. Обычно принимают К = (или К = min, если толщины свариваемых деталей разные).
Угловые швы работают на растяжение и на срез (обозначение на чертеже У1, У2, …, У9). Разрушение углового шва происходит по сечению А-А, проходящему под углом 45о
(рис. 13.6). Условно такие швы рассчитываются на срез по наименьшему сечению шва (в этом случае h = 0,7К).
Рис. 13.6. Схема к расчету углового шва
Расчетное уравнение для фланговых швов имеет вид:
F
,
2 0,7 K L
(13.2)
L – суммарная длина фланговых швов (в данном случае –
см. рис. 13.7 L = 2l);
– допускаемое напряжение среза для угловых швов.
Лобовые швы, так же как и фланговые, рассчитываются на
срез по опасному сечению, проходящему под углом 45о.
Расчетное уравнение для лобового шва имеет вид (рис. 13.7,б):
где
F F (МПа).
0,7 K в 0,7 в
162
(13.3)
163.
Рис. 13.7. Сварные соединения фланговыми (а) и лобовым (б) швамиКомбинированное соединение фланговыми и лобовыми
швами (рис. 13.5) рассчитывают, считая, что сила F нагружает
швы равномерно
F
(МПа),
(13.4)
0,7 K (2l в)
где 2l+в – периметр комбинированных швов.
Для усиления фланговых швов (когда их длина недостаточна) применяются прорезные швы (рис. 13.8). Ширина прорезного шва принимается равной d = 2 , а длина l1 = (10 20) ,
l1max =25 .
Рис. 13.8. Сварное соединение прорезным швом
13.4. Допускаемые напряжения для расчета сварных
соединений
Допускаемые напряжения для расчета сварных соединений при статической нагрузке задают в долях от допускаемого
163
164.
напряжения на растяжение p основного металла свариваемых элементов (листов, полос, уголков и т.д.), (табл. 13.1).р т ,
(13.5)
S
где т – предел текучести основного металла;
S – коэффициент запаса: S = 1,3 1,6 – для низкоуглеродистой; S = 1,5 1,7 – для низколегированной стали.
Таблица 13.1
Метод сварки
Автоматическая
и механизированная под флюсом
Ручная дуговая электродами
Э42А и Э50А
Ручная дуговая электродами
Э38; Э42; Э50
Контактная точечная и шовная
Допускаемые напряжения
для сварных швов
Растяжение
Сжатие
Срез
'ср
'p
'сж
'p
'p
0,8 'p
'p
'p
0,65 'p
0,9 'p
'p
0,6 'p
-
-
0,5 'p
П р и м е ч а н и е: в обозначении электродов число, стоящее после буквы Э,
умноженное на 10, обозначает в шва (МПа).
Приведенные табличные данные пригодны для расчета
только при статических нагрузках. При переменных и знакопеременных нагрузках табличные значения умножаются на коэффициент < 1, т.е.
'перем 'стат и 'перем 'стат .
(13.6)
Значения = 0,7 0,9 при переменной нагрузке и = 0,6 0,75
при знакопеременной.
164
165.
13.5. Примеры расчетов сварных соединенийРасчет углового шва в тавровом соединении, нагруженного
крутящим моментом
Рис. 13.9. Приварка трубы
На рисунке 13.9 показано тавровое соединение трубы, нагруженной крутящим моментом.
В этом случае К , а может быть принят произвольно.
Можно считать, что напряжения Т равномерно распределены по кольцевой площадке разрушения шва (рис. 13.10).
Средний диаметр этой площадки равен
dср = D + 0,7К D.
Такой шов проще рассчитывать не на кручение, а на срез
по окружной силе Ft: Ft T и уравнение прочности сварного
D
2
шва будет таковым:
F
T
2T
t
'ср .
(13.7)
2
A D 0,7 K D 0,7 K D
2
Рис. 13.10. Расчетная схема
165
166.
Расчет угловых швов, если одна из соединяемых деталейасимметрична
Рассмотрим конструкцию, у которой уголок приварен к
листу (рис. 13.11).
Рис. 13.11. Приварка уголка
Предполагается, что сила F проходит через центр тяжести
поперечного сечения уголка. Полагая, что швы l1 и l2 испытывают одинаковые напряжения , можно записать:
F1 l1 h;
F2 l2 h,
т.е.
F1 l1
;
F2 l2
(13.8)
b
a
F и F2
F,
(13.9)
a b
a b
где F1 и F2 – сила, приходящаяся на каждый шов;
а и b – расстояния до центра тяжести уголка (приводятся в
ГОСТ).
Напряжение в обоих швах:
F
'ср (МПа).
(13.10)
0,7 K ( L1 L2 )
Для равнобоких уголков F1 0,7F и F2 0,3F, соответственно l1 = 0,7l и l2 = 0,3l, где l – суммарная длина фланговых
швов.
F1
166
167.
Общий случай расчета системы швов, нагруженных силойи моментом в плоскости стыка свариваемых деталей
(рис. 13.12)
Рис. 13.12. Общий случай расчета системы сварных швов
167
168.
Находим центр тяжести площади опасного сечения швов.В общем случае
Х ц.т.
F x
F у
; Х ц.т.
.
F
F
(13.11)
Переносим силу F в т. О с добавлением пары FF c моментом М = F L.
1. Напряжение среза в швах от центрально приложенной
силы F:
F
F
F
.
(13.12)
A 2 0,7 l 0,7 b
3. Напряжения в точках шва от момента М:
М 1, 2
М M rmax M r1
,
Wo
Jp
Jp
(13.13)
где M 1, 2 – максимальное напряжение в наиболее удаленной
точке, т.е. rmax = r1 = r2;
J p – полярный момент инерции площади опасных сечений шва относительно центра тяжести этой площади, мм4. Он
определяется как сумма моментов инерции относительно осей x
и y: J p J x J y .
Наибольшее суммарное напряжение возникает в т. 1 и в т. 2.
Оно определяется по формуле:
max F1 M 1 F2 1 M2 1 2 F1 M 1 cos 'ср .
168
(13.14)
169.
Глава 14. ЗАКЛЕПОЧНЫЕ СОЕДИНЕНИЯ14.1. Общие сведения
Заклепочные соединения относятся к неразъемным соединениям.
Преимущества заклепочных соединений по сравнению со
сварными:
− стабильность качества соединения; возможность
получения прочного плотного соединения;
− простота контроля качества соединения;
− возможность соединения деталей из несвариваемых материалов;
− возможность соединения деталей, нагрев которых
недопустим из-за коробления или отпуска термообработанных деталей;
− надежная работа при ударных и вибрационных нагрузках.
Недостатки:
− ослабление деталей отверстиями и в связи с этим
повышенный расход металла;
− неудобные конструктивные формы в связи с необходимостью наложения одной детали на другую
или применения накладок.
Преимущественно заклепками соединяются листовые конструкции.
Область применения:
− в авиа- и судостроении – обшивка фюзеляжа, корпуса;
− в современном пассажирском самолете их используют до 2,5 млн;
− в строительных сооружениях – мосты, фермы (для
строительства Крымского моста было использовано 760 тыс. заклёпок);
− в автомобилестроении – для рам грузовых автомобилей;
169
170.
−в общем машиностроении – для крепления зубчатых венцов к дискам колес, лопаток в турбинах,
фрикционных накладок, составных сепараторов
подшипников качения.
Наибольшее применение имеют заклепки со сплошным
стержнем и полукруглой головкой. Различают также заклепки с
плоской головкой и потайной головкой (в самолетостроении).
Заклепочные соединения разделяют на прочные (силовые)
и прочноплотные, обеспечивающие дополнительно и герметичность соединения.
По конструкции заклепочные соединения подразделяются
на виды:
− нахлесточные однорядные и многорядные (рис. 14.1);
Рис. 14.1. Нахлестное заклепочное соединение
−
стыковые с одной (рис. 14.2,а) или двумя (рис. 14.2,б)
накладками, однорядные или многорядные.
170
171.
Рис. 14.2. Стыковые заклепочные соединенияЗаклепочные соединения могут быть односрезные и многосрезные.
Диаметр заклепки можно принимать:
d 2 h (мм),
(14.1)
где h – суммарная толщина соединяемых элементов.
14.2. Расчет заклепки на прочность
Условия нагружения заклепок подобны условиям нагружения болтов, поставленных в отверстие без зазора. Тело заклепки работает на срез и на смятие.
Проверку прочности заклепки производят:
− по напряжениям среза
F
ср
4F ср (МПа);
(14.2)
2
2
d i
d iср
ср
4
− по напряжениям смятия
см F см (МПа),
d
171
172.
где iср – число поверхностей среза (на рис. 14.1 и 14.2,а iср = 1, ана рис. 14.2,б iср = 2).
Значения допускаемых напряжений принимают в зависимости от материала заклепки, способа обработки отверстий
(сверление или продавливание) и условий работы. Так, для заклепок из сталей марок ст2, ст3 при обработке отверстия сверлением и нормальных условий эксплуатации ср 140 МПа,
см 280...320 МПа. При продавливании отверстий и при холодной клепке допускаемые напряжения понижают на 20…30%.
Используя расчеты, приведенные в данном пособии, можно спроектировать привод к любому исполнительному механизму.
172
173.
СПИСОК ЛИТЕРАТУРЫ1.
Иванов М.Н., Финогенов В.А. Детали машин: Учебник.
– 9-е изд. – М.: Высшая школа, 2005. – 408 с.
2. Решетов Д.Н. Детали машин: Учебник. – 4-е изд. – М.:
Машиностроение, 1989. – 496 с.
3. Клоков В.Г., Курбатова И.А. Детали машин: Учебное
пособие для выполнения курсового проекта. – М.:
МГИУ, 2005. – 112 с.
4. Дунаев П.Ф., Леликов О.П. Конструирование узлов и деталей машин: Учебное пособие для студентов технических специальностей вузов. – 8-е изд. – М.: Академия,
2004. – 496 с.
5. Анурьев В.И. Справочник конструктора-машиностроителя: В 3-х тт. Т. 2. – 9-е изд., перераб. и доп. / Под
ред. И.Н. Жестковой. – М.: Машиностроение, 2006.
– 960 с.
6. Гулиа Н.В., Клоков В.Г., Юрков С.А. Детали машин:
Учебник для студентов учреждений среднего профессионального образования / Под общ. ред. Н.В. Гулиа.
– М.: ИЦ «Академия», 2004. – 416 с.
7. Клоков В.Г. Детали машин: Учебное пособие. – 2-е
изд., стереотипное. – М.: МГИУ, 2006. – 74 с.
8. Клоков В.Г. Расчет зубчатых передач: Учебное пособие.
Ч. 1. – 2-е изд., стереотипное. – М.: МГИУ, 2005. – 52 с.
9. Клоков В.Г. Расчет и проектирование деталей передач.
Ч. 2. – 2-е изд., стереотипное. – М.: МГИУ, 2005. – 55 с.
10. Клоков В.Г. Детали машин. Курсовое проектирование.
– М.: МГИУ, 2007. – 185 с.
173
174.
Учебное изданиеКлоков Виктор Георгиевич
ДЕТАЛИ МАШИН
И ОСНОВЫ КОНСТРУИРОВАНИЯ
Часть III
Учебное пособие
Редактор Н.А. Киселева
Компьютерная верстка Р.Д. Рахматуллоева
Оформление обложки А.М. Гришиной
Санитарно-эпидемиологическое заключение
№ 77.99.60.953.Д.006314.05.07 от 31.05.2007
Подписано в печать 28.04.2008
Формат бумаги 60 84/16. Изд. № 2-90/07
Усл. печ. л. 11,0. Уч.-изд. л. 11,75. Тираж 500. Заказ № 1235
Издательство МГИУ, 115280, Москва, Автозаводская, 16
www.izdat.msiu.ru; e-mail: izdat@msiu.ru; тел. (495) 677-23-15
По вопросам приобретения продукции
издательства МГИУ обращаться по адресу:
115280, Москва, Автозаводская, 16
www.izdat.msiu.ru; e-mail: izdat@msiu.ru; тел. (495) 677-23-15
Отпечатано в типографии издательства МГИУ
174
175.
115280, Россия, г.Москва, ул.Автозаводская, 16тел./факс: (495) 674-62-50, 677-21-82, 677-24-92, 677-23-15
WWW.IZDAT.MSIU.RU, e-mail: izdat@msiu.ru
ПРЕДЛАГАЕМ ВАШЕМУ ВНИМАНИЮ КНИГИ
Клепиков В.В., Голов В.А., Порошин В.В.
Качество изделий: Учебное пособие. – М.: МГИУ, 2006.
– 252 с.
Раскрываются параметры качества изделий, геометрические
и функционально-механические свойства поверхностного
слоя изделий. Значительное внимание уделяется геометрическим параметрам микронеровностей профиля. Раскрыты
новые направления в области трехмерного анализа топографии поверхностного слоя.
Аверьянов О.И., Аверьянова Г.И., Толмачев С.А.
Компоновки металлорежущих станков: Учебное пособие.
– М.: МГИУ, 2007. – 168 с.
Учебное пособие по дисциплине «Металлорежущие станки»
предназначено для студентов высших технических образовательных учреждений, обучающихся по специальности «Технология машиностроения».
Мороз В.Г.
Подшипники качения: Методические указания. – М.:
МГИУ, 2007. – 55 с.
Дана краткая характеристика, назначение, применение,
принципы выбора полей допусков и посадок подшипников
качения, примеры, необходимые справочные материалы.
Предназначено для выполнения курсовых работ по курсу
«Метрология, взаимозаменяемость стандартизация и сертификация».
Аверьянова И.О., Аверьянов О.И.
Кинематика металлорежущих станков: Учебное пособие.
– М.: МГИУ, 2006. – 52 с.
Учебное пособие подготовлено для студентов высших учебных заведений, обучающихся по специальностям «Технология машиностроения» и «Проектирование и эксплуатация
автоматизированного производства».
175
176.
115280, Россия, г.Москва, ул.Автозаводская, 16тел./факс: (495) 674-62-50, 677-21-82, 677-24-92, 677-23-15
WWW.IZDAT.MSIU.RU, e-mail: izdat@msiu.ru
ПРЕДЛАГАЕМ ВАШЕМУ ВНИМАНИЮ КНИГИ
Ульянина И.Ю.
Материаловедение в схемах и конспектах: Учебное
пособие. Ч. 1. – М.: МГИУ, 2006. – 113 с.
Курс представлен в виде логических схем, где материал
расположен в порядке увеличения сложности вопросов и
изучаемых тем. Учебное пособие является дополнительным
материалом к лекционному курсу по материаловедению.
Ульянина И.Ю.
Материаловедение в схемах и конспектах: Учебное пособие. Ч. 2. – М.: МГИУ, 2006. – 140 с.
Курс представлен в виде логических схем, где материал расположен в порядке увеличения сложности вопросов и изучаемых тем. Учебное пособие является дополнительным материалом к лекционному курсу по материаловедению.
Максимов Б.А., Наумов Л.И., Резниченко А.В., Усанова О.Ю.
Технологические процессы машиностроительного производства и технология конструкционных материалов: Лабораторный практикум. – М.: МГИУ, 2007. – 96 с.
В практикуме по курсу «Технология конструкционных материалов» изложены краткие теоретические сведения, необходимые для выполнения практической части лабораторных
работ. Указан порядок выполнения работ по холодной листовой штамповке, горячей обработке давлением, ручной дуговой и контактной сварке, токарной и фрезерной обработке.
Бадаев Ф.З., Стукалова Н.П., Хайри А.Х.
Кинетика химических реакций: Учебное пособие. – М.:
МГИУ, 2007. – 67 с.
В учебном пособии изложены основные кинетические закономерности протекания простых и сложных химических реакций,
приведены примеры решения задач и задачи для самостоятельного решения, дается описание лабораторной работы по изучению кинетики каталитического разложения пероксида водорода.
Предназначено для студентов специальности «Материаловедение в машиностроении».
176












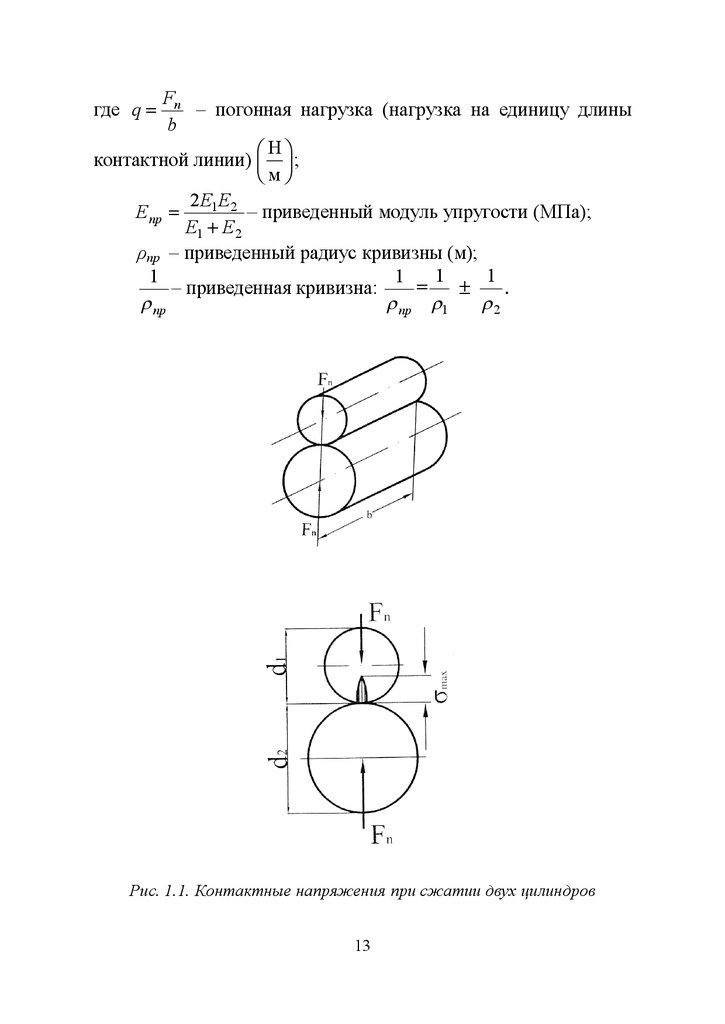
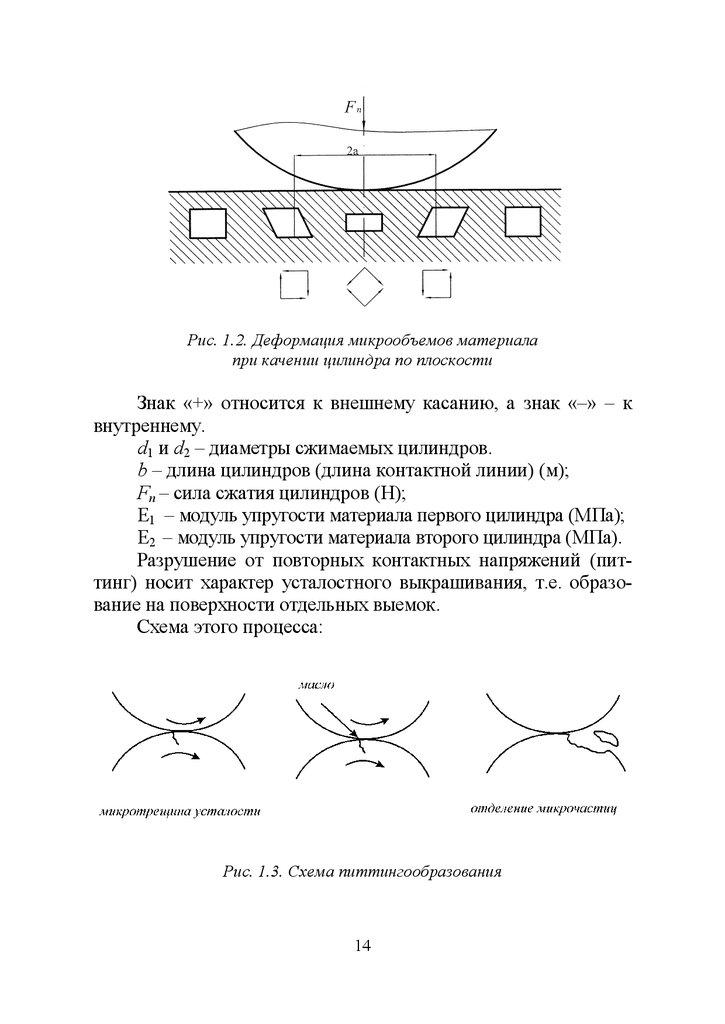




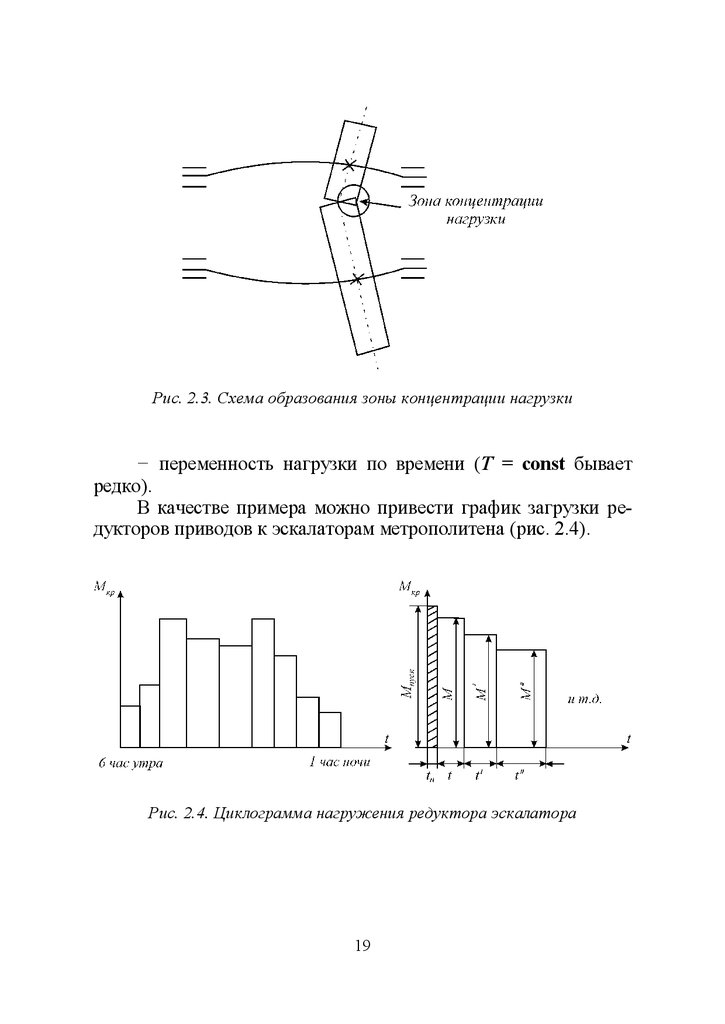

























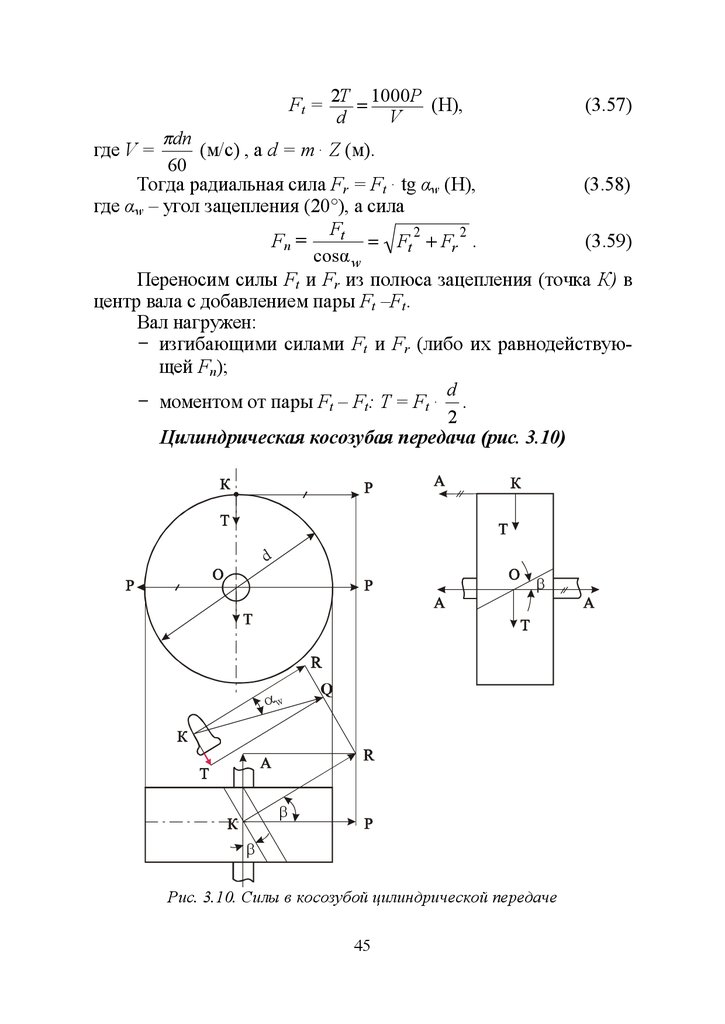




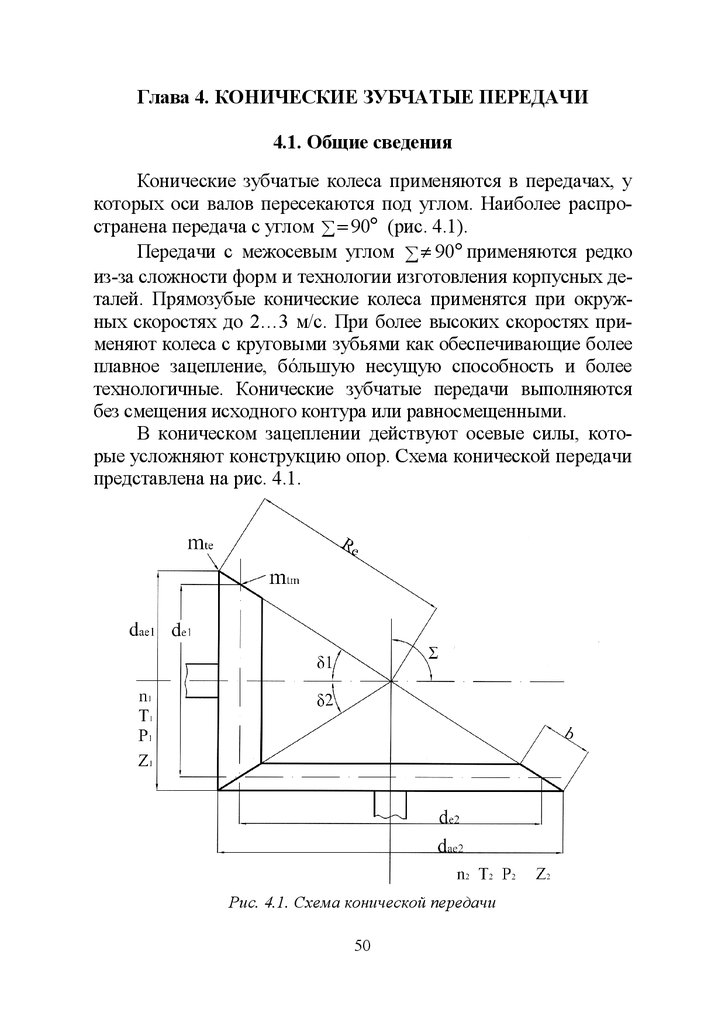
















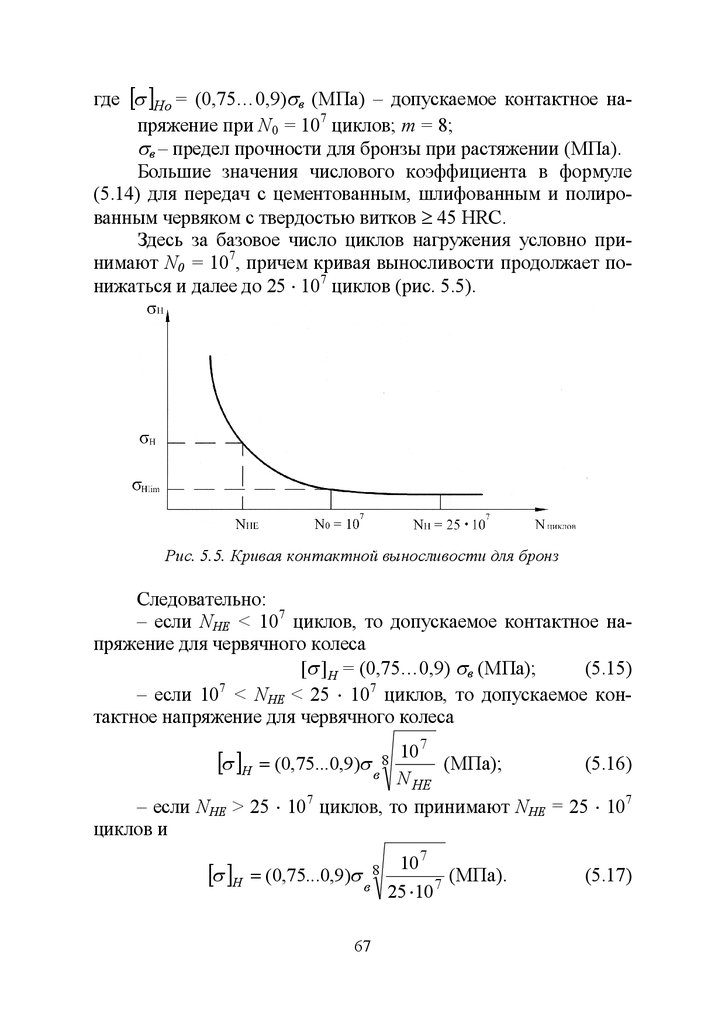














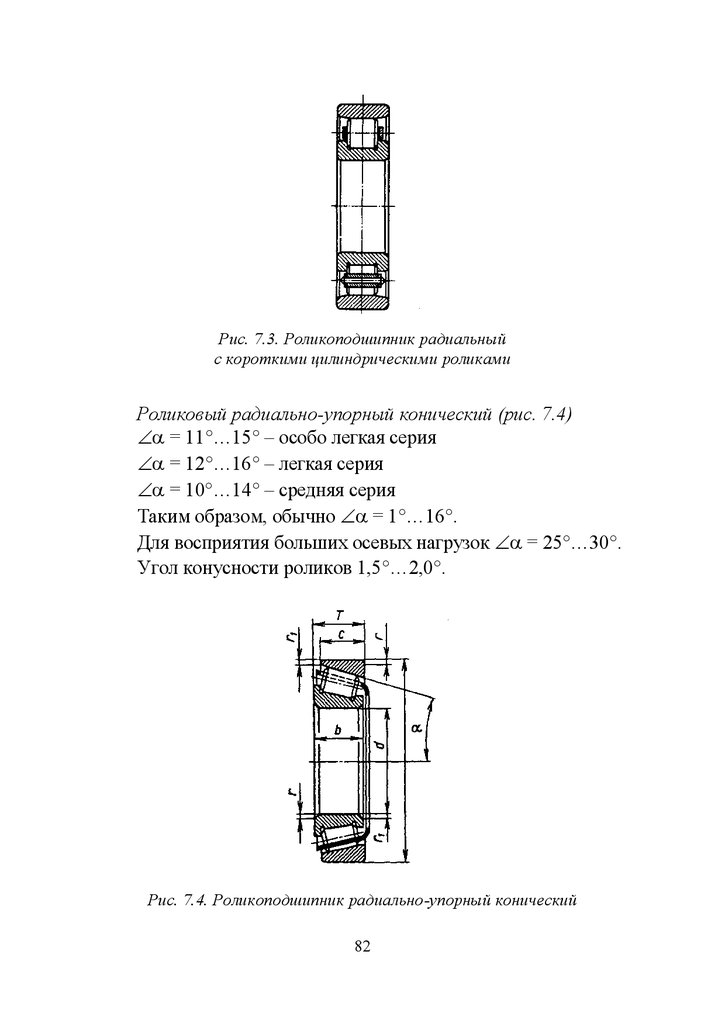























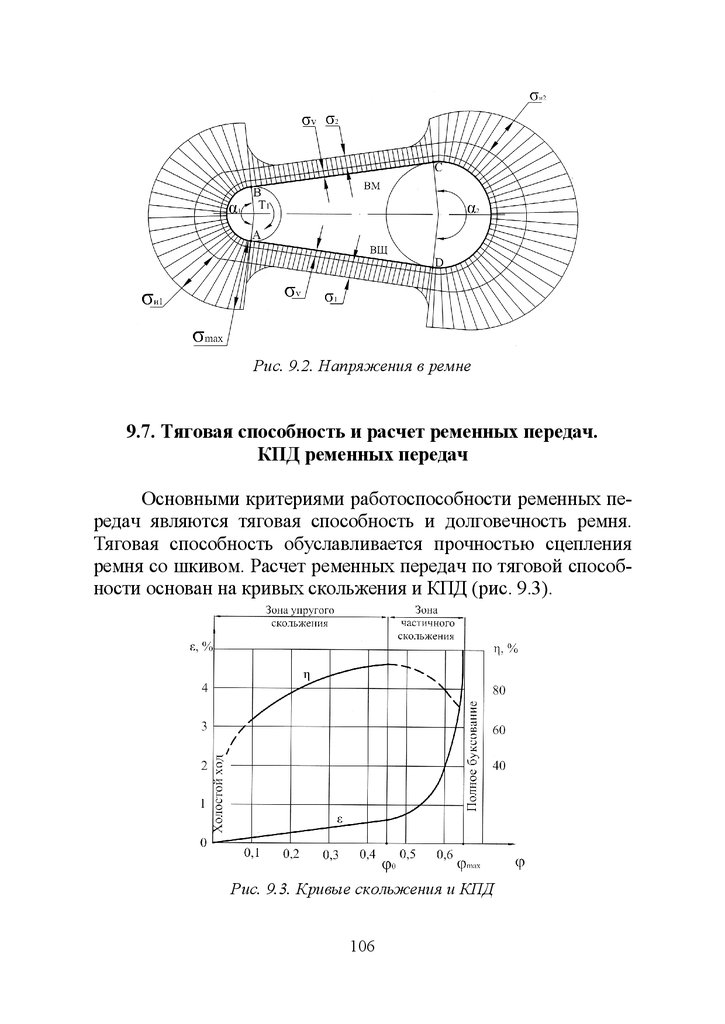


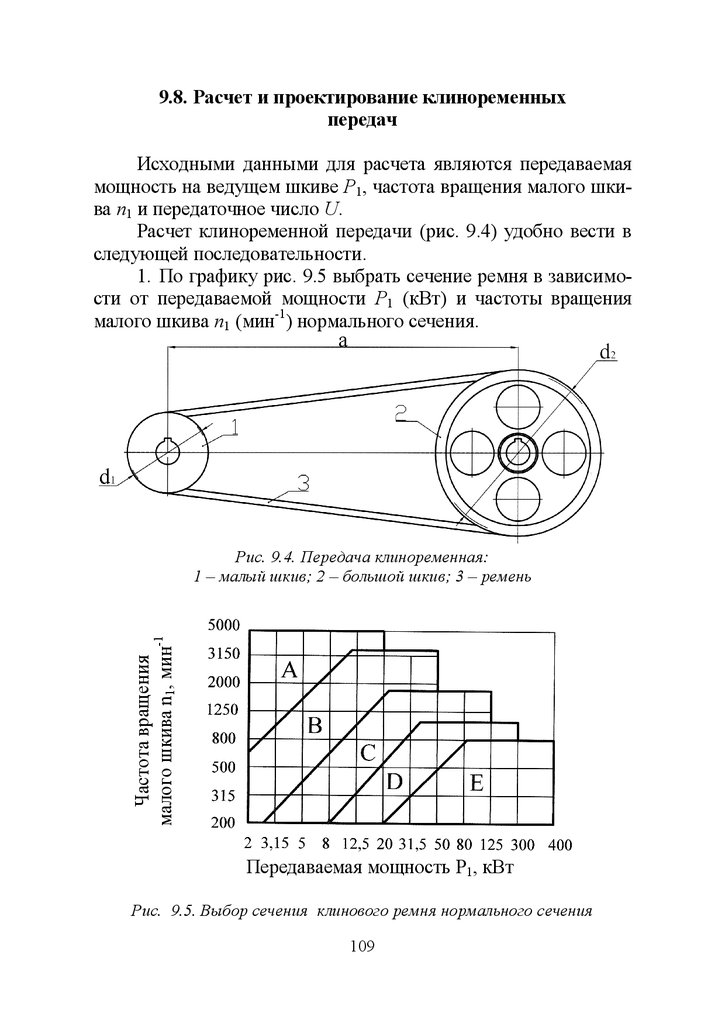






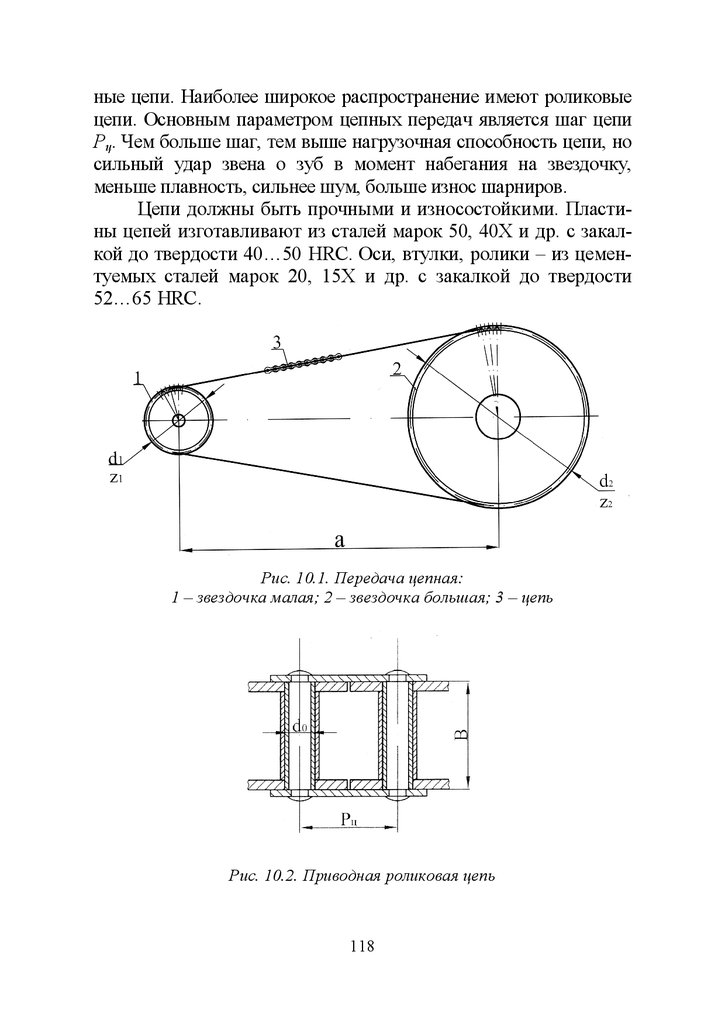

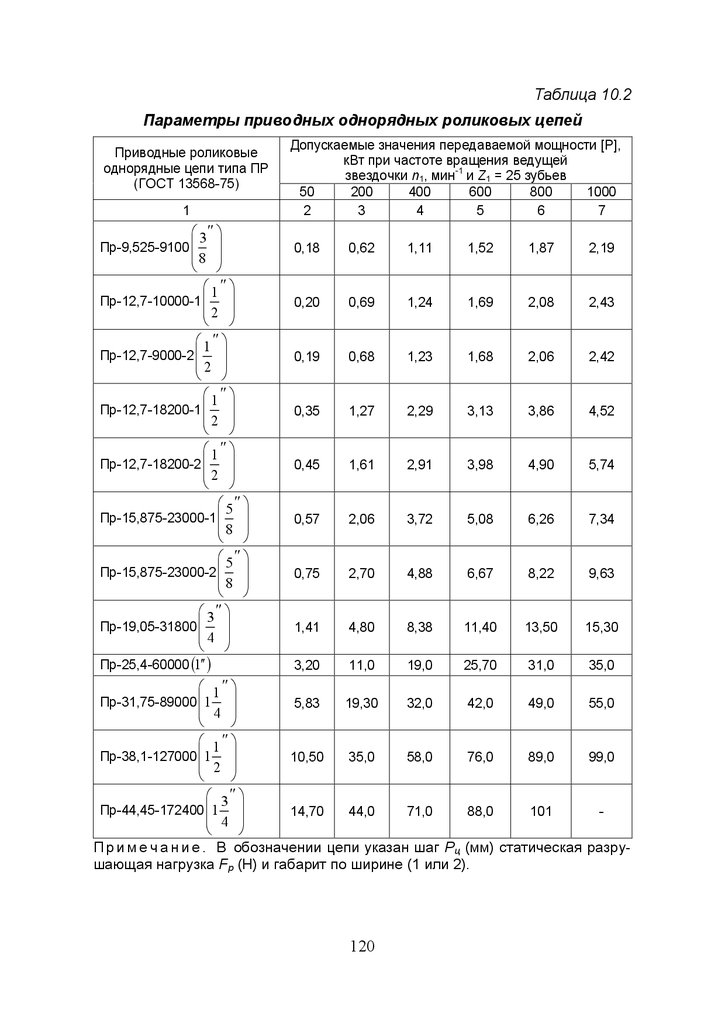














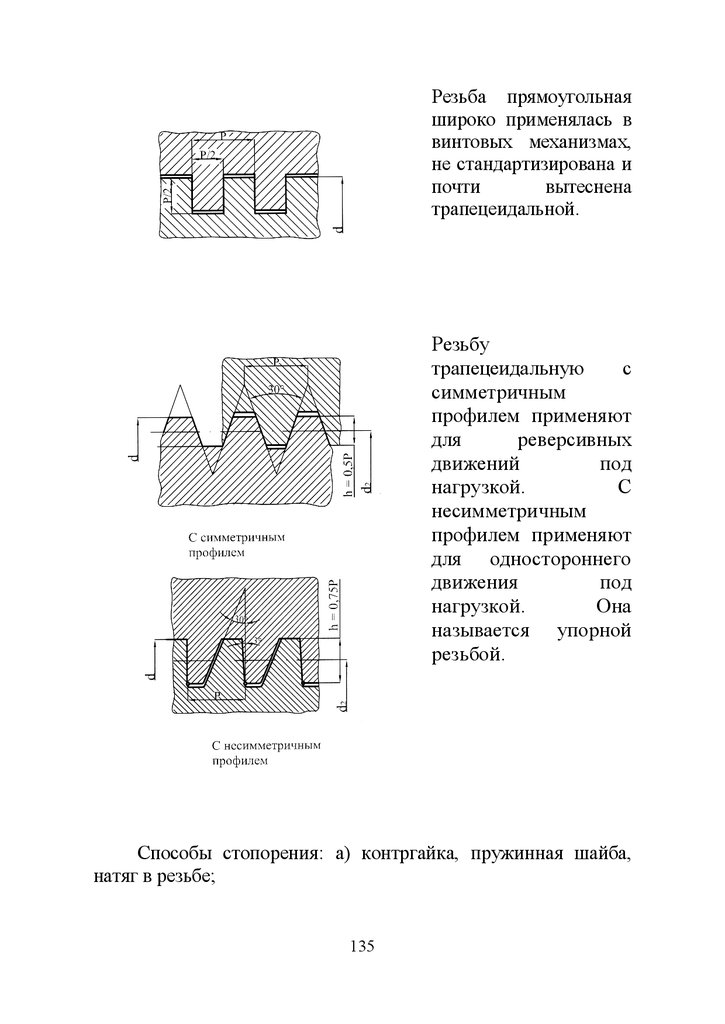


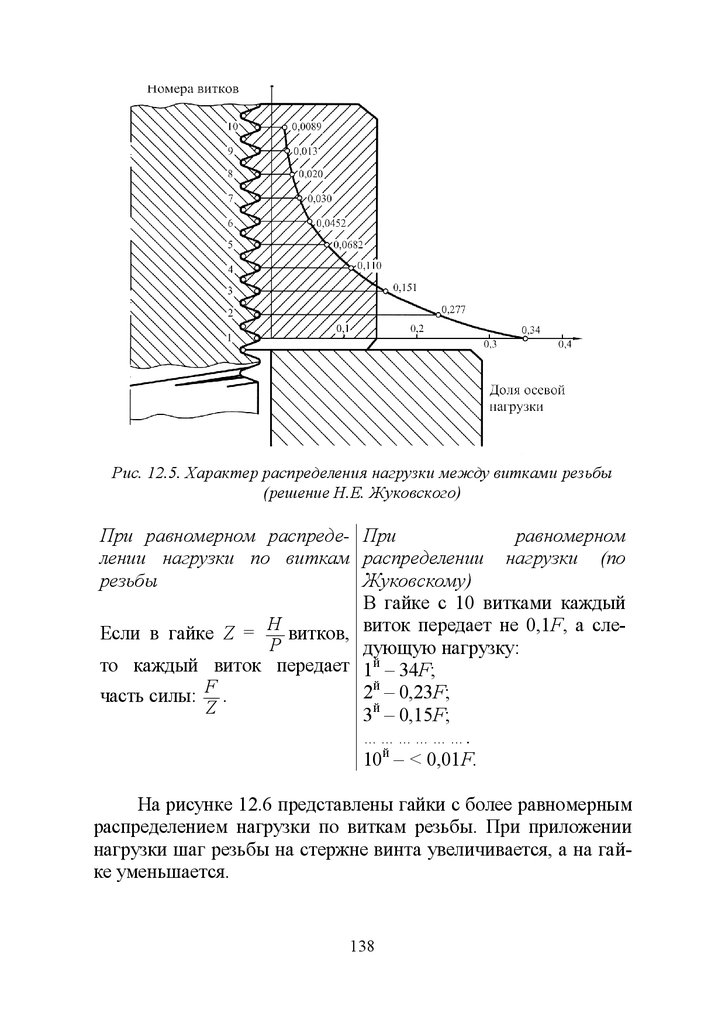
















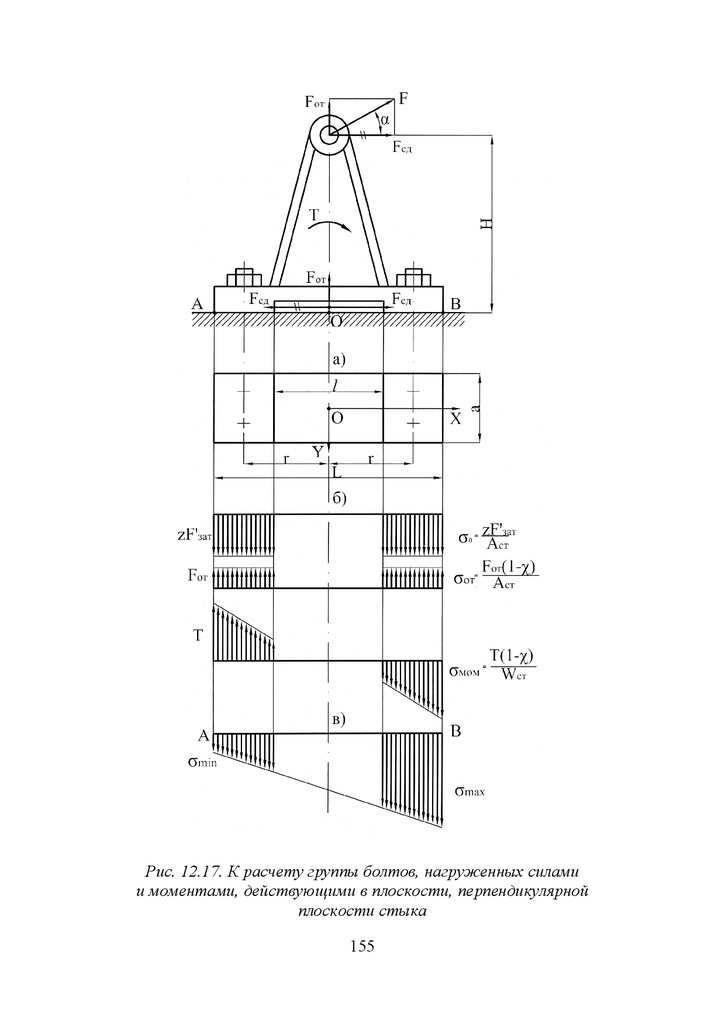











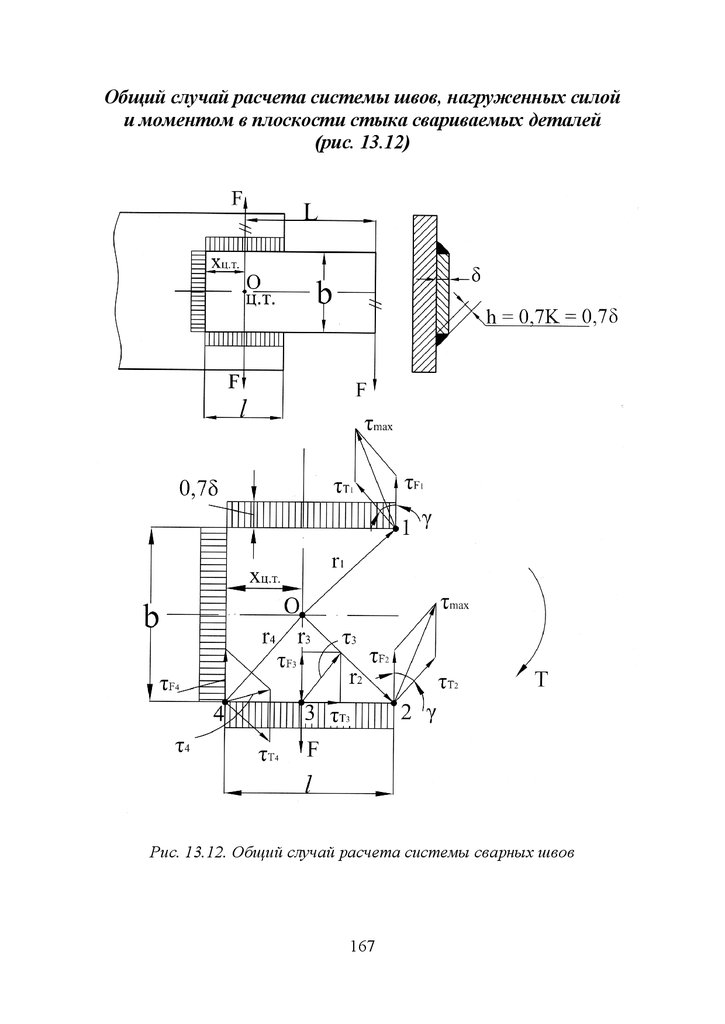


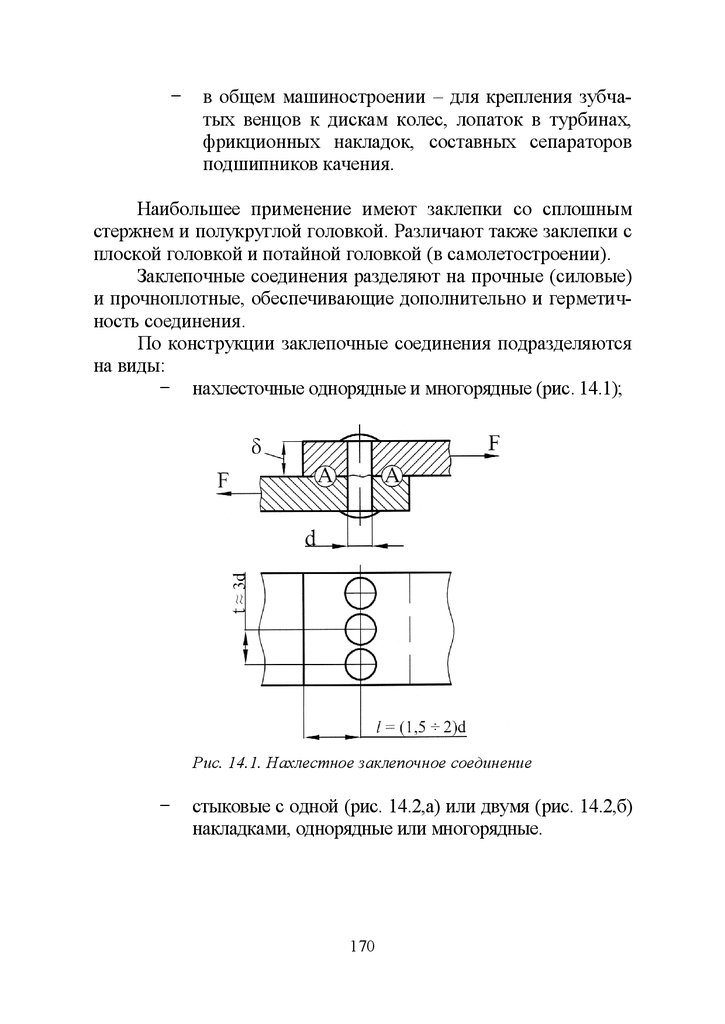






 mechanics
mechanics drafting
drafting








