Плоский изгиб. Деформации и перемещения балки

1.

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Лекции
по дисциплине «Техническая механика»
270800 - Строительство

2. Плоский изгиб Деформации и перемещения

3.

Определение деформации балки
Основные понятия и определения
При изгибе балка прогибается, т.е. в плоскости действия сил (плоскость
x0y) изменяется кривизна оси, и плоские поперечные сечения
поворачиваются и смещаются на некоторую величину относительно
нейтральной оси.
Искривленная
ось
балки
при
изгибе
называется изогнутой
осью или упругой
линией.
Деформация балки при изгибе описывается двумя параметрами:
1) прогиб (y, v) – смещение центра
тяжести
сечения
балки
по
направлению перпендикулярному
к ее оси.
Наибольший прогиб балки
называется стрелой прогиба
(f=ymax);
Не путать прогиб y с координатой y
точек сечения балки!

4.

2) угол поворота сечения
(φ) – угол, на который
сечение
поворачивается
относительно своего первоначального положения (угол
между
касательной
к
упругой
линии
и
первоначальной
осью
балки).
В общем случае величина прогиба балки в данной точке является
функцией координаты x и может быть записана в виде следующего
уравнения:
y y(x)
Тогда угол между касательной к изогнутой оси балки и осью x будет
определяться из следующего выражения:
dy
tg
dx
Ввиду малости углов и перемещений, можем считать, что
угол поворота сечения есть
первая производная от прогиба
балки по абсциссе сечения.
dy
dx

5.

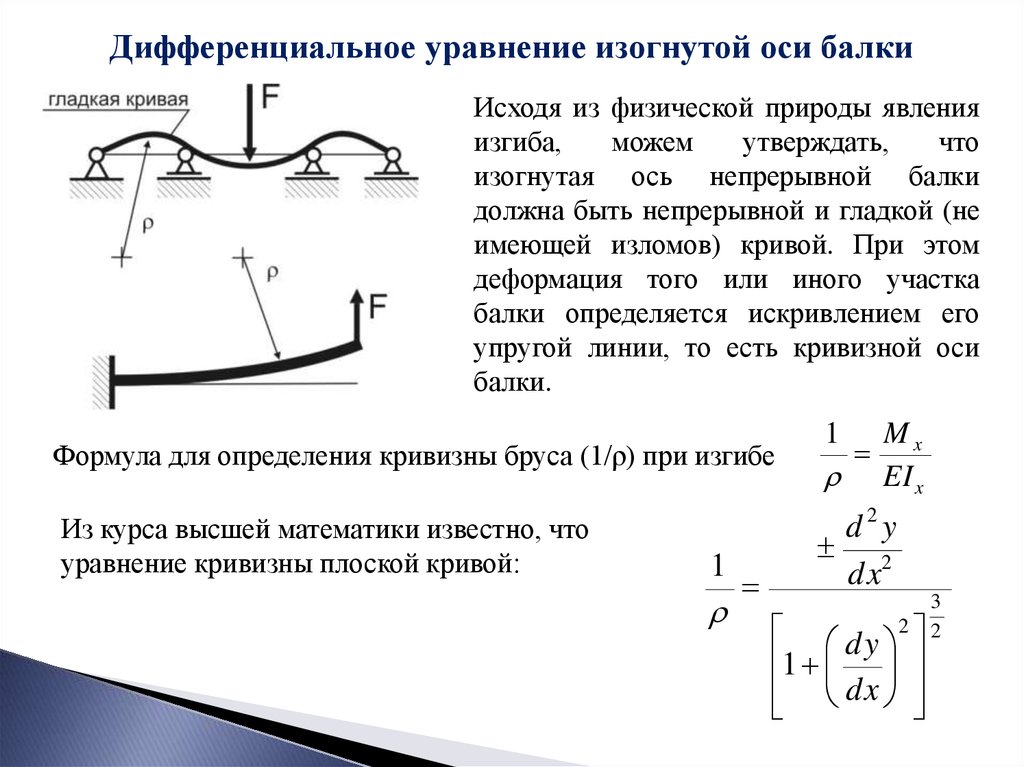
Дифференциальное уравнение изогнутой оси балки
Исходя из физической природы явления
изгиба,
можем
утверждать,
что
изогнутая ось непрерывной балки
должна быть непрерывной и гладкой (не
имеющей изломов) кривой. При этом
деформация того или иного участка
балки определяется искривлением его
упругой линии, то есть кривизной оси
балки.
Формула для определения кривизны бруса (1/ρ) при изгибе
Mx
EI x
Из курса высшей математики известно, что
уравнение кривизны плоской кривой:
d2y
2
dx
1
1
dy 2
1
dx
3
2

6.

Приравняв правые части данных выражений, получим дифференциальное
уравнение изогнутой оси балки, которое называется точным уравнением
изогнутой оси бруса.
d2y
dx2
dy 2
1
dx
3
2
Mx
EI x
В координатной системе прогибов x0y, когда ось y направлена вверх, знак
момента определяет знак второй производной от y по x.
Интегрирование данного уравнения, очевидно, представляет некоторые
трудности. Поэтому его, как правило, записывают в упрощенной форме,
пренебрегая величиной в скобках по сравнению с единицей.
Дифференциальное уравнение упругой линии балки
d2y Mx
2
EI x
dx

7.

Решение дифференциального уравнения найдем, интегрируя обе его части по
переменной x:
dy
dx
y
l
M x ( x)
dx C1
EI x
M x ( x)
dx C1 x D1
EI x
Постоянные интегрирования C1, D1 находят из граничных условий –
условий закрепления балки, при этом для каждого участка балки будут
определяться свои постоянные.
1. Метод непосредственного интегрирования

8.

Рассмотрим решения данных уравнений на конкретном примере.
Дано:
Консольная балка длиной l, загруженная поперечной
силой F. Материал балки (E), форму и размеры ее
сечения (Jz) также считаем известными.
Определить закон изменения угла поворота φ(x) и
прогиба y(x) балки по ее длине и их значения в
характерных сечениях.
Решение
а) реакции в заделке
Fy 0
RA F
M
A
0
MR F l
б) методом мысленных сечений определим
внутренний изгибающий момент
M x ( x) RA x M R F x F l

9.

в) определим угол поворота сечений
балки
Постоянную C1 найдем из условий закрепления, а именно – в жесткой
заделке угол поворота равен нулю, тогда
Найдем угол поворота
свободного конца балки
(x=l)
Знак «минус» показывает, что сечение
повернулось по часовой стрелке.

10.

г) определим прогибы балки
Постоянную D1 найдем из условий закрепления, а именно – в жесткой
заделке прогиб равен нулю, тогда
Найдем прогиб свободного конца балки (x=l)
Знак «минус» показывает, что сечение опустилось вниз.

11.

Использование изложенной техники определения перемещений для
балок, имеющих несколько участков, оказывается достаточно трудоемким,
так как для n участков число произвольных констант (C и D) возрастает до
2n.
Для уменьшения вычислительной работы в подобных случаях
разработан ряд методов, которые позволяют при любом числе участков
свести решение к отысканию всего двух констант – прогиба и угла
поворота в начале координат.
•Метод начальных параметров
•Теорема Кастильяно
•Метод Максвелла-Мора
•Формула Симпсона
•Способ Верещагина

12.

Универсальное уравнение упругой линии.
2. Метод начальных параметров
Правила метода:
1) начало координат необходимо выбирать общим
для всех участков в крайней левой (или правой)
точке балки;
2) все составляющие уравнения моментов на
предыдущем участке должны сохраняться
неизменными
в
уравнении
моментов
последующих участков;
3) в случае обрыва распределенной нагрузки ее
продлевают
до
конца
балки,
а
для
восстановления
действительных
условий
нагружения
вводят
«компенсирующую»
нагрузку обратного направления;
4) интегрировать уравнения на всех участках следует, не раскрывая скобок.

13.

Рассмотрим некоторый отрезок балки,
нагруженной произвольной системой
сил и моментов (реакции опор также
представляем как внешние силы), и
составим для нее уравнение моментов в
произвольном сечении:
Группируя подобные слагаемые, запишем данное уравнение в самом общем
виде:
aM, aF, aq – координаты точки приложения внешнего момента, силы или
начало распределенной нагрузки. Сомножитель (x–a) должен быть всегда
положительным, слагаемые с отрицательными значениями (x–a)
отбрасываются. Сомножитель (x–aM)0 равен единице, но он необходим для
сохранения подобия слагаемых при последующем интегрировании.

14.

Универсальные уравнения для определения углов и прогибов балки при
изгибе:
Покажем, что C1 и D1 являются единственными константами, причем
где φ0, y0 – угол поворота и прогиб балки в начале координат.

15.

Рассмотрим два участка балки,
загруженной
произвольной
нагрузкой. Составим для обоих
участков универсальное уравнение
углов:
Для определения постоянных интегрирования CI и CII воспользуемся
граничными условиями. Тогда, при x=0 (из первого уравнения):
На границе участков (x=a) угол поворота
должен быть одинаков, то есть при x=a
должно быть φI(x=a)=φII(x=a):

16.

тогда
Проводя аналогичные рассуждения для уравнений, описывающих прогиб
балки на двух соседних участках и на их границе, найдем, что
Универсальные уравнения метода начальных параметров:

17.

Величина φш – угол поворота в
промежуточном (подвесном) шарнире,
при этом aш – координата шарнира.
Окончательный вид уравнений:
Pi Z a Pi
EI X ( Z ) EI X 0 mi ( Z a mi )
EI X Y ( Z ) EI X Y0 EI X 0 Z
mi Z a mi
2
2
2
2
Pi Z a Pi
6
3
qi Z a mi
3
6
qi Z a qi
4
24
При решении задач удобно записать универсальные уравнения сначала для
наиболее удаленного от начала координат участка, тогда уравнения для
предыдущих участков легко получить, вычеркивая из полученного
уравнения члены, учитывающие нагрузку на последующих участках.

18.

a)
МA
q =20 кН/м
A
RA
P =10 кН
1,2 м
2
1
0,8 м
б)
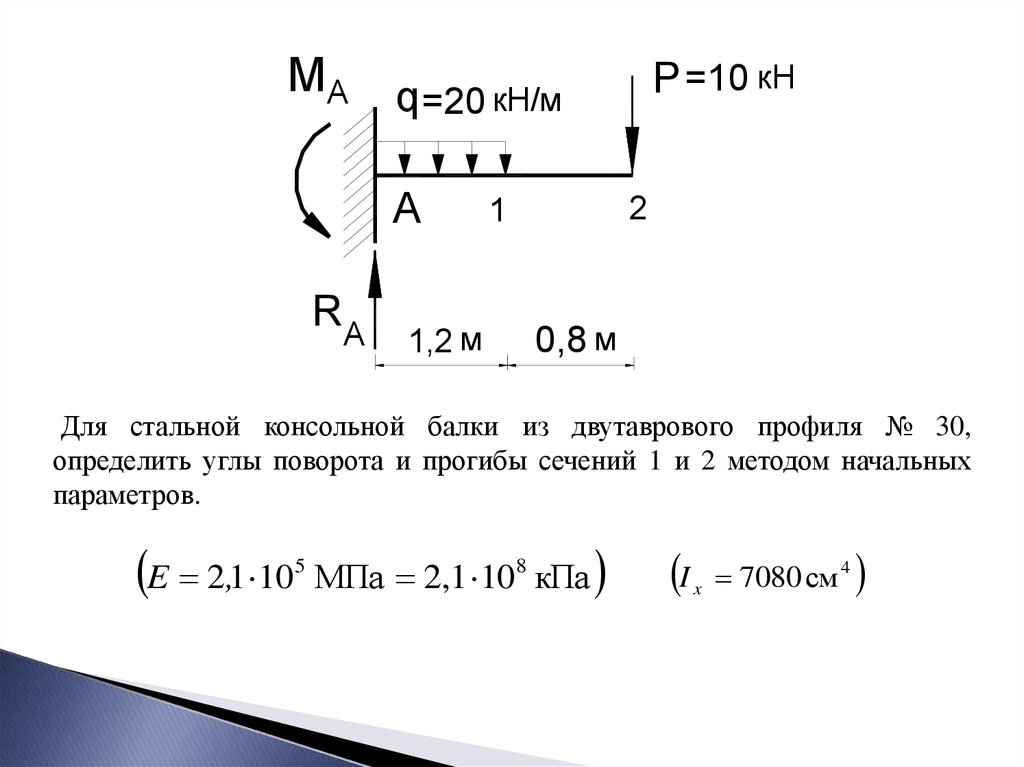
Для стальной консольной балки из двутаврового профиля № 30,
определить углы поворота и прогибы сечений 1Pи 2 методом начальных
A
q
параметров.
М
E 2,1 10
5
МПа 2,1 108 кПа
RA
q
I
x
7080 см 4

19.

Решение:
Из условия равновесия балки определяем опорные реакции:
M A 34,4 кН м;
mA M A q 1,2 0,6 P 2 0
y R
a
a)
Ra 34 кН.
q 1,2 P 0
Для определения перемещений балки в сечениях
1 и 2 начало координат
=10 кН
М
P
A
q =20балки
кН/мнам известны
принимаем на опоре А, так как из граничных условий
угол поворота и прогиб в этом сечении. Опора А – жесткое защемление,
следовательно, при z=0 A=0, yA=0.
2
1
A
Для применения формул метода начальных параметров
RA
1,2 м
0,8 м
б)
преобразуем заданные силы.
МA
P
q
RA
q

20.

Угол поворота и прогиб сечения 1 определяем из уравнений 1-го участка
при z=1,2 м:
1,2 2
1,2 3
2
EI 1 Ra
2
M A 1,2 q
3
6
22,56 кН м
1,2
1,2
1,2 4
EI y1 Ra
MA
q
16,664 кН м -3
6
2
24
22,56
16,664
3
3
1
1
,
52
10
рад.
y
1
,
12
10
м.
1
8
8
8
8
2,1 10 7080 10
2,1 10 7080 10
Угол поворота и прогиб сечения 2 определяем из уравнений 2-го
участка при z=2,0 м:
3
22
23
2 1,2
EI 2 Ra
MA 2 q q
25,763 кН м 2
2
2
6
6
2 1,2 36,455 кН м -3
2
2
2
EI y 2 Ra
MA
q
q
2
2
24
24
3
2
2
25,763
3
1
,
733
10
рад.
8
8
2,1 10 7080 10
4
y2
4
36,455
2,45 10 3 м .
8
8
2,1 10 7080 10
Углы поворота сечений 1 и 2 имеют положительные
следовательно, они поворачиваются по ходу часовой стрелки.
знаки,
Прогибы y1 и y2 имеют положительные знаки,
следовательно, они перемещаются вниз.