Similar presentations:
Изгиб. Основные понятия
1.
ИЗГИБ2.
ИЗГИБИзгиб - наиболее частый случай нагружения
различных систем.
Деформацию изгиба испытывают оси и валы
транспортных средств, рельсы, детали машин,
механизмов и строительных сооружений.
Именно изгиб часто является причиной поломок, разрушений и аварий.
3.
ИЗГИБОсновные понятия
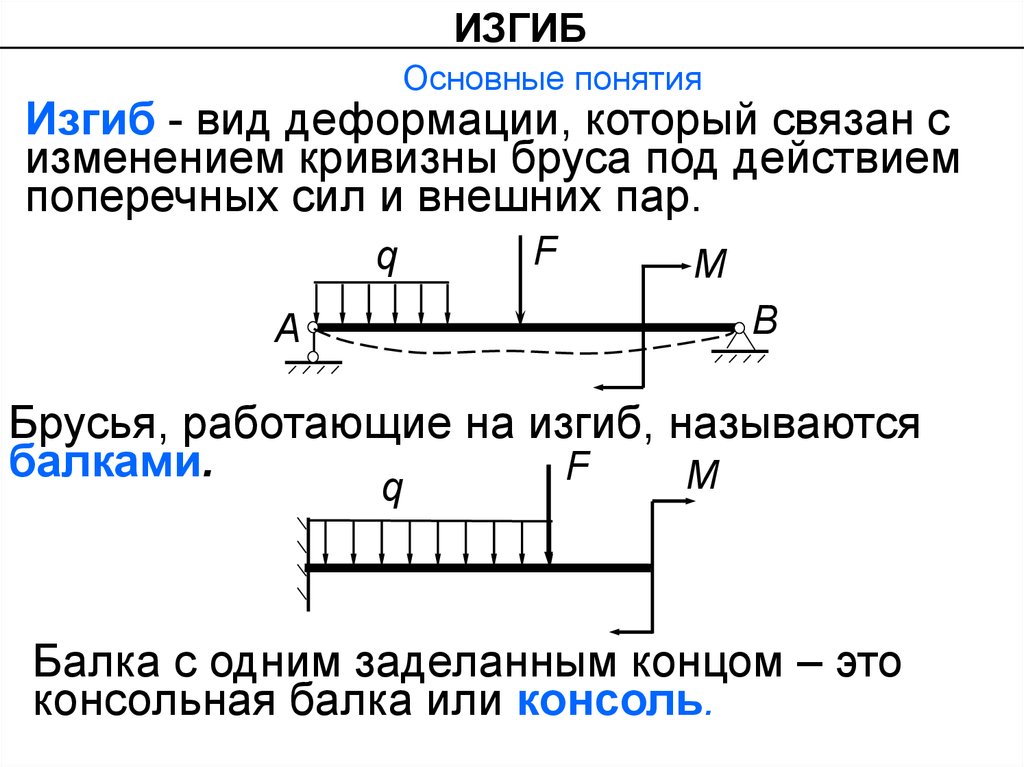
Изгиб - вид деформации, который связан с
изменением кривизны бруса под действием
поперечных сил и внешних пар.
q
F
М
B
А
Брусья, работающие на изгиб, называются
балками.
F
М
q
Балка с одним заделанным концом – это
консольная балка или консоль.
4.
ИЗГИБЕсли в поперечном сечении действует только
изгибающий момент, деформация называется чистый изгиб.
Изгиб от поперечных нагрузок называют
поперечным.
Поперечный изгиб может быть плоским прямым или косым изгибом.
F
F
F
Плоский изгиб происходит в случае, когда силовая плоскость (плоскость
действия изгибающего
момента) проходит через
одну из главных осей
инерции
5.
ИЗГИБРасчет на изгиб начинается с выбора расчетной схемы
При изгибе для закрепления балки, в основном, используются следующие связи:
стержень с шарнирами на концах (шарнирноподвижная опора)
цилиндрический шарнир (шарнирно-неподвижная опора),
жесткая заделка.
6.
ИЗГИБОпределение реакций
Для плоской системы сил достаточно 3-х уравнений статики. Так как все силы действуют перпендикулярно продольной оси балки, горизонтальная составляющая реакции равна нулю.
Для балки на двух опорах обычно используется следующая система уравнений:
у
М( А ) 0
YА
А
q
F
М
YB
B z
М( В ) 0
Fky 0
Третье уравнение используют для проверки
правильности определения реакций
7.
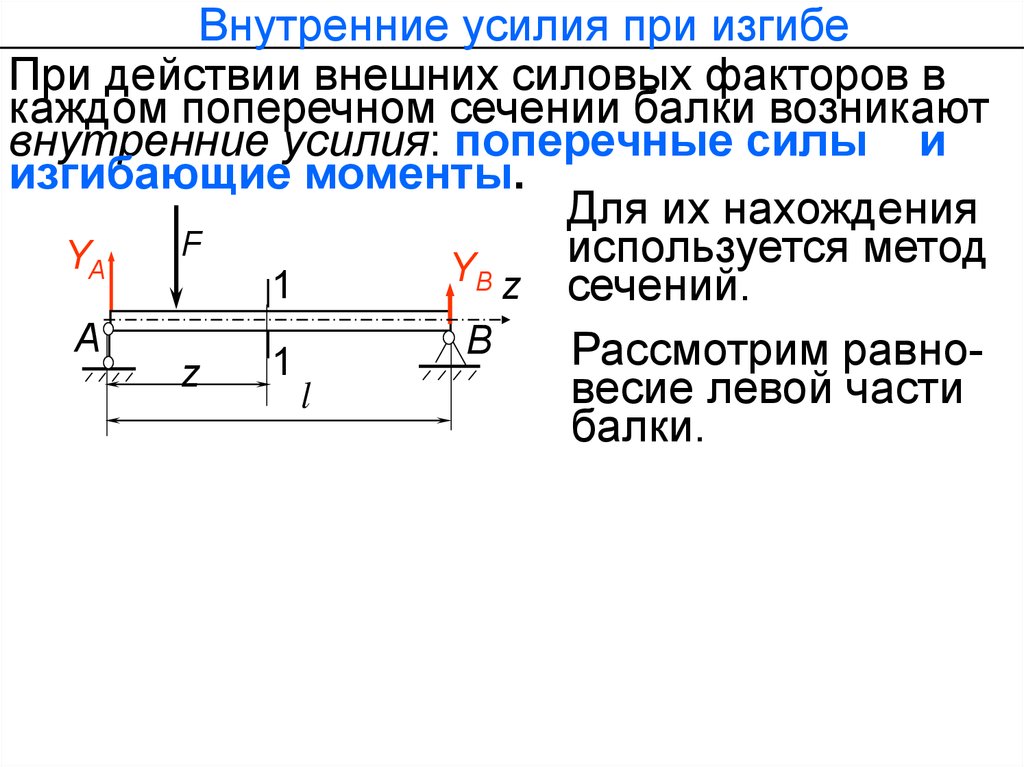
Внутренние усилия при изгибеПри действии внешних силовых факторов в
каждом поперечном сечении балки возникают
внутренние усилия: поперечные силы и
изгибающие моменты.
Для их нахождения
F
используется метод
YA
Y
Bz
1
сечений.
А
B
Рассмотрим
равно1
z
весие левой части
l
балки.
8.
Внутренние усилия при изгибеО - центр сечения
Выполним приведение систеO мы сил к центру сечения О
F
YA a
А
z
F
YA
А
a
O
z
F
a
YA
А
z
O
Qz
Mz
Cистему внешних сил можно
выразить через главный вектор, равный сумме внешних
сил и главный момент, равный
сумме моментов внешних сил
относительно центра сечения.
9.
FYA a
А
z
Внутренние усилия при изгибе
Запишем условие равновесия:
O
Mz
Qz
1)ΣМо= 0; Мz - YA·z + F·(z-a) = 0;
2)ΣFky= 0; -Qz + YA- F = 0
Мz= YA·z - F ·(z - a)
Qz = YA- F
Изгибающий момент Мz в любом сечении
равен алгебраической сумме моментов всех
сил, действующих по одну сторону от сечения
балки относительно центра тяжести сечения.
Поперечная сила Qz в любом сечении равна
алгебраической сумме проекций всех внешних сил, приложенных с одной стороны от сечения на ось в плоскости сечения, перпендикулярную к продольной оси балки.
10.
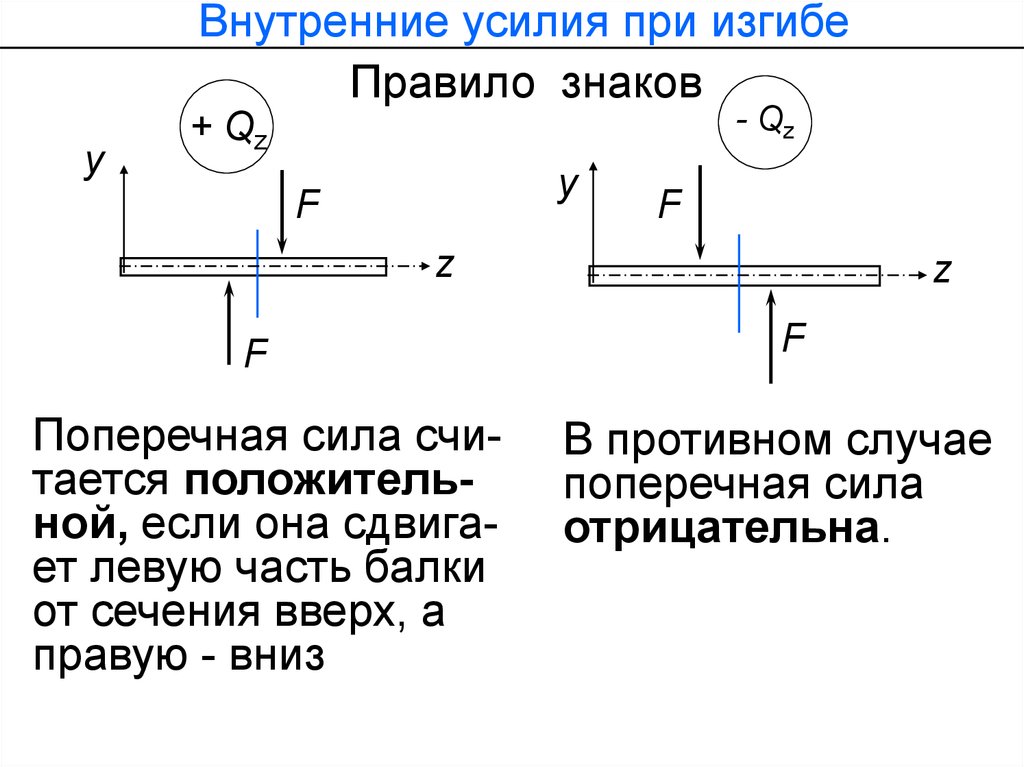
Внутренние усилия при изгибеПравило знаков
y
- Qz
+ Qz
y
F
F
z
F
Поперечная сила считается положительной, если она сдвигает левую часть балки
от сечения вверх, а
правую - вниз
z
F
В противном случае
поперечная сила
отрицательна.
11.
MВнутренние усилия при изгибе
Правило знаков
+ Mz
Изгибающий момент в
сечении
считается
полоM
жительным, если он
изгибает балку выпуклостью вниз: сжатые волокна вверху.
- Mz
M
M
При изгибе балки выпуклостью вверх изгибающий момент считается отрицательным.
12.
Дифференциальная зависимость между q, Q и MF
q
YA
А
z
dz
YB
B
На балку, лежащую на двух
опорах, действует распределенная нагрузка.
Вырежем двумя сечениями
элемент балки длиной dz.
Рассмотрим равновесие элемента
q О 1)ΣFky=0; Q–Q–dQ– qdz=0
1
М Q О
М+dМ
dz Q+ dQ
13.
Дифференциальная зависимость между q, Q и MМ Q О
М+dМ
2) ΣМо=0;
dz Q+ dQ
- М – (Q + dQ)dz– qdz·dz/2 + М+dМ = 0;
- М – Qdz -dQdz– qdz·dz/2 + М+dМ = 0;
Слагаемыми второго порядка малости можно
пренебречь
и
14.
Порядок построения эпюр1.Балка вычерчивается в выбранном масштабе с указанием размеров и нагрузок;
2. Определяются реакции с обязательной проверкой;
3. Балка разбивается на отдельные участки
со своим законом нагружения;
4. Для каждого участка записываются уравнения для определения Qz и Мz;
5. Вычисляют ординаты Qz и Мz по составленным для участков уравнениям;
6. Строят в принятом масштабе эпюры Qz и
Мz, откладывая вверх от оси балки положительные значения, вниз - отрицательные.
15.
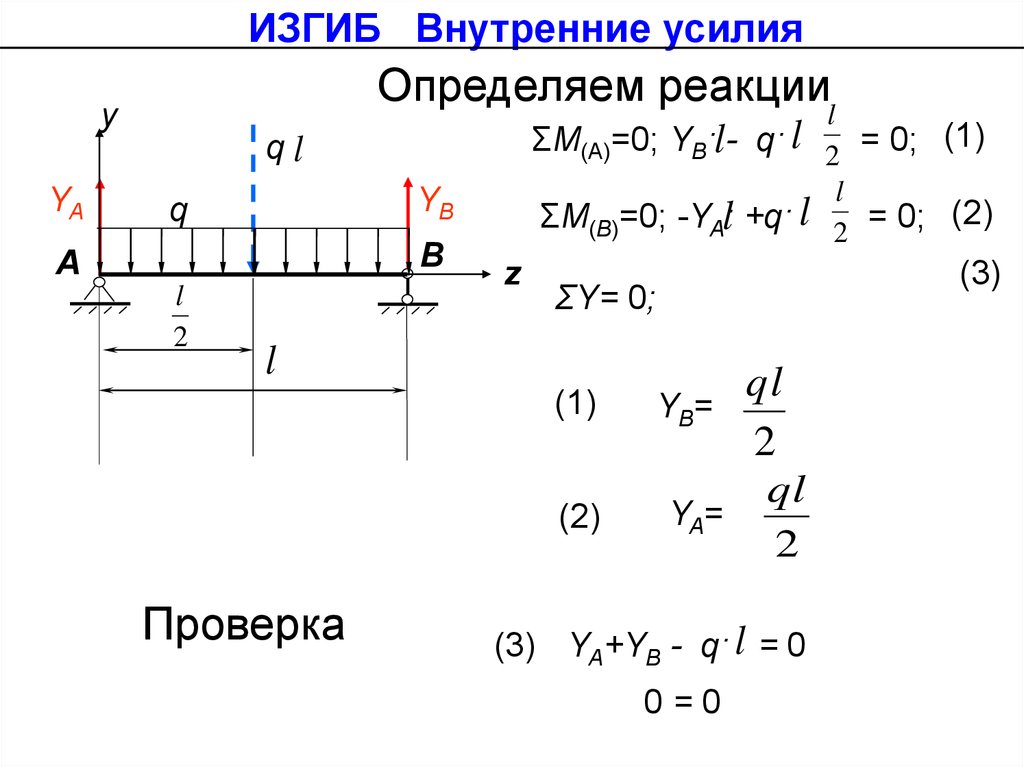
ИЗГИБ Внутренние усилияОпределяем реакции
y
ΣМ(А)=0; YB·l- q· l
ql
YA
YB
q
B
A
l
2
ΣМ(B)=0; -YAl· +q· l
z
(1)
(2)
Проверка
(3)
ΣY= 0;
l
l
(1)
2 = 0;
l
(2)
2 = 0;
ql
YB=
2
YA=
ql
2
(3) YA+YB - q· l = 0
0=0
16.
ИЗГИБ Внутренние усилия ПримерыРазбиваем балку на участки
y
1
YA
1
YB
1 q
A
B
z1
1
l
z1=0; z1= l
Участок один, так как характер
нагрузки не меняется
y
z
YA
1
1 q
A
Mz1
z
z1
ΣY= 0;
-Qz1- qz1+ YA= 0
ΣМ(o)=0; -YA·z1+ q·
Qz1 = YA- qz1
Qz1
2
z1
2
+Mz1 = 0;
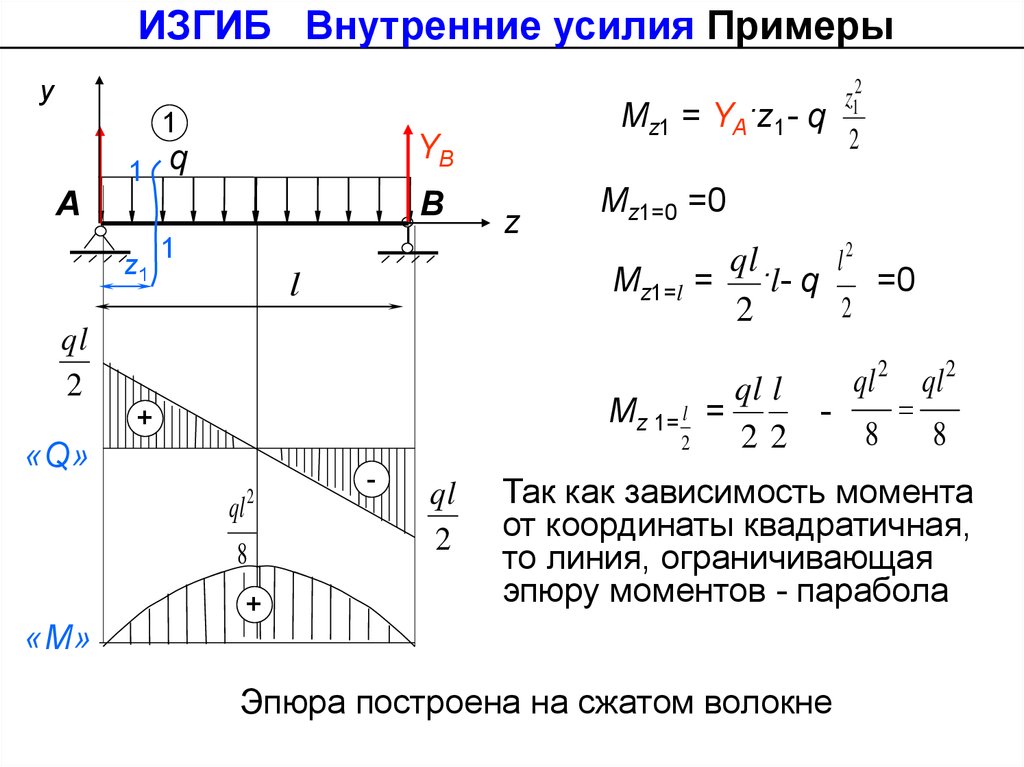
Mz1 = YA·z1- q
2
z1
2
17.
yИЗГИБ Внутренние усилия Примеры
1
1
1 q
YB
Qz1 = YA- qz1
Подставим значения координат и рассчитаем величину
A
B
z поперечной силы на концах
1
z1
участков
l
ql
Qz1=0 = YA=
;
ql
2
2
ql
ql
+
Qz1=l = YA-ql =
- ql =;
2
2
«Q»
ql Поперечная сила по длине участка принимает значение равное
2 нулю, а так как поперечная сила
– первая производная изгибающего момента, то момент будет
иметь в этой точке экстремальное значение
YA- qz1 = 0
Найдем координату, при которой Q=0.
ql
l
z1 = YA/q= 2q =
2
18.
ИЗГИБ Внутренние усилия Примерыy
1
YB
1 q
A
B
z1
1
z
Mz1=0 =0
l2
ql
Mz1=l = ·l- q
=0
2
2
l
ql
2
M
+
«Q»
ql
2
8
«М»
Mz1
+
z12
= YA·z1- q
2
-
ql
2
ql 2
z 1= l
2
ql 2
ql l
=
8
8
22
Так как зависимость момента
от координаты квадратичная,
то линия, ограничивающая
эпюру моментов - парабола
Эпюра построена на сжатом волокне
19.
ИЗГИБ Внутренние усилия Примерыy
YA
F
2
1
YB
B
A
l
l
ΣМ(А)=0; YB·l- F· 2
= 0; (1)
l
ΣМ(B)=0; -YA·l + F 2= 0; (2)
z
(3)
ΣY= 0;
(1)
(2)
F
YB=
2
F
YA=
2
Проверка
(3) YA+YB -
F =0
0=0
20.
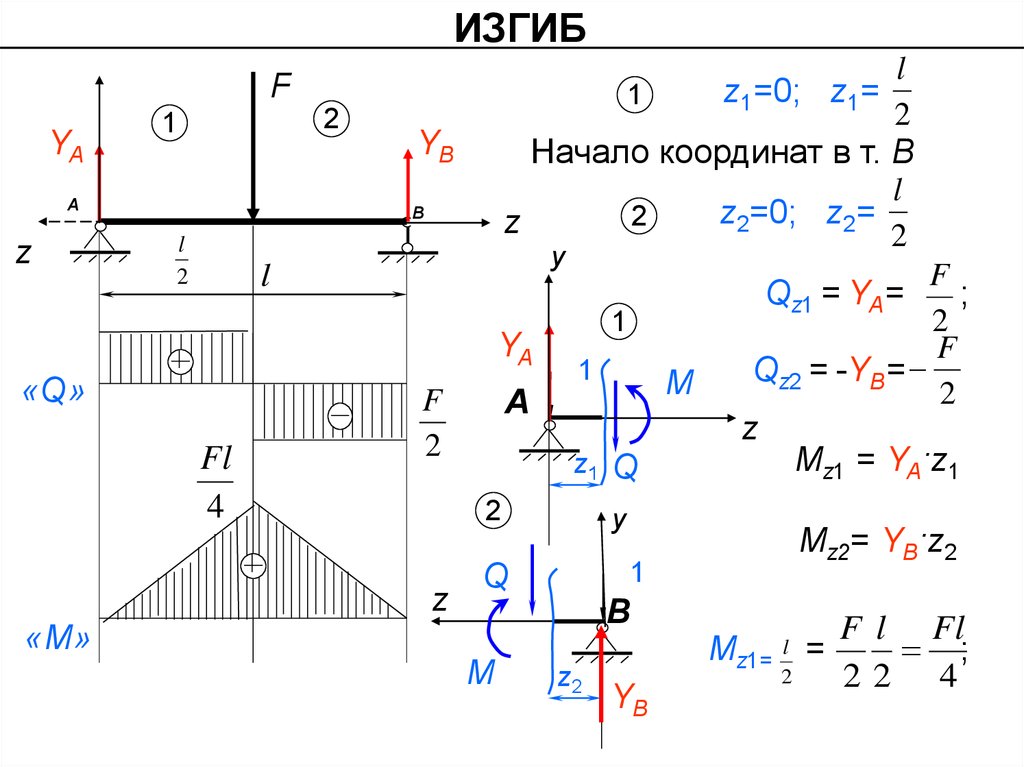
ИЗГИБl
z1=0; z1=
1
2
Начало координат в т. В
l
z2=0; z2=
2
z
2
F
YA
2
1
A
z
YB
B
l
2
y
l
YA
«Q»
Fl
4
«М»
F
2
1
1
M
A
z
Mz1 = YA·z1
z1 Q
2
z
F
;
2
F
Qz2 = -YB=
2
Qz1 = YA=
y
1
Q
M
Mz2= YB·z2
В
z2
YВ
Мz1= l =
2
F l Fl
;
22 4
21.
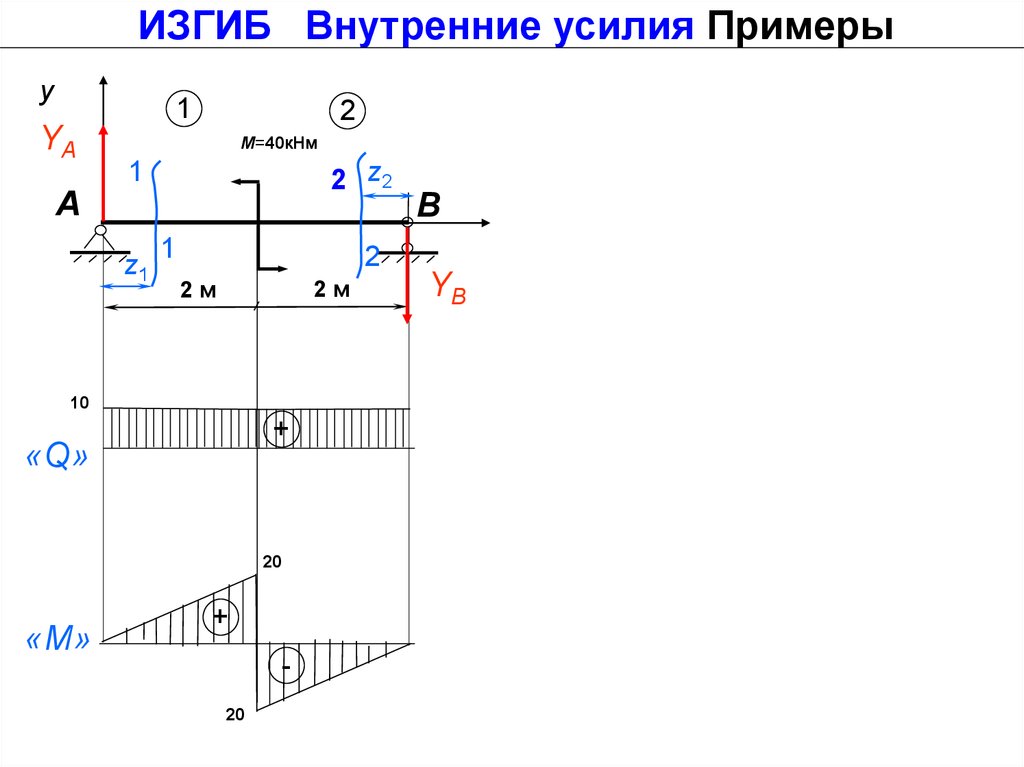
ИЗГИБ Внутренние усилия Примерыy
1
YА
2
М=40кНм
2 z2
1
A
z1
1
2
2м
2м
10
+
«Q»
20
«М»
+
20
B
YB
22.
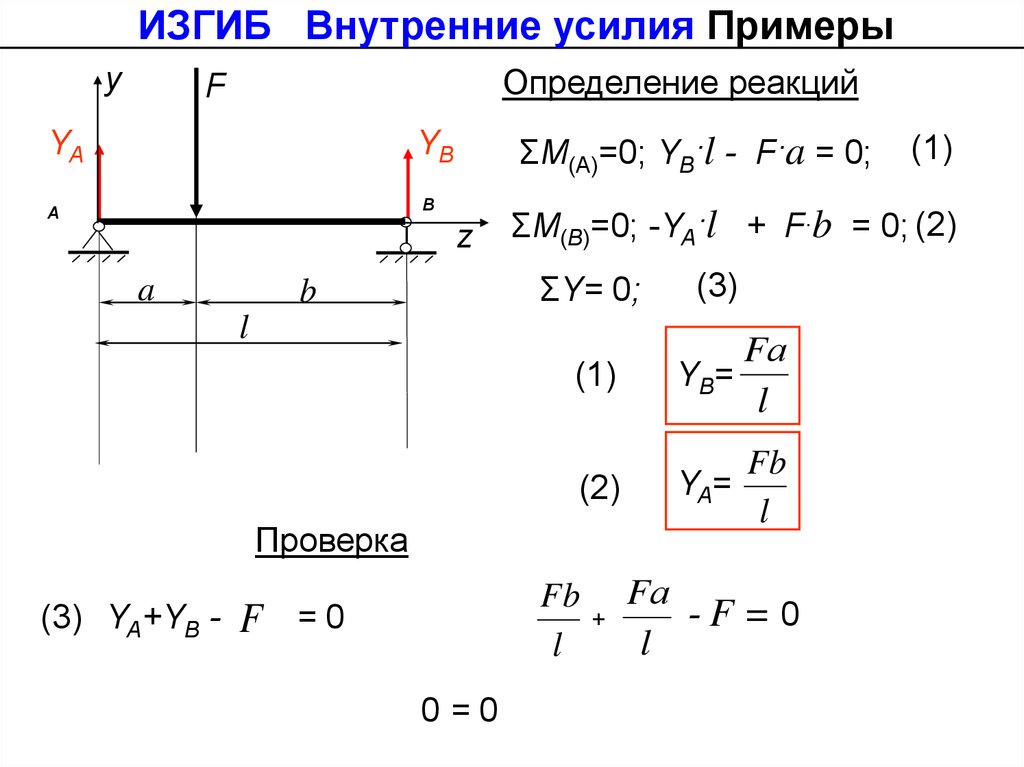
ИЗГИБ Внутренние усилия Примерыy
Определение реакций
F
YA
YB
ΣМ(А)=0; YB·l - F·a = 0;
B
A
z
a
ΣМ(B)=0; -YA·l + F·b = 0; (2)
ΣY= 0;
b
l
(1)
(2)
Fb
YA=
l
Fb
l
F =0
0=0
(3)
Fа
YB=
l
Проверка
(3) YA+YB -
(1)
+
Fа
-F=0
l
23.
ИЗГИБ Внутренние усилия Примерыy
YA
F
2
1
A
z1
a
l
Fb
l
«Q»
Fab
l
«М»
b
z2
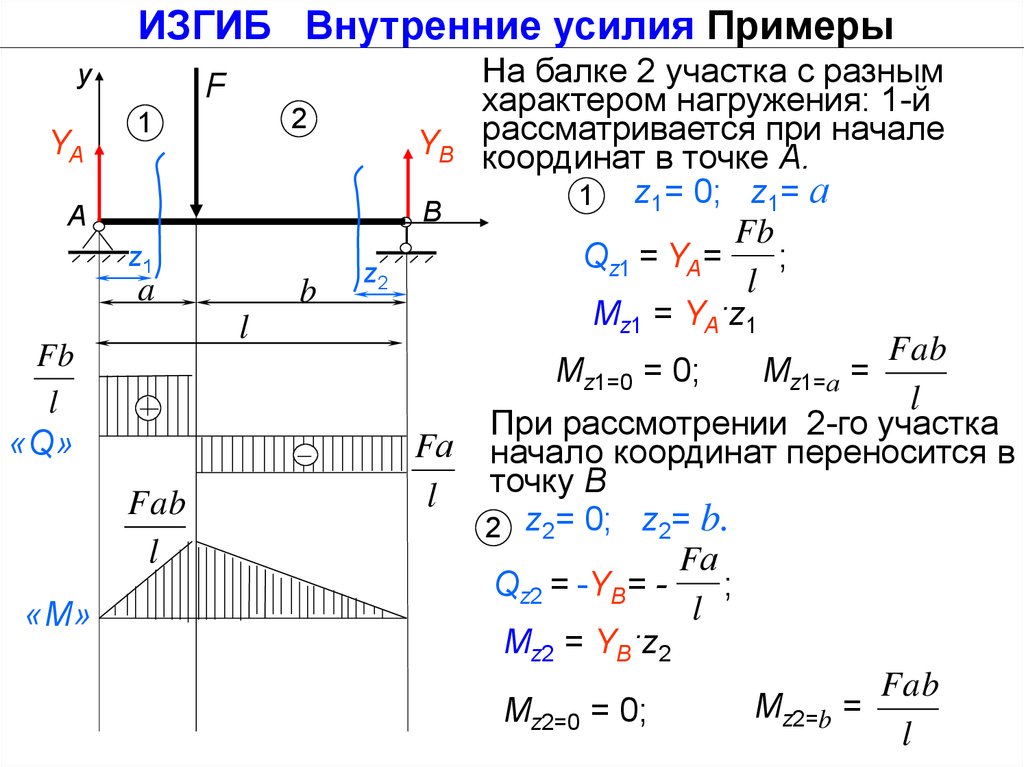
На балке 2 участка с разным
характером нагружения: 1-й
при начале
YB рассматривается
координат в точке А.
1 z1= 0; z1= а
B
Fb
Qz1 = YA=
;
l
Mz1 = YA·z1
Fab
Mz1=0 = 0;
Mz1=а =
l
При рассмотрении 2-го участка
Fа начало координат переносится в
точку В
l
2 z2= 0; z2= b.
Fа
Qz2 = -YВ= ;
l
Mz2 = YВ·z2
Fab
Mz2=b =
Mz2=0 = 0;
l
24.
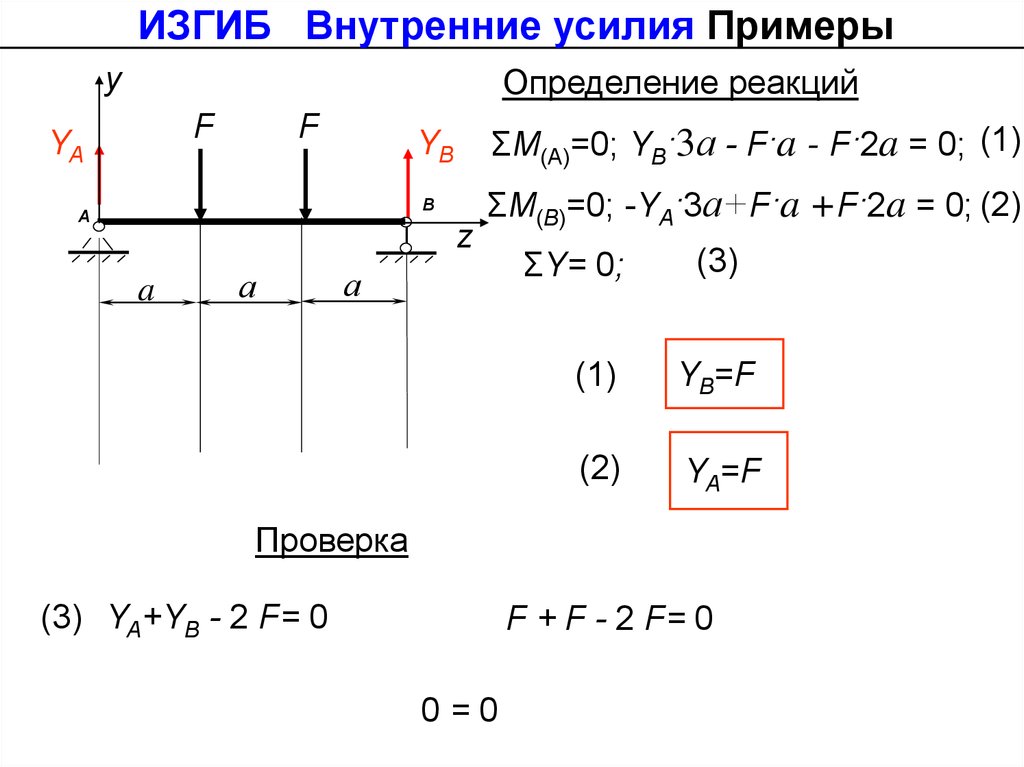
ИЗГИБ Внутренние усилия ПримерыОпределение реакций
y
F
YA
F
ΣМ(А)=0; YB·3а - F·a - F·2a = 0; (1)
YB
B
A
z
a
а
ΣМ(B)=0; -YА·3а+F·a +F·2a = 0; (2)
а
ΣY= 0;
(3)
(1)
YB=F
(2)
YA=F
Проверка
(3) YA+YB - 2 F= 0
F + F - 2 F= 0
0=0
25.
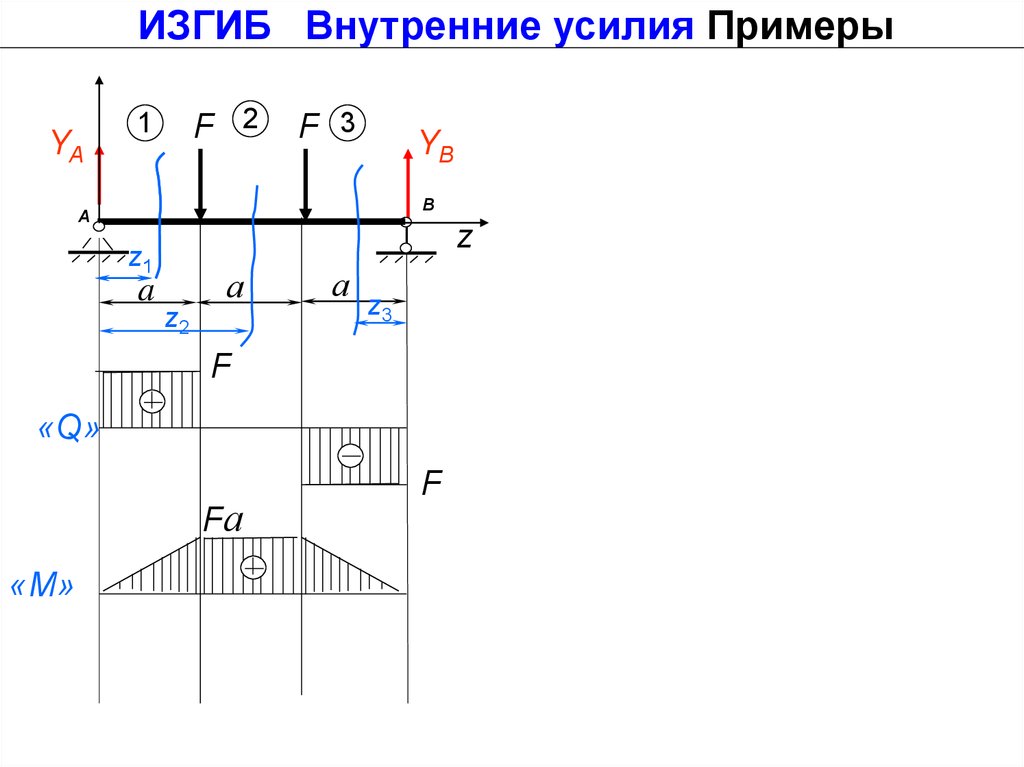
ИЗГИБ Внутренние усилия ПримерыYA
F 2
1
F 3
YB
B
A
z
z1
a
а
z2
а
z3
F
«Q»
Fа
«М»
F
26.
ИЗГИБ Внутренние усилия ПримерыF
YA
2
1
М
B
A
z1
М
l
«Q»
a
b
l
Ма
l
Мb
l
z2 Y
B
27.
ИЗГИБ Внутренние усилияКонтрольные правила для построения эпюр
1.На концевых шарнирных опорах поперечная
сила Qz равна реакциям, а Мz равны нулю, если
на опорах не приложены пары с моментами М.
2. На участках балки, где отсутствует распределенная
нагрузка, поперечная сила постоянна, а изгибающий
момент изменяется по линейному закону.
3. На участках, где приложена равномерно распределенная нагрузка, эпюра Qz изменяется по закону
прямой наклонной линии, а эпюра Мz - по закону
квадратичной параболы. В том сечении, где эпюра
Qz пересекается с осевой линией, на эпюре Мz
наблюдается экстремальное значение момента
(вершина параболы)
28.
ИЗГИБ Внутренние усилия4. В тех сечениях, где приложены сосредоточенные
силы (включая реакции), на эпюре Qz наблюдаются
скачки (перепады) на величину этих сил, а на эпюре
Мz - переломы смежных линий.
5. В тех сечениях, где приложены пары с моментами
М, на эпюре Мz наблюдаются скачки на величину этих
моментов.
6. На свободном конце консольной балки поперечная
сила Qz равна нулю, если в этом месте не приложена
сосредоточенная сила; и изгибающий момент Мz
равен нулю, если в этом месте не приложена пара с
моментом М
7. В жесткой заделке консольной балки Qz равна
реакции, а изгибающий момент Мz равен моменту
заделки.
29.
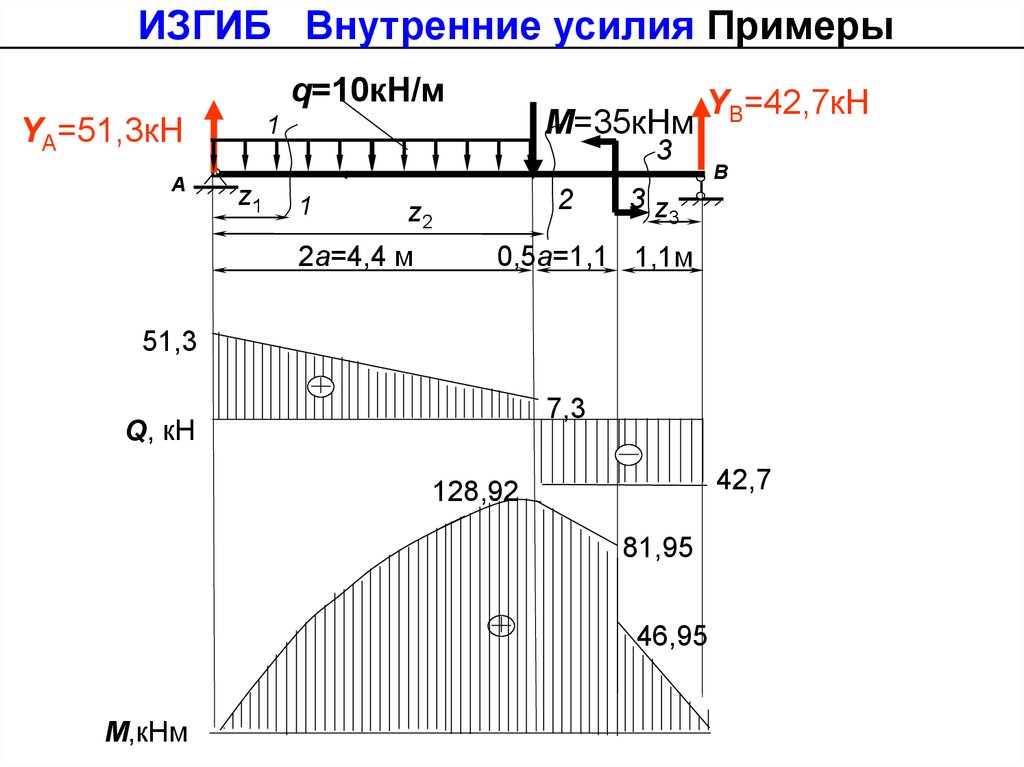
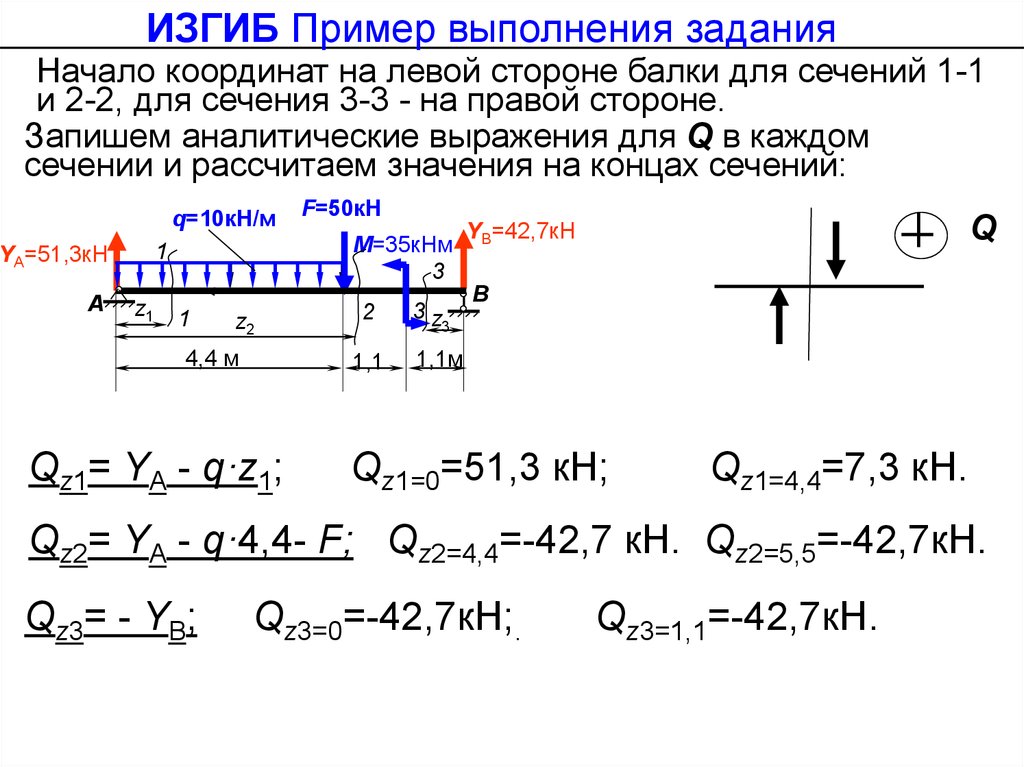
ИЗГИБ Внутренние усилия ПримерыНачало координат на левой стороне балки для сечений 1-1
и 2-2, для сечения 3-3 - на правой стороне.
Запишем аналитические выражения для Q в каждом
сечении и рассчитаем значения на концах сечений:
Qz1= YА - q·z1;
Qz1=0=51,3 кН;
Qz1=4,4=7,3 кН.
Qz2= YА - q·4,4- F Qz2=4,4=-42,7 кН.
Qz2=5,5=-42,7кН.
Qz3= - YВ; Qz3=0=-42,7кН.
Qz3=1,1=-42,7кН
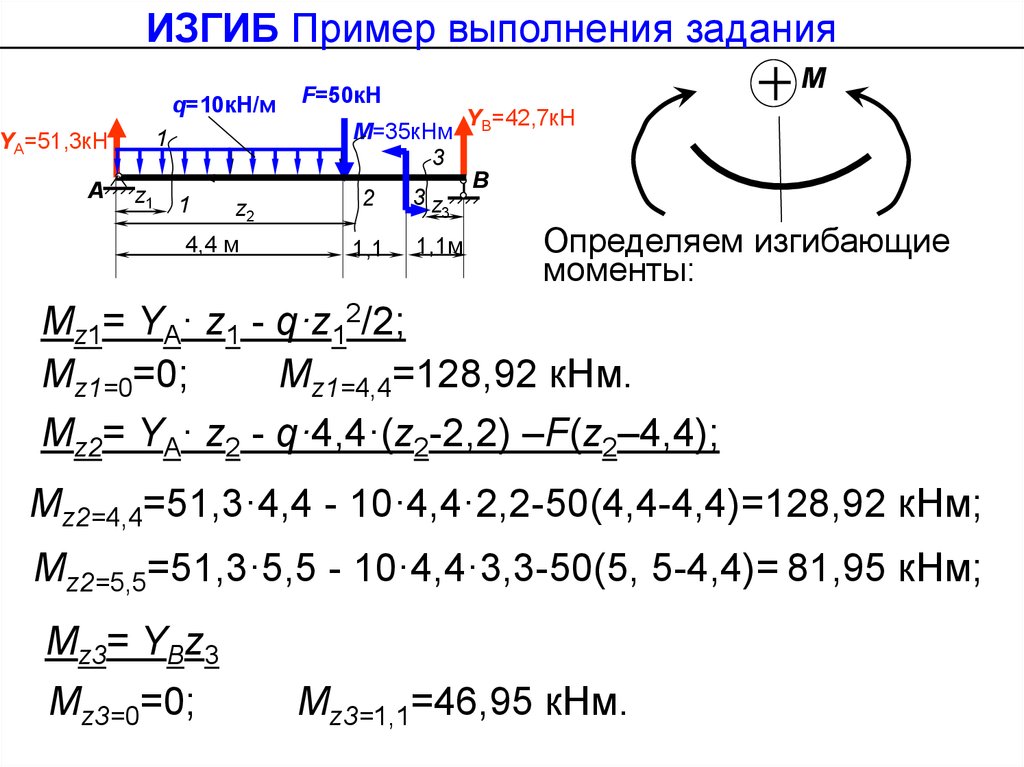
Определяем изгибающие моменты:
Mz1= YА· z1 - q·z12/2;
Mz1=0=0;
Mz1=4,4=128,92 кНм.
Mz2= YА· z2 - q·4,4·(z2-2,2) –F(z2–4,4); Mz2=4,4=128,92 кНм;
Mz2=5,5=81,95 кНм;
Mz3= YВz3;
Mz3=0=0;
Mz3=1,1=46,95 кНм.
Строим по полученным данным эпюру поперечных сил Q и
изгибающих моментов M. Выбираем масштаб и откладываем положительные значения ординат эпюр от нулевой
линии вверх, а отрицательные - вниз.
Опасное сечение - сечение с изгибающим моментом,
равным 128,92 кНм.
30.
ИЗГИБ Внутренние усилия Примерыq=10кН/м
YА=51,3кН
А
М=35кНм
1
YВ=42,7кН
3
z1
1
2
z2
2а=4,4 м
В
3z
3
0,5а=1,1 1,1м
51,3
7,3
Q, кН
42,7
128,92
81,95
46,95
М,кНм
31.
ИЗГИБ Определение напряжений и деформаций1
2
a
c
Me
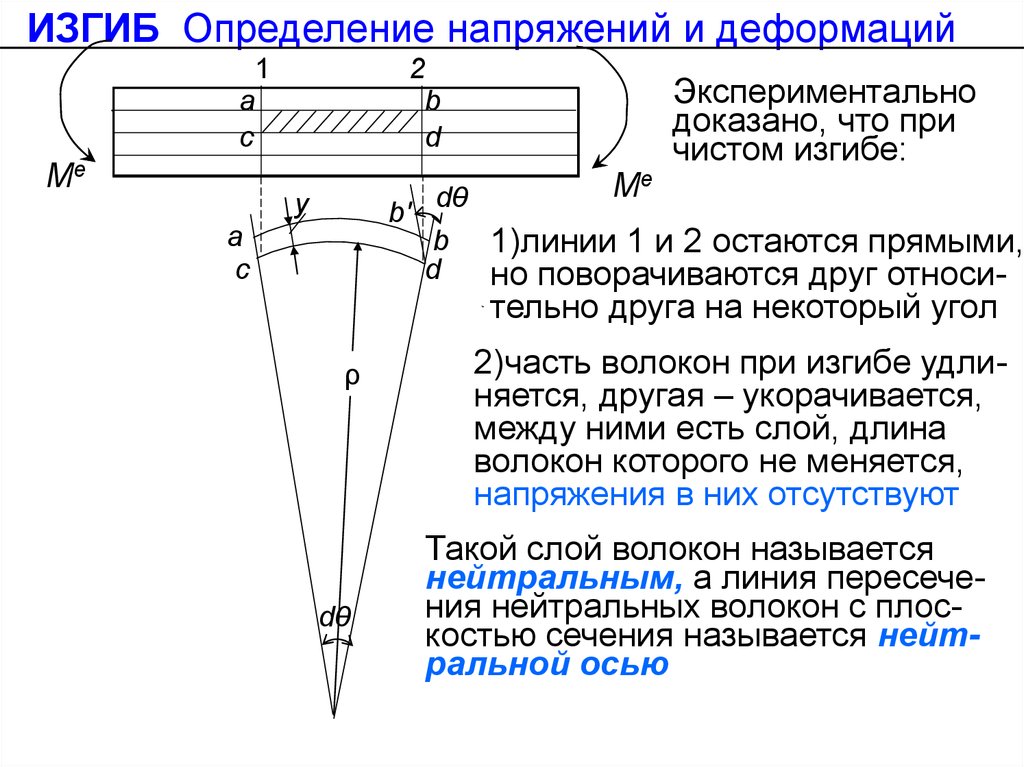
Экспериментально
доказано, что при
чистом изгибе:
b
d
y
b'
a
c
dθ
b
d
ρ
dθ
Me
1)линии 1 и 2 остаются прямыми,
но поворачиваются друг относительно друга на некоторый угол
2)часть волокон при изгибе удлиняется, другая – укорачивается,
между ними есть слой, длина
волокон которого не меняется,
напряжения в них отсутствуют
Такой слой волокон называется
нейтральным, а линия пересечения нейтральных волокон с плоскостью сечения называется нейтральной осью
32.
ИЗГИБ Определение напряжений и деформацийy
a
c
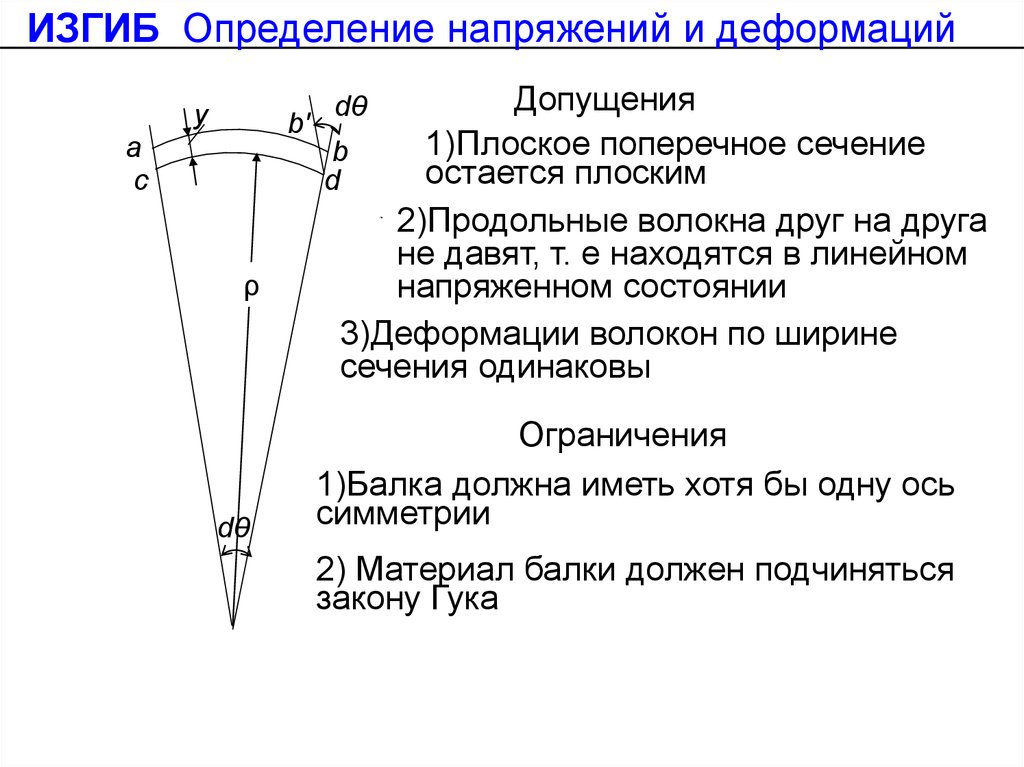
Допущения
b'
1)Плоское поперечное сечение
b
остается плоским
d
2)Продольные волокна друг на друга
не давят, т. е находятся в линейном
ρ
напряженном состоянии
3)Деформации волокон по ширине
сечения одинаковы
dθ
dθ
Ограничения
1)Балка должна иметь хотя бы одну ось
симметрии
2) Материал балки должен подчиняться
закону Гука
33.
ИЗГИБ Определение напряжений и деформацийa
y
b' dθ
b
d
c
ρ
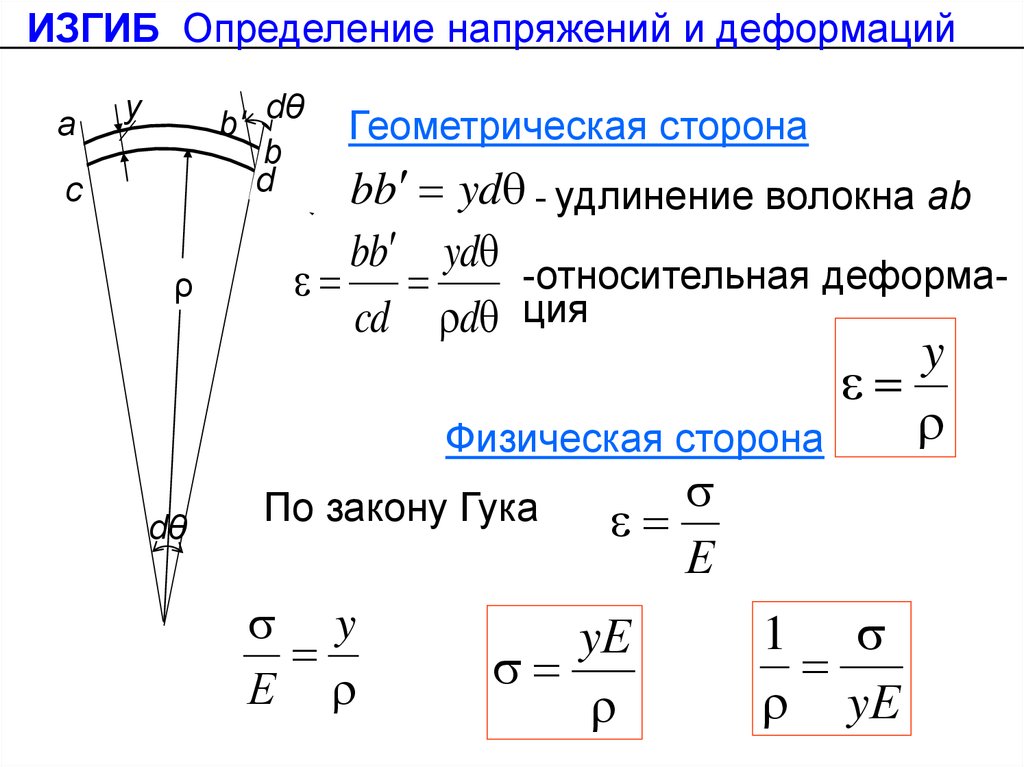
Геометрическая сторона
bb yd - удлинение волокна ab
bb yd -относительная деформа
cd d ция
Физическая сторона
dθ
По закону Гука
y
Е
y
Е
yЕ
1
yЕ
34.
ИЗГИБ Определение напряжений и деформацийСтатическая сторона
Ме
y
Ме
1
σdA
x
z
1
σdA – элементарная продольная сила
ΣFkx=0
ΣMx=Me-
ΣFky=0
ΣMy=-
ΣFkz= dA
А
0
ΣMz=0
dAy 0
А
dAx 0
А
35.
ИЗГИБ Определение напряжений и деформацийПодставляя значение σ в уравнения статики и преобразуя их,
получаем следующие выводы
1)Нейтральная ось проходит через центр сечения
2)Нейтральная ось является главной осью инерции и
перпендикулярна силовой плоскости
3)Нормальные напряжения определяются по формуле
M
y
Ix
или
M
Wx
3)Касательные напряжения определяются по формуле
Журавского
отс
QS x
I xb
36.
ИЗГИБ Пример выполнения заданияРасчет балки на прочность и жесткость
Для расчетной схемы балки необходимо:
1. Построить по длине балки эпюры изгибающих моментов и
поперечных сил.
2.Подобрать поперечное сечение балки двутаврового
профиля, материал Cталь 3 при σadm = 160 МПa,
τadm = 96 МПа.
3. Подобрать прямоугольное поперечное сечение балки,
материал – дерево, σadm = 10 МПa.
4. Провести проверку стальной балки на жёсткость,
определив по методу начальных параметров величину
прогибов балки в характерных сечениях. Принять
уadm=(1/100) l.
37.
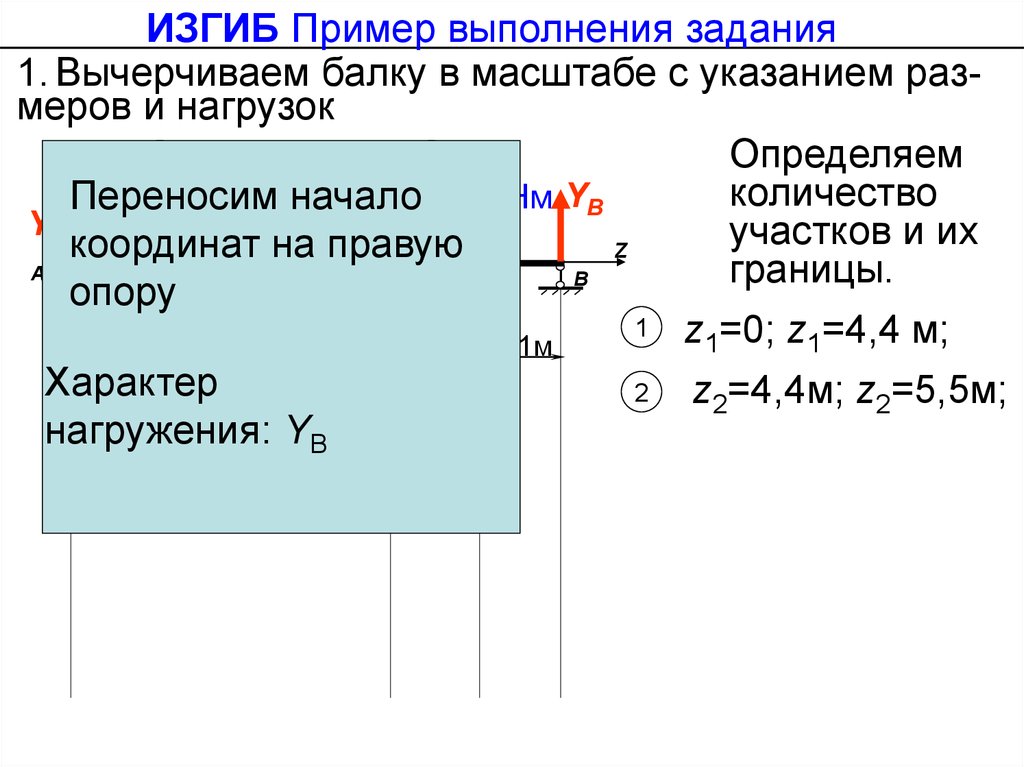
ИЗГИБ Пример выполнения задания1. Вычерчиваем балку в масштабе с указанием размеров и нагрузок
2.Определяем реакции опор
из уравнений равновесия
F=50кН
q=10кН/м
1
YА=51,3кН
А
М=35кНм YВ=42,7кН
3
z1
1
z2
4,4 м
2
1,1
В
3z
3
1,1м
ΣM(A)=0; M- q·4,4·2,2 - F·4,4 + YВ·6,6 = 0;
YВ =(- M + q·4,4·2,2 + F·4,4)/6,6 = 42,7 кН.
ΣM(В)=0; M + q ·4,4·4,4 + F·2,2 – YА·6,6 = 0;
YА =(M + q ·4,4·4,4 + F·2,2 )/6,6 = 51,3 кН.
Проверка
ΣY =0; YА + YВ - q·4,4 - F =0;
51,3 + 42,7 – 44 – 50 =0 0=0.
38.
ИЗГИБ Пример выполнения заданияу
YА
А
F=50кН
1Закрыта
отброшенная
q=10кН/м
часть
М=35кНм YВ
Характер нагружения: В
YA4,4имq
1,1м 1,1м
z
3.Определяем
количество
участков и их
границы.
39.
ИЗГИБ Пример выполнения задания1. Вычерчиваем балку в масштабе с указанием размеров и нагрузок
F=50кН
2.Определяем2
1
у
q=10кН/м
количество
YВ
М=35кНм
Изменился
YА
участков и их
характерz
А
границы.
В
нагружения,
1 z =0; z =4,4 м;
1
1
4,4 м
1,1м добавилась
1,1м
сила
40.
ИЗГИБ Пример выполнения задания1. Вычерчиваем балку в масштабе с указанием размеров и нагрузок
F=50кН 2
Определяем
1
у
q=10кН/м
количество
М=35кНм YВ
YА
участков и их
z
А
границы.
В
4,4 м
1,1м
1,1м
1
2
z1=0; z1=4,4 м;
z2=4,4м; z2=5,5м;
41.
ИЗГИБ Пример выполнения задания1. Вычерчиваем балку в масштабе с указанием размеров и нагрузок
F=50кН 2
Определяем
1
у
q=10кН/м
количество
Переносим
началоМ=35кНм YВ
YА
участков и их
координат на правую
z
А
границы.
В
опору
1 z =0; z =4,4 м;
1
1
4,4 м
1,1м 1,1м
Характер
2
z2=4,4м; z2=5,5м;
нагружения: YB
42.
33
3
F=50кН
q=10кН/м
М=35кНм
3 YВ
1
у
YА
А
z1
1
z2
3
z3
2
4,4 м
1,1м
z
В
1,1м
3
z3=0; z3=1.1м;
Проводим сечения
43.
ИЗГИБ Пример выполнения заданияНачало координат на левой стороне балки для сечений 1-1
и 2-2, для сечения 3-3 - на правой стороне.
Запишем аналитические выражения для Q в каждом
сечении и рассчитаем значения на концах сечений:
q=10кН/м
А
М=35кНм
3
1
YА=51,3кН
z1
F=50кН
1
z2
4,4 м
2
1,1
Qz1= YА - q·z1;
3z
Q
YВ=42,7кН
В
3
1,1м
Qz1=0=51,3 кН;
Qz1=4,4=7,3 кН.
Qz2= YА - q·4,4- F; Qz2=4,4=-42,7 кН. Qz2=5,5=-42,7кН.
Qz3= - YВ;
Qz3=0=-42,7кН;.
Qz3=1,1=-42,7кН.
44.
ИЗГИБ Пример выполнения заданияq=10кН/м
YА=51,3кН
А
М=35кНм
3
1
z1
M
F=50кН
1
z2
4,4 м
2
1,1
3z
YВ=42,7кН
В
3
1,1м
Определяем изгибающие
моменты:
Mz1= YА· z1 - q·z12/2;
Mz1=0=0;
Mz1=4,4=128,92 кНм.
Mz2= YА· z2 - q·4,4·(z2-2,2) –F(z2–4,4);
Mz2=4,4=51,3·4,4 - 10·4,4·2,2-50(4,4-4,4)=128,92 кНм;
Mz2=5,5=51,3·5,5 - 10·4,4·3,3-50(5, 5-4,4)= 81,95 кНм;
Mz3= YВz3
Mz3=0=0;
Mz3=1,1=46,95 кНм.
45.
ИЗГИБ Внутренние усилия ПримерыYВ=42,7кН
М=35кНм
YА=51,3кН q=10кН/м
1
3
А
z1
1
2
z2
2а=4,4 м
3z
3
0,5а=1,1 1,1м
51,3
7,3
Q, кН
Выбираем масштаб
и откладываем
положительные
значения ординат
эпюр от нулевой
линии вверх, а
отрицательные вниз.
42,7
128,92
81,95
46,95
М,кНм
В
Опасное сечение сечение с изгибающим моментом,
равным 128,92 кНм.
46.
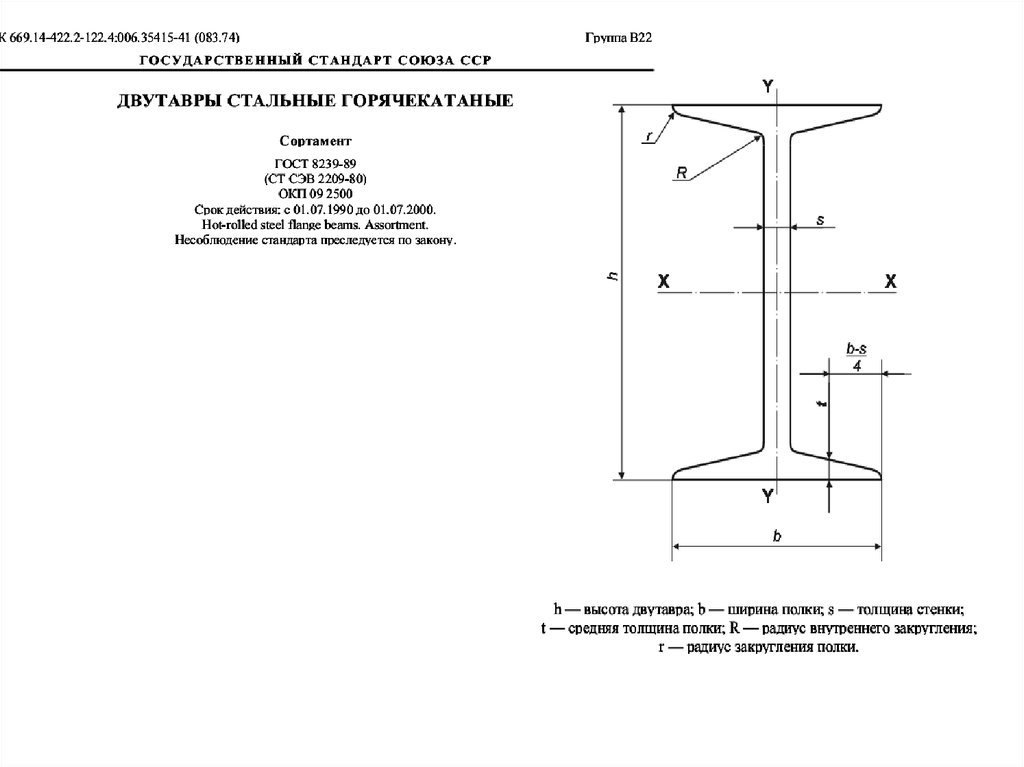
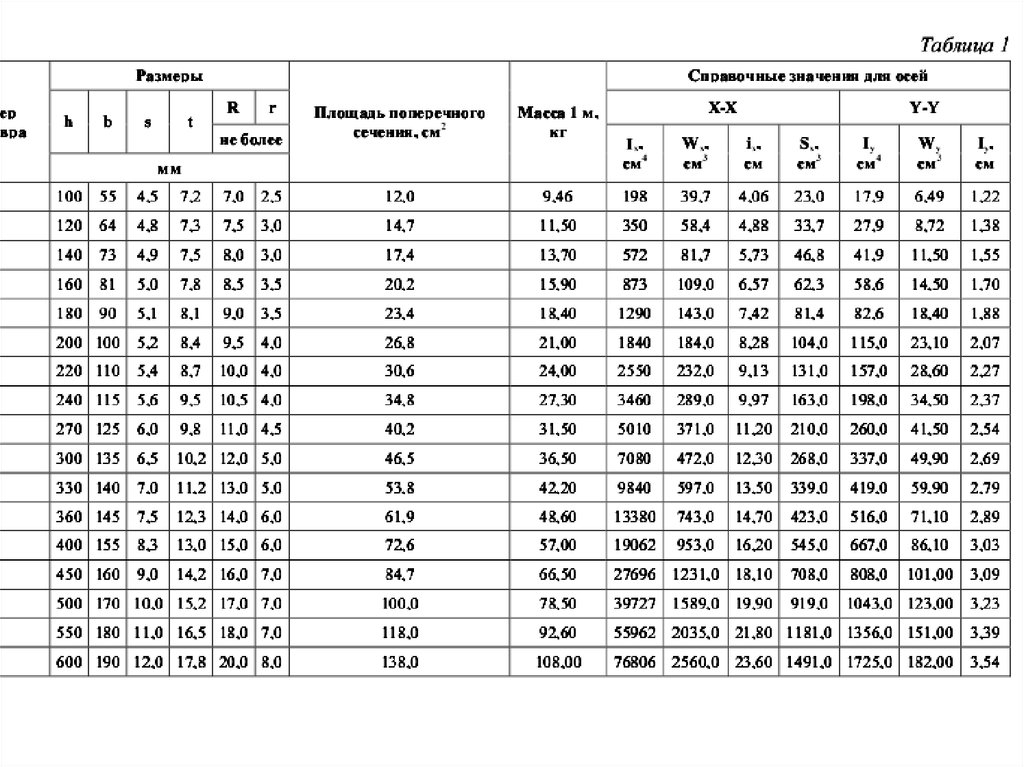
ИЗГИБ Пример выполнения заданияПодбор сечения двутаврового профиля выполняем
из условия прочности при изгибе
откуда
Mx
adm
Wн.о.
Wн.о.
Mx
adm
где Wн.о. – момент сопротивления относительно
нейтральной оси, которая в сечении балки совпадает
с осью х
Wн.о.
128 ,92 10 3
8,05 10 4 м3 =805 см3
160
47.
48.
49.
ИЗГИБ Пример выполнения задания50.
ИЗГИБ Пример выполнения заданияа) Проверка по рабочим нормальным напряжениям:
M x 128 ,92 10 3
136 МПа adm =160 МПа,
6
Wн.о.
947 10
т. е. условие прочности выполняется.
51.
ИЗГИБ Пример выполнения заданияб) Проверка
напряжениям:
по
максимальным
касательным
отc
Qmax S н.о.
I н.о.b
Sx- статический момент отсеченной (верхней части)
относительно оси х в сечении;
Ix - момент инерции сечения,
b – толщина стенки, для двутавра b=d;
51,3 10 3 540 10 6
18,3 <96 МПа
8
3
18930 10 8 10
условие прочности по касательным напряжениям
также выполняется.
52.
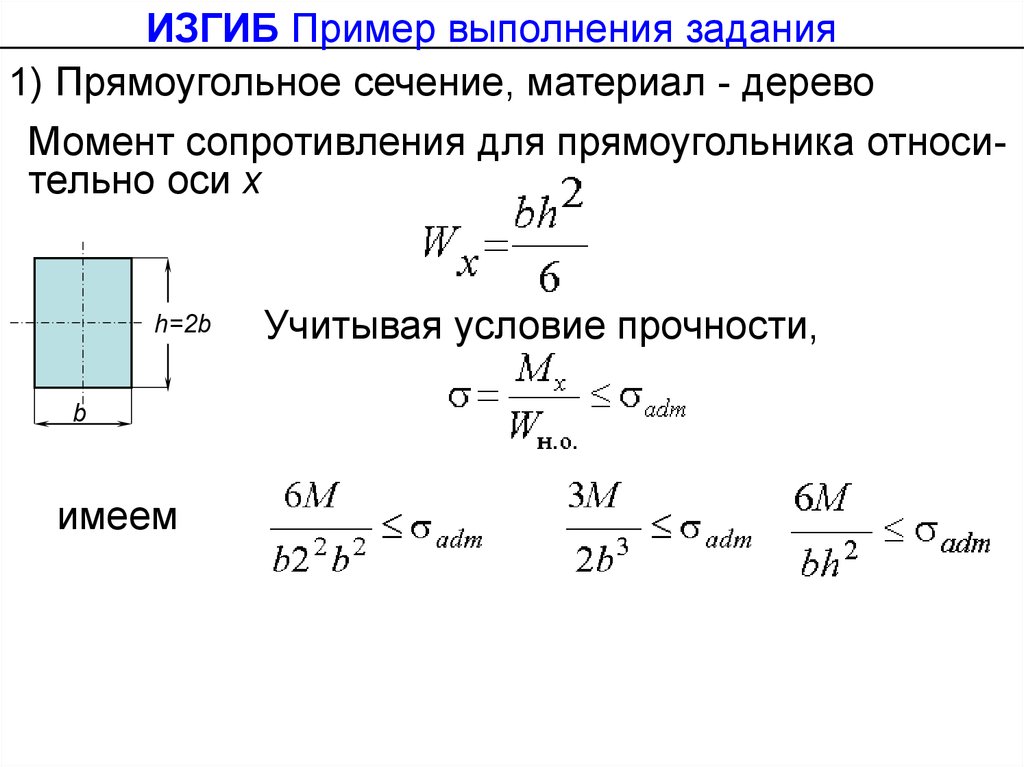
ИЗГИБ Пример выполнения задания1) Прямоугольное сечение, материал - дерево
Момент сопротивления для прямоугольника относительно оси х
h=2b
b
имеем
Учитывая условие прочности,
53.
ИЗГИБ Пример выполнения заданияb x h = 144 x 288 мм2
Деревянное сечение по расходу материала весьма
не экономично.
































 physics
physics








