Similar presentations:
Изгиб прямолинейного бруса
1.
ИЗГИБПРЯМОЛИНЕЙНОГО
БРУСА
Правила контроля эпюр
2.
аRB
R
A
а
b
RB
F
R
A
b
F
R
B
F
F
RA
RB
RA
RA
a
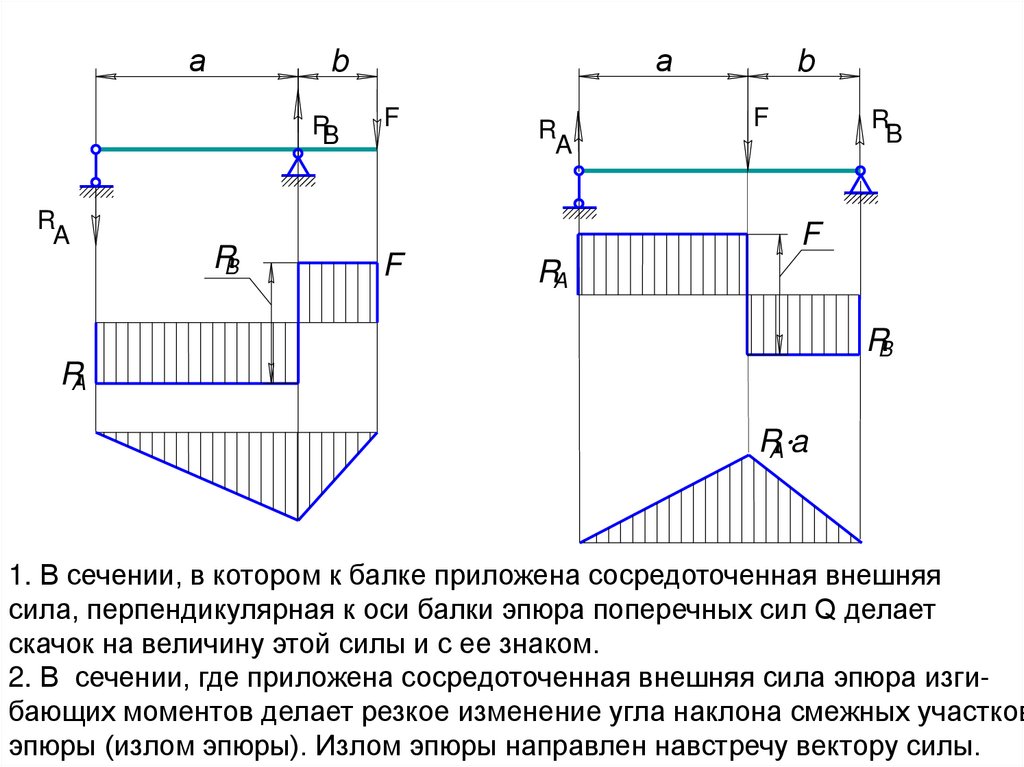
1. В сечении, в котором к балке приложена сосредоточенная внешняя
сила, перпендикулярная к оси балки эпюра поперечных сил Q делает
скачок на величину этой силы и с ее знаком.
2. В сечении, где приложена сосредоточенная внешняя сила эпюра изгибающих моментов делает резкое изменение угла наклона смежных участков
эпюры (излом эпюры). Излом эпюры направлен навстречу вектору силы.
3.
аb
RA
R
M
RA
B
R
B
RA
a
M
q
R
A
l
В
RB
2
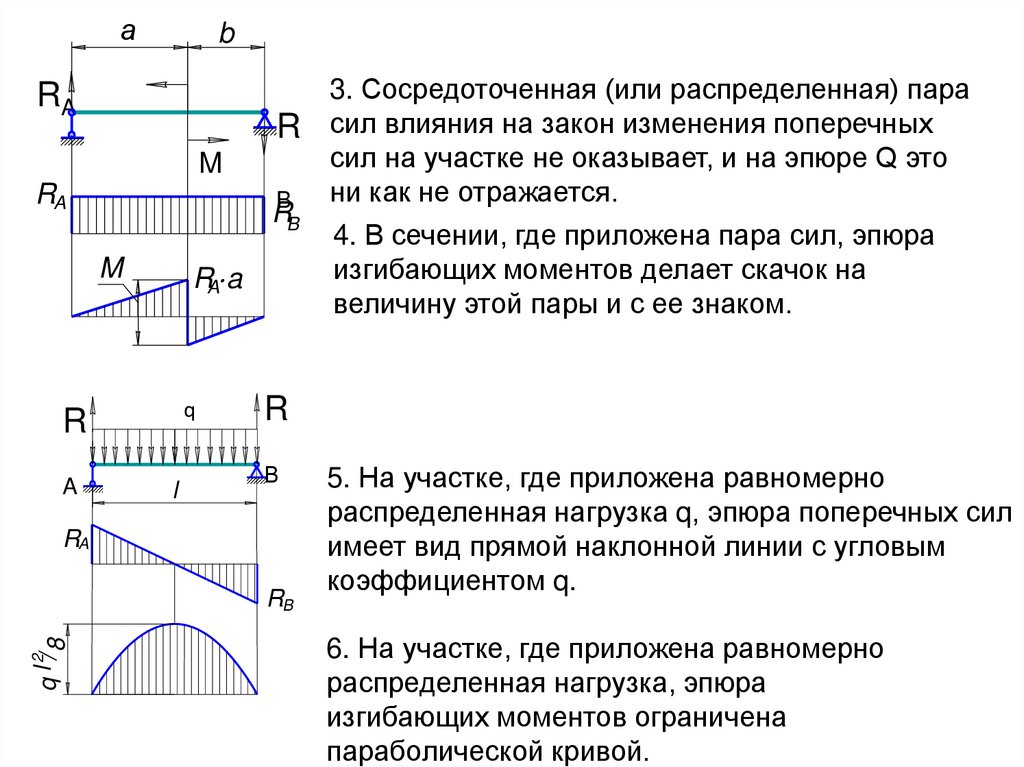
4. В сечении, где приложена пара сил, эпюра
изгибающих моментов делает скачок на
величину этой пары и с ее знаком.
R
RA
q l /8
3. Сосредоточенная (или распределенная) пара
сил влияния на закон изменения поперечных
сил на участке не оказывает, и на эпюре Q это
ни как не отражается.
5. На участке, где приложена равномерно
распределенная нагрузка q, эпюра поперечных сил
имеет вид прямой наклонной линии с угловым
коэффициентом q.
6. На участке, где приложена равномерно
распределенная нагрузка, эпюра
изгибающих моментов ограничена
параболической кривой.
4.
аRA
a
а
F
l
RA
F
a
F
F
RB
RB
RA
F
RA
RB
RB
RA
a
RA
a
RB
a
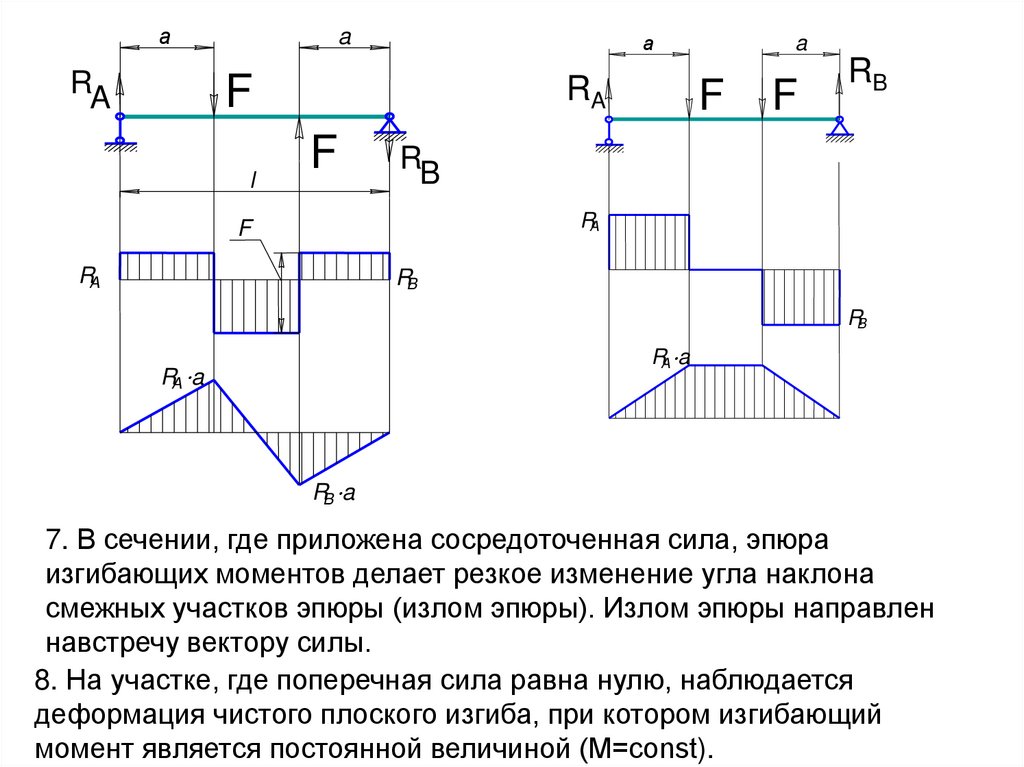
7. В сечении, где приложена сосредоточенная сила, эпюра
изгибающих моментов делает резкое изменение угла наклона
смежных участков эпюры (излом эпюры). Излом эпюры направлен
навстречу вектору силы.
8. На участке, где поперечная сила равна нулю, наблюдается
деформация чистого плоского изгиба, при котором изгибающий
момент является постоянной величиной (М=const).
5.
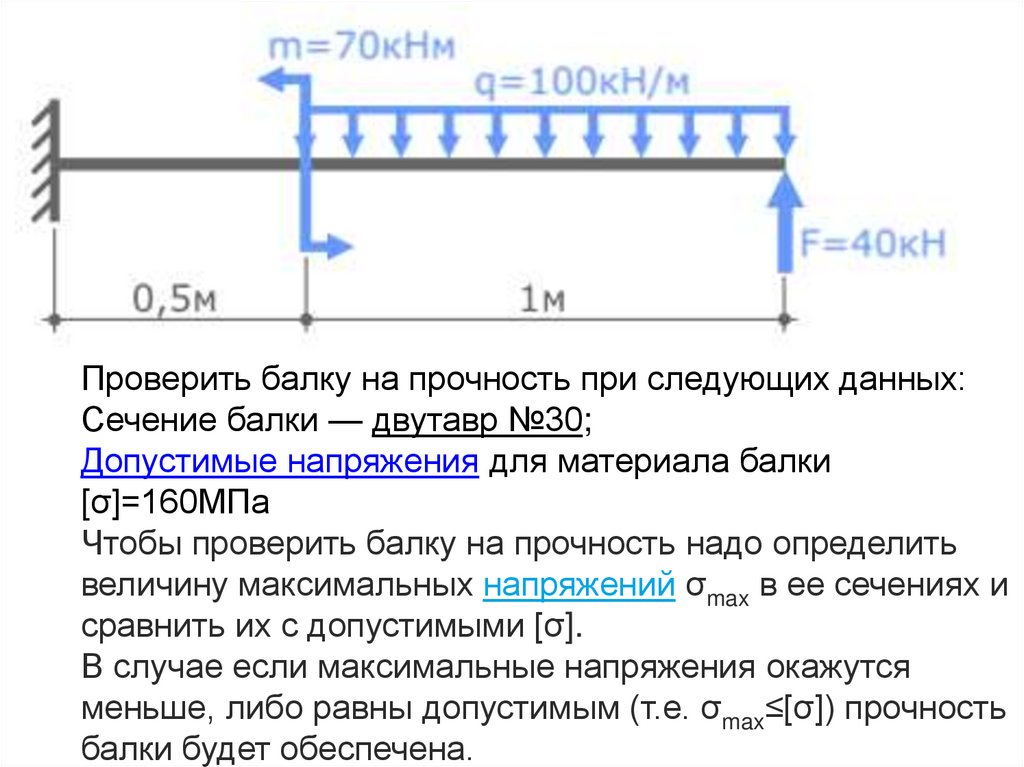
Проверить балку на прочность при следующих данных:Сечение балки — двутавр №30;
Допустимые напряжения для материала балки
[σ]=160МПа
Чтобы проверить балку на прочность надо определить
величину максимальных напряжений σmax в ее сечениях и
сравнить их с допустимыми [σ].
В случае если максимальные напряжения окажутся
меньше, либо равны допустимым (т.е. σmax≤[σ]) прочность
балки будет обеспечена.
6.
Если же найденные напряжения превысят величинудопустимых (т.е. σ >[σ]) значит балка не прочная.
Условие прочности при плоском поперечном изгибе:
max
Здесь:
M – внутренний изгибающий момент, W – осевой
момент сопротивления сечения балки.
У балки постоянного сечения, форма и размеры
сечения одинаковы по всей ее длине, следовательно,
W =const.
Тогда очевидно, что наибольшими напряжения
окажутся в сечении, где будет максимальный
изгибающий момент M (по эпюре).
x
x
x
Для построения эпюр сначала надо определить
опорные реакции.
7.
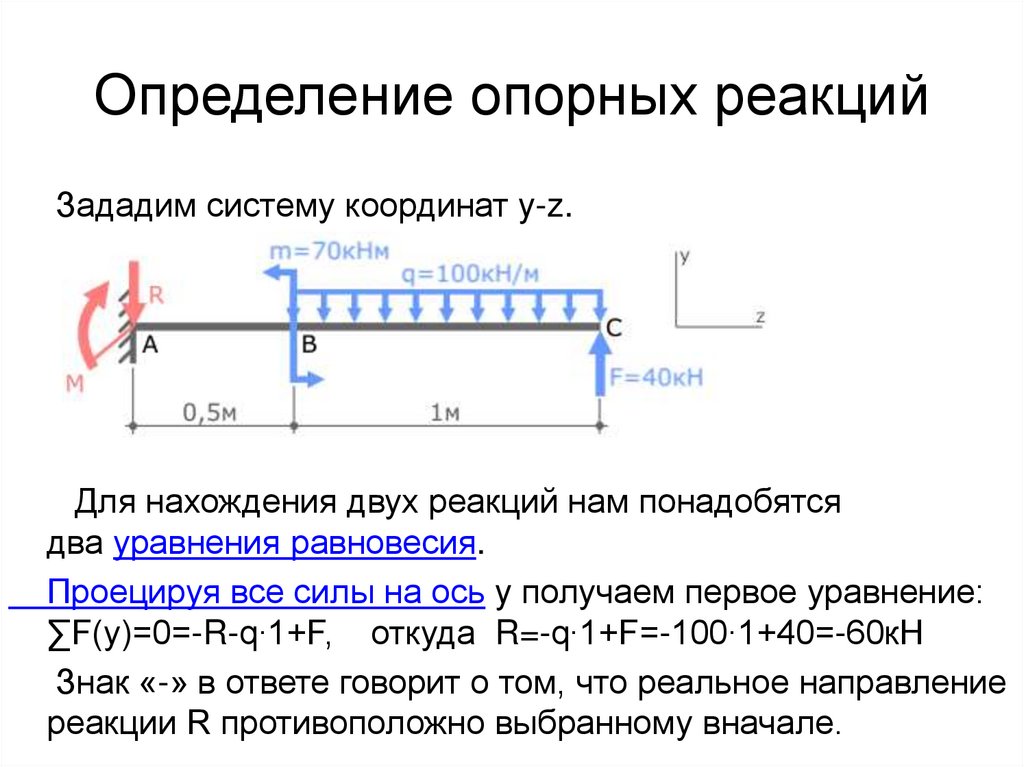
Определение опорных реакцийЗададим систему координат y-z.
Для нахождения двух реакций нам понадобятся
два уравнения равновесия.
Проецируя все силы на ось y получаем первое уравнение:
∑F(y)=0=-R-q∙1+F, откуда R=-q∙1+F=-100∙1+40=-60кН
Знак «-» в ответе говорит о том, что реальное направление
реакции R противоположно выбранному вначале.
8.
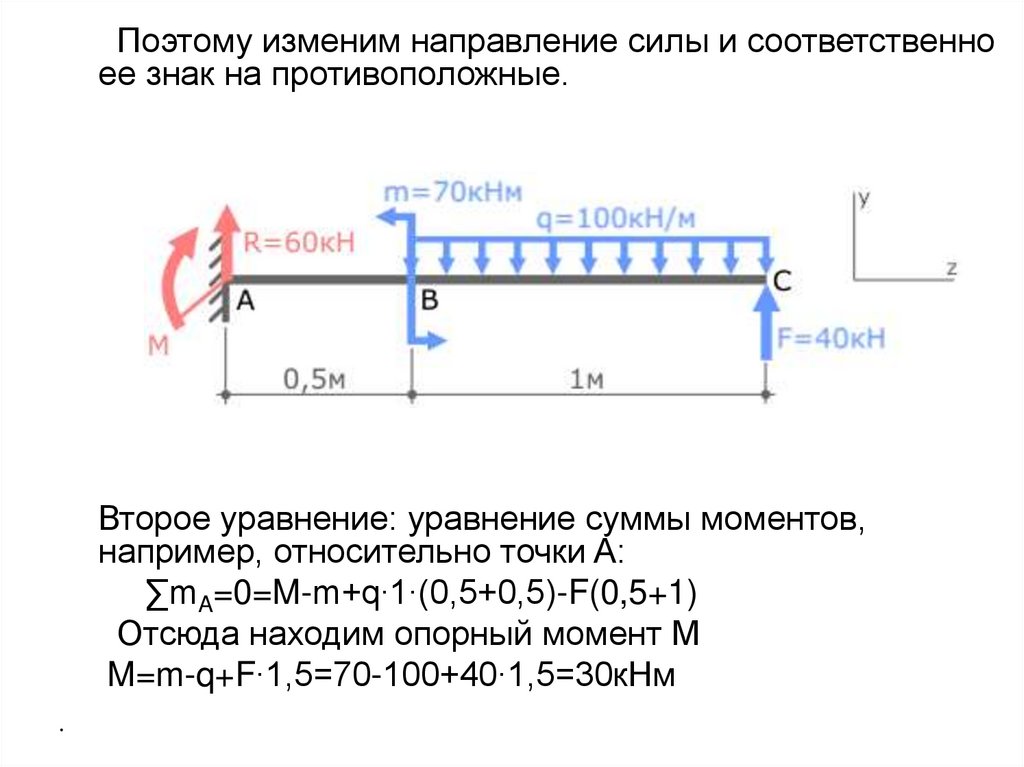
Поэтому изменим направление силы и соответственноее знак на противоположные.
Второе уравнение: уравнение суммы моментов,
например, относительно точки A:
∑mA=0=M-m+q∙1∙(0,5+0,5)-F(0,5+1)
Отсюда находим опорный момент M
M=m-q+F∙1,5=70-100+40∙1,5=30кНм
9.
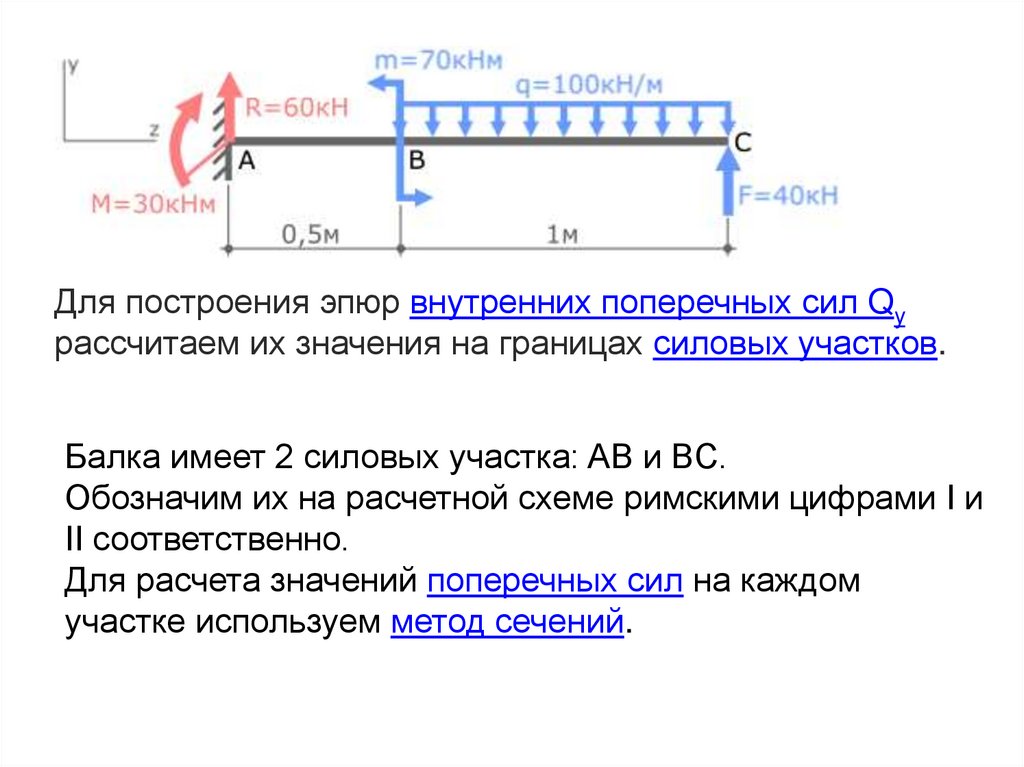
Для построения эпюр внутренних поперечных сил Qyрассчитаем их значения на границах силовых участков.
Балка имеет 2 силовых участка: AB и BC.
Обозначим их на расчетной схеме римскими цифрами I и
II соответственно.
Для расчета значений поперечных сил на каждом
участке используем метод сечений.
10.
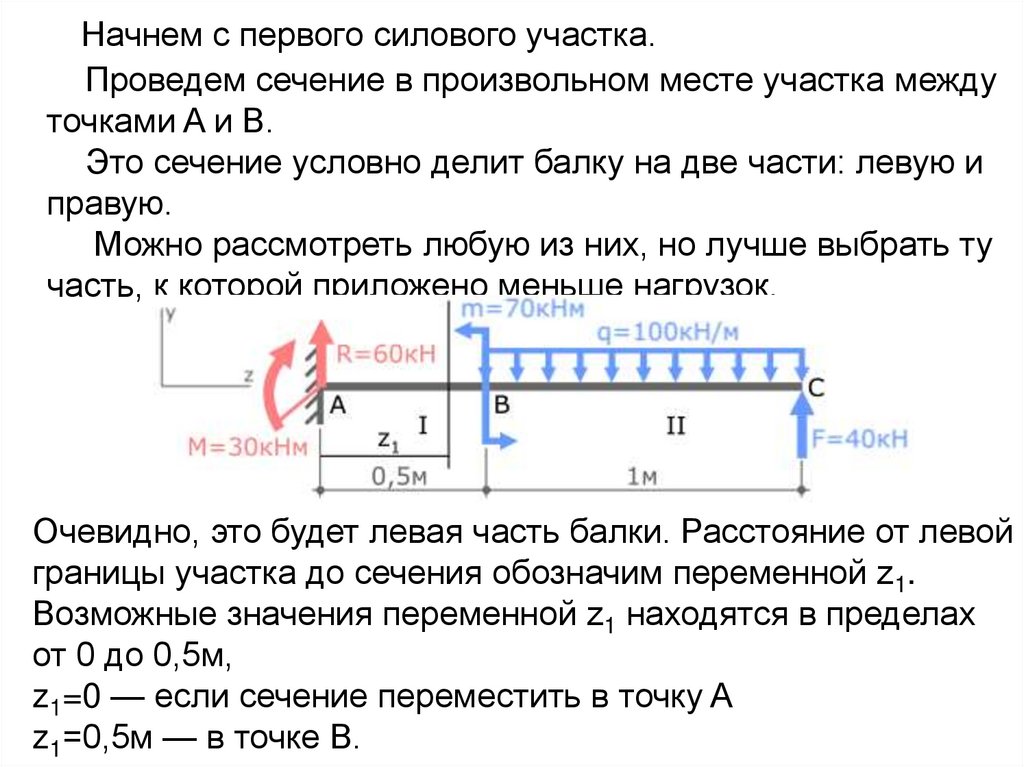
Начнем с первого силового участка.Проведем сечение в произвольном месте участка между
точками A и B.
Это сечение условно делит балку на две части: левую и
правую.
Можно рассмотреть любую из них, но лучше выбрать ту
часть, к которой приложено меньше нагрузок.
Очевидно, это будет левая часть балки. Расстояние от левой
границы участка до сечения обозначим переменной z1.
Возможные значения переменной z1 находятся в пределах
от 0 до 0,5м,
z1=0 — если сечение переместить в точку A
z1=0,5м — в точке B.
11.
Отбросим правую часть балки.Запишем имеющиеся данные:
I с.у.: 0≤z1≤0,5м
Поперечная сила в указанном сечении равна сумме всех
вертикальных внешних сил, приложенных к
рассматриваемой части балки.
К рассматриваемой левой части балки приложена только
одна сила — опорная реакция R.
По правилу знаков, если сила стремится повернуть
рассматриваемую часть балки относительно сечения по
ходу часовой стрелки, она записывается положительной.
QyI=ΣFi=R=60кН
В выражении отсутствует переменная z1. Это указывает на
то, что поперечная сила QyI одинакова для всех сечений I
силового участка.
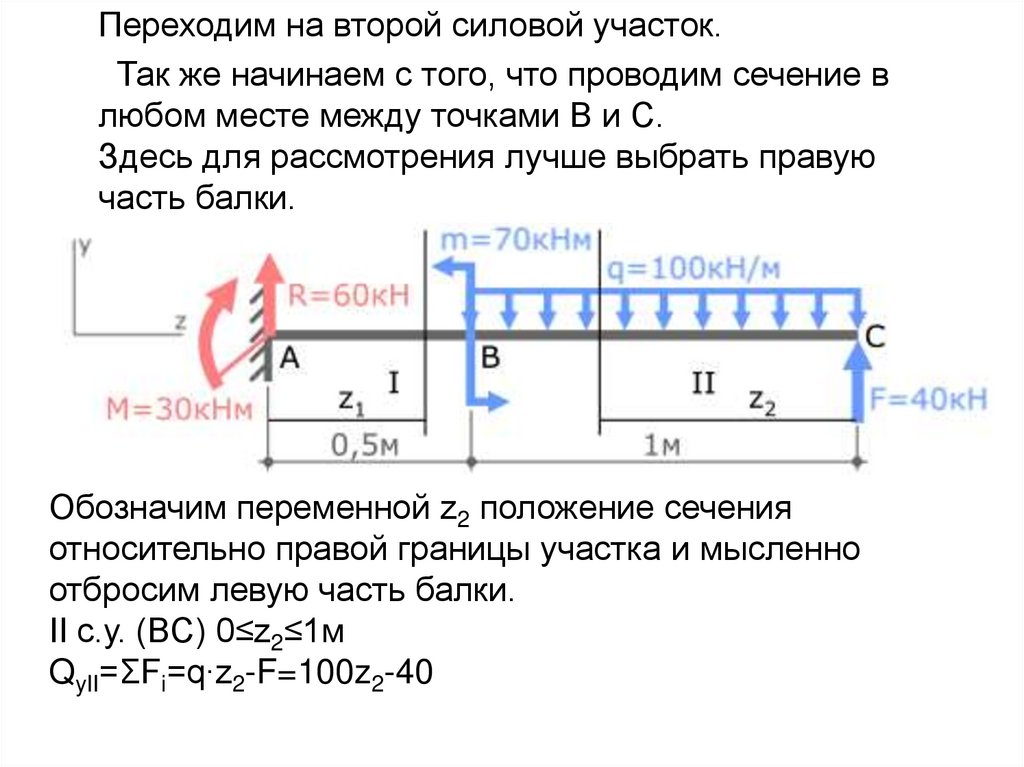
12.
Переходим на второй силовой участок.Так же начинаем с того, что проводим сечение в
любом месте между точками B и C.
Здесь для рассмотрения лучше выбрать правую
часть балки.
Обозначим переменной z2 положение сечения
относительно правой границы участка и мысленно
отбросим левую часть балки.
II с.у. (BC) 0≤z2≤1м
QyII=ΣFi=q∙z2-F=100z2-40
13.
Получено выражение, где имеется переменная Z2.Переменная имеет первую степень, поэтому ее графиком
будет прямая. Для её построения достаточно двух точек.
Этими точками будут значения Qy на границах II силового
участка, то есть при z2=0 и при z2=1м.
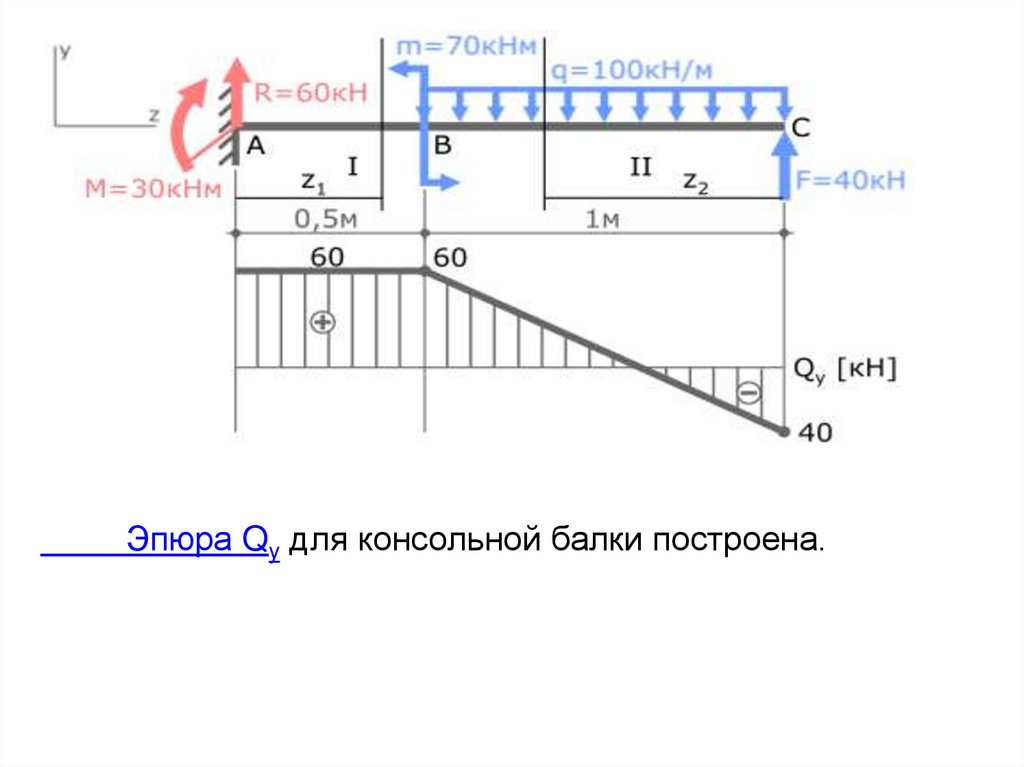
QyII(z2=0)=100∙0-40=-40кН
QyII(z2=1м)=100∙1-40=60кН
Удлиним линии границ силовых участков, начертим
базовую линию и укажем обозначение и размерность
эпюры. Обозначим полученные значения
соответствующими точками на эпюре и соединим их.
14.
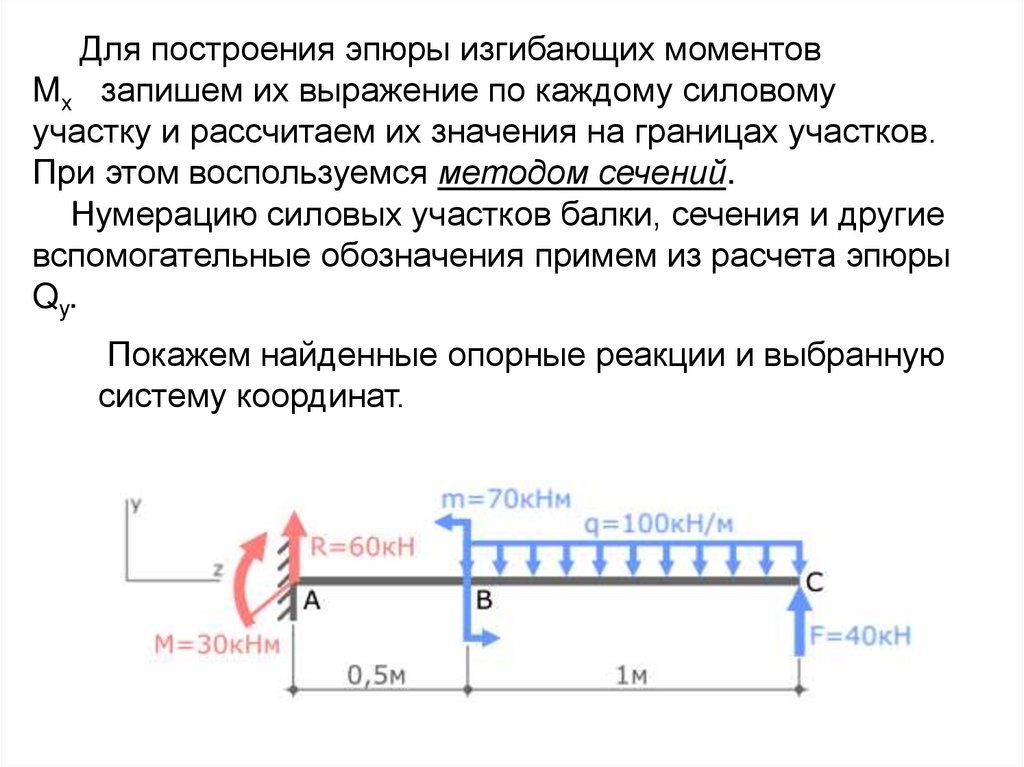
Эпюра Qy для консольной балки построена.15.
Для построения эпюры изгибающих моментовMx запишем их выражение по каждому силовому
участку и рассчитаем их значения на границах участков.
При этом воспользуемся методом сечений.
Нумерацию силовых участков балки, сечения и другие
вспомогательные обозначения примем из расчета эпюры
Qy.
Покажем найденные опорные реакции и выбранную
систему координат.
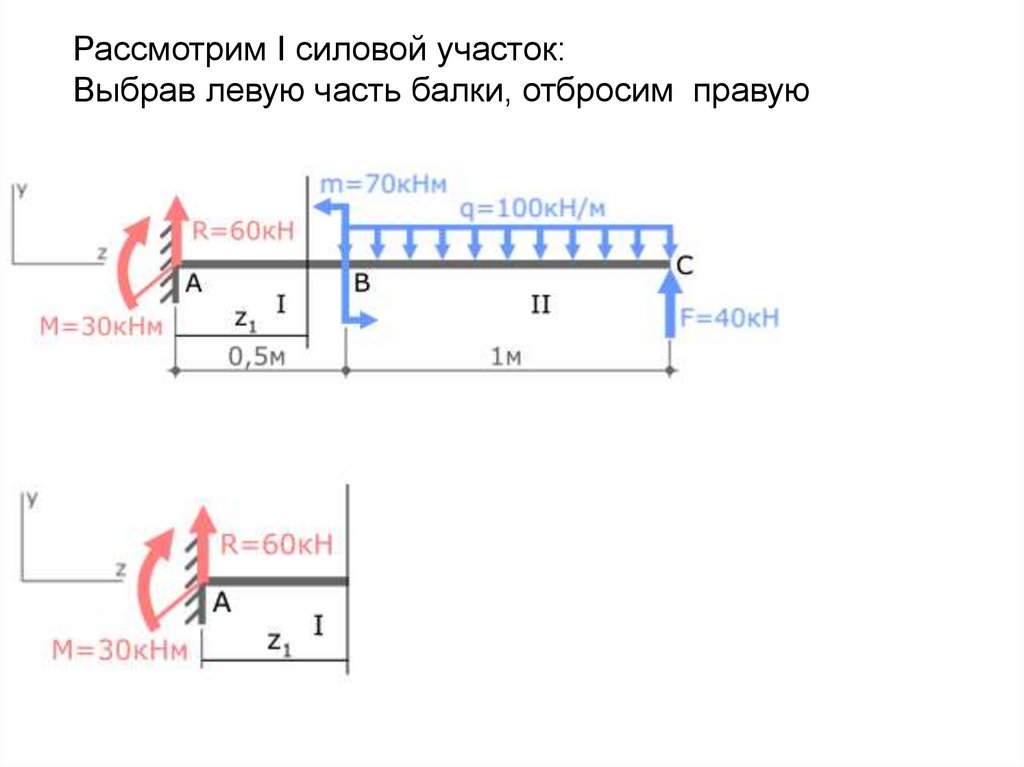
16.
Рассмотрим I силовой участок:Выбрав левую часть балки, отбросим правую
17.
I с.у. (AB) 0 ≤ z1≤ 0,5мВнутренний изгибающий момент в указанном
сечении равен сумме всех внешних моментов,
воздействующих на рассматриваемую часть
балки.
По правилу знаков момент, который
стремится сжать верхние слои балки,
принимается положительным, следовательно:
MxI=Σmi=M+R∙z1=30+60z1
В выражении переменная z1 в первой степени,
поэтому эпюра Mx на первом участке будет
иметь вид прямой линии.
18.
Рассчитаем значения MxI на границах участка, т.е. приz1=0 и при z1=0,5м
MxI (z1=0)=30кНм
MxI (z1=0,5м)=60кНм
Переходим на второй силовой участок: рассекаем
балку в произвольном месте участка и рассматриваем
её правую часть.
Эта часть балки изгибается силой F и распределенной
нагрузкой q.
19.
II с.у. (BC) 0 ≤ z2 ≤ 1м
MxII=Σmi= -q∙z2(z2/2)+F∙z2 = -50∙z22+40∙z2
Получено выражение с переменной z2 во второй степени,
значит, эпюра Mx на втором участке будет иметь вид
параболы.
Для построения параболы требуется как минимум три
точки. Этими точками будут значения Mx на границах и в
середине II силового участка, то есть при z2=0, z2=1м и
z2=0,5м.
MxII(z2=0)=0; MxII(z2=0,5м)=7,5кНм; MxII(z2=1м)= -10кНм
20.
По полученным данным строим эпюру изгибающихмоментов Mx (готовую эпюру Qy перенесем из ранее
рассмотренной задачи)
21.
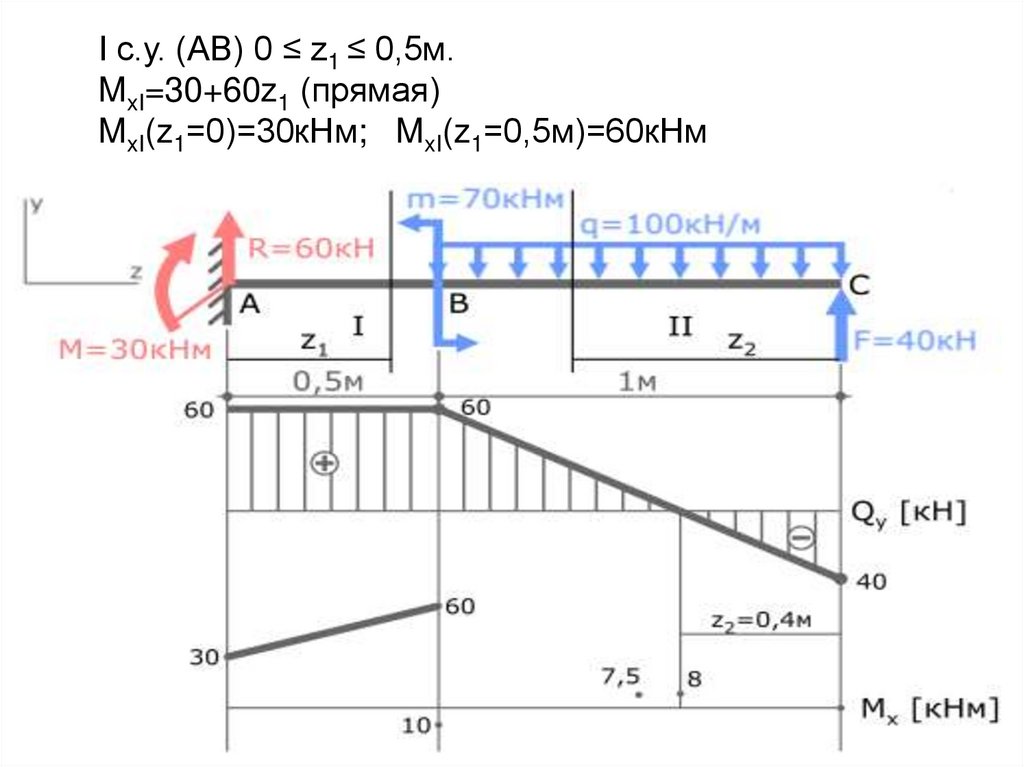
I с.у. (AB) 0 ≤ z1 ≤ 0,5м.MxI=30+60z1 (прямая)
MxI(z1=0)=30кНм; MxI(z1=0,5м)=60кНм
22.
II с.у. (BC) 0 ≤ z2 ≤ 1мMxII= -50z22+40z2 (парабола)
MxII(z2=0)=0; MxII(z2=0,5м)=7,5кНм; MxII(z2=1м)= -10кНм
Qy — первая производная от Mx. Поэтому в том месте,
где Qyпересекает базовую линию (т.е. Qy=0) на эпюре
Mx будет экстремум.
Рассчитаем значение экстремума эпюры Mx на II участке
балки. Для этого:выражение QyII приравняем к нулю
QyII=100z2-40=0
Выразим из него z2
z2=40/100=0,4м
Подставим z2 в выражение для MxII
2
z
MxII экстр = ( 2 = 0,4м) = - 50∙0,4 + 40∙0,4=8кНм
23.
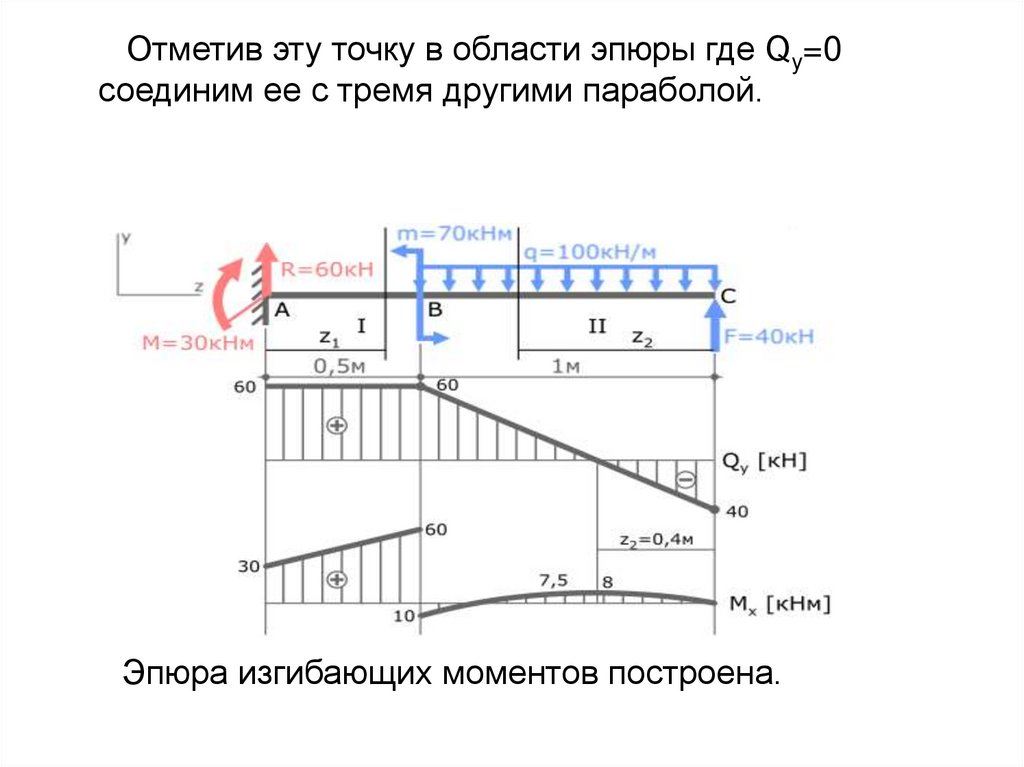
Отметив эту точку в области эпюры где Qy=0соединим ее с тремя другими параболой.
Эпюра изгибающих моментов построена.
24.
Проверка эпюры Mx.В сечениях балки, где приложен изгибающий момент,
на эпюре M будет скачок.
Здесь к балке приложено два момента: M в точке A и
m в точке B.
Проверим наличие скачков в указанных сечениях:
В точке A изгибающий момент M равен 30кНм.
Скачок значений на эпюре M также равен 30.
25.
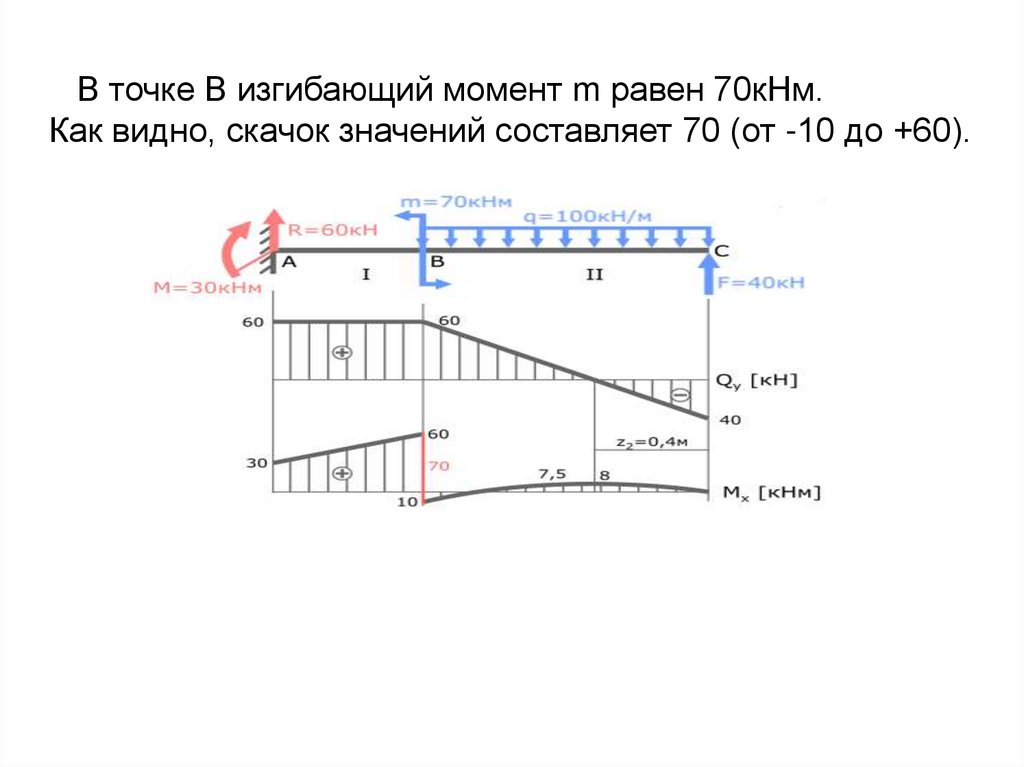
В точке B изгибающий момент m равен 70кНм.Как видно, скачок значений составляет 70 (от -10 до +60).
26.
Определение опасного сечения балкиОпасным называют сечение, в котором напряжения
вызываемые действием внешних усилий максимальны.
Определяющей является эпюра M, так как изгибающие
усилия для балки опаснее поперечных сил.
В данном случае по ранее построенным эпюрам Q и
M видно, что балка имеет одно опасное сечение в т. В.
Делаем проверку для этого сечения.
Сечение балки — двутавр №30, для которого
Wx = 472 см3.
σmax = Mmax / Wx =70∙106 / 472∙103=148 МПа < [σ]=160МПа











 physics
physics








