Similar presentations:
Sine, cosine, radians
1.
С12 Sine, cosine rulesRadians
#sinerule #cosinerule #bearing #radian #arclength
#sectorarea #trianglearea
2.
Sine rule3.
ExerciseCalculate the value of and :
a)
b)
4.
ExerciseTown is 6 km, on a bearing of 020, from town . Town is
located on a bearing of 055 from town and on a bearing of
120 from town .
Work out the distance of town from
a) town
b) town
5.
Let us find :6.
ExerciseWork out the value of
a)
b)
7.
ExerciseWork out the value of and
a)
b)
8.
• When the angle to be found is larger than the given anglethere are two possible results, because you can draw two
different triangles which satisfy the task
• These results and are connected:
In this example:
(to 3 s.f.)
9.
ExerciseWork out the possible values of and the corresponding
values of .
10.
Cosine rule11.
ExerciseWork out the value of the third side:
12.
ExerciseFrom a point a boat sails due north for 7 km to . The boat leaves and
moves on a bearing of 100 for 10 km until it reaches .
Calculate the distance of from .
13.
ExerciseWork out the size of the angle marked with * (to 3 s.f.):
14.
ExerciseA helicopter flies on a bearing of 080 from to , where km. It
then flies for 60 km to a point .
Given that is 80 km from calculate the bearing of from .
15.
Data1 side, 2 angles
2 sides, angle
2 sides, angle
3 sides
To find
side
angle
side
angle
Formula
Sine rule
Sine rule
Cosine rule
Cosine rule
16.
Area17.
ExerciseWork out the area of the given triangle:
18.
ExerciseWork out the value of :
19.
Angle is equal to 1 radian, when the length of arc isequal to .
20.
radians ,so
radian
21.
The length of an arcwhen is in radians.
22.
ExerciseThe sector of the circle radius cm
contains an angle of radians. Find the
length of the arc, giving your answers in
the form , where and are integers.
23.
ExerciseReferring to the diagram, find:
a) The perimeter of the shaded region
when radians.
a) The value of when the perimeter of
the shaded region is 14 cm.
24.
ExerciseIn the diagram is the diameter of a circle, centre and radius 2 cm. The
point lies on the circumference such that radians.
a) State the value, in radians, of .
The shaded region is a template for a
brooch.
(b) Find the exact value of the
perimeter of the brooch.
25.
The area of a sectorwhere is in radians
26.
ExerciseWork out the area of the shaded region:
(a)
(b)
(c)
27.
ExerciseThe arc of a circle, centre and radius cm, is such that
radians.
Given that the perimeter of the minor sector is 30 cm:
(a) Calculate the value of .
(b) Show that the area of the minor sector is 36 .
(c) Calculate the area of the segment enclosed by the chord
and the minor arc .
28.
ExerciseThe diagram shows a triangular plot of land. The sides , and have
lengths 12, 14 and 10 m respectively.
The lawn is a sector of a circle, centre
and radius 6 m.
(a) Show that to 3 s.f.
(b) Calculate the area of the flowerbed.
29.
ExerciseIn the diagram, is the diameter of a circle, centre and
radius cm, and radians.
Given that the area of is equal to
that of the shaded segment,
show that


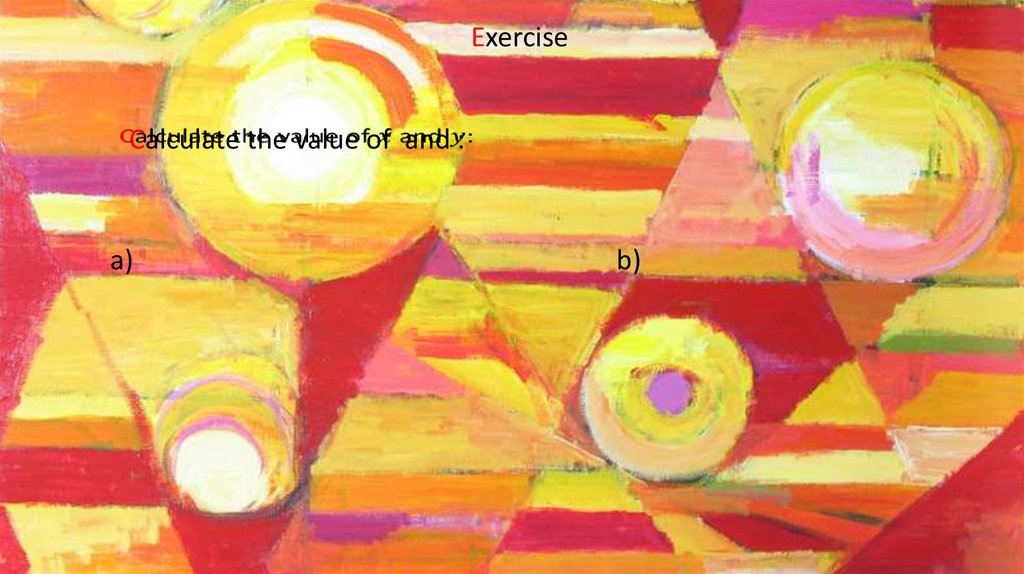

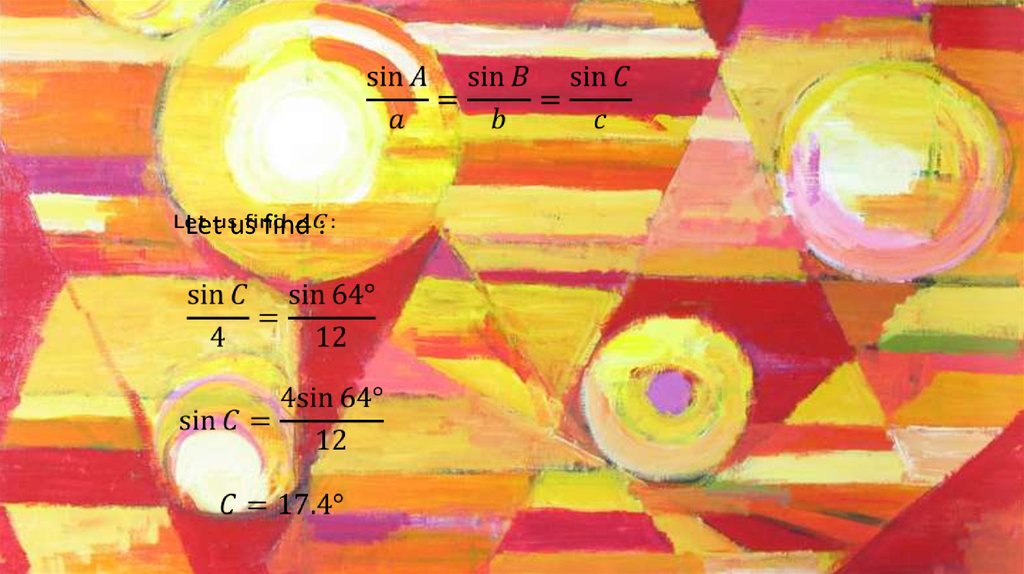




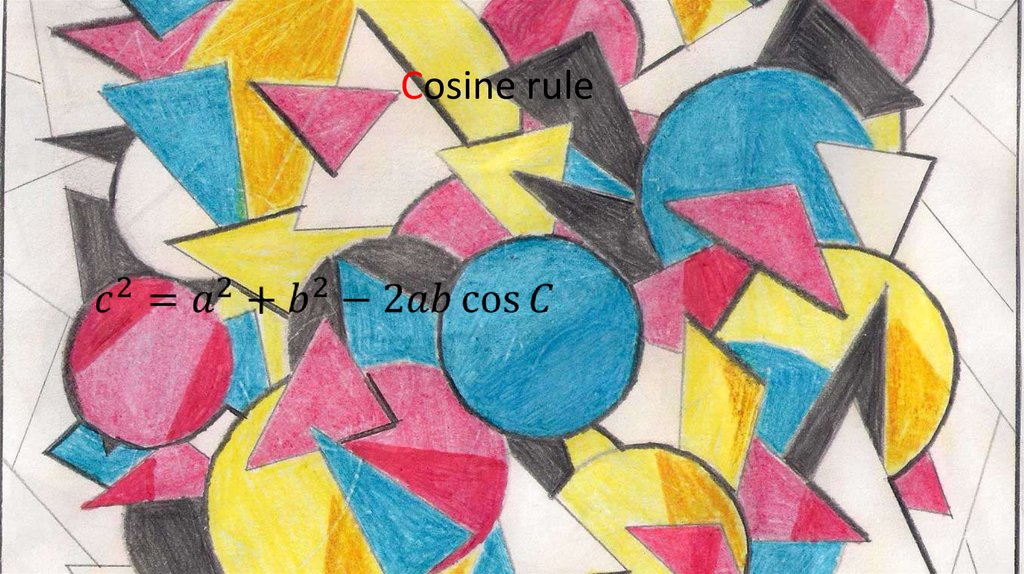


















 mathematics
mathematics english
english








