Similar presentations:
Погрешность интерполяционного многочлена Лагранжа
1. Погрешность интерполяционного многочлена Лагранжа
2.
Предполагаем, чтоf ( x) C n 1 a, b .
Ln(x) — многочлен Лагранжа: Ln ( xi ) f ( xi ) для всех i=0,...,n
[a,b] — отрезок, содержащий узлы x0, x1, ..., xn.
Найдем оценку отличия значения f(x) от значения Ln(x) в
точке
~
x a, b , не совпадающей ни с одним из узлов,
иначе, величину остаточного члена
Rn ( ~
x ) f (~
x ) Ln ( ~
x)
16.08.2018 13:40
2
3.
Запишем равенствоf ( x) Ln ( x) Rn ( x) Ln ( x) n 1 ( x) С
где
n 1 ( x) ( x x0 ) ( x x1 ) ( x – xn ) многочлен
определённый через узлы x0, x1, ..., xn
и С – некоторая постоянная (параметр).
Подберём параметр С так, чтобы f (x) обращалась в нуль
в точке , для которой делаем оценку, т.е. ~x a, b и
~
x xi , i 0, n .
К функции f (x) на каждом из отрезков
xi , xi 1 ,
i 0, n
применима теорема Ролля
16.08.2018 13:40
3
4.
Введём в рассмотрение функцию(t ) Ln (t ) n 1 (t ) C f (t )
R t
(t ) 0
если t x0 , x1 ,..., xn , ~
x всего (n+2) точки
(t ) 0
(n+1) точка на [a,b]
(t ) 0
n точек на [a,b]
...
( n 1) (t ) 0
16.08.2018 13:40
1 точка на [a,b]
по т. Ролля, если
функция в двух
точках равна 0,
то между этими
точками
существует
точка, в которой
производная
обращается в 0
4
5.
Итак, существует a, b : ( n 1) ( ) 0 .Так как
и
( n 1)
( n 1) ( x) 0 n 1
( x) C f ( n 1) ( x)
n ( n 1) ( x) (n 1)!
получаем (n 1)! С f ( n 1) ( ) 0
Отсюда
16.08.2018 13:40
f ( n 1) ( )
С
(n 1)!
5
6.
f ( x) Ln ( x) Rn ( x) f ( x) Ln ( x) n 1 ( x) Cn 1
( )
f ( x) Ln ( x) n 1 ( x)
n 1 !
f
Для остаточного члена получаем выражение
f ( n 1) ( )
Rn ( x) n 1 ( x)
(n 1)!
16.08.2018 13:40
6
7.
Точное представление f(x) через еёинтерполяционный многочлен Лагранжа Ln (x) :
f ( n 1) ( )
f ( x) Ln ( x) n 1 ( x)
(n 1)!
где a, b и зависит от x.
Можно оценить предельную абсолютную
погрешность интерполирования на отрезке a, b с
помощью формулы
max R( x) max n 1 ( x)
a ,b
16.08.2018 13:40
a ,b
max f ( n 1) ( x)
a ,b
(n 1)!
7
8.
Пример. Оценить с какой точностью можновычислить по формуле Лагранжа ln 100.5 , если ln 100,
известны значения ln 101, ln 102, ln 103.
f x ln x,
n 3, a x0 100, xn b 103, f 4 x 64 ,
x
6
max f 4 x
100 4
6
9
ln 100.5 L 100.5
0
.
5
0
.
5
1
.
5
2
.
5
3
10
100 4 4!
4 x
16.08.2018 13:40
8
9. Улучшение (уменьшение погрешности) интерполирования за счёт выбора узлов.
Задача. Дана функция f x на отрезке a, b ,дифференцируемая до (n+1)-го порядка. Выбрать
n 1 x было наименьшим.
узлы xi ,так чтобы max
a, b
16.08.2018 13:40
9
10. Многочлен Чебышева
Tn x cos n arccos x ,n 0;
T0 x cos 0 1,
n 1;
T1 x cos arccos x x,
n 2;
T2 x cos 2 arccos x
x 1
cos2 arccos x sin 2 arccos x
2cos2 arccos x 1 2x2 1
16.08.2018 13:40
10
11.
Обозначимarccos x ,
cos n 1 cos n cos n cos sin n sin
cos n 1 cos n cos n cos sin n sin
cos n 1 cos n 1 2cos n cos
Tn 1 x Tn 1 x 2 x Tn x
Tn 1 x 2 x Tn x Tn 1 x
16.08.2018 13:40
11
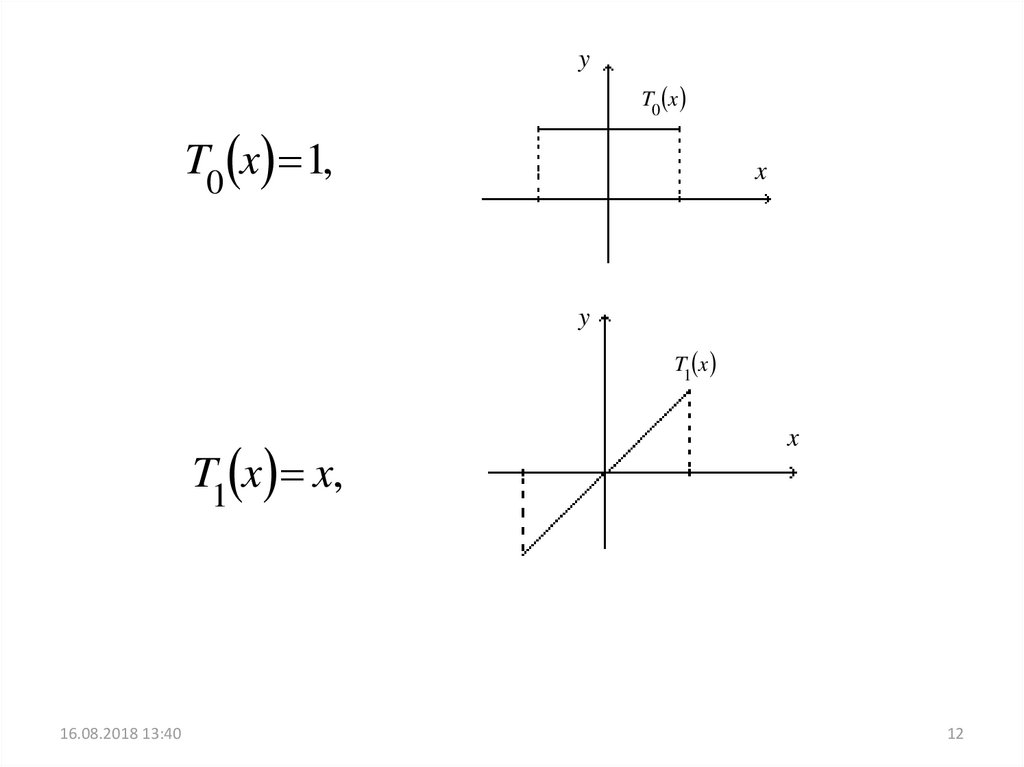
12.
yT0 x
T0 x 1,
x
y
T1 x
T1 x x,
16.08.2018 13:40
x
12
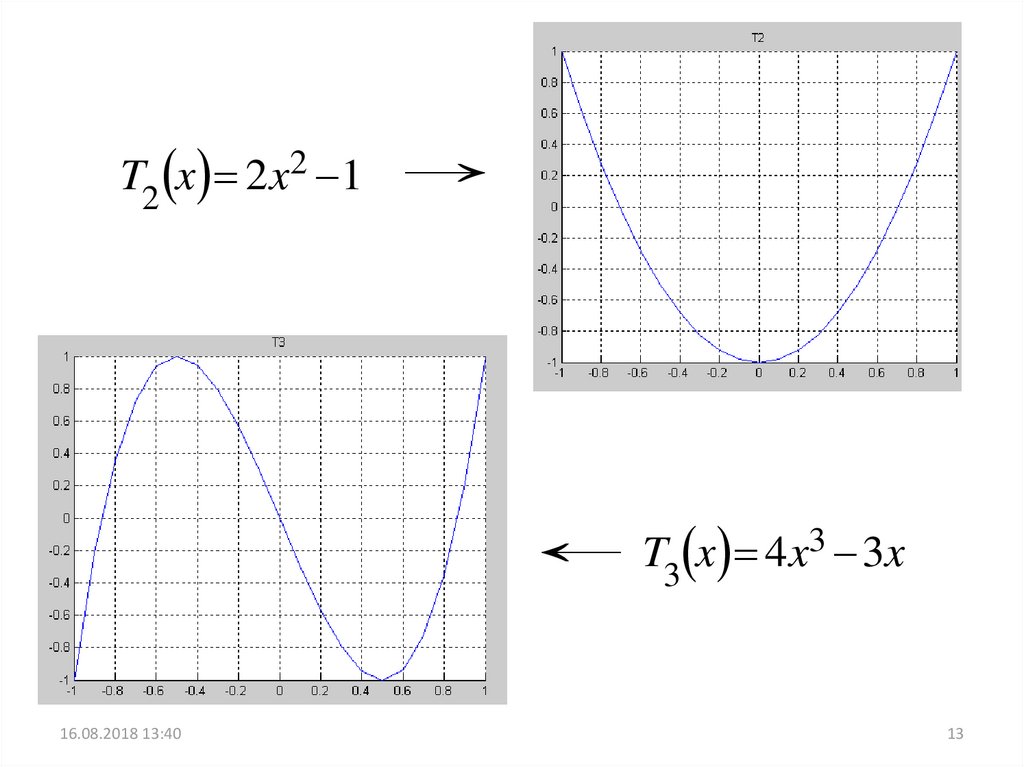
13.
T2 x 2 x2 116.08.2018 13:40
T3 x 4 x3 3x
13
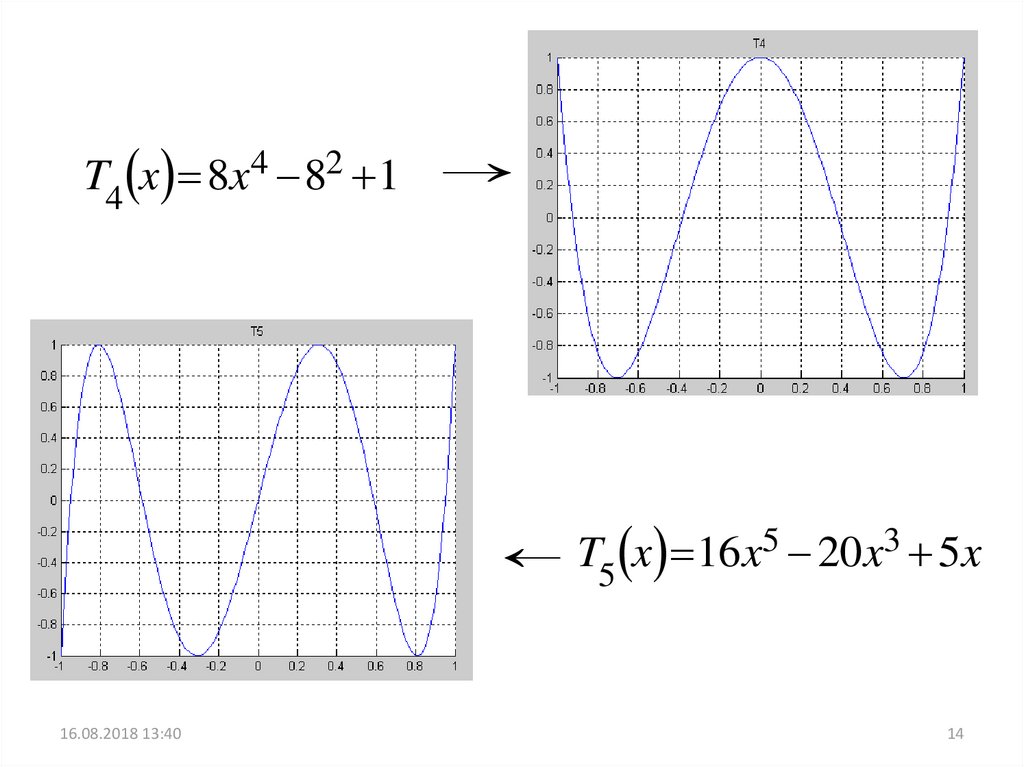
14.
T4 x 8x4 82 116.08.2018 13:40
T5 x 16 x5 20 x3 5x
14
15.
cos n arccosx 0n arccos x
arccos x
x cos
16.08.2018 13:40
2
2n
k
1 2k
1 2k
2n
15
16.
Замечание. Корни расположены неравномернои сгущаются к концам отрезка
Tn x 1
max
1, 1
cos n arccos x 1
n arccos x k
x cos
16.08.2018 13:40
k
n
, k 0, 1, 2,
16
17.
Теорема Чебышева. Из всех полиномов Pn x n-йстепени со старшим коэффициентом равным 1, у
1
полинома Tn x n 1 Tn x максимальное абсолютное
2
значение на интервале 1, 1 наименьшее, те есть
1
Pn x max Tn x n 1
max
2
1, 1
1, 1
Многочлен Чебышева – «многочлен, наименее
уклоняющийся от нуля».
16.08.2018 13:40
17
18.
Теорема. Корни многочлена2i 1
xi cos
,
2 n 1
минимизируют
n 1 x
max
1, 1
Tn 1 x
i 0, n
в оценке погрешности
интерполяционного многочлена. При этом
1
n 1 x x x0 x x1 x xn n Tn 1 x
2
и
1
n 1 x n
max
2
1, 1
16.08.2018 13:40
f n 1 x
Тогда
max
Rn x 1, 1n
2 n 1 !
18
19.
При интерполировании на произвольном отрезкелинейной заменой
2 x b a
t
b a
b a t b a
x
a, b
2
функция переводится на отрезок
1, 1
Рассматривается функция f t при этом корни многочлена
Чебышева Tn t
перейдут в
1
2k 1
xk b a cos
b a
2
2n
16.08.2018 13:40
19
20.
Оценка погрешности для этого случая будет такова:x
f
n 1
max
b
a
a , b
Rn x
n 1 !
22 n 1
n 1
Полученные результаты дают наилучшею оценку в
целом по всему отрезку a, b
Практическая рекомендация: если интерполяция может
выполняться с произвольным выбором узлов, то
целесообразно в качестве узлов выбирать нули
полиномов Чебышева.
16.08.2018 13:40
20










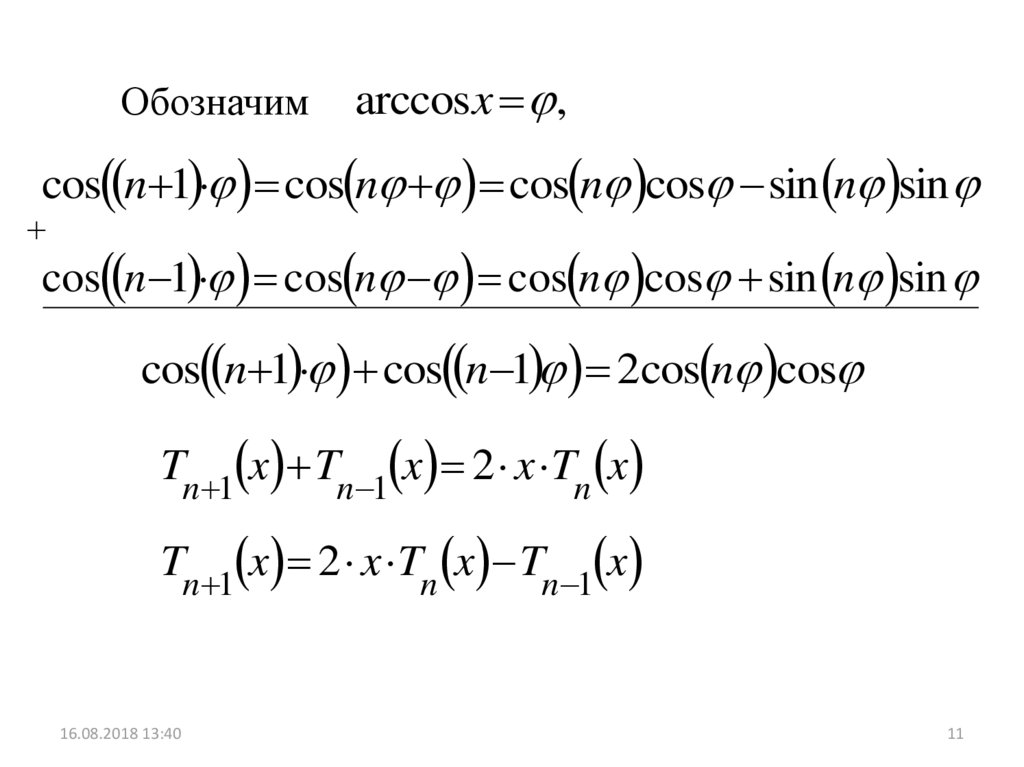
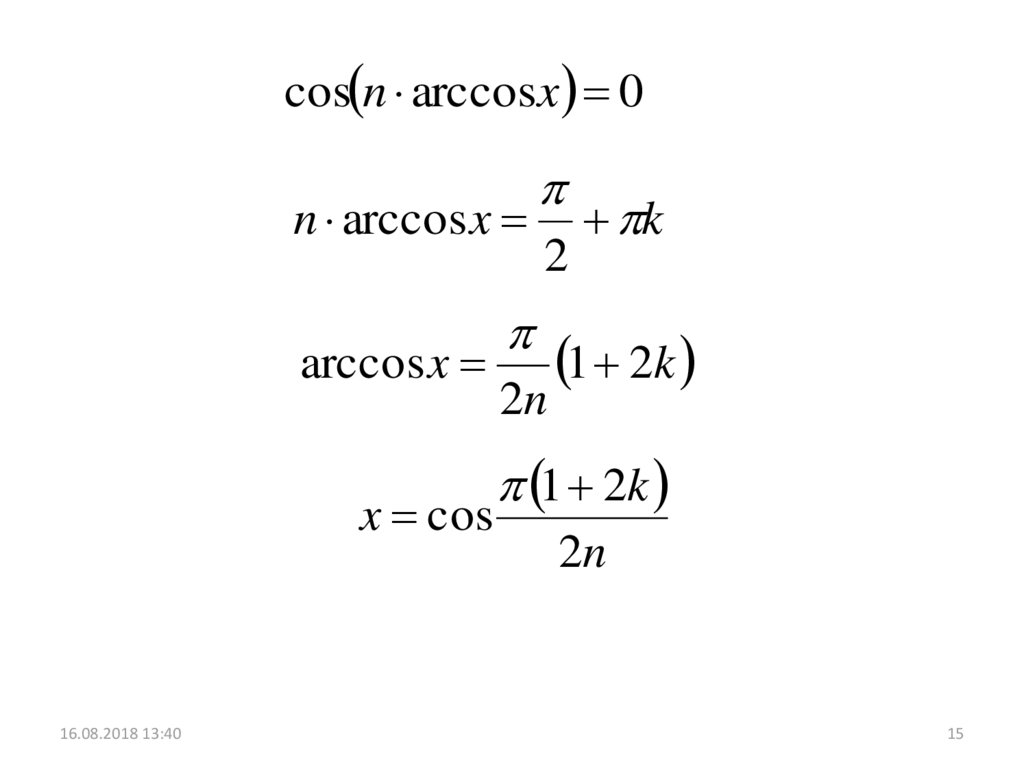





 mathematics
mathematics








