Теория вероятностей и математическая статистика

1. Лектор

Профессор
кафедры
математического
анализа Института Математики и Механики
им. Н.И. Лобачевского КФУ,
Каюмов Ильгиз Рифатович,
e-mail: [email protected]

2. Теория вероятностей и математическая статистика

3. 2017- Год Лобачевского в КФУ

• Никола́й Ива́нович Лобаче́вский (20
ноября 1792, Нижний Новгород — 12
февраля 1856, Казань) — русский
математик,
один
из
создателей
неевклидовой
геометрии,
ректор
Императорского Казанского университета
(1827-1845)

4. ОСНОВНАЯ ЛИТЕРАТУРА

5. Отцы-основатели

́ ли (нем. Jakob Bernoulli, 6
• Я́коб Бернул
января 1655, Базель, — 16 августа 1705, там
же) — швейцарский математик. Один из
основателей теории вероятностей и
математического анализа.
• Андре́й Никола́евич Колмого́ров (12
апреля 1903, Тамбов — 20 октября 1987,
Москва) — советский математик, один из
крупнейших математиков ХХ века.

6.

ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ (ТВ)
Законы природы и общества делятcя на
детерминистские
и
статистические.
К
детерминистским относятся такие законы, на
основании которых можно точно утверждать, что при
определенных условиях то или иное явление
обязательно произойдет.
Например, на основании закона движения планет
можно с точностью до минуты предсказать затмение
Солнца или Луны.
На основании же статистических законов можно
лишь с некоторой вероятностью предположить, что
при определенных условиях то или иное событие
произойдет.

7.

Например, синоптики говорят: «Во второй половине
дня возможен дождь».
Изучением детерминистских законов занимаются
точные науки: физика, химия и др. Изучением
статистических законов занимается математическая
статистика.
Теория вероятностей изучает закономерности
массовых однородных случайных процессов и является
теоретическим
обоснованием
математической
статистики.
Основные понятия ТВ
Одним из основных понятий ТВ является событие.

8.

Определение 1. Событие – это качественная
характеристика результата опыта или испытания.
События обозначаются заглавными буквами
латинского алфавита:
A, B, C или B1, B2, B3 и т.д.
Пример 1. Подбрасывается монета. Возможные
исходы (результаты) являются событиями:
A= {орел} , B= {решка} .
Пример 2. Студент сдает экзамен.
События:
B1= {отлично} , B2= { хорошо} ,
B3= { удовл.} , B4= { неуд.} .

9.

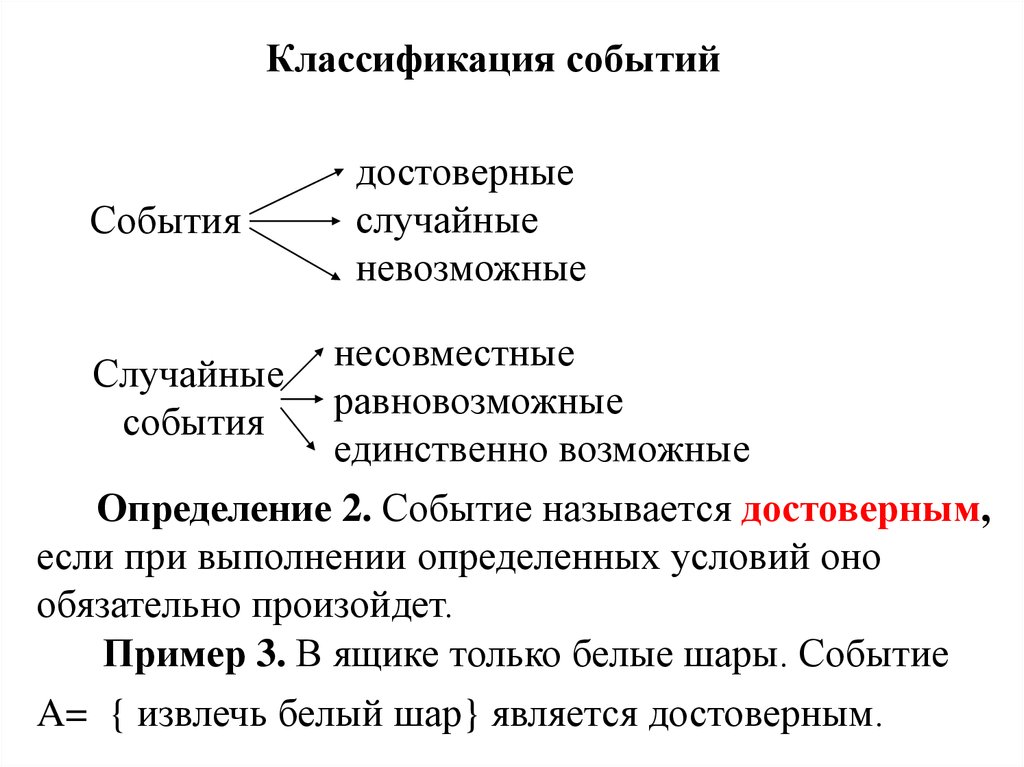
Классификация событий
События
достоверные
случайные
невозможные
несовместные
Случайные
равновозможные
события
единственно возможные
Определение 2. Событие называется достоверным,
если при выполнении определенных условий оно
обязательно произойдет.
Пример 3. В ящике только белые шары. Событие
A= { извлечь белый шар} является достоверным.

10.

Определение 3. Событие называется невозможным,
если при выполнении определенных условий оно
заведомо не произойдет.
Пример 4. В ящике только белые шары. Событие
A= { извлечь черный шар}
является невозможным.
Определение 4. Событие называется случайным,
если при выполнении определенных условий оно
может либо произойти, либо не произойти.
Пример 5. В ящике стандартные и бракованные
детали. Событие
A= {Взять стандартную деталь}
является случайным событием.

11.

Основным объектом внимания в ТВ являются
случайные события.
Определение 5. События называются
несовместными, если появление одного из них
исключает возможность появления другого события.
События A= {попадание} и B= { промах}
при одном выстреле несовместны.
Если появление одного из двух событий не
исключает возможность появления другого, то
события совместны.
События:
A= {Петров – первокурсник} и
B= {Петров – отличник} являются
совместными.

12.

Определение 6. Несколько событий называются
равновозможными, если появление любого из них не
более возможно, чем появление остальных.
Пример 6. Бросается игральная кость.
Выпадение на верхней грани любого количества очков
– события равновозможные.
Определение 7. События называются единственно
возможными, если при испытании одно из них
обязательно произойдет.

13.

Пример 7. События:
B1={отл.} , B2= {хор.}, B3= {удовл.}, B4= {плохо}
являются единственно возможными для одного студента
при одном испытании.
Определение 8.
Несколько событий образуют
полную группу событий, если они несовместны и
единственно возможны (см. Пр.7).
Определение 9. Множество всех взаимно или попарно
исключающих друг друга исходов случайного
эксперимента, которые вместе образуют полную
группу
событий,
называется
пространством
элементарных событий.

14.

Определение 10. Два события называются
противоположными, если они несовместны и
единственно возможны, т. е. образуют полную группу.
Например, события «экзамен сдан» и «экзамен не
сдан» являются противоположными при одном
испытании для одного студента, т.к. образуют полную
группу.
А события «холодно» и «жарко» не являются
противоположными, т.к. не образуют полной группы.
Событие, противоположное событию A,
обозначается A (не A).
Определение 11. Событие B называется
благоприятствующим событию A, если из появления
события B следует появление события A.

15.

Численной мерой возможности появления события A
является вероятность этого события.
Классическое определение вероятности
Рассматривается пространство элементарных событий.
Определение 12. Отношение числа M событий,
благоприятствующих событию A, к общему числу N
событий этой группы называется классической
вероятностью события A:
M
P ( A)
N
Классическая вероятность вычисляется теоретически
до проведения испытаний.

16.

Если событие A – достоверное, то все элементарные
события благоприятствуют событию A, то есть M=N.
Поэтому
P(A)=M/N=1.
Если событие A – невозможное, то ни одно
элементарное событие ему не благоприятствует, то
есть M = 0. Поэтому
P(A)=0/N=0.
Если событие A – случайное, то лишь часть
элементарных событий благоприятствуют событию A.
В этом случае 0<M<N. Следовательно, вероятность
случайного события
0<P(A)<1.

17.

Пример. В коробке 10 лотерейных билетов, из них
2 билета – выигрышные. Наудачу извлекается 1 билет.
Найти вероятность того, что этот билет –
выигрышный.
Дано:
N=10
M=2
P(A)=?
A = { выигрышный билет}
M
2 1
P( A)
N 10 5
При вычислении классической вероятности часто
используются формулы комбинаторики. Рассмотрим
элементы комбинаторики.

18.

ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Комбинаторика изучает количество комбинаций,
подчиненных тем или иным условиям, которые
можно составить из данного количества объектов.
1.Перестановки
Определение. Перестановками называются
комбинации, состоящие из одних и тех же n
различных элементов, отличающиеся только
порядком их расположения.
Например:

19.

Число различных перестановок из n элементов
равно:
Pn = n!

20.

где n! = 1*2*3*…*(n-1)*n
1! =1
2! =1*2 = 2
3! = 1*2*3 = 6
n! = (n-1)!*n
0! = 1
Пример. Перестановки из чисел 1,2 и 3:
1,2,3
2,3,1
3,1,2
2,1,3 1,3,2
3,2,1
P3 =3! =6
Задача. 8 девушек пошли в кино и приобрели
билеты в одном ряду. Сколько существует

21.

различных способов: а) рассадить девушек
в одном ряду; б) рассадить девушек так, чтобы
3 определенные девушки оказались рядом?
Решение:
Дано:
n = 8,
a) N = Pn = n! = 8! = 40320;
m=3
б) n – m + 1 = 8 – 3 + 1 =6,
a) N = ?
N1 = (n – m + 1)!* m! = 6!*3! =
б) N1 = ?
= 720*6 = 4320.

22.

1. Размещения
Определение. Размещениями называются
комбинации, составленные по m элементов из n
различных элементов, которые отличаются либо
составом, либо порядком расположения элементов.
Число размещений из n элементов по m равно:
m
n
!
n(n 1)(n 2)...(n m 1)
A =
(n m)!
n
m
Из этой формулы следует, что Рn = A * Pn – m
n

23.

Задача. На собрании необходимо выбрать
председателя, члена счетной комиссии и секретаря.
Найти число различных способов такого выбора,
если в собрании принимают участие 30 человек.
Решение:
Дано:
m
n = 30, N = А = А 3 =
n
30
m=3
N=?
30!
30 * 29 * 28 * 27!
30 * 29 * 28 24360
30 3 !
27!

24.

3. Сочетания
Определение. Сочетаниями называются
комбинации, составленные по m элементов из n
различных элементов, отличающиеся хотя
бы одним элементом.
В отличие от размещений в сочетаниях порядок
расположения элементов не имеет значения.
Число сочетаний из n элементов по m:
m
n
!
Cn = m!(n m)!

25.

m
Отсюда следует, что С n
m
m
m
n
A
=
m!
или
А n = С n*Рm
Задача. В группе 25 студентов. На концерт
популярной группы пожелали пойти все студенты
этой группы. На группу выделили 3 билета. Найти
число различных вариантов распределения
билетов.

26.

Дано:
Решение:
m
3
n = 25
m=3
N = Сn = C =
N=?
25!
25 * 24 * 23 * 22!
=
=
3! 25 3 !
3!*22!
25
25 * 24 * 23
=
= 2300.
6
При решении задач комбинаторики используют
следующие правила:

27.

1. Принцип суммы. Если некоторый объект А
может быть выбран из совокупности объектов m
способами, а другой объект В может быть выбран n
способами, то выбрать либо А, либо В можно
(m+n) способами.
2. Принцип произведения. Если объект А можно
выбрать из совокупности объектов m способами и
после каждого такого выбора объект В можно
выбрать n способами, то пара объектов (А,В)
в указанном порядке может быть выбрана
mn способами.

28.

Задача 1. В коробке 17 карандашей, на ощупь не
различимых. Из них 6 – красные, 2 – зеленые, 5 –
синие, а остальные – простые. Для раскраски картинки
девочке нужны красный и синий карандаши. Девочка,
не глядя, вынимает один карандаш. Найти число N
вариантов извлечь либо красный, либо синий
карандаш.
Решение:
Дано:
m = 6,
N = m + n = 6 + 5 = 11.
n=5
N=?

29.

Задача. В цветочном киоске имеются 40 роз, 50
хризантем, 30 гербер. Покупатель заказал букет
из 5 роз, 3 хризантем и 1 герберы. Найти число
различных вариантов составления букета.
Решение.
30!
50!
40!
5
3
1
.
.
N = C40 . C 5 . 30 = 5! 40 5 ! 3! 50 3 ! 1! 30 1 !
C
40 * 39 * 38 * 37 * 36 * 35! . 50 * 49 * 48 * 47!
=
6 * 47!
120 * 35!
.
30
*
29
!
.
= 658008 . 19600. 30 = 386908704000.
1 * 29!

30.

Пусть имеются n предметов, среди которых m
меченых. Необходимо умение решать два типа задач:
а) Наугад извлекаются k предметов (k ≤ m).
Вероятность того, что все извлеченные предметы
окажутся мечеными, равна: