Повторение. Треугольники

1. ПОВТОРЕНИЕ. ТРЕУГОЛЬНИКИ.

Выполнила
учитель математики
МБОУ Школа №99 г.о.Самара
Сычева Елена Александровна

2.

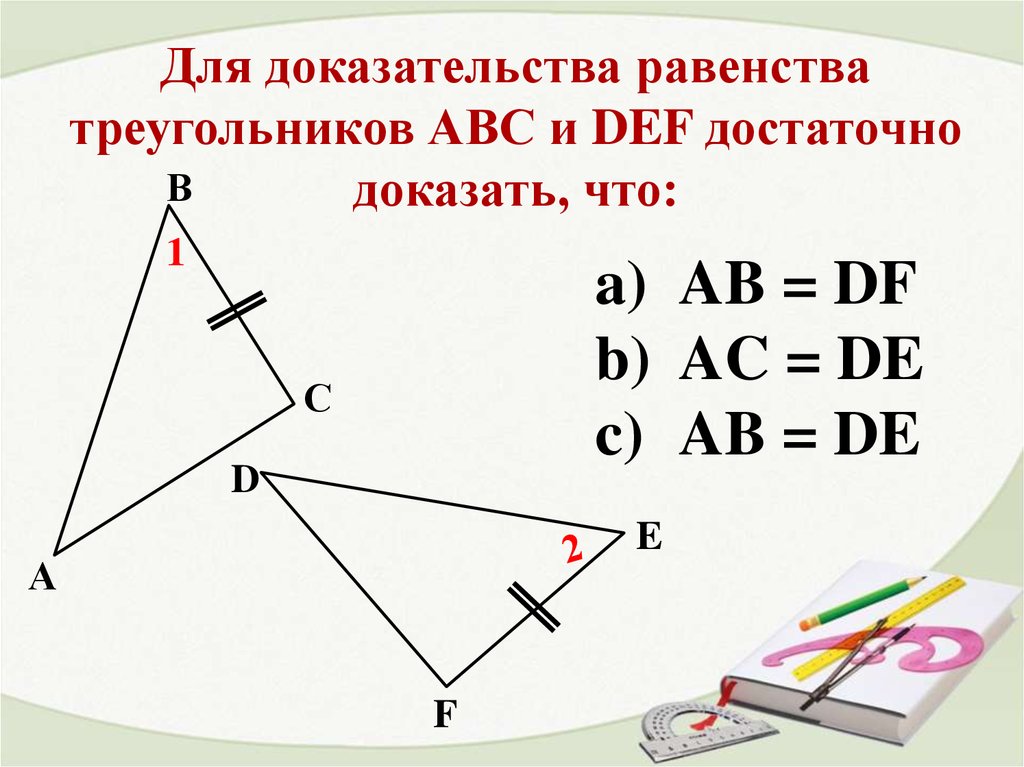
Для доказательства равенства
треугольников АВС и DEF достаточно
В
доказать, что:
1
a) AB = DF
b) AC = DE
c) AB = DE
С
D
E
А
F

3.

В
Для доказательства равенства
треугольников АВС и EDF достаточно
доказать, что:
E
1
А
a) ∠A = ∠D
b) ∠B = ∠D
c) ∠A = ∠E
С
2
D
F

4.

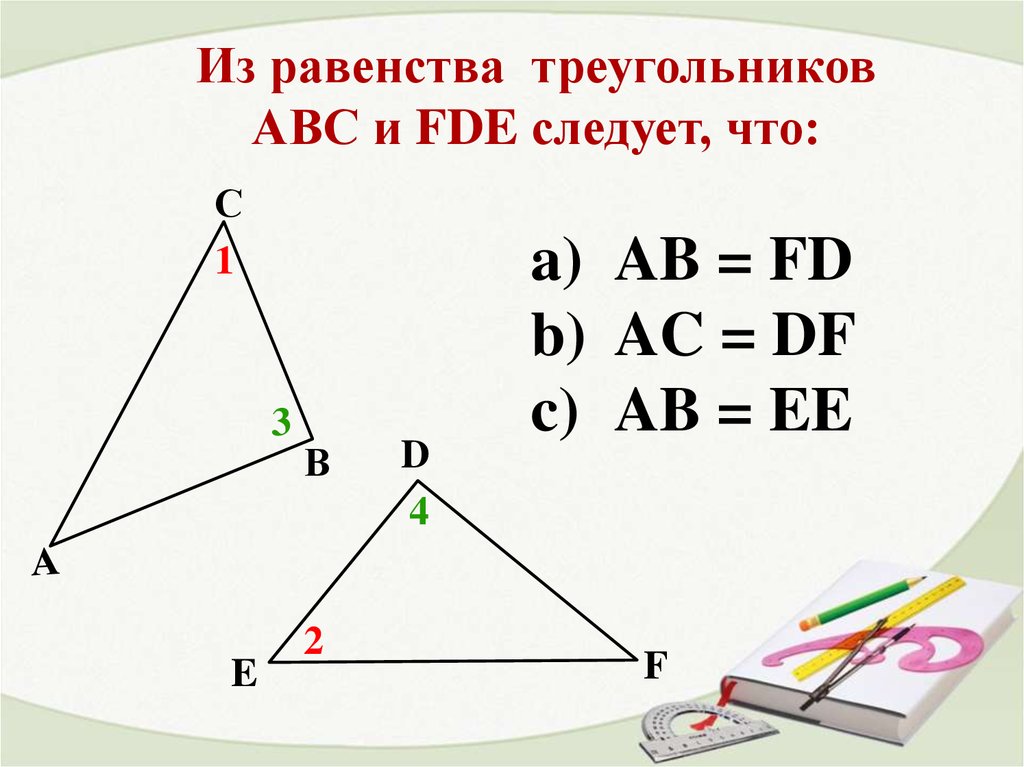
Из равенства треугольников
АВС и FDE следует, что:
С
1
3
E
В
2
D
4
a) AB = FD
b) AC = DF
c) AB = EE
F

5.

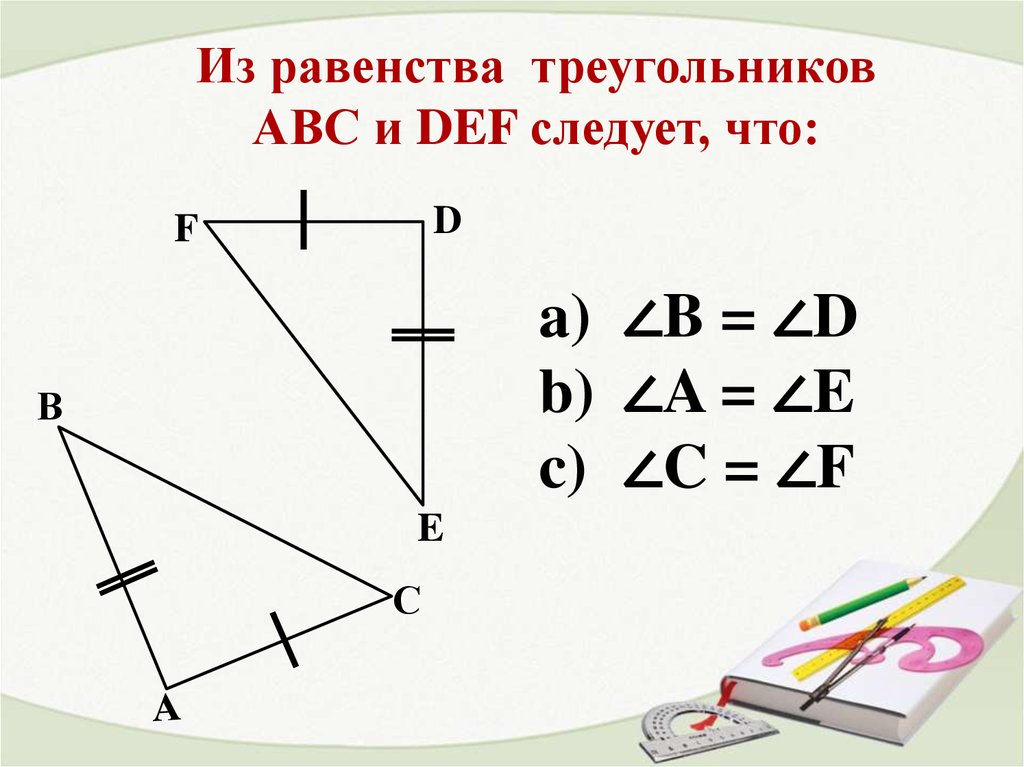
Из равенства треугольников
АВС и DEF следует, что:
D
F
a) ∠B = ∠D
b) ∠A = ∠E
c) ∠C = ∠F
В
E
С

6.

В ∆АВС все стороны равны, и в
∆DEF все стороны равны.
Чтобы доказать равенство ∆АВС и
∆DEF, достаточно доказать, что:
a) ∠B = ∠D
b) AB = DE
c) PABC = PDEF

7.

«Медиана в равнобедренном
треугольнике является
биссектрисой и высотой».
Это утверждение:
a) всегда верно
b) всегда неверно
c) может быть верно

8.

В каком треугольнике только одна
его высота делит треугольник на
два равных треугольника?
a) в любом
b) в равнобедренном
c) в равностороннем

9.

Если в треугольнике два угла
равны, то этот треугольник:
a) равнобедренный
b) равносторонний
c) прямоугольный

10.

Если треугольник
равносторонний, то:
a) он равнобедренный
b) все его углы равны
c) любая его биссектриса
является его медианой
и высотой

11.

ОТВЕТЫ
1.
2.
3.
4.
5.
6.
7.
8.
9.
С
С
А
С
В, С
С
В
А
А, В, С

12. ЗАДАЧА 1

В
1 2
ЗАДАЧА 1
Доказать:
DB – биссектриса
∠ADC.
С
A
D

13. ЗАДАЧА 2

Доказать:
O – середина АВ.
A
D
2
О
В
1
С

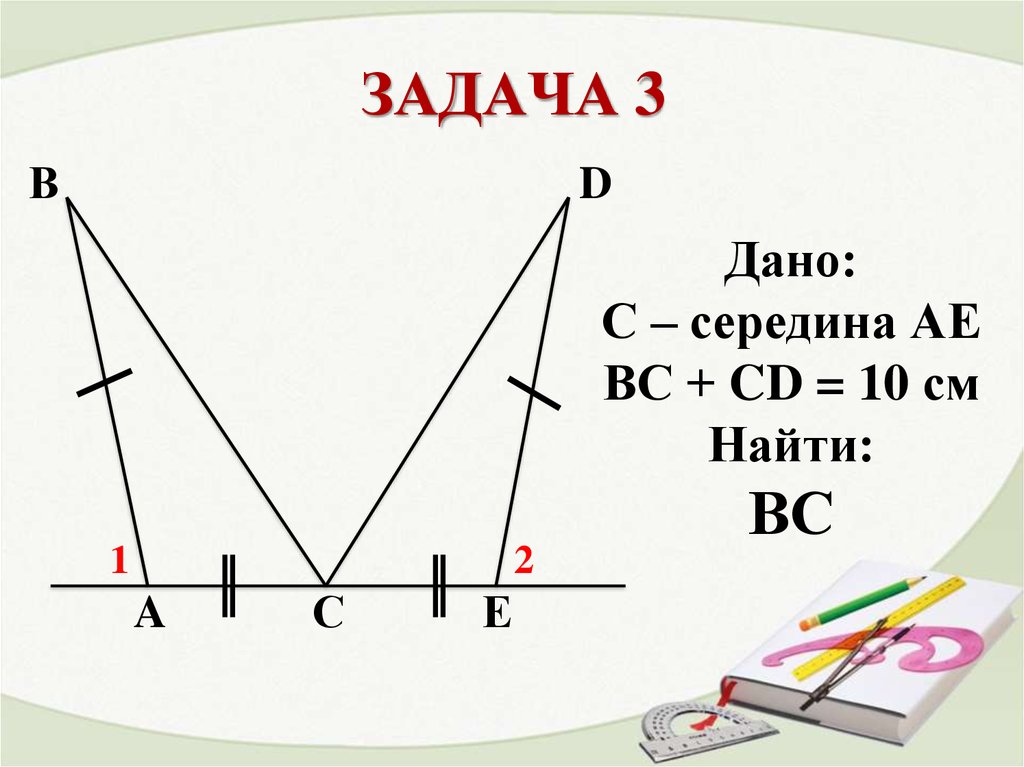
14. ЗАДАЧА 3

В
D
Дано:
С – середина АЕ
ВС + CD = 10 см
Найти:
1
2
A
С
Е
ВС

15. ЗАДАЧА 4

В
Доказать:
BC = DC
A
1
2
Е 3
С
4
D

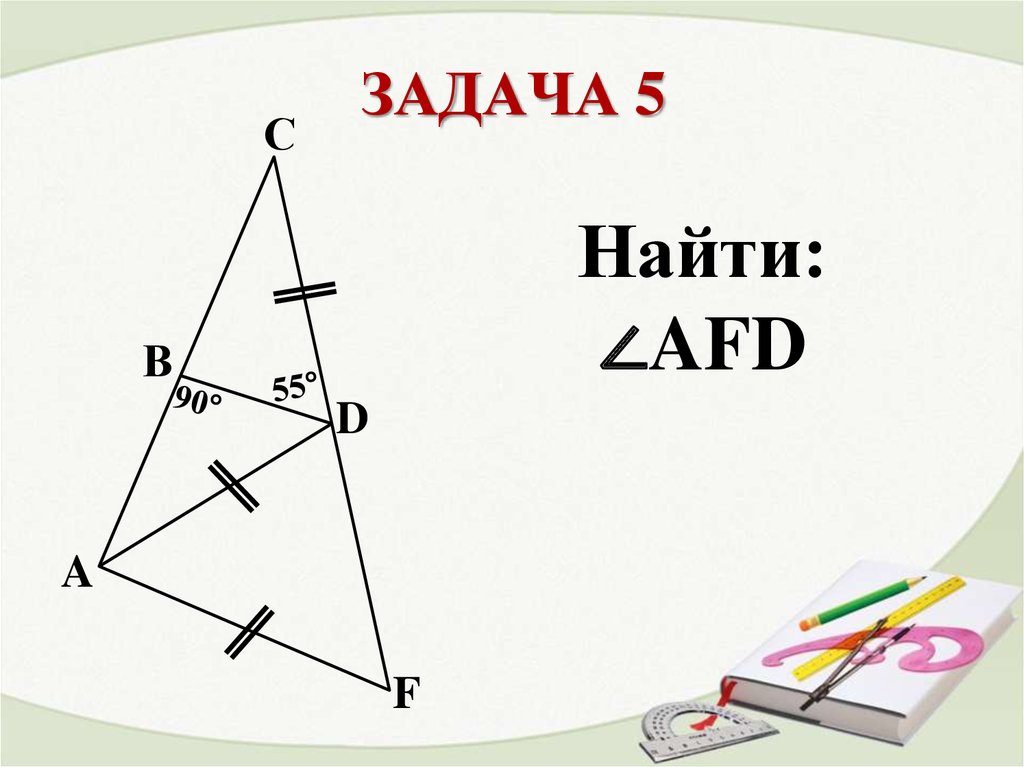
16. ЗАДАЧА 5

С
ЗАДАЧА 5
Найти:
∠AFD
В
D
A
F

17. ЗАДАЧА 6

В
130°
D
A
Найти:
∠ВAС
С

18. ЗАДАЧА 7

B
5 см
Найти:
АВ
125°
A
C 65°

19. ЗАДАЧА 8

B
Доказать:
∆АВС равнобедренный
A
Е
D
С

20. ЗАДАЧА 9

B
Дано: ВС = АD
Доказать: АВ = СD
Е
1
A
2
C
D

21. ЗАДАЧА 10

B
Доказать:
BD ⊥ AC
A
1
2
D
С

22.

Домашнее задание:
Повторить главу III
(вопросы 1 – 15 стр.48 - 49)
№328 - №332
(2 задачи на выбор)