692.50K

Category: $mathematics$ mathematics

Марковские цепи

1. Цепи Маркова

Определение и способы задания ЦМ
: T E R
1) t = 0, 1, 2, …
2)
X t X x1, x2 , ..., xn
3) Р X t x j X 0 xm ... X t 2 xk X t 1 xi
Однородные ЦМ:
t
pij pij
t
Р X t x j X t 1 xi pij
1

2. Цепи Маркова

Определение и способы задания ЦМ
: T E R
1) t = 0, 1, 2, …
2)
X t X x1, x2 , ..., xn
3) Р X t x j X 0 xm ... X t 2 xk X t 1 xi
t
Р X t x j X t 1 xi pij
Матрица
Однородные t
перехода ЦМ
pij pij
ЦМ:
p
p
...
p
11
12
1
n
P p 21 p 22 ... p 2n
... ...
...
p
p
...
p
n2
nn
n1
0 pij 1
n
pij 1
j 1
2

3. Цепи Маркова

Пример 1 (задача о погоде) Всем хороша Земля Оз, но только не
своей погодой. Здесь никогда не бывает двух ясных дней подряд. Если
сегодня ясно, то завтра с одинаковой вероятностью пойдет дождь или снег.
Если сегодня дождь или снег, то с вероятностью 0,5 погода не изменится.
Если все же она изменится, то в половине случаев снег заменится дождем
или наоборот, и лишь в половине случаев на следующий день будет ясная
погода.
Я
0
X Я , С, Д
Орграф ЦМ
Я
0.5
С Д
0.5 0.5
P 0.25 0.5 0.25
0.25 0.25 0.5
Я
С
Д
0.5
0.25
0.25
0.5
0.5
Д
0.25
С
0.25
3

4. Многошаговый переход в ЦМ

Какова вероятность за m шагов перейти из
состояния хi в состояние х j ?
Гипотеза Нk: через s шагов (s<m) перешли в
состояние хk
pij m
n
pik s pkj m s
i , j 1, n
k 1
P m P s P m s
- уравнение Колмогорова-Чепмена
4

5. Многошаговый переход в ЦМ

Уравнение
Колмогорова-Чепмена
Теорема
0 0.5
P m P
m
P
P m P s P m s
0.5
0.25
0.25 0.5 0.25
2
P 0.188 0.438 0.375
0.25 0.25 0.5
0.188 0.375 0.438
0.18
3
P 0.20
0.199 0.4
0.188 0.406 0.406
5
P 0.203 0.406 0.391
P 0.2
0.203 0.391 0.406
0.2
3
Следствие
0.375 0.375
0.4
0.20
0.4
0.399
0.399 0.4
n
T
T
m p j m pk 0 pkj m
Rm R0 P
k 1
j 1, n
5

6. Классификация состояний ЦМ

Пример 2
0.25
x1
0.75
x3
1
x2
1
0.25
0.5
x4
Состояние х j
достижимо из
состояния хi
m : pij m 0
Если состояния взаимодостижимы, то они
принадлежат одной сильной компоненте
орграфа.
Множество состояний С замкнуто, если
xi C и x j C pij 0
6

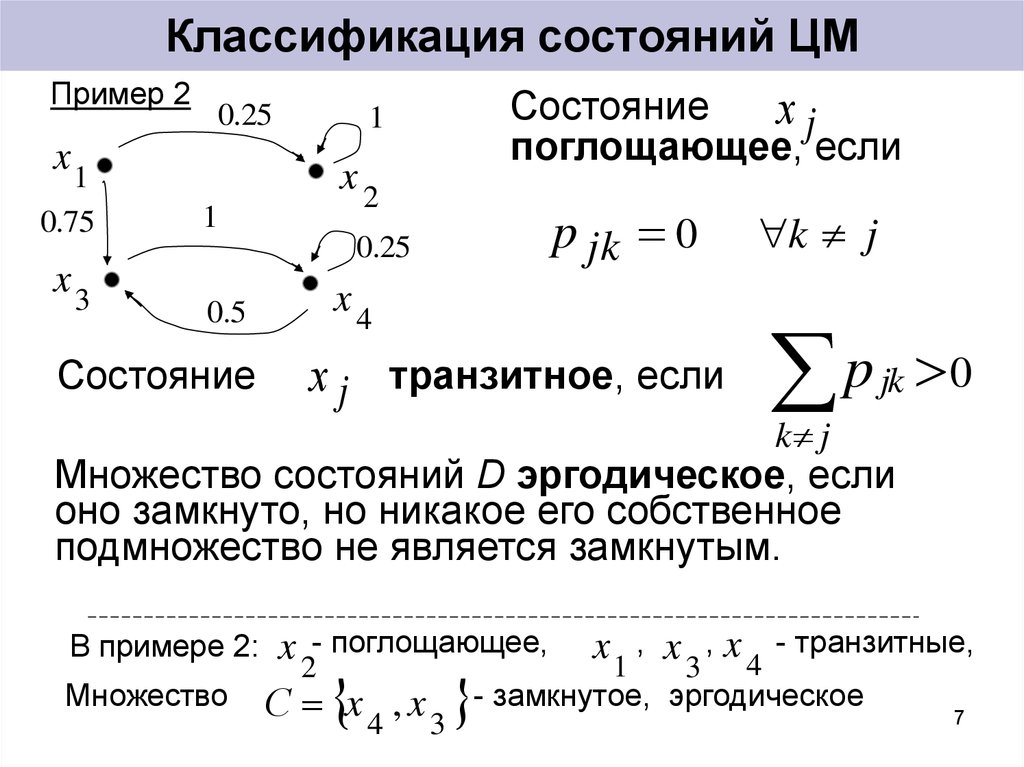
7. Классификация состояний ЦМ

Пример 2
0.25
x1
0.75
x3
1
Состояние
хj
поглощающее, если
1
x2
p jk 0
0.25
0.5
Состояние
x4
х j транзитное, если
k j
p
jk
0
k j
Множество состояний D эргодическое, если
оно замкнуто, но никакое его собственное
подмножество не является замкнутым.
В примере 2:
Множество
x 2- поглощающее, x 1 , x 3 , x 4 - транзитные,
С x 4 , x 3 - замкнутое, эргодическое
7

8. Переход в эргодическое состояние

Теорема (о переходе в
эргодическое состояние)
pэ t t
1
Если конденсация орграфа ЦМ слабосвязна,
то независимо от начального состояния
вероятность перейти за t шагов в эргодическое
состояние стремится к 1 при t
В конденсации орграфа эргодическому множеству
соответствует сильная компонента без исходящих
дуг
r: y Э х Э d x, y r
p 0: х Э pэ r p
8

9. Переход в эргодическое состояние

Теорема (о переходе в
эргодическое состояние)
pэ t t
1
r p э r 1 p
2) Вторая серия из числа шагов t r
2
p
2
r
1 p
э
… …
1) Пусть число шагов t
r
k
pэ kr 1 p
k
pэ t 1
0 p 1 1 p 0
t
k) k серия из числа шагов t
k
Изучение ЦМ:
I этап: до перехода в эргодическое множество;
II этап: поведение внутри эргодического множества9

10. Поглощающие цепи Маркова

Определение. ЦМ – поглощающая, если имеет
хотя бы одно поглощающее состояние x p и для
любого непоглощающего состояния x h
p
hp
k 0
k 0
Пример 3
Некий игрок, имея не более трех тугриков, начинает
игру в наперстки (при угадывании получает тугрик,
при ошибке – отдает). Заранее он решает, что
прекращает игру, как только его капитал составит три
тугрика.
1
0
1
X 0,1, 2, 3
2
3
1
3
2
3
1
2
3
1
3
10

11. Поглощающие цепи Маркова

Канонический вид матрицы перехода
x x ,..., x поглощающие состояния ЦМ:
xm 1, xm 2 ,..., xn непоглощающие состояния
1,
2
m
Матрица
перехода ЦМ
I
P
R
O
Q
I m m
O m n m
R n m m
Q n m n m
11

12. Поглощающие цепи Маркова

Пример 3
1
1
0
1
Некий игрок, имея не более трех тугриков, начинает игру в наперстки (при
угадывании он получает тугрик, при ошибке – отдает). Заранее он решает,
что прекращает игру, как только его капитал составит 3 тугрика.
2
3
2
3
1
3
2
3
0
0
2
3
0
0
1
3
0
0
1
0 x1
3 x2
1 x3
2 x4
Канонический вид
3
Матрица перехода
1
2
P 3
0
0
X 0,1, 2, 3
0
0
1
3
1
1
0
P 2
3
0
0
0
1
0
0
0
1
3
2
3
0
0
1
3
0
12

13. Поглощающие цепи Маркова

I
Теорема 1. Для поглощающей ЦМ
P
R
с матрицей Р справедливо
t
а) Q 0
O
Q
t
б) существует матрица, обратная к матрице Е-Q,
и ее можно найти по формуле
Е Q
1
Е Q Q 2 ...
Теорема о переходе в
эргодическое состояние
Е Q Е Q Q
Е Q
1
N
2
а)
... Q
t 1
t
Q
t 0
E Q
t
б)
- фундаментальная
матрица ЦМ
13

14. Поглощающие цепи Маркова

Теорема 2. Пусть в начальный
момент времени поглощающая ЦМ
I O
P
находилась в состоянии x i .
Тогда элемент n ij фундаментальной
R Q
матрицы N равен среднему времени
нахождения ЦМ в непоглощающем
1
Е Q N
состоянии x j до момента
поглощения.
Рассмотрим СВ
1, если X t x j
Y j t 0, если X x
t
j
M Y j t X 0 xi M Y j t X 0 xi
t 0
t 0
14

15. Поглощающие цепи Маркова

16. Поглощающие цепи Маркова

17. Поглощающие цепи Маркова

Теорема 2. Пусть в начальный
момент времени поглощающая ЦМ
I O
P
находилась в состоянии x i .
Тогда элемент n ij фундаментальной
R Q
матрицы N равен среднему времени
нахождения ЦМ в непоглощающем
1
Е Q N
состоянии x j до момента
поглощения.
Следствие. Пусть в начальный момент времени
поглощающая ЦМ находилась в состоянии x .
i
Среднее число шагов до поглощения равно
сумме элементов i-ой строки матрицы N.
17

18. Поглощающие цепи Маркова

Пример 3
(игра в «наперстки»)
0 x
3 x
X 0,1, 2, 3
1
2
1 x
2 x
3
4
1
0
P 2
3
0
0
0
1
0
0
0
1
3
2
1
E Q
2 3
3
I O
P
R Q
Е Q 1 N
0
0
1
3
0
0
Q
2 3
1
3
0
3
1
9
N 7
6 7
7
9
7
1
3
18

19. Поглощающие цепи Маркова

Теорема 3. В поглощающей ЦМ с
матрицей перехода (*)
вероятность перехода в заданное
поглощающее состояние
определяется матрицей B=NR.
I
P
R
O
(*)
Q
Е Q 1 N
Пусть в начальный момент времени
x
поглощающая ЦМ находилась в состоянии i .
Обозначим b
- вероятность попасть в k-ое
поглощающееikсостояние
В момент времени t =1 возможны гипотезы:
а ) X 1 xk
б ) X1 xl l k 1 l m
в ) X 1 xr m 1 r n
19

20. Поглощающие цепи Маркова

Теорема 3. В поглощающей ЦМ с
матрицей перехода (*)
вероятность перехода в заданное
поглощающее состояние
определяется матрицей B=NR.
I
P
R
O
(*)
Q
Е Q 1 N
По формуле полной вероятности
bik pik 1 pil 0
n
pir brk
r m 1
В матричной
форме
B R Q B
k 1, m
i m 1, n
B N R
20

21. Поглощающие цепи Маркова

Пример 3 (игра в «наперстки»)
I
0 x
1
1 x
X 0,1, 2, 3
3
1
0
P 2
3
0
2
R 3
0
0
0
1
0
0
0
1
3
2
0
1
3
3
P
R Q
Е Q 1 N
3 x
2
2 x
4
0
0
1
3
0
9
N 7
6 7
3
7
9
7
6
B N R 7
4 7
1
7
3
7
O
21

22. Эргодические цепи Маркова

Эргодическая ЦМ: нет поглощающих
состояний и из любого состояния можно
попасть в любое другое.
Орграф эргодической ЦМ сильносвязен.
Стационарный режим ЦМ:
при достаточно больших t вероятность
нахождения в состоянии хi не зависит от
того, каким было начальное состояние
системы.
Достаточное условие существования
стационарного режима – регулярность.
ЦМ называется регулярной, если
k : pij k 0 i, j 1, n
22

23. Эргодические цепи Маркова

Теорема Если ЦМ с матрицей перехода Р
регулярна, то
, где все строки
t
а) P W матрицы W
одинаковы
t
wij u j j , i 1, n
б) существует единственный вектор
u u1, u 2 ,...,u n
T
T
такой, что
n
u j 1
j 1
и
T
u P u
T
23

24. Эргодические цепи Маркова

Пример 1 (задача о погоде)
uT u1,u2 ,u3
u j 1 и uT P uT
T
n
j 1
Я
0.5
0.5
0.25
0.25
0.5
u1 0.25u 2 0.25u3
u 2 0.5u1 0.5u 2 0.25u3
u 0.5u 0.25u 0.5u
1
2
3
3
u1 u 2 u3 1
u1 1
5
4u1 u 2 u3 0
2
u
5
2u1 2u 2 u3 0 2
2
u1 u 2 u3 1
u
3
5
0.5
Д
0.25
С
0.25
0 0.5 0.5
0
.
25
0
.
5
0
.
25
P
0.25 0.25 0.5
Т
1 2 2
u , ,
5 5 5
Т
24

25. Эргодические цепи Маркова

Пример 1 (задача о погоде)
Я
0.5
0.5
0.25
0.25
0.375 0.375
0.5
2
P 0.188 0.438 0.375
0.188 0.375 0.4383
5
P 0.2
0.2
0.4
0.4
0.399
0.399 0.4
0.5
Д
0.188 0.406 0.406
P 0.203 0.406 0.391
0.199 0.4
0.25
0.203 0.391 0.406
0.25
С
0.25
0 0.5 0.5
0
.
25
0
.
5
0
.
25
P
0.25 0.25 0.5
0.2 0.4 0.4
10
P
0.2 0.4 0.4
0.2 0.4 0.4
Т
1 2 2
u , ,
5 5 5
Т
25

English Русский Rules