Similar presentations:
Матрицы, операции над матрицами
1.
Лекция N2Тема: Матрицы, операции над матрицами
Опр. 1 Матрицей размерности mxn
называется таблица чисел
a11
A a21
a
m1
a1n
a2 n .
amn
2.
Если число строк не равно числу столбцов,то матрица называется прямоугольной
Если число строк равно числу столбцов,
то матрица называется квадратной
Примеры
1 2
A
;
3 4
1 2 0
B
;
4 5 6
квадратная
прямоугольная
A(2 2)
B(2 3)
3.
aij- элементы матрицы
i
- номер строки
j
- номер столбца
4.
Опр. 2 Матрица называется нулевой,если все элементы равны нулю.
Опр. 3 Матрица E называется
единичной, если она квадратная, на
главной диагонали стоят единицы, а
вне диагонали - нули.
Примеры
1 0
0 0
;
; E
0 1
0 0
1 0 0
E 0 1 0 .
0 0 1
5.
Операции над матрицами1. Сложение
3 1
1 2
Пример. A
B
.
;
0 1
2 4
Найти
A B
.
6.
Для сложения матриц нужно сложитьсоответствующие элементы.
2 1 4 3
1 3
A B
.
0 2 1 ( 4) 2 3
Складывать можно матрицы, имеющие
одинаковые размерности.
7.
2. Умножение на числоПример.
1 2 3
A
;
4 0 1
Найти
2 A.
8.
Чтобы умножить матрицу на число,нужно каждый элемент умножить на это
число.
2 1 2 2 2 3 2 4 6
2A
.
2 4 2 0 2 1 8 0 2
9.
3. Умножение матрицA(n m) B(m k ) C (n k )
Число столбцов матрицы A должно
совпадать с числом строк матрицы B.
10.
Пример.1 2 0
A
;
3 1 1
Найти
A B.
2 0
B 1 3 .
0 1
A B C;
A(2 3) B(3 2) C (2 2).
11.
C11 C12C
;
C21 C22
C11 1 2 2 1 0 0 4;
C12 1 0 2 3 0 1 6;
C21 3 2 1 1 ( 1) 0 7;
C22 3 0 1 3 ( 1) 1 2.
12.
4 6C
.
7 2
A B B A.
Если A B B A, то матрицы A и B
называются коммутативными.
13.
4. Возведение в степеньТолько для квадратных матриц
A A A.
2
Дома
3 4
A
;
2 3
Найти:
0 1
B
.
2 3
A 2B; A B;
B A;
A ; ( A B) .
2
2
14.
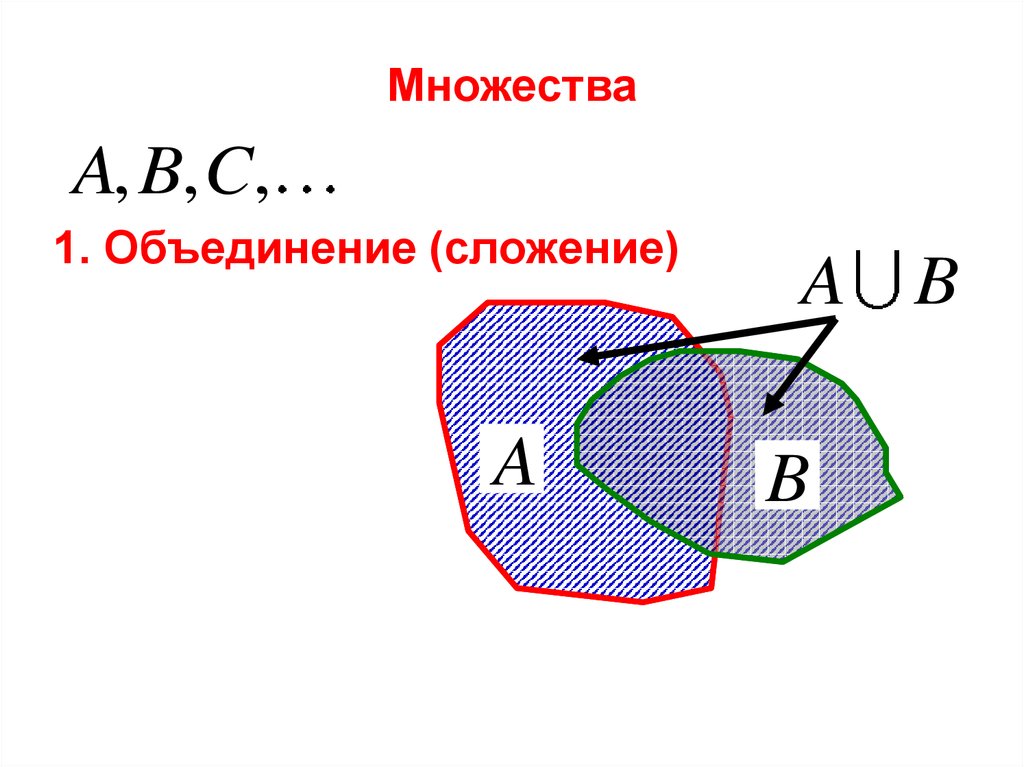
МножестваA, B, C,
1. Объединение (сложение)
A B
Пример.
A {1,2,3}
B {3,4}
A B
A
B
A
B {1,2,3,4}
15.
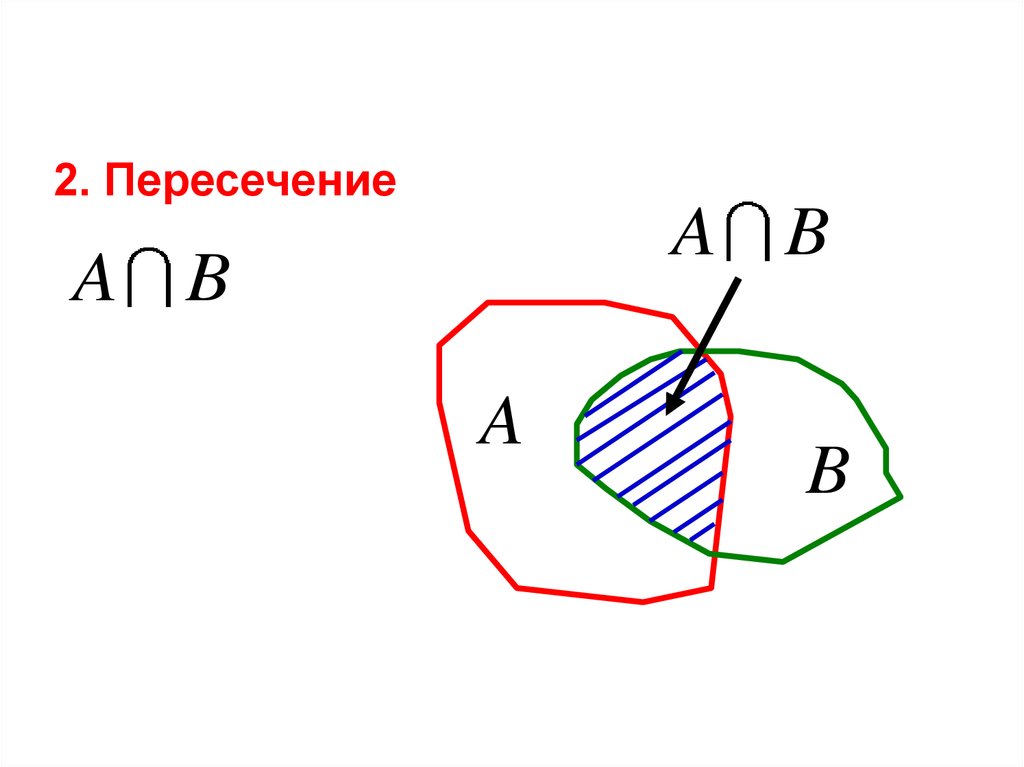
2. ПересечениеA B
A B
Пример.
A {1,2,3}
B {3,4}
A
B
A
B {3}
16.
Тема:Матрицы: элементарные
преобразования строк, приведение к
ступенчатому виду и виду Гаусса.
Ранг матрицы
17.
Опр. 1 Элементарными преобразованиямистрок матрицы называются:
1) Перестановка местами двух строк
2) Замена строки суммой этой строки и
некоторой другой, умноженной на
число
3) Умножение строки на ненулевое
число
18.
Аналогично вводятся элементарныепреобразования столбцов.
Опр.2 Опорным элементом строки
называется первый слева ненулевой
элемент этой строки.
19.
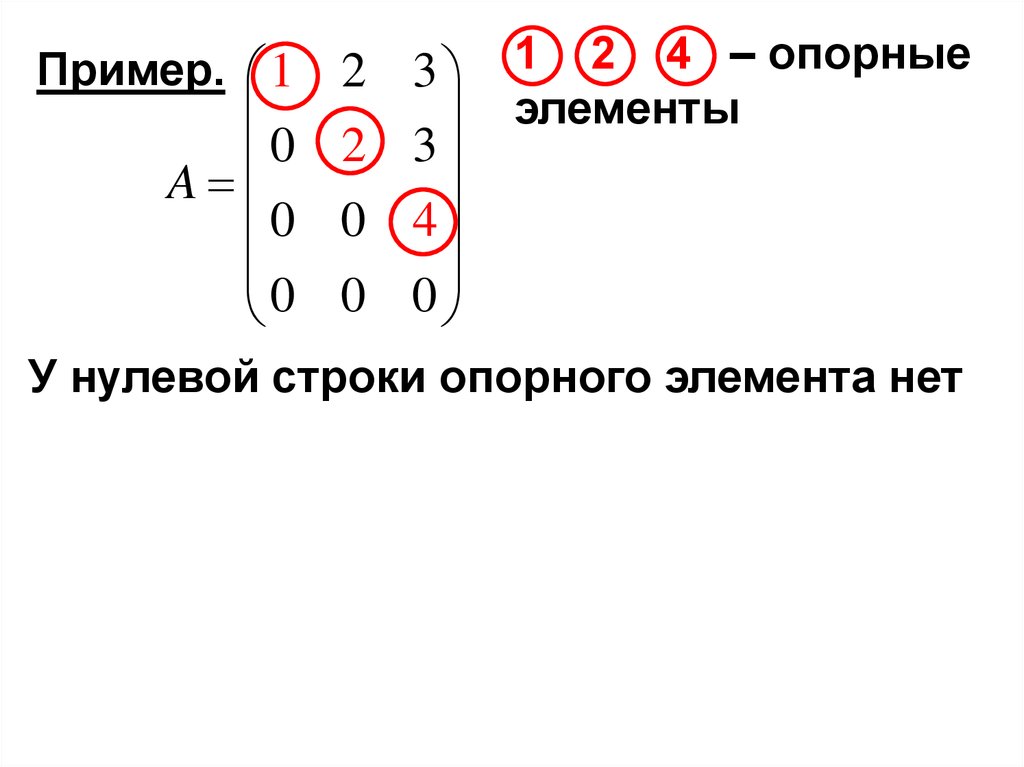
Пример. 12 3
0
2
3
A
0 0 4
0 0 0
1 2 4 – опорные
элементы
У нулевой строки опорного элемента нет
20.
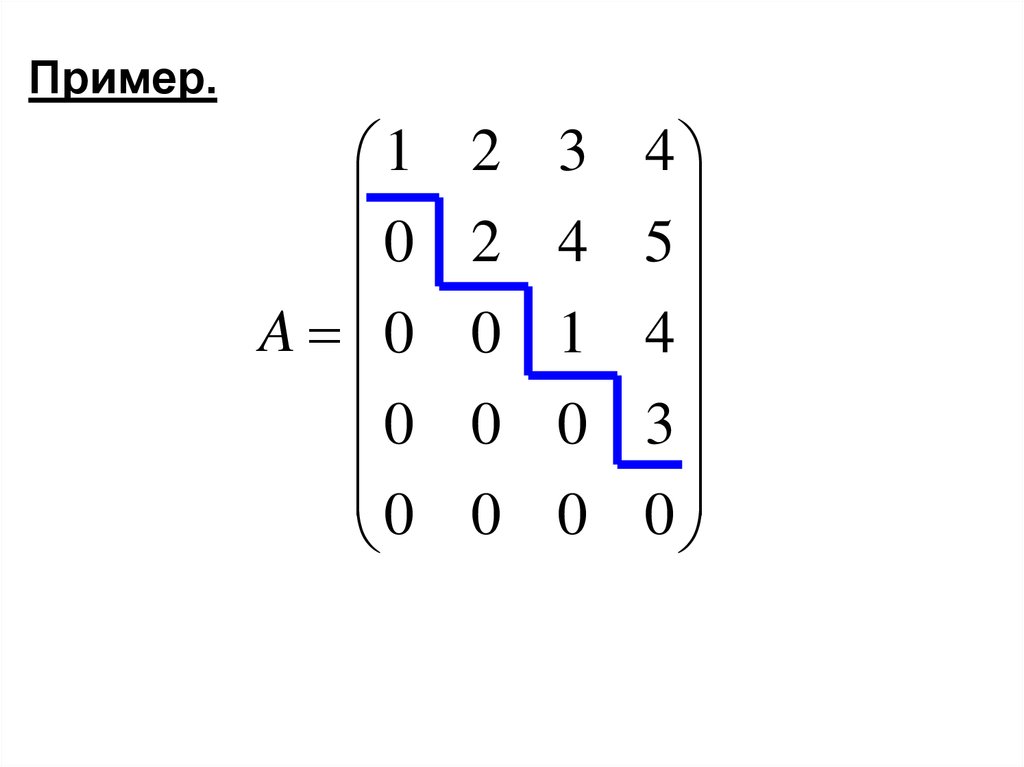
Опр. 3 Матрица называетсяступенчатой, если опорный элемент в
каждой последующей строке
расположен правее, чем в предыдущей.
Если строка нулевая, то все
последующие строки также нулевые.
21.
Пример.1
0
A 0
0
0
2 3 4
2 4 5
0 1 4
0 0 3
0 0 0
22.
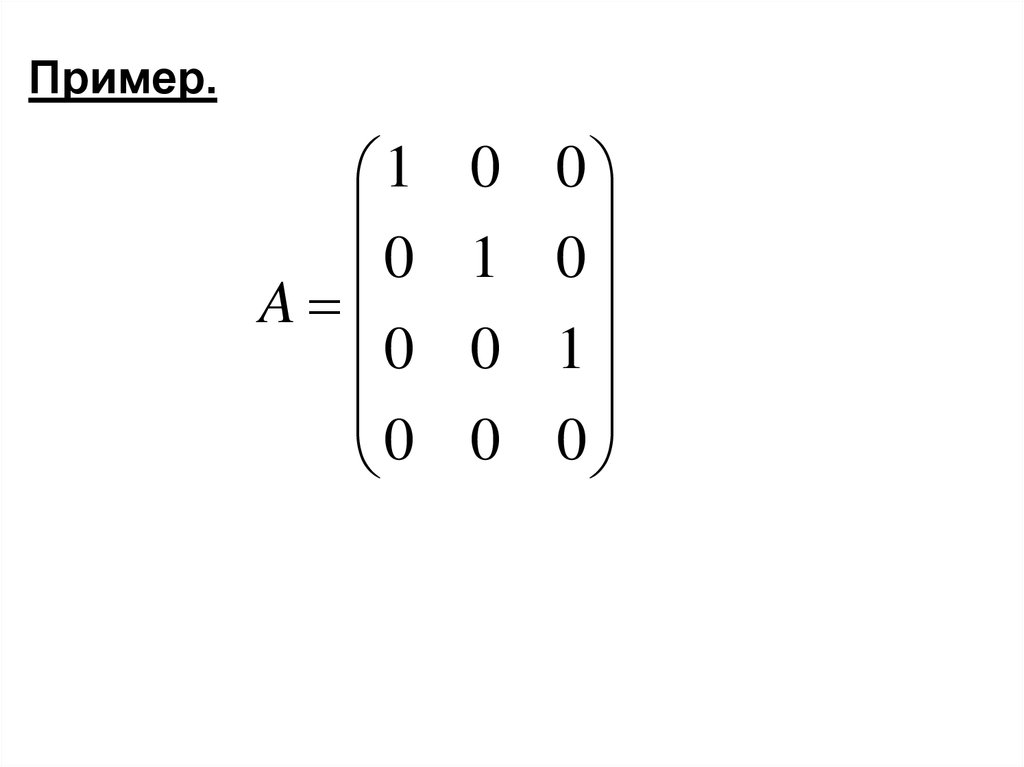
Опр. 4 Матрица имеет вид Гаусса, если1) она ступенчатая
2) все опорные элементы равны
единице
3) над опорными элементами только
нули
23.
Пример.1
0
A
0
0
0 0
1 0
0 1
0 0
24.
Теорема 4 Любая матрица может бытьприведена к ступенчатому виду с
помощью элементарных
преобразований.
Опр. 5 Строки и столбцы матрицы, в
которых расположены ее опорные
элементы, называются базисными.
25.
Опр. 6 Рангом матрицы называетсячисло ненулевых строк в ступенчатом
виде матрицы.
Обозначается
r ( A).
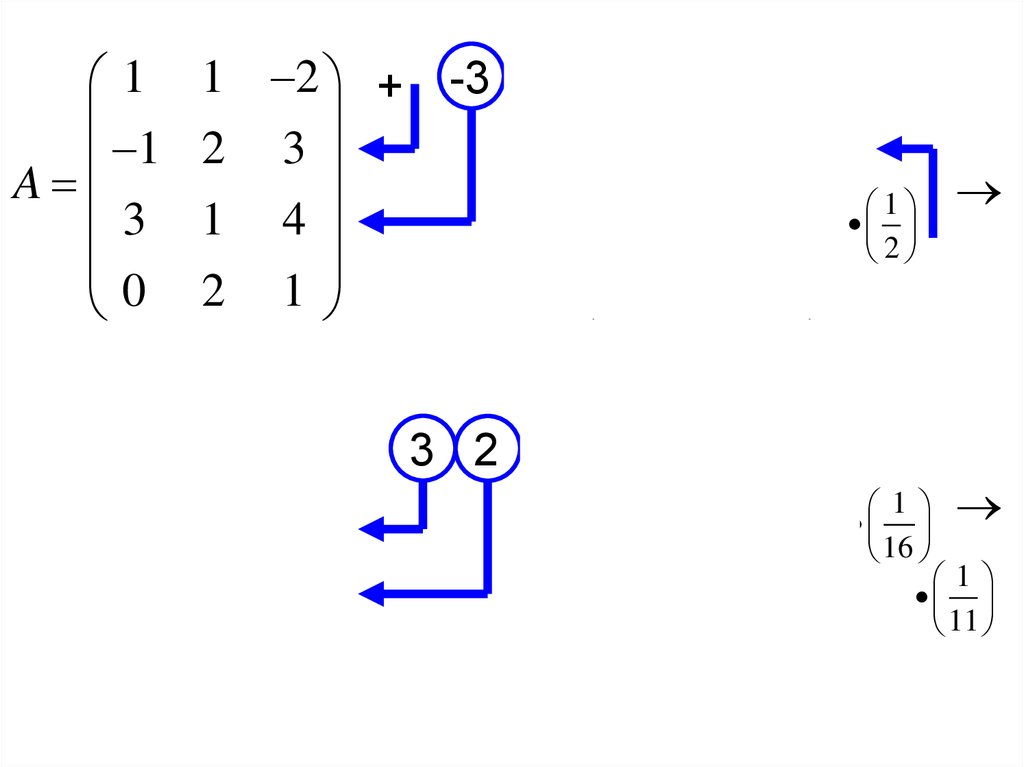
Пример.
Привести матрицу к ступенчатому виду
и найти ранг.
26.
11
A
3
0
1 2 + -3
1 1 2
2 3
0
3
1
0 2 10
1 4
2 1
0 2 1
1 1 2
0
1
5
0 3 1
0 2 1
1
2
1 1 2
3 2
0
1
5
0 0 16 161
1
0 0 11
11
27.
1 1 20
1
5
0 0 1
0 0 1
1 1 2
0 1 5
.
0 0 1
-1
0 0 0
r ( A) 3









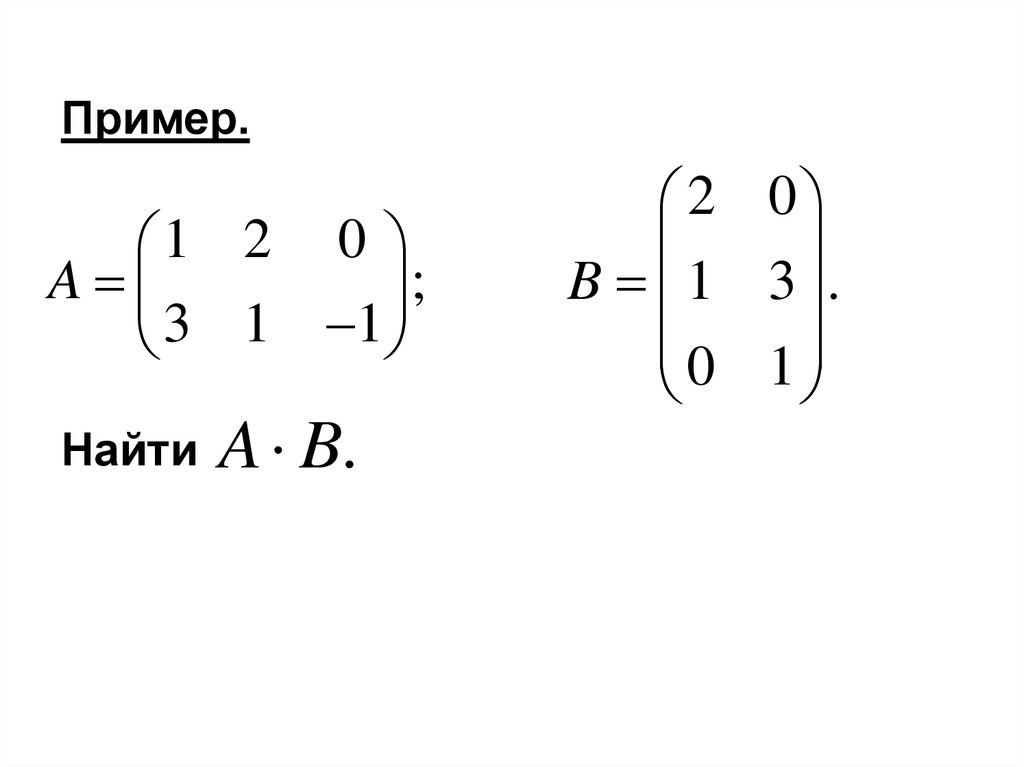
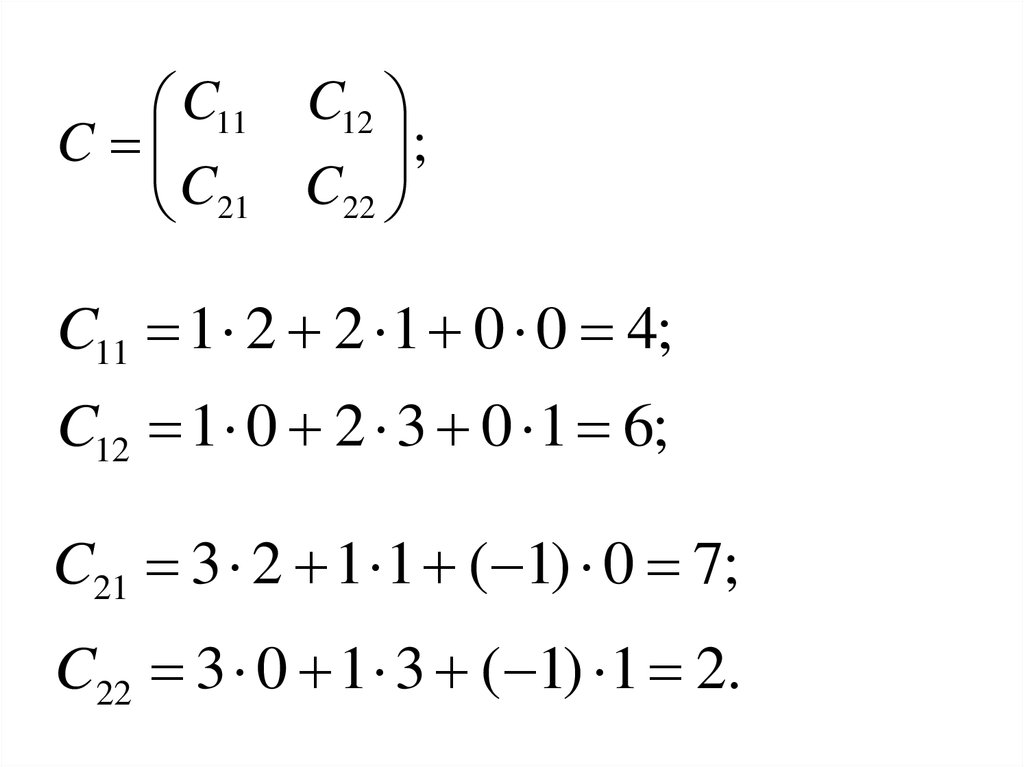









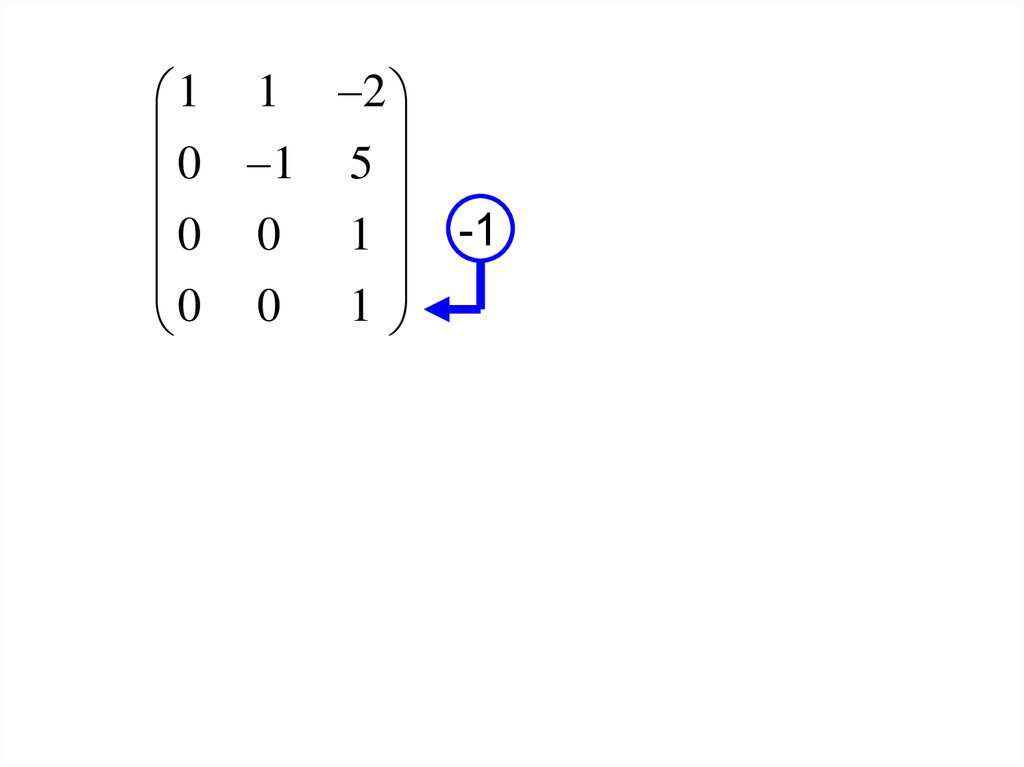
 mathematics
mathematics








