Задача линейной оптимизации

1. «Задача линейной оптимизации»

«ЗАДАЧА ЛИНЕЙНОЙ
ОПТИМИЗАЦИИ»
Цель – смешать три сорта угля А, В, С, чтобы
удовлетворить ограничениям на применение и
минимизировать цену
Задачи:
1.
Составим экономико-математическую модель
задачи
2.
Обозначим количество сорта угля за x1 – Сорт
А, х2 - сорт В, х3 – Сорт С
3.
Найдем цену. Это целевая функция, которую
нужно минимизировать.
4.
Составим нужные функции и определим
ограничения.
5.
Находим решение, обеспечивающее минимум
функции

2. Математическая модель

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Требуется найти значения переменных
x , x ,...., x
1
2
n
соответствующие
минимуму (или максимуму, или константе) целевой функции:
f ( x1 , x2 ,...., xn) c1 x1 c2 x2 cn xn
При m дополнительных ограничениях:
a x
a x
11
1
21
1
a12 x 2 ... a1n
x
a x ... a x
22
2
n
2n
b1
n
b2
…......................................
a x a x ... a x b
c a , b – числовые величины, которые берутся из условия задачи
m1
Где
j,
1
ij
m2
i
2
mn
n
m

3.

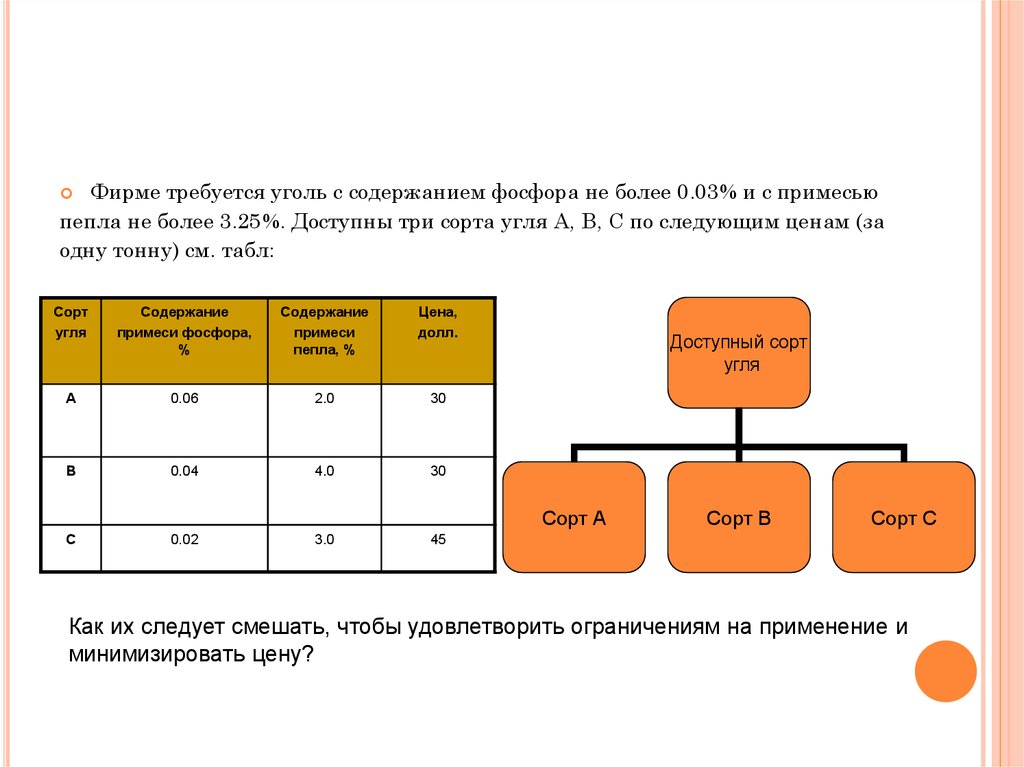
Фирме требуется уголь с содержанием фосфора не более 0.03% и с примесью
пепла не более 3.25%. Доступны три сорта угля А, В, С по следующим ценам (за
одну тонну) см. табл:
Сорт
угля
Содержание
примеси фосфора,
%
Содержание
примеси
пепла, %
Цена,
долл.
А
0.06
2.0
30
В
0.04
4.0
30
С
0.02
3.0
45
Доступный сорт
угля
Сорт А
Сорт В
Сорт С
Как их следует смешать, чтобы удовлетворить ограничениям на применение и
минимизировать цену?

4. Математическая формулировка задачи

МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА
ЗАДАЧИ
x ,x x
Неизвестные –
Целевая функция - f ( x1, x2, x3) 30 x1 30 x2 45 x3
1
2,
3
Система ограничений - x x x 0
0,6 x 0,04 x 0,02 x
2 x 4 x 3x 3,25
1
2
3
1
1
2
2
3
3
0,03

5.

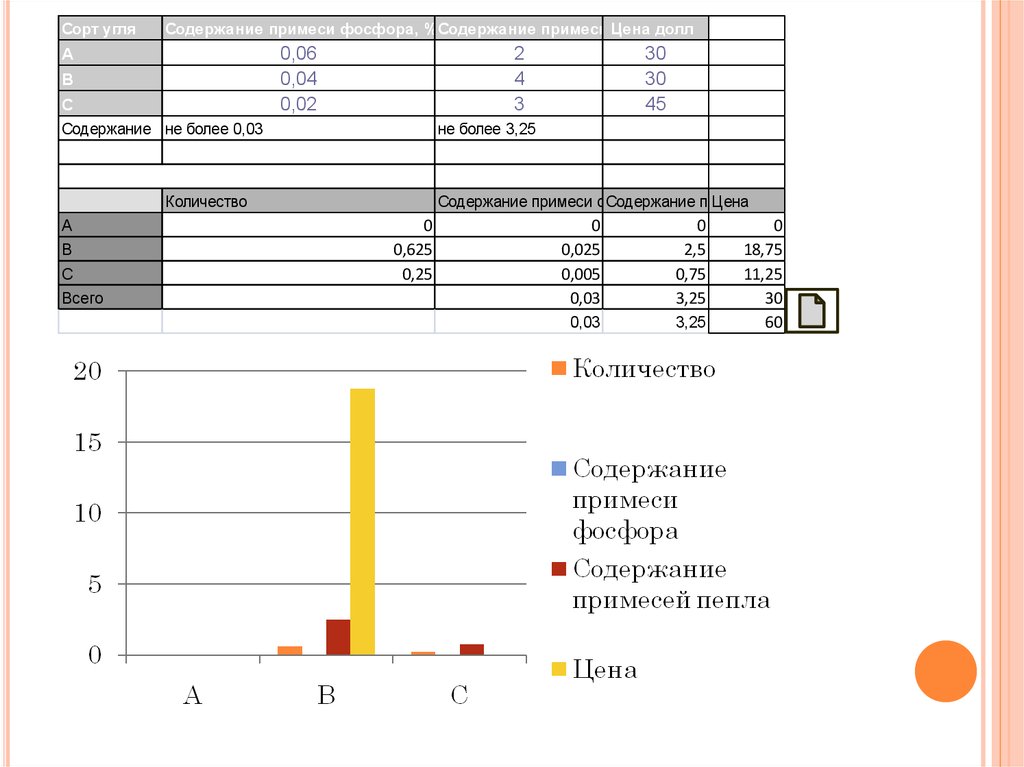
Сорт угля
Содержание примеси фосфора, %Содержание примеси Цена
пепла,
долл
%
А
0,06
0,04
0,02
В
С
2
4
3
Содержание не более 0,03
не более 3,25
Количество
А
В
С
Всего
30
30
45
Содержание примеси фосфора
Содержание примеси
Цена пепла
0
0,625
0,25
0
0,025
0,005
0,03
0
2,5
0,75
3,25
0,03
3,25
0
18,75
11,25
30
60