Similar presentations:
Основы алгоритмизации
1. Основы алгоритмизации
Часть 22.
Разработке алгоритма предшествуют такие этапы, как формализация имоделирование задачи. Формализация предполагает замену словесной
формулировки решаемой задачи краткими символьными обозначениями,
близкими к обозначениям в языках программирования или к
математическим. Моделирование задачи является важнейшим этапом,
целью которого является поиск общей концепции решения. Обычно
моделирование выполняется путем выдвижения гипотез решения задачи и
их проверке любым рациональным способом (прикидочные расчеты,
физическое моделирование и т.д.). Результатом каждой проверки
является либо принятие гипотезы, либо отказ от нее и разработка новой.
3.
При разработке алгоритма используют следующие основные принципы.Принцип поэтапной детализации алгоритма (другое название —
"проектирование сверху-вниз"). Этот принцип предполагает
первоначальную разработку алгоритма в виде укрупненных блоков
(разбиение задачи на подзадачи) и их постепенную детализацию.
Принцип "от главного к второстепенному", предполагающий
составление алгоритма, начиная с главной конструкции. При этом, часто,
приходится "достраивать" алгоритм в обратную сторону, например, от
середины к началу.
Принцип структурирования, т.е. использования только типовых
алгоритмических структур при построении алгоритма.
Говоря о блок-схемах, как о средстве записи алгоритма, можно дать еще
один совет по их разработке. Рекомендуется после внесения исправлений
в блок-схему аккуратно перерисовывать ее с учетом этих исправлений.
Аккуратность записи есть аккуратность мысли программиста. Аккуратно
записанный и детализованный алгоритм упрощает его программирование
и отладку.
4. Рекурсия
Рекурсия (от латинского recursio - возвращение) - это такой способорганизации вычислительного процесса, при котором процедура или
функция в ходе выполнения составляющих ее операторов обращается
сама к себе.
Для того, чтобы такое обращение не было бесконечным, в тексте
подпрограммы должно быть условие, по достижению которого
дальнейшего обращения не происходит.
Рекурсия – это вызов подпрограммы самой себя.
необходимо только понимать, что каждый очередной рекурсивный вызов
приводит к образованию новой копии локальных объектов подпрограммы
и все эти копии, соответствующие цепочке активизированных и не
завершенных рекурсивных вызовов, существуют независимо друг от
друга.
5.
Определение Количество незавершенных копий исходной процедуры,хранящихся в памяти компьютера во время рекурсивных вызовов,
определяет глубину рекурсии.
Рекурсия достаточно широко применяется в программировании, что
основано на рекурсивной природе многих математических алгоритмов. А
также известно, что любой рекурсивный алгоритм можно преобразовать в
эквивалентный итеративный (то есть использующий циклические
конструкции).
В больших и сложных программах иногда приходится заменять рекурсию
на итерацию. Дело в том, что рекурсия связана с многократными
вызовами процедур, а это несколько менее эффективно при выполнении
по сравнению с использованием циклов. Однако рекурсивные версии
программ, как правило, гораздо короче и нагляднее.
6. Алгоритм вычисления числа в ряде Фибоначчи
Вычислите число в ряде Фибоначчи, зная его порядковый номер(нумерация с 1), используя рекурсию (Ряд Фибоначчи, это такой ряд
натуральных чисел, каждый последующий элемент которого
образован суммой двух предыдущих; первые два элемента всегда
равны 1, т.е: 1,1,2,3,5,8,13,21….
7.
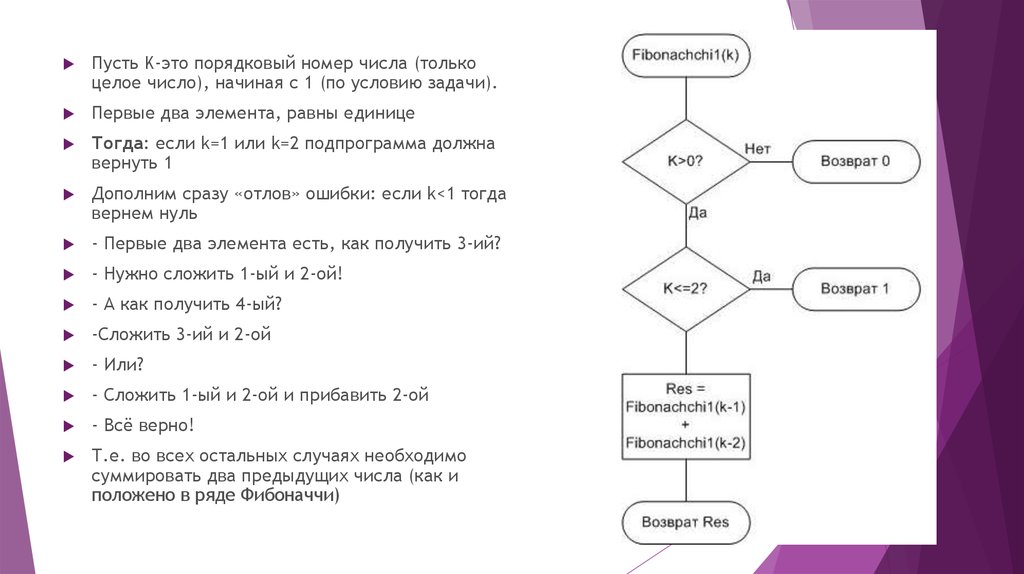
Пусть K-это порядковый номер числа (толькоцелое число), начиная с 1 (по условию задачи).
Первые два элемента, равны единице
Тогда: если k=1 или k=2 подпрограмма должна
вернуть 1
Дополним сразу «отлов» ошибки: если k<1 тогда
вернем нуль
- Первые два элемента есть, как получить 3-ий?
- Нужно сложить 1-ый и 2-ой!
- А как получить 4-ый?
-Сложить 3-ий и 2-ой
- Или?
- Сложить 1-ый и 2-ой и прибавить 2-ой
- Всё верно!
Т.е. во всех остальных случаях необходимо
суммировать два предыдущих числа (как и
положено в ряде Фибоначчи)
8. Чтобы понять насколько это ужасный нерациональный алгоритм, посмотрите сколько операций необходимо сделать машине (ПК), чтобы
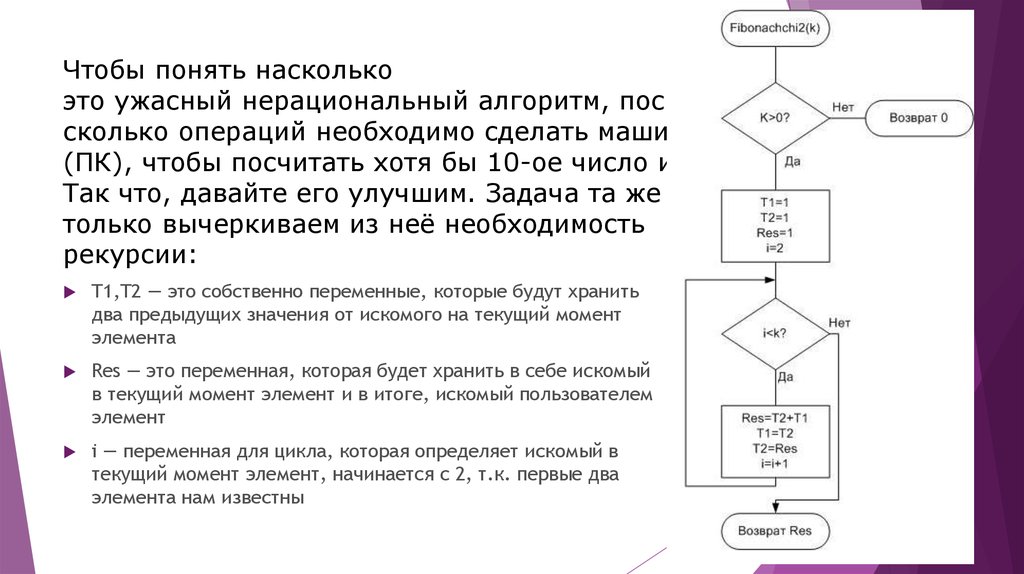
Чтобы понять насколькоэто ужасный нерациональный алгоритм, посмотрите
сколько операций необходимо сделать машине
(ПК), чтобы посчитать хотя бы 10-ое число из ряда.
Так что, давайте его улучшим. Задача та же самая,
только вычеркиваем из неё необходимость
рекурсии:
T1,T2 — это собственно переменные, которые будут хранить
два предыдущих значения от искомого на текущий момент
элемента
Res — это переменная, которая будет хранить в себе искомый
в текущий момент элемент и в итоге, искомый пользователем
элемент
i — переменная для цикла, которая определяет искомый в
текущий момент элемент, начинается с 2, т.к. первые два
элемента нам известны
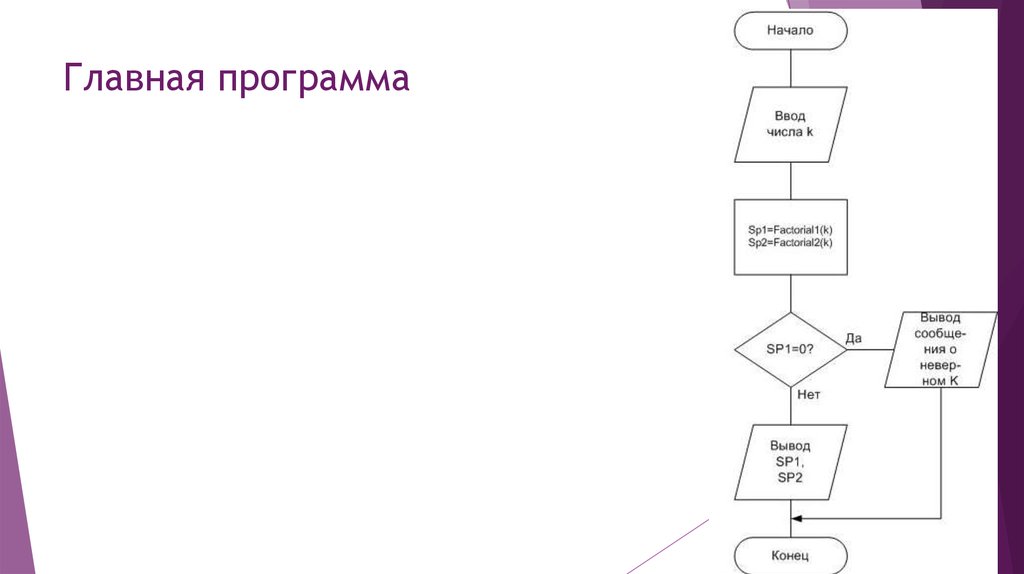
9. Схема главной программы:
10. Алгоритм вычисления факториала
Факториал числа K — это число, которое получится, еслиперемножить все натуральные числа, которые не больше K, но
если K=0, то факториал равен 1; математическая формула
представлена справа
Натуральные числа — это числа, которые являются целыми и не
меньше единицы
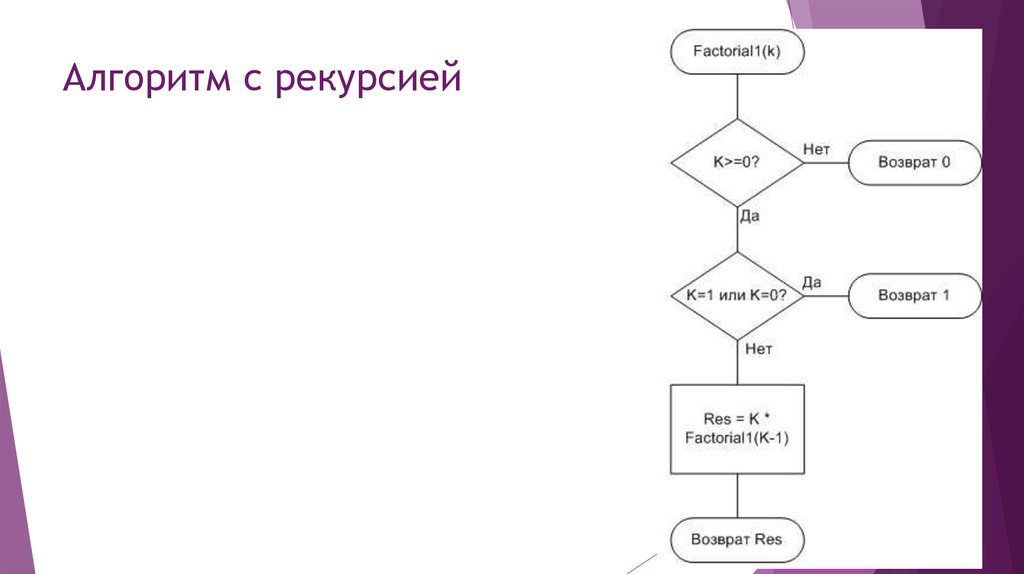
11. Алгоритм с рекурсией
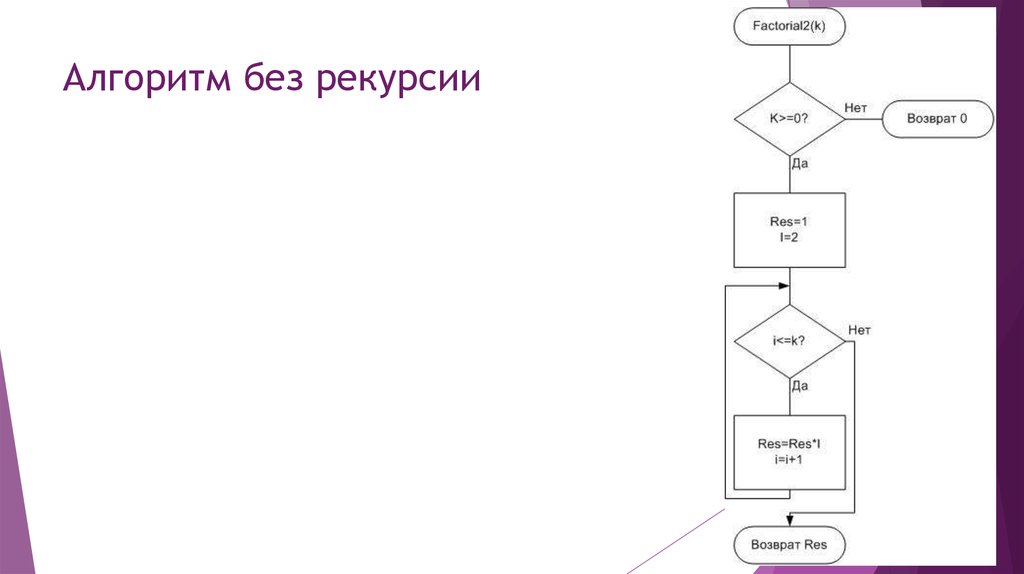
12. Алгоритм без рекурсии
13. Главная программа
14.
В данном случае при вычислении факториала рекурсией значительноувеличивается объем необходимой памяти для вычисления факториала
числа, по сравнению с безрекурсивным алгоритмом, в отличие от
вычисления числа из ряда Фибоначчи, где мы теряли и память и скорость.
Однако, стоит отметить, что идеальным вариантом является
использование цикла, т.к:
— алгоритм требует меньше памяти для выполнения;
— сложность алгоритма не растет в зависимости от K;
— его разработка не занимает намного больше времени, чем написание
простого рекурсивного алгоритма.
15. Псевдокод
Это компактный (зачастую неформальный) язык описания алгоритмов,использующий ключевые слова языков программирования, но опускающий
несущественные подробности и специфический синтаксис
Главная цель использования псевдокода — обеспечить понимание
алгоритма человеком, сделать описание более воспринимаемым, чем
исходный код на языке программирования
16.
Псевдокод занимает промежуточное место между естественным иформальным языками. С одной стороны, он близок к обычному
естественному языку, поэтому алгоритмы могут на нем записываться и
читаться как обычный текст. С другой стороны, в псевдокоде
используются некоторые формальные конструкции и математическая
символика, что приближает запись алгоритма к общепринятой
математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи
команд, присущие формальным языкам, что облегчает запись алгоритма
на стадии его проектирования и дает возможность использовать более
широкий набор команд, рассчитанный на абстрактного исполнителя.
Однако в псевдокоде обычно имеются некоторые конструкции, присущие
формальным языкам, что облегчает переход от записи на псевдокоде к
записи алгоритма на формальном языке. В частности, в псевдокоде, так
же, как и в формальных языках, есть служебные слова, смысл которых
определен раз и навсегда. Они выделяются в печатном тексте жирным
шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует,
поэтому возможны различные псевдокоды, отличающиеся набором
служебных слов и основных (базовых) конструкций.
17. Базовые управляющие структуры псевдокода
18. Общий вид алгоритма:
алг название алгоритма (аргументы и результаты)дано условия применимости алгоритма
надо цель выполнения алгоритма
нач описание промежуточных величин
последовательность команд (тело алгоритма)
кон.
Часть алгоритма от слова алг до слова нач называется заголовком, а
часть, заключённая между словами нач и кон — телом алгоритма.
19.
В предложении алг после названия алгоритма в круглых скобкахуказываются характеристики (арг, рез) и тип значения (цел, вещ,
лог, …) всех входных (аргументы)
и выходных (результаты)переменных.
Примеры предложений алг:
алг
Объем и площадь цилиндра (арг вещ R, H, рез вещ V, S)
алг
Корни КвУр(арг вещ а, b, c, рез вещ x1, x2)
20.
Предложения дано и надо не обязательны.Пример:
алг Сопротивление (арг вещ R1, R2, арг цел N, рез вещ R)
дано | N>5, R1>0, R2>0
надо | R - сопротивление схемы
Здесь в предложениях дано и надо после знака "|"
записаны комментарии. Комментарии можно помещать в конце
любой строки. Они не обрабатываются транслятором, но
существенно облегчают понимание алгоритма.
21.
Оператор присваивания. Служит для вычислениявыражений и присваивания их значений переменным.
Общий вид: А := В, где знак ":=" означает
команду заменить прежнее значение переменной,
стоящей в левой части, на вычисленное значение
выражения, стоящего в правой части.
Например, a:=(b+c)*sin(Pi/4); i:=i+1.
22.
Для ввода и вывода данных используюткоманды
ввод
имена переменных
вывод
имена переменных, выражения, тексты.
23. Пример алгоритма «Hello, world» на псевдокоде
алг HELLOWORLDнач
вывод ('Hello,World')
кон алг HELLOWORLD
24.
Для ветвления применяют команды если и выбор,для организации циклов - команды для и пока.
алг Сумма квадратов (арг цел n, рез цел S)
дано | n > 0
надо | S = 1*1 + 2*2 + 3*3 + ... + n*n
нач цел i
ввод n; S:=0
нц для i от 1 до n
S:=S+i*i
кц
вывод "S = ", S
кон
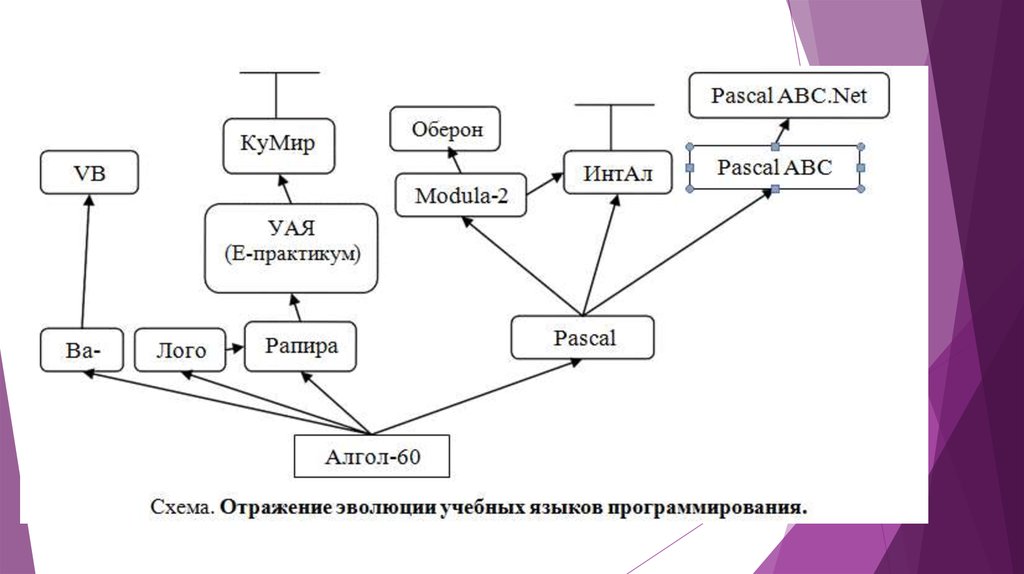
25. Учебные языки программирования
Учебный язык программирования (УЯП) – это язык, предназначенный дляобучения программированию. Главные требования, которым должен
отвечать такой язык, – это простота и универсальность. Чем проще он
будет, тем быстрее его освоит новичок. Универсальность УЯП при
необходимости позволит ученику легко освоить другой ЯП. Возможности
таких языков могут быть ниже, чем возможности полноценных ЯП, но они
и не предназначены для масштабной работы. Однако есть примеры
учебных языков программирования, впоследствии превратившихся в
полноцен- ные, профессионально используемые языки высокого уровня, –
это Паскаль, Бейсик.
26.
27. Золотые правила программирования
1.Не делайте никаких допущений. Не зафиксированные формально
допущения часто служат причиной отказов, особенно с ростом объема
кода.
2.
Чем больше спешки, тем меньше скорость. Всегда думайте, что вы
собираетесь ввести с клавиатуры.
3.
Не верьте никому. Кто угодно, включая вас самих, может сделать ошибки
в логике вашей программы. Ко всем входным и выходным данным
относитесь с подозрением, пока не проверите, что они допустимы.
28.
4.Поймите, кто реально станет читать ваш исходный код: другие
программисты. Пишите с расчетом на них.
Выясните, какие стандарты кода есть для выбранного вами языка, и
освойте каждый из них на практике. Оцените преимущества и недостатки
каждого.
Выберите какой-то один правильный стиль кодирования и
придерживайтесь его постоянно.
29.
5.Учитесь давать объектам прозрачные имена — они должны ясно описывать
то, что за ними скрывается.
6.
Не пишите код, который нуждается во внешней документации. Он
ненадежен. Пишите такой код, который понятен без посторонней
документации.
Пишите код, который может прочесть нормальный человек, причем без
напряжения. Компилятор как-нибудь справится.
7.
Учитесь писать ровно столько комментариев, сколько необходимо.
Отдайте предпочтение качеству, а не количеству.
Не пожалейте труда, чтобы ваш код не требовал поддержки в виде уймы
комментариев.
30.
8.Никогда не пренебрегайте поступающими вам сообщениями об ошибках.
Если существует канал для сообщений об ошибках, значит, для этого есть
причины.
9.
Изучите свои стандартные инструменты вдоль и поперек. Время, которое
вы потратите на их изучение, незамедлительно окупится.
10.
Тестирование может вскрыть только наличие ошибок. Оно не может
доказать отсутствие неисправностей. Не поддавайтесь ложному чувству
спокойствия, если код прошел ряд неадекватных тестов.
Тестируйте каждый написанный вами фрагмент кода. Не рассчитывайте,
что кто-то другой сделает это за вас.
31.
11.Об эффективности работы программы нужно думать с самого начала — не
надейтесь, что в конце разработки вам удастся повысить ее ценой
небольших изменений.
Корректность кода гораздо важнее его скорости. Что толку быстро
получить результат, если он неверный!
12.
Оценка длительности разработки программного продукта представляет
собой основанную на фактах догадку. Для каждой оценки есть некоторая
мера вашей уверенности в ней.
Оценка времени разработки программ представляет собой действительно
трудную задачу. Избегайте недооценки объема предстоящей работы.
Учтите возможные последствия неправильной оценки.

























 programming
programming








