11_Рекурсия

1. Преподаватель Мельникова Татьяна Федоровна Тема : Рекурсивные методы

Основы алгоритмизации и программирования

2. рекурсия

“Итерация – от человека,
а рекурсия – от бога”

3. Примеры рекурсии

В окружающем нас мире часто можно встретить
объекты, обладающие самоподобием.
То есть часть большого объекта в чем-то
сходна с самим объектом.
Рекурсивным называется объект, частично
состоящий или определяемый с помощью самого
себя.
Слово «рекурсия» происходит от латинского
слова «recursio» - возвращение.

4. Виды рекурсии

Определение: Если подпрограмма обращается сама к себе как
к подпрограмме непосредственно или через цепочку
подпрограмм, то этот цепочка обращений называется
рекурсией.
Если некоторая процедура Р содержит явную ссылку на саму
себя, то ее называют прямо рекурсивной,
если же Р ссылается на другую процедуру В, содержащую
ссылку на Р, то Р называют косвенно рекурсивной.

5. Прямая рекурсия

«А не зациклится ли, то есть, не будет ли
бесконечно выполняться рекурсивная
программа?»
Опасность зацикливания вполне реальна.
Например, стихотворение
"У попа была собака" может повторяться до
бесконечности.
А со считалкой про 10 негритят дело обстоит иначе.

6. текст стихотворения:

«10 негритят пошли купаться в море,
10 негритят резвились на просторе,
Один из них пропал и вот вам результат:
9 негритят пошли купаться в море,
9 негритят резвились на просторе,
Один из них пропал – и вот вам результат:
…
1 (из) негритят пошли(ел) купаться в море,
1 (из) негритят резвились(ся)на просторе,
Один из них пропал – и вот вам результат:
Нет больше негритят!»

7. решение

Первые три строчки этого стихотворения повторяются
10 раз с небольшим изменением – число негритят
уменьшается с каждым разом на единицу.
И только когда число негритят уменьшилось до нуля,
стихотворение заканчивается единственной строчкой
«Нет больше негритят!».
Напишите процедуру про негритят

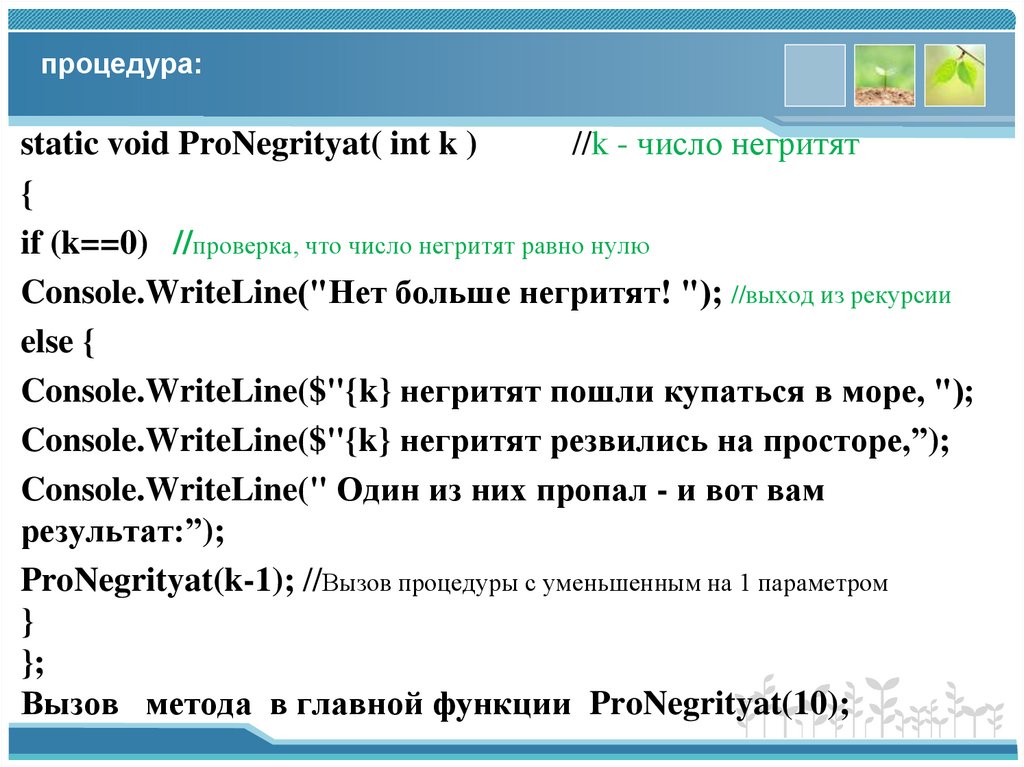
8. процедура:

static void ProNegrityat( int k )
//k - число негритят
{
if (k==0) //проверка, что число негритят равно нулю
Console.WriteLine("Нет больше негритят! "); //выход из рекурсии
else {
Console.WriteLine($"{k} негритят пошли купаться в море, ");
Console.WriteLine($"{k} негритят резвились на просторе,”);
Console.WriteLine(" Один из них пропал - и вот вам
результат:”);
ProNegrityat(k-1); //Вызов процедуры с уменьшенным на 1 параметром
}
};
Вызов метода в главной функции ProNegrityat(10);

9. Прямая рекурсия

При обращении подпрограммы к самой себе происходит то же
самое, что и при обращении к любой процедуре или функции:
в стек записывается адрес возврата, резервируется место
под локальные переменные, происходит передача
параметров, после чего управление передается первому
исполняемому оператору программы.
При повторном вызове этот процесс повторяется.
Число копий переменных, одновременно находящихся в
стековой памяти, называется глубиной рекурсии.
Для завершения рекурсивных вызовов в рекурсивной
подпрограмме обязательно должно быть условие выхода из
нее, заканчивающееся возвратом в вызывающую программу.

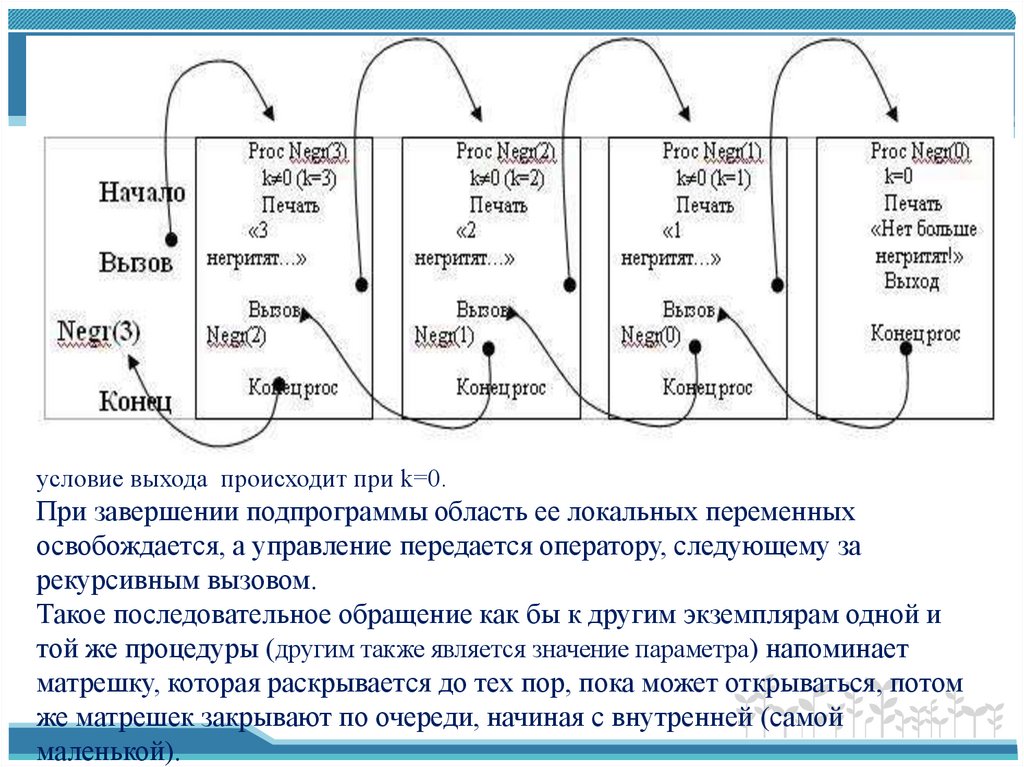
10.

условие выхода происходит при k=0.
При завершении подпрограммы область ее локальных переменных
освобождается, а управление передается оператору, следующему за
рекурсивным вызовом.
Такое последовательное обращение как бы к другим экземплярам одной и
той же процедуры (другим также является значение параметра) напоминает
матрешку, которая раскрывается до тех пор, пока может открываться, потом
же матрешек закрывают по очереди, начиная с внутренней (самой
маленькой).

11. Рекурсивные методы

Для решения задач рекурсивными методами
разрабатывают следующие этапы, образующие
рекурсивную триаду:
параметризация – выделяют параметры, которые
используются для описания условия задачи, а затем
в решении;
база рекурсии – определяют тривиальный случай,
при котором решение очевидно, то есть не требуется
обращение функции к себе;
декомпозиция – выражают общий случай через
более
простые
подзадачи
с
измененными
параметрами.

12. Выводы:

1) Рекурсивная подпрограмма должна иметь условие выхода,
чтобы не быть бесконечной. Поэтому в первую очередь надо
оформлять выход из рекурсии.
2) Рекурсия не может иметь слишком много вложений.
Ограничение по стековой памяти, которое не может превышать
64 Кб.
Для каждого текущего обращения формируется локальный
слой данных стека (при этом совпадающие идентификаторы разных
слоев стека независимы друг от друга и не отождествляются).
Завершение вычислений происходит посредством
восстановления значений данных каждого слоя в порядке,
обратном рекурсивным обращениям.

13. Пример

static void Rec(int a)
{
if (a>0)
Rec(a-1);
Console.WriteLine(a);
}
что произойдет, если в основной программе поставить вызов,
например, вида Rec(3).

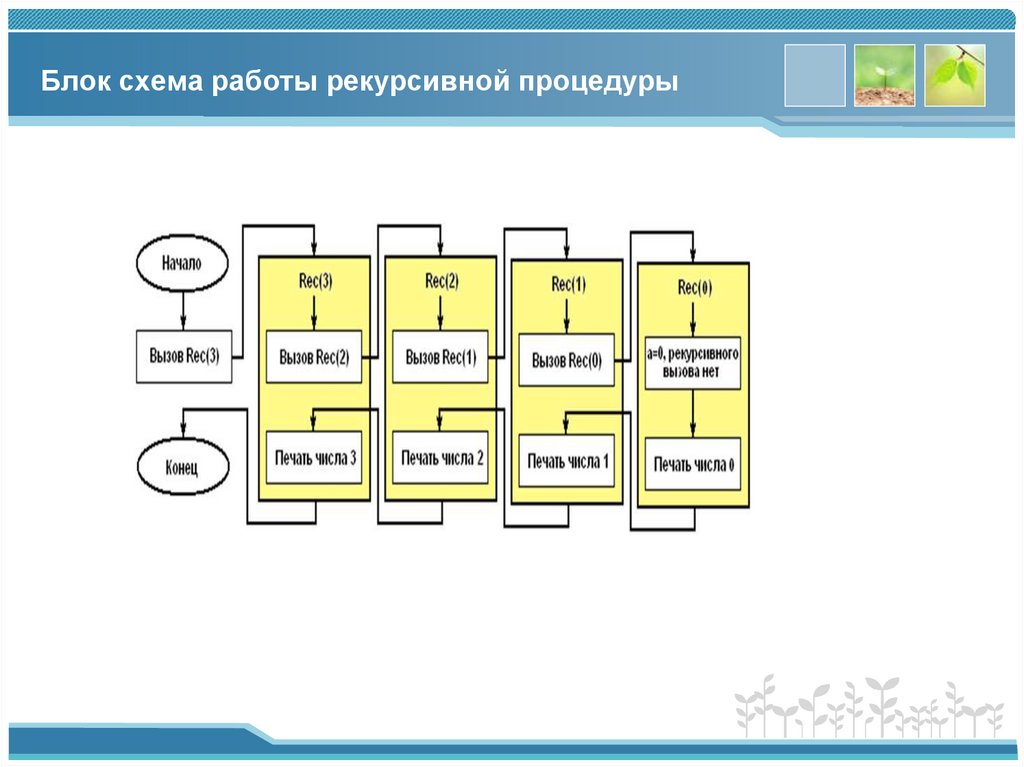
14. работа рекурсивной процедуры

Процедура Rec вызывается с параметром a = 3.
В ней содержится вызов процедуры Rec с параметром a = 2.
Предыдущий вызов еще не завершился, поэтому можете
представить себе, что создается еще одна процедура и до
окончания ее работы первая свою работу не заканчивает.
Процесс вызова заканчивается, когда параметр a = 0.
В этот момент одновременно выполняются 4 экземпляра
процедуры
Четвертая вызванная процедура (Rec(0)) напечатает число 0 и
закончит свою работу. После этого управление возвращается к
процедуре, которая ее вызвала (Rec(1)) и печатается число 1. И
так далее пока не завершатся все процедуры.
Результатом вызова будет печать четырех чисел: 0, 1, 2, 3.

15. Блок схема работы рекурсивной процедуры

16. Факториал

Хорошей иллюстрацией механизма рекурсии является функция
для вычисления факториала натурального числа.
Факториал вычисляется следующим образом:
N! = 1 * 2 * 3 * … * (N-1) * N,
(1)
то есть представляет собой произведение натуральных чисел от
1 до N включительно.
На эту функцию можно посмотреть и под другим углом зрения.
Формулу (1), мы можем представить так:
N! = N * (N-1)!
(2)

17. Факториал вычисляется

Таким образом, при определении факториала через сам
факториал! можно переходить к бесконечному циклу.
Однако это впечатление обманчиво, потому что на самом деле
факториал N определяется через факториал (N-1), то есть
нахождение неизвестной функции сводится к вычислению той
же неизвестной функции от другого аргумента, на единицу
меньшего, чем исходный.
Окончательно разорвать замкнутый круг сможем, если
дополним рекурсивное определение (2) еще одним, которое
служит чем-то вроде тупика, предназначенного для остановки
процесса:
0! = 1
(3)

18. Пример

Правила (2) и (3) совместно позволяют вычислить
значение факториала от любого аргумента.
Рассмотрим для примера вычисление значение 5!,
несколько раз применив правило (2) и однократно –
правило (3):
5! → 5 * 4! → 5 * 4 * 3! → 5 * 4 * 3 * 2! →
→ 5 * 4 * 3 * 2 * 1! → 5 * 4 * 3 * 2 * 1
Мы получили результат, который совпадает с
определением (1) с точностью до перестановки
сомножителей.

19. Пример

{
static long Fact(int n) //рекурсивный метод
{
if (n==0 || n==1)
return 1;
//нерекурсивная ветвь
else return n*Fact(n-1); //шаг рекурсии -
повторный вызов метода с другим параметром
}
static void Main()
{
Console.Write("n=");
int n =int.Parse( Console.ReadLine());
long f=Fact(n); // вызов метода F
Console.WriteLine("{0}!={1}",n, f);
}
}

20. Процесс выполнения рекурсивного алгоритма

21. Вывод

Рекурсия связана с многократными вызовами функции,
а это несколько менее эффективно при выполнении по
сравнению с использованием цикла.
К тому же требует больше памяти.
Однако рекурсивные версии программ, как правило,
гораздо короче и нагляднее, не требуют наличия цикла
и параметра цикла.
Резюме: Итерация требует меньше места в памяти
и машинного времени, чем рекурсия, которой
необходимы затраты на управление стеком.
Если для некоторой задачи возможны два решения,
предпочтение следует отдать итерации

22. Задачи

1 Вычислить количество цифр в заданном натуральном числе a.
2 Вычислить степень числа
3 Вывод всех делителей натурального числа

23. Спасибо за внимание!