Similar presentations:
Интерактивная компьютерная графика. Часть 5-1 (Проекции и нормали)
1. (проекции и нормали)
Часть 5-1(проекции и нормали)
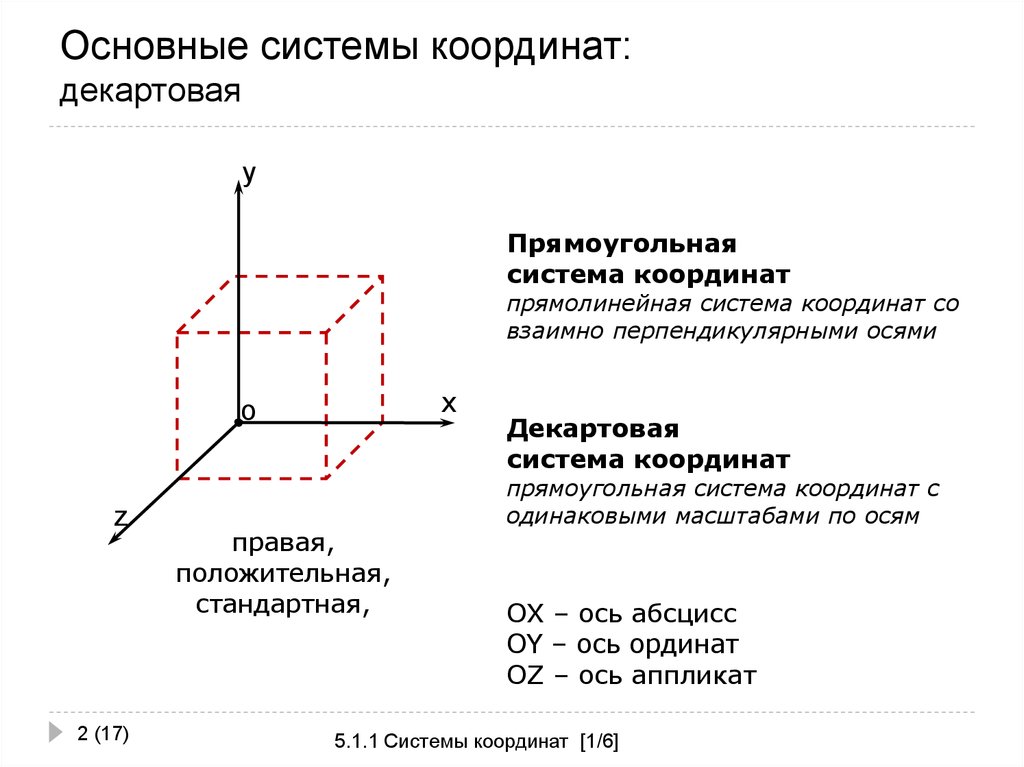
2. Основные системы координат: декартовая
yПрямоугольная
система координат
прямолинейная система координат со
взаимно перпендикулярными осями
x
o
z
2 (17)
правая,
положительная,
стандартная,
Декартовая
система координат
прямоугольная система координат с
одинаковыми масштабами по осям
OX – ось абсцисс
OY – ось ординат
OZ – ось аппликат
5.1.1 Системы координат [1/6]
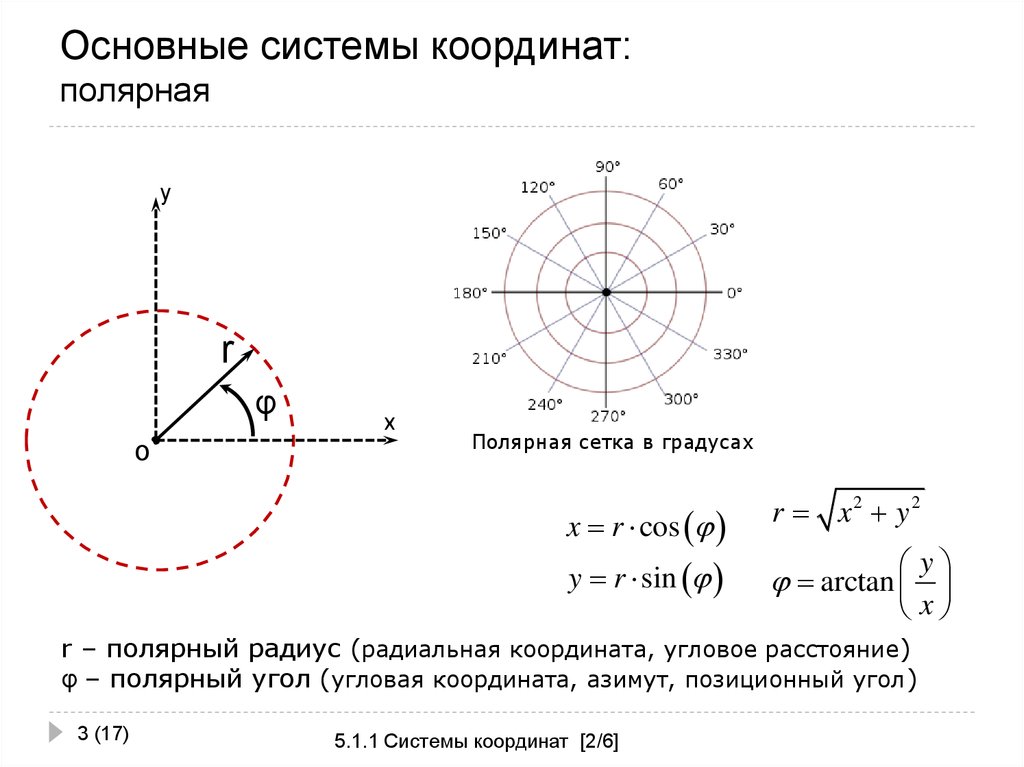
3. Основные системы координат: полярная
yr
φ
o
x
Полярная сетка в градусах
x r cos
r x2 y 2
y r sin
arctan
x
y
r – полярный радиус (радиальная координата, угловое расстояние)
φ – полярный угол (угловая координата, азимут, позиционный угол)
3 (17)
5.1.1 Системы координат [2/6]
4. Основные системы координат: цилиндрическая
zo
z
r φ
x
r
x r cos
y r sin
z z
4 (17)
r x2 y 2
y
arctan
x
z z
5.1.1 Системы координат [3/6]
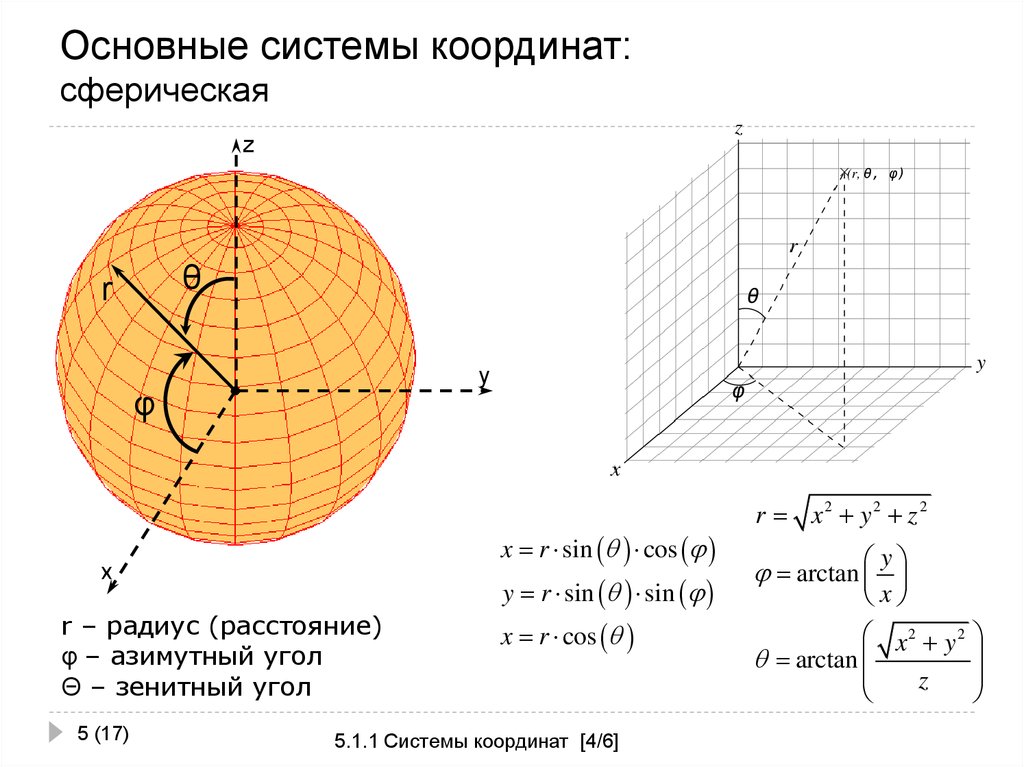
5. Основные системы координат: сферическая
zθ
r
y
φ
x r sin cos
x
r – радиус (расстояние)
φ – азимутный угол
Θ – зенитный угол
5 (17)
y r sin sin
x r cos
5.1.1 Системы координат [4/6]
r x2 y 2 z 2
y
arctan
x
x2 y 2
arctan
z
6. Дополнительные системы координат
Аффинная (косоугольная) система координатБарицентрические координаты
Биангулярные координаты
Биполярные координаты
Бицентрические координаты
Бицилиндрические координаты
Конические координаты
Координаты Риндлера
Параболические координаты
Проективные координаты
Тороидальная система координат
Трилинейные координаты
Цилиндрические параболические координаты
Эллипсоидальные координаты
6 (17)
5.1.1 Системы координат [5/6]
7. Системы координат: (правило буравчика)
OYOY
OX
Правосторонняя
система OZ
координат
OZ
OX
OY
OX
7 (17)
OZ
5.1.1 Системы координат [6/6]
Левосторонняя
система
координат
8. Векторное произведение
Вектор c являетсявекторным произведением
векторов a и b, если
(c,a)=(c,b)=0
и
|c|=|a|∙|b|∙sin(a,b)
(длина c равна площади параллелограмма,
построенного на векторах a и b)
i
j
c a, b a b a x
ay
bx
by
8 (17)
Правая тройка,
Правило правой руки
a y bz a z by
a z a z bx a x bz
bz a x by a y bx
k
5.1.2 Вычисление нормали [1/4]
9. Вычисление нормали в вершине: для грани
a a x , a y , a zb bx , by , bz
n
c c x , c y , c z
По правилу правой руки:
n (c a) (b a)
b
По правилу левой руки:
n (b a) (c a)
a
c
9 (17)
5.1.2 Вычисление нормали [2/4]
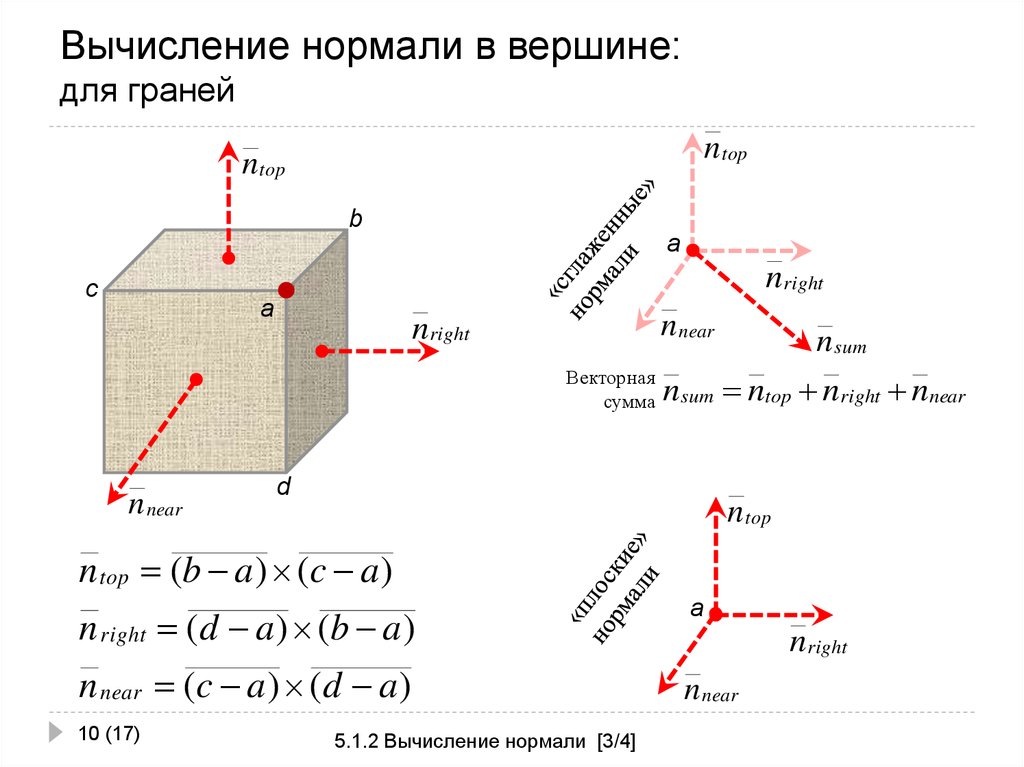
10. Вычисление нормали в вершине: для граней
ntopntop
b
a
nright
c
a
n near
nright
Векторная
сумма
n near
n sum
nsum ntop nright nnear
d
ntop
n top (b a ) (c a )
n right ( d a ) (b a )
n near (c a ) (d a )
10 (17)
5.1.2 Вычисление нормали [3/4]
a
nright
n near
11. Задание нормали в вершине
Задание вектора нормали vnormal=(x,y,z)T:glNormal3f( x, y, z )
glNormal3fv ( veс_normal )
Указание на автоматическую принудительную
нормализацию
(установление единичной длины) векторов нормалей:
glEnable ( GL_NORMALIZE )
Вектор нормали является таким же атрибутом вершины, как и цвет,
и может задаваться внутри блока glBegin / glEnd
При использовании целочисленных нормалей (glNormal3i(*) и т.п.)
значение вектора автоматически масштабируется в диапазон [-1,1]
11 (17)
5.1.2 Вычисление нормали [4/4]
12. Типы проекций
Плоские геометрические проекцииЛинии параллельны?
Нет точки схода?
Параллельная
Ортогональные
Видовые:
- спереди
- сбоку
- сверху
Оси
перпенди
кулярны
картинной
плоскости?
Направление
проецирования
перпендикулярно
картинной
плоскости?
Аксонометрическая
Изометрическая
Одноточечная
Косоугольные
Двухточечная
Кабине (cabinet)
Кабинетная перспектива
Фронтальная диметрия
Кавалье (cavalier)
Военная перспектива
Горизонтальная изометрия
Диметрическая
12 (17)
Центральная (перспективная)
5.1.3 Типы проекций [1/6]
Трехточечная
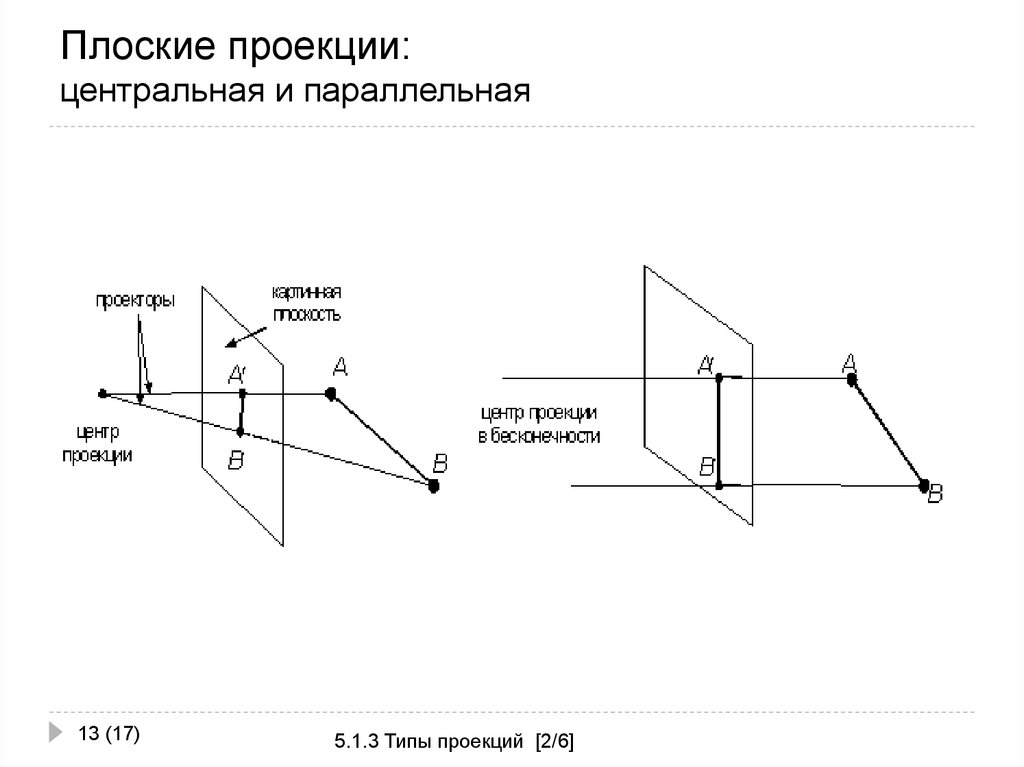
13. Плоские проекции: центральная и параллельная
13 (17)5.1.3 Типы проекций [2/6]
14. Параллельные проекции: ортогональные и косоугольные
14 (17)5.1.3 Типы проекций [3/6]
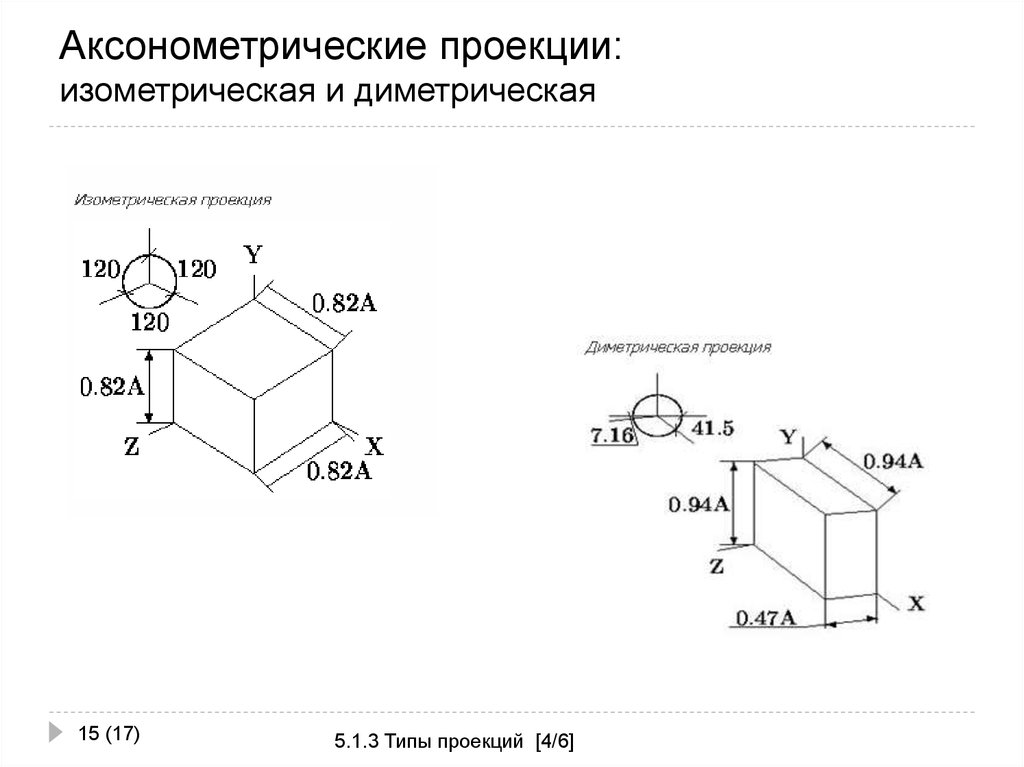
15. Аксонометрические проекции: изометрическая и диметрическая
15 (17)5.1.3 Типы проекций [4/6]
16. Косоугольные проекции: военная и кабинетная
Свободная проекция(аксонометрическая косоугольная
горизонтальная изометрическая проекция)
16 (17)
5.1.3 Типы проекций [5/6]
Кабинетная проекция
(аксонометрическая косоугольная
фронтальная диметрическая проекция)
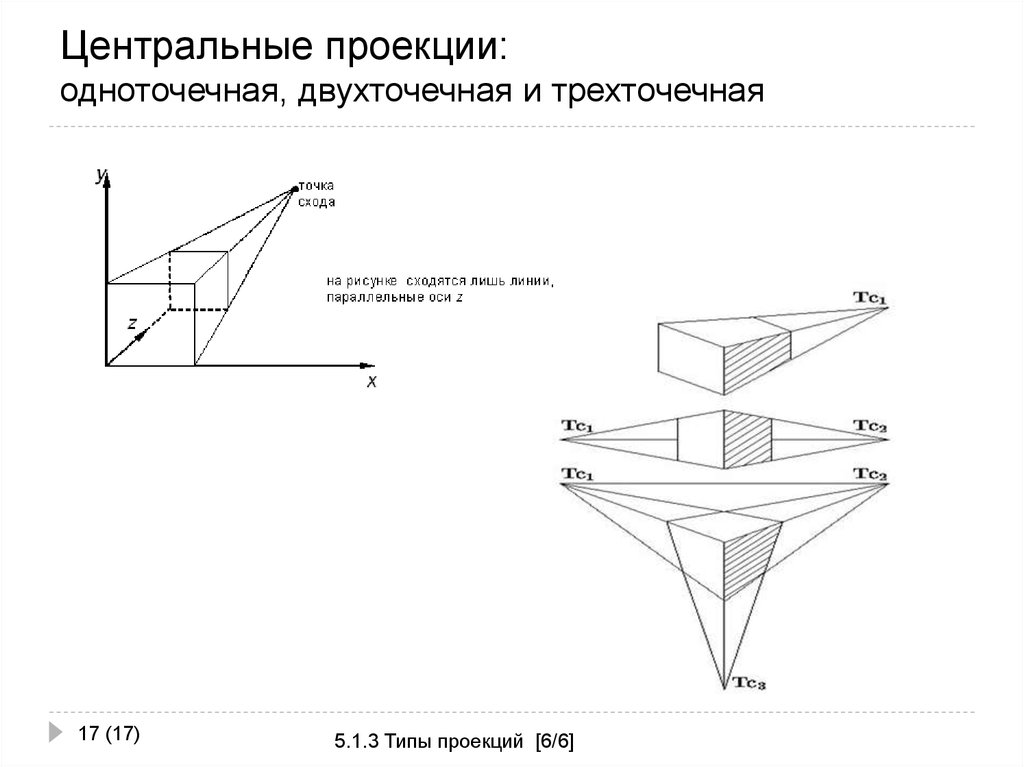
17. Центральные проекции: одноточечная, двухточечная и трехточечная
17 (17)5.1.3 Типы проекций [6/6]










 drafting
drafting








