Введение в начертательную геометрию. Теория параметризации. (Лекция 1)

1.

Кафедра инженерной геометрии,
компьютерной графики и
автоматизированного проектирования
Лекция №1
Введение в начертательную
геометрию
Теория параметризации
Разработчик: проф. Тюрина Валерия Александровна

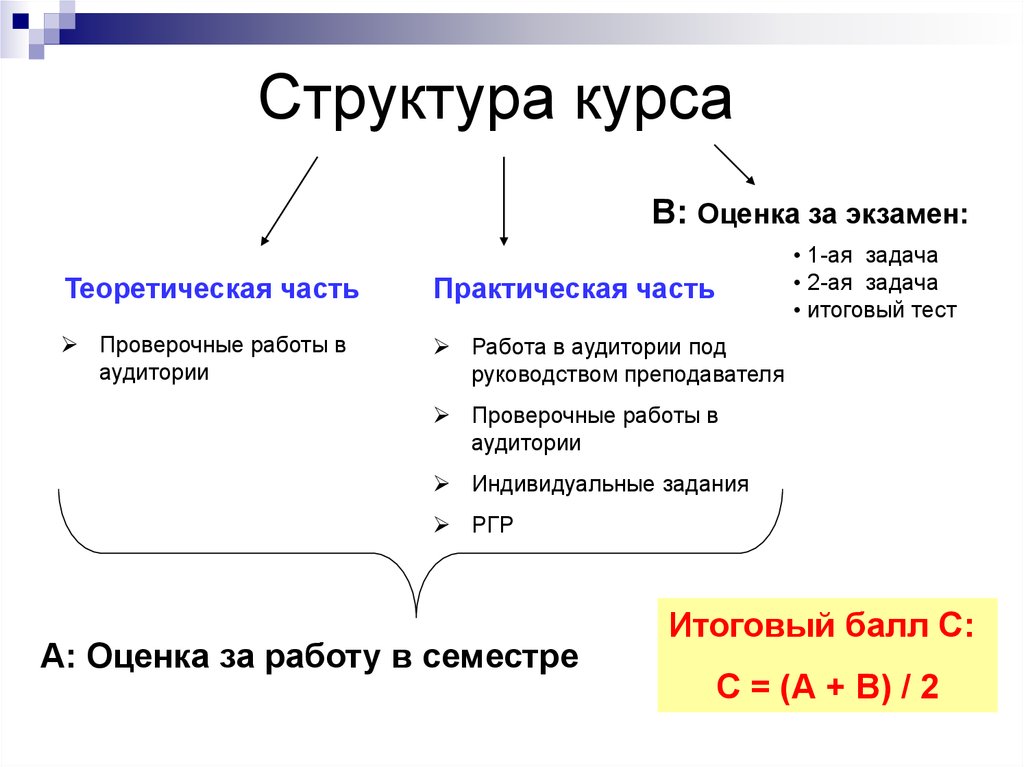
2. Структура курса

В: Оценка за экзамен:
• 1-ая задача
• 2-ая задача
• итоговый тест
Теоретическая часть
Практическая часть
Проверочные работы в
аудитории
Работа в аудитории под
руководством преподавателя
Проверочные работы в
аудитории
Индивидуальные задания
РГР
А: Оценка за работу в семестре
Итоговый балл С:
С = (А + В) / 2

3. «Что необходимо на занятии?»

1.
2.
3.
4.
5.
6.
7.
8.
Учебник (несколько, взять в библиотеке)
Задачник (авторы: Мошкова Т.В., Тюрина В.А.)
Линейки, «треугольники»
Циркуль
Карандаши (твердые и мягкие)
Тетрадь формата А4
Ватман (А4, А3)
«Флэшка»

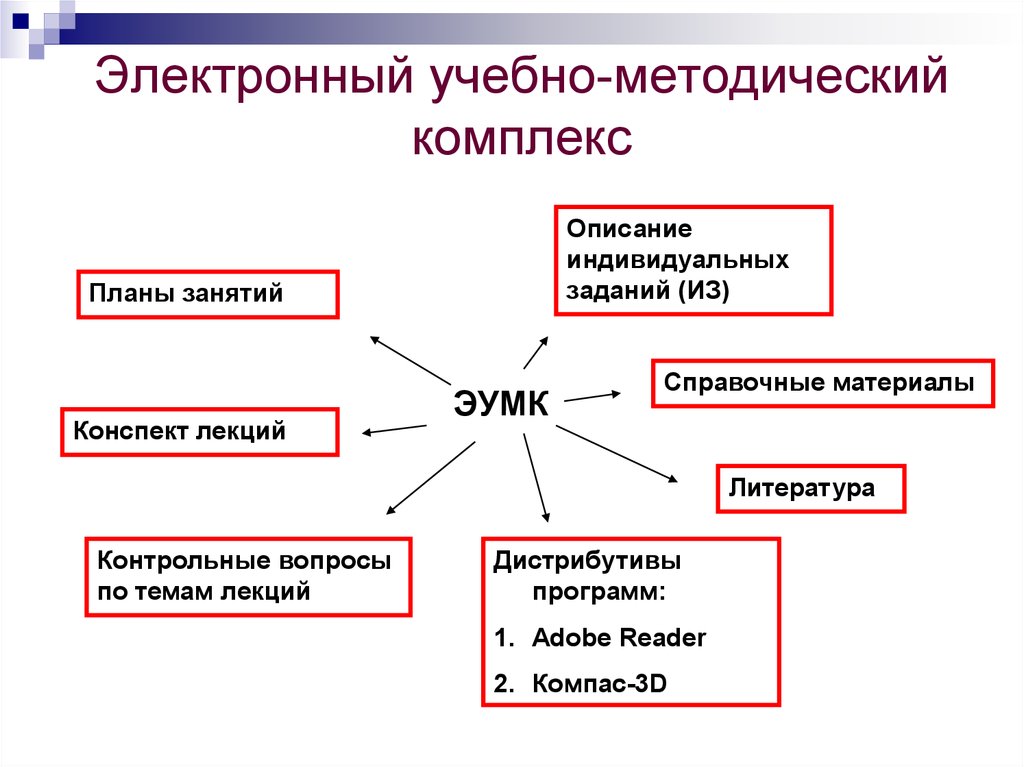
4. Электронный учебно-методический комплекс

Описание
индивидуальных
заданий (ИЗ)
Планы занятий
Конспект лекций
ЭУМК
Справочные материалы
Литература
Контрольные вопросы
по темам лекций
Дистрибутивы
программ:
1. Adobe Reader
2. Компас-3D

5. Место НГ в системе наук

Естественные науки
Математика
Место НГ
в системе наук
Геометрия
…
Фундаментальная научная
основа будущей профессии!
…
Начертательная
геометрия

6. Начертательная геометрия – это раздел геометрии, в котором изучаются :

Методы построения плоских изображений
пространственных геометрических объектов
Способы решения пространственных
геометрических задач на этих изображениях

7. Геометрическая модель (фигура) – носитель геометрической информации об объекте:

учитывает только форму, размеры и
расположение предметов;
не учитывает их физических и иных
свойств (например, материал, массу,
прочность, цвет и т.п.)

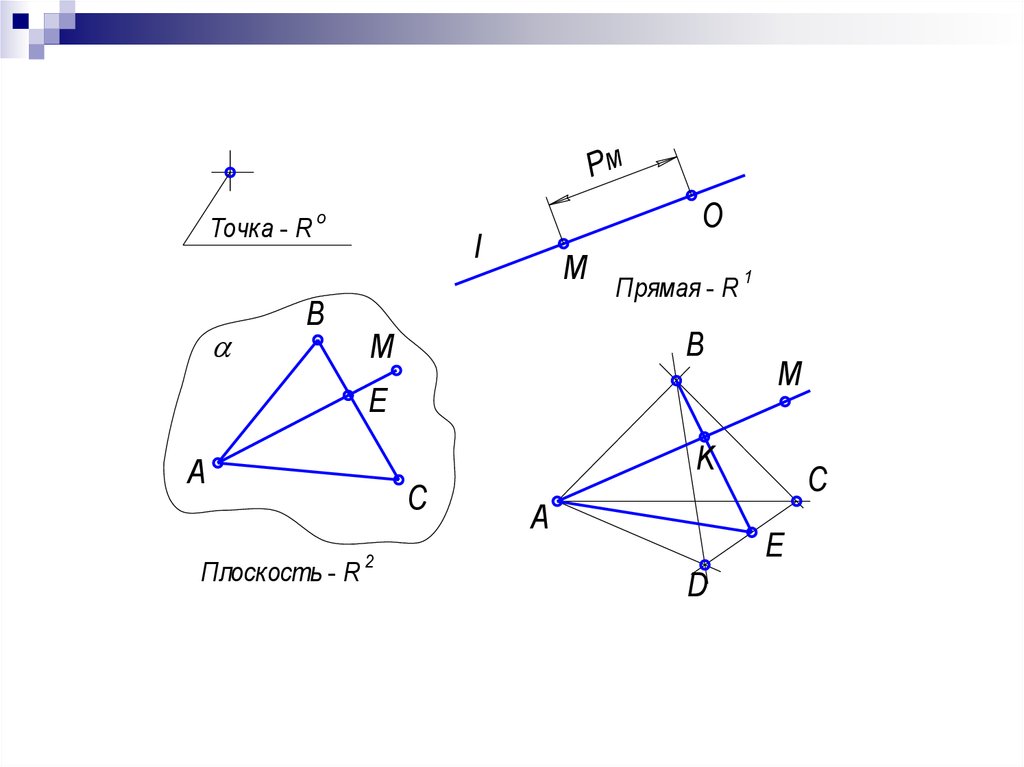
8. Базовые геометрические фигуры НГ, не имеющие формы:

Точка - нольмерное пространство R0
Прямая - одномерное пространство R1
Плоскость - двумерное пространство R2

9. Математическая модель окружающего нас пространства – линейное 3-х мерное пространство R3, базовый элемент которого – точка.

Геометрическую фигуру Ф считают
состоящей из точек и определяют как
некоторое множество точек U.
U R3

10. Геометрические фигуры делятся на:

Линейные фигуры
(точка, прямая, плоскость)
Нелинейные
(кривая линия, поверхность)
Составные
(например, многогранник)

11. Виды изображений

Можно судить об объекте по его
изображению, если оно обладает
следующими свойствами:
Обратимость
Наглядность
Единство условностей

12. Обратимость

Свойство, позволяющее однозначно
восстанавливать действительную форму и
размеры предмета, а также его положение в
пространстве.
Графическое изображение, обладающее
свойством обратимости, называется
чертежом.

13. Наглядность

Свойство изображения, дающее
возможность вызвать в мозгу зрителя
пространственное представление о
предмете.
Элемент наглядности – естественность (особенно
важен для архитектурно-строительной практики).
Желателен для чертежа.

14. Единство условностей

Принятые при выполнении изображения
условности должны быть общими для
специалистов определенной области знаний.
Установлены законы оформления чертежей –
стандарты (ГОСТ).
Свод таких стандартов называют Единой
Системой Конструкторской Документации
(ЕСКД).

15. ЕСКД в общей системе стандартизации

ЕСКД присвоен код 2.
Внутри ЕСКД стандарты объединяются по группам,
которым присваивается код от 0 до 9.
Например, 3 – общие правила выполнения чертежей.
В каждой группе стандартам присваивается
порядковый номер, затем указывается год
регистрации стандарта и присваивается
наименование.
Например,
ГОСТ 2.301-68 Форматы.

16. Изображение, самое близкое к естественному, перспектива

Эскиз архитектурно-перспективной декорации.
Художник П. Гонзаго. Начало XIX века

17. Перекресток ул. Б. Покровской и ул. Грузинской

18. Изображение, выполняемое с некоторыми условностями, также обладающее высокой наглядностью, аксонометрия

19. Изображение, выполняемое с некоторыми условностями, технический чертеж

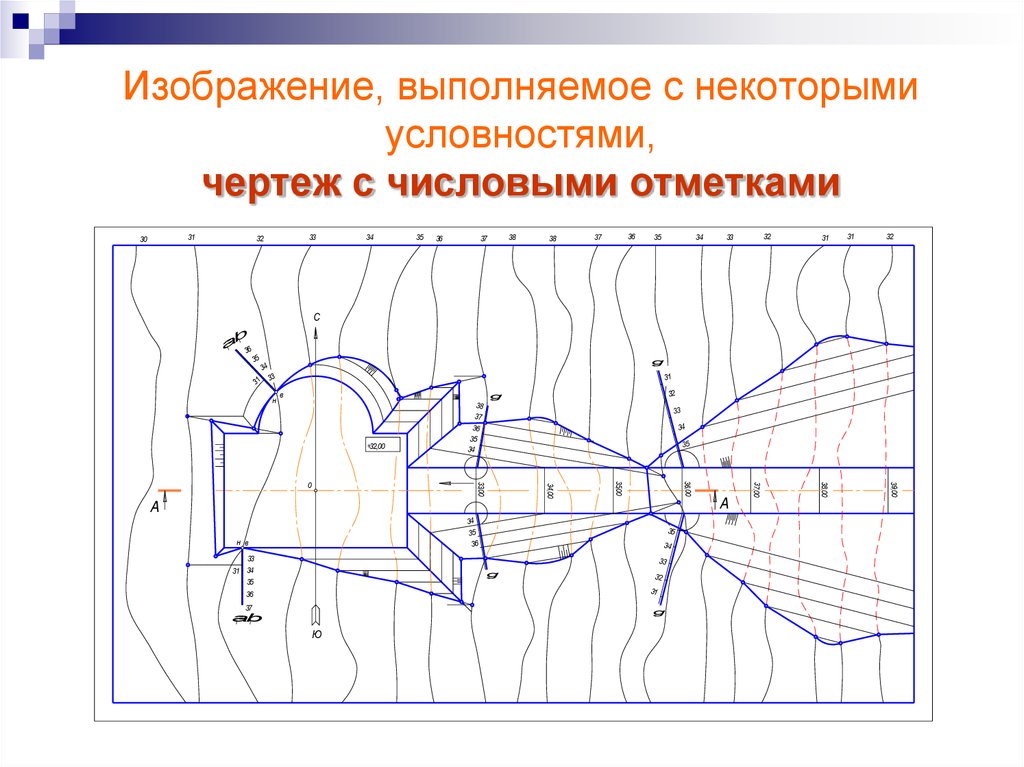
20. Изображение, выполняемое с некоторыми условностями, чертеж с числовыми отметками

31
30
33
32
34
35
36
38
37
38
36
37
35
34
32
33
31
31
32
С
35
g
i
34
31
i
=b
a
i
36
33
н
31
в
+32,00
33
34
35
31
36
37
g
i
a
i=b
i
Ю
iн =2:3
iв
32
39,00
33
g
i
38,00
33
31 34
35
35
34
А
37,00
34
35
36
н в
График масштабов уклонов
36,00
А
35,00
34,00
33,00
0
iв =1:1
32
g
i
38
37
36
35
34

21.

Чертеж является
международным графическим языком,
который должен быть понятен технически
грамотному человеку.
Начертательная геометрия грамматика этого языка.

22.

Для построения изображений
геометрических фигур начертательная
геометрия применяет метод
проецирования.
Получающиеся при этом изображения
называются
проекционными чертежами.

23.

Параметры – независимые величины,
значения которых служат для
различения элементов некоторого
множества между собой.
В геометрических задачах параметры
выделяют единственную фигуру
или подмножество фигур
из множества фигур,
соответствующих одному и тому же
определению.

24. Пример: множество всех возможных треугольников

25.

Ограничения, накладываемые на параметры:
1. Линейная независимость параметров.
Например, углы треугольника - линейно зависимы, так как = 180
- (
+
)
2 . а
0 , в
0 , с
0 - область определения
3. а + в
с, в + с
а , а + с
в - область допустимых значений
с
в
в
а
а

26.

Множество всех точек на прямой –
однопараметрическое множество (R1)

27.

Множество всех точек на плоскости –
двупараметрическое множество (R2)

28.

29.

PM
Точка - R
O
o
l
M
B
Прямая - R
B
M
E
M
K
A
Плоскость - R
1
C
A
C
E
2
D

30.

Задание параметров положения фигуры
на плоскости (в пространстве R2)
xФ
Ф
yФ
oФ
xвн
в
макс. ППф = 3
yв
a
о

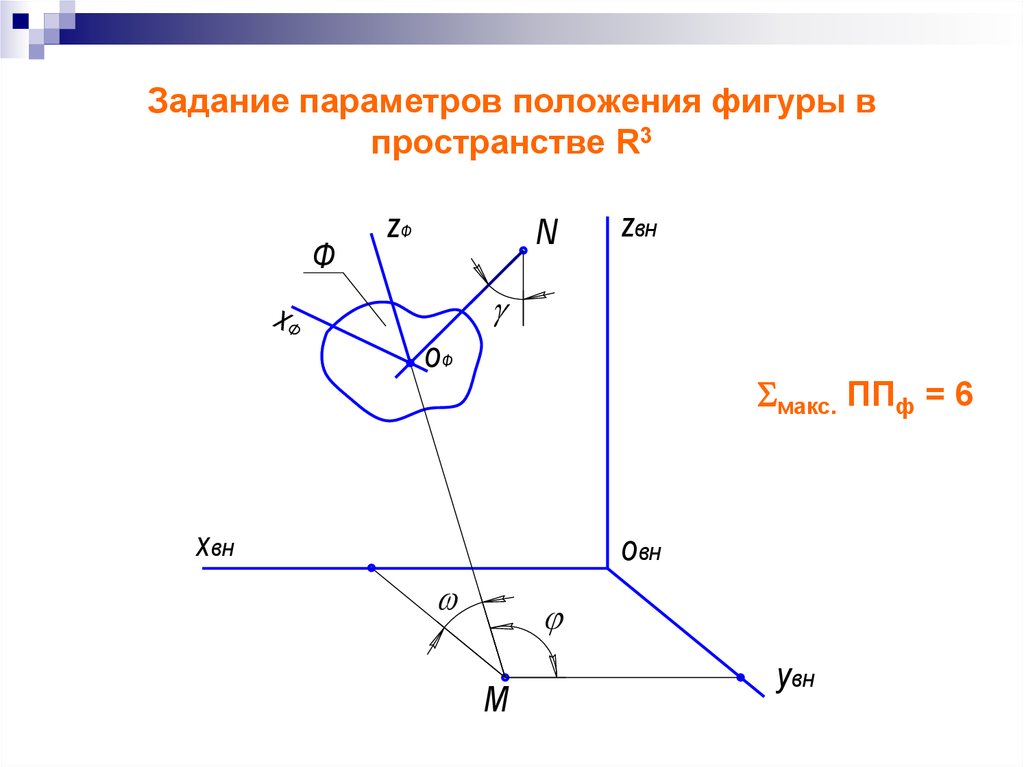
31. Задание параметров положения фигуры в пространстве R3

Ф
xФ
zФ
N
zвн
оФ
макс. ППф = 6
овн
xвн
M
yвн

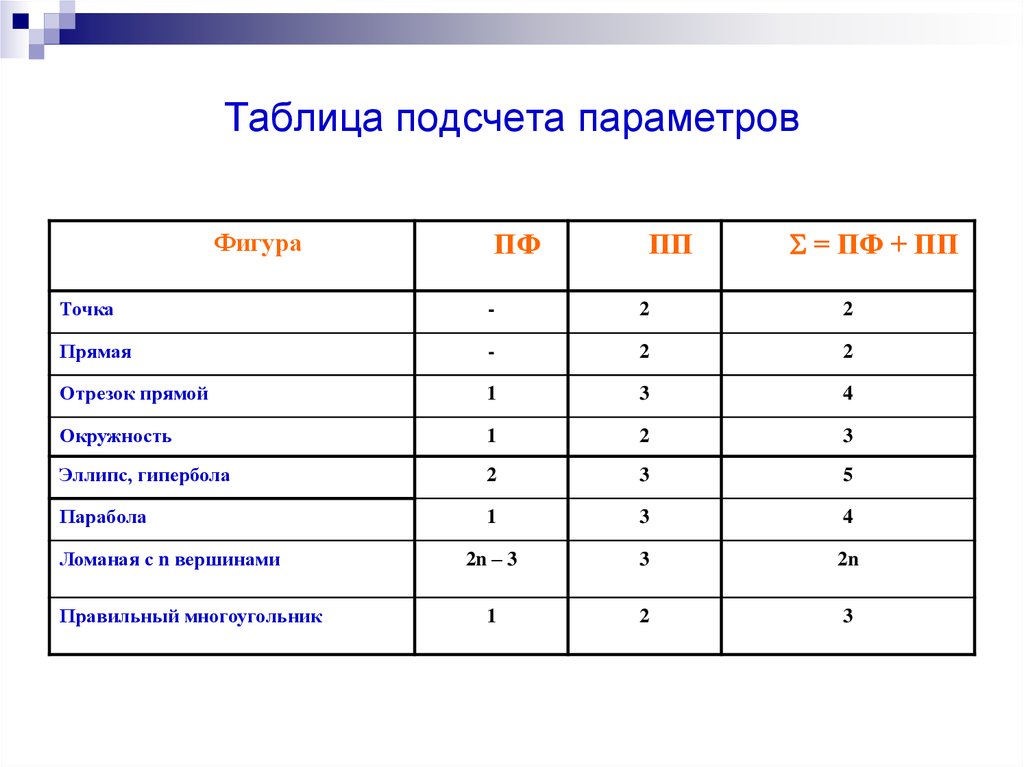
32. Таблица подсчета параметров

Фигура
ПФ
ПП
= ПФ + ПП
Точка
-
2
2
Прямая
-
2
2
Отрезок прямой
1
3
4
Окружность
1
2
3
Эллипс, гипербола
2
3
5
Парабола
1
3
4
2n – 3
3
2n
1
2
3
Ломаная с n вершинами
Правильный многоугольник

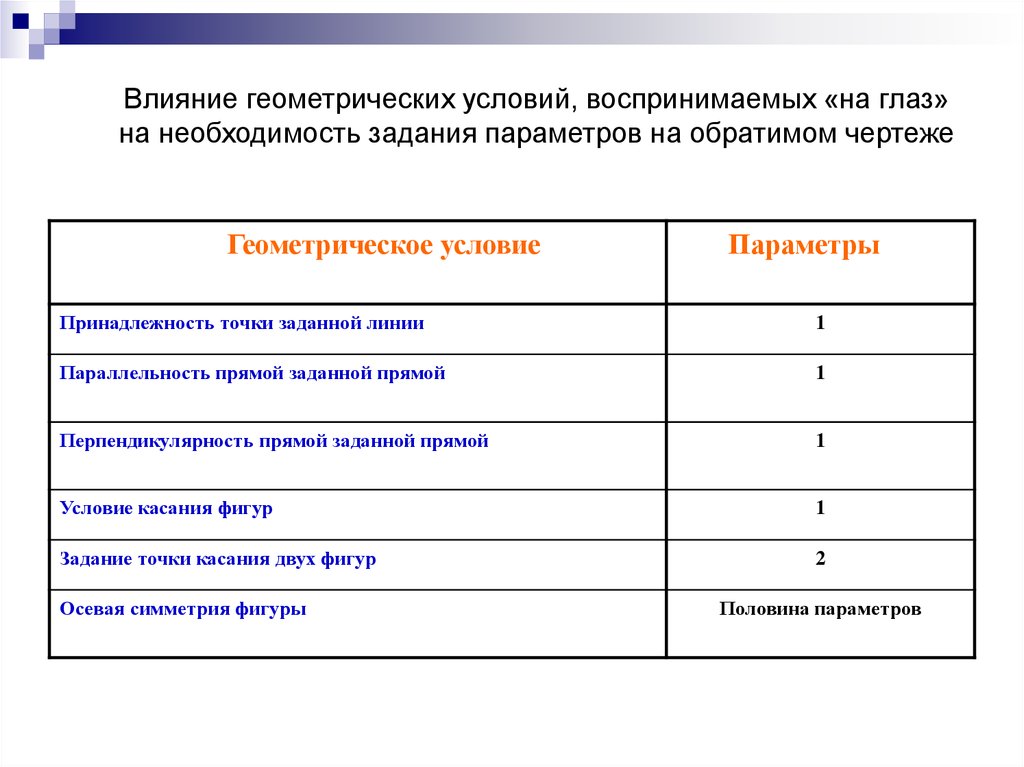
33.

Влияние геометрических условий, воспринимаемых «на глаз»
на необходимость задания параметров на обратимом чертеже
Геометрическое условие
Параметры
Принадлежность точки заданной линии
1
Параллельность прямой заданной прямой
1
Перпендикулярность прямой заданной прямой
1
Условие касания фигур
1
Задание точки касания двух фигур
2
Осевая симметрия фигуры
Половина параметров

34. Формула подсчета параметров фигуры:

ПФ = ПП + ПФ - ГУ

35. Пример параметризации фигуры

Таблица подсчета параметров
y
П8
П9
П6
О9
R
О10
О8
П7
О1
0
x
О3
О2
О5
П5
О6
П2
П1
R
О7
П4
О4
П3
О1
О2
О3
П1
О4
П2
О5
О6
П3
П4
О7
П5
П6
П8
О9
П7
П9
О10
О8
ПФ
ПП
1
1
1
0
1
0
1
1
0
0
1
0
0
0
1
0
0
1
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Геометрические условия:
ГУ
2
центр О1
т.0
центр О2
т.0
2
центр О3
т.0
2
1
П1 // 0Х
1
центр О4
0Y
П2 // 0Y, касается О4
2
ц.О5
0Y, кас. П2, сим.О4 отн. П1 3
1
центр О6
П1
касается О6 и О7
2
2
касается О6 и О4
1
центр О7
П1
2
касается О3, П5
(П1
0Y)
П6 // 0Х
1
1
П8 // 0Y
2
касается П6 и П8
2
касается О3, П7
(П6
О9)
П9 // 0Y, П9 сим. П8 отн-но 0Y
2
касается П6 иП9, симм.О9 отн.0Y 3
касается О7, О8
(П6
О10)
2
S
П
1
1
1
1
2
0
0
2
0
0
2
0
1
1
1
0
0
0
1
Итого: 14
Выполнил: студент группы N, Катков А.А.