Similar presentations:
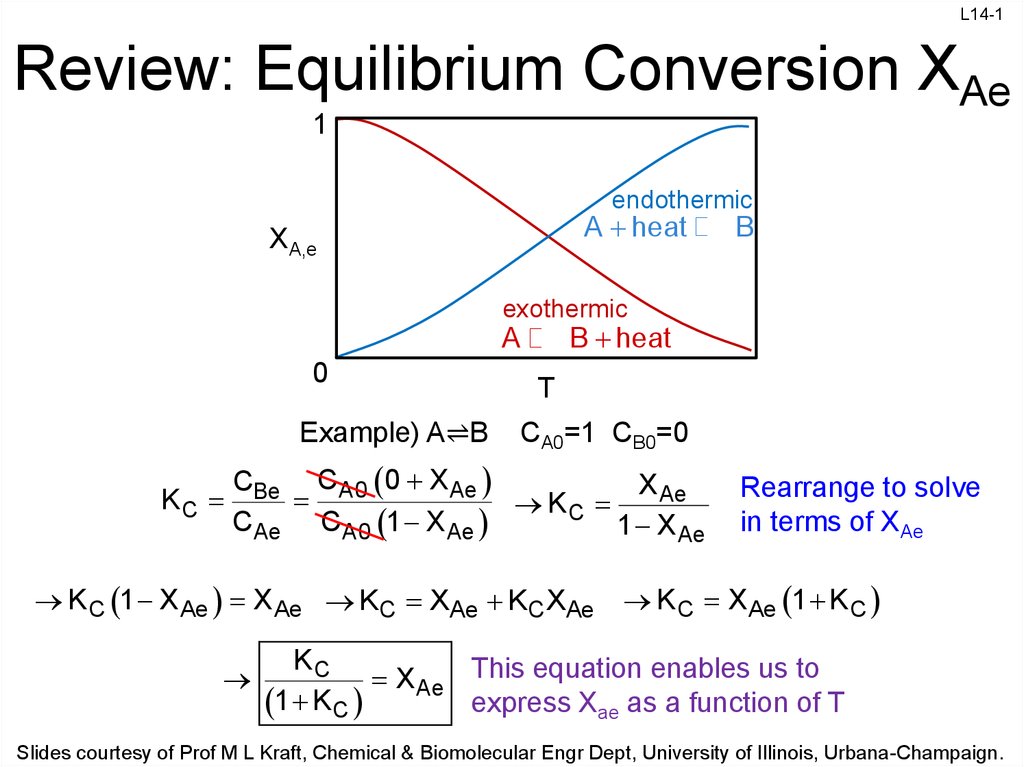
Review: Equilibrium Conversion XAe
1. Review: Equilibrium Conversion XAe
L14-1Review: Equilibrium Conversion XAe
1
endothermic
A heat
XA,e
B
exothermic
B heat
A
0
Example) A⇌B
KC
T
CA0=1 CB0=0
CBe CA0 0 X Ae
X Ae
KC
CAe CA0 1 X Ae
1 X Ae
K C 1 X Ae X Ae KC XAe KC XAe
Rearrange to solve
in terms of XAe
K C X Ae 1 K C
KC
X Ae This equation enables us to
express Xae as a function of T
1 K C
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
2. Review: XAe and Temperature
L14-2Review: XAe and Temperature
X Ae
Clicker question
material
1
H RX TR 1 1
1
exp
1
K C T2
R
T T2
H RX TR 1 1
Exothermic & CP =0: H RX TR 0, when T exp
T T & X Ae
R
2
Makes sense from Le Chatelier’s principle A
B heat
Exothermic rxn produces heat→
increasing temp adds heat (product) & pushes rxn to left (lower conversion)
H RX TR 1 1
Endothermic & Cp 0: H RX TR 0, when T exp
& X Ae
R
T T2
Makes sense from Le Chatelier’s principle A heat
B
Heat is a reactant in an endothermic rxn→
increasing temp adds reactant (heat) & pushes rxn to right (higher conversion)
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
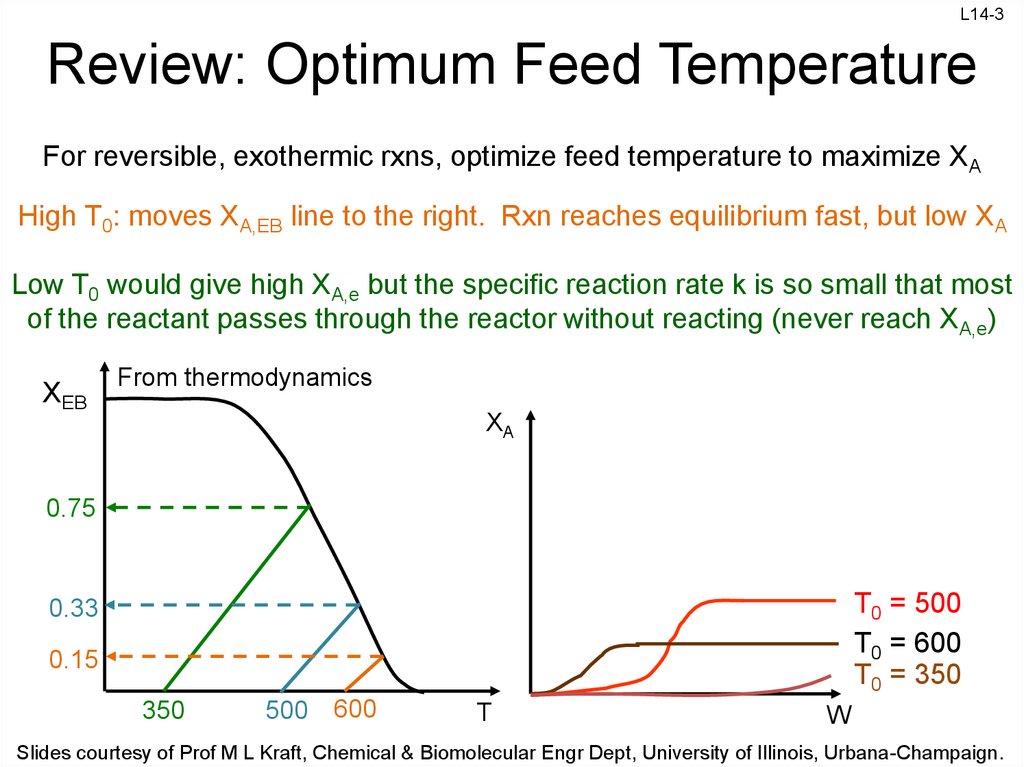
3. Review: Optimum Feed Temperature
L14-3Review: Optimum Feed Temperature
For reversible, exothermic rxns, optimize feed temperature to maximize XA
High T0: moves XA,EB line to the right. Rxn reaches equilibrium fast, but low XA
Low T0 would give high XA,e but the specific reaction rate k is so small that most
of the reactant passes through the reactor without reacting (never reach XA,e)
XEB
From thermodynamics
XA
0.75
T0 = 500
T0 = 600
T0 = 350
0.33
0.15
350
500
600
T
W
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
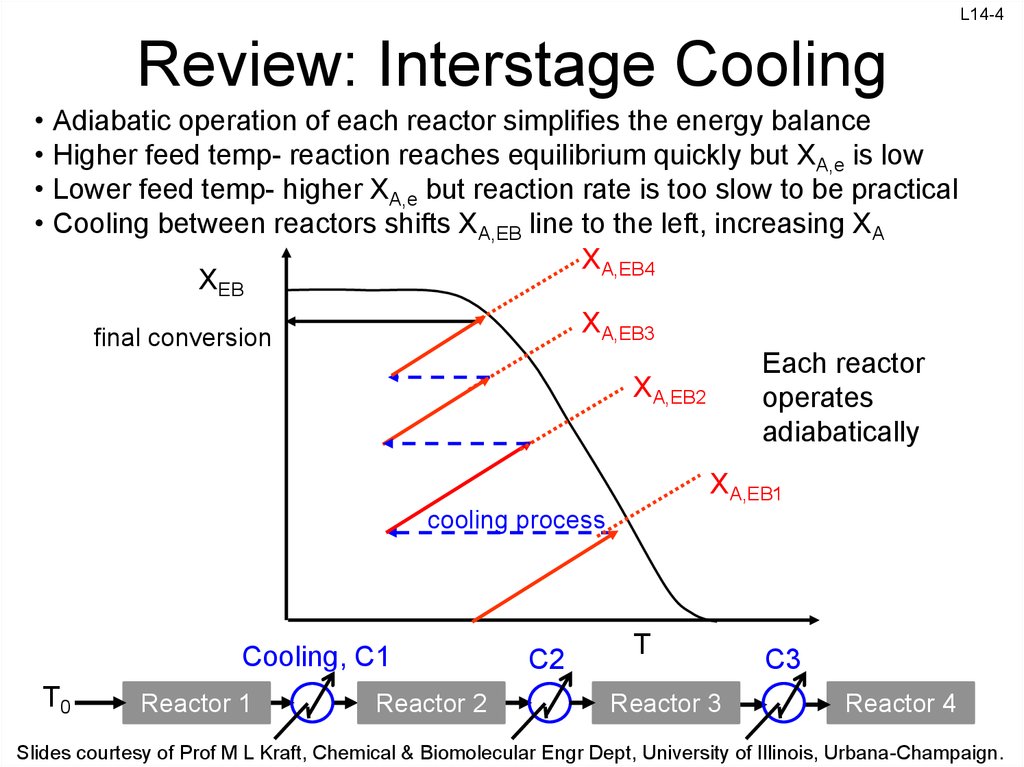
4. Review: Interstage Cooling
L14-4Review: Interstage Cooling
Adiabatic operation of each reactor simplifies the energy balance
Higher feed temp- reaction reaches equilibrium quickly but XA,e is low
Lower feed temp- higher XA,e but reaction rate is too slow to be practical
Cooling between reactors shifts XA,EB line to the left, increasing XA
XA,EB4
XEB
XA,EB3
final conversion
Each reactor
operates
adiabatically
XA,EB2
XA,EB1
cooling process
Cooling, C1
T0
Reactor 1
Reactor 2
C2
T
Reactor 3
C3
Reactor 4
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
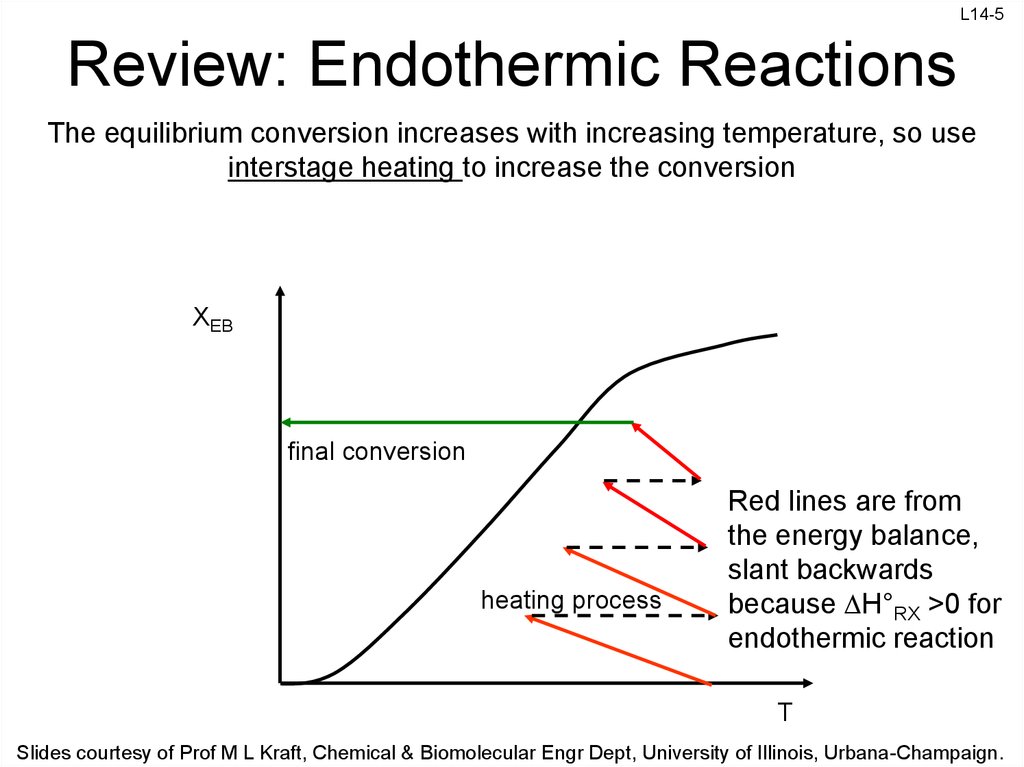
5. Review: Endothermic Reactions
L14-5Review: Endothermic Reactions
The equilibrium conversion increases with increasing temperature, so use
interstage heating to increase the conversion
XEB
final conversion
heating process
Red lines are from
the energy balance,
slant backwards
because H°RX >0 for
endothermic reaction
T
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
6. L14: Nonadiabatic PFR/PBR Operation and Reactor Stability
L14-6L14: Nonadiabatic PFR/PBR
Operation and Reactor Stability
1. T changes with distance down reactor- differential form of EB must be
used
2. Multiple steady states: more than one set of conditions satisfies both the
energy balance & mole balance
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
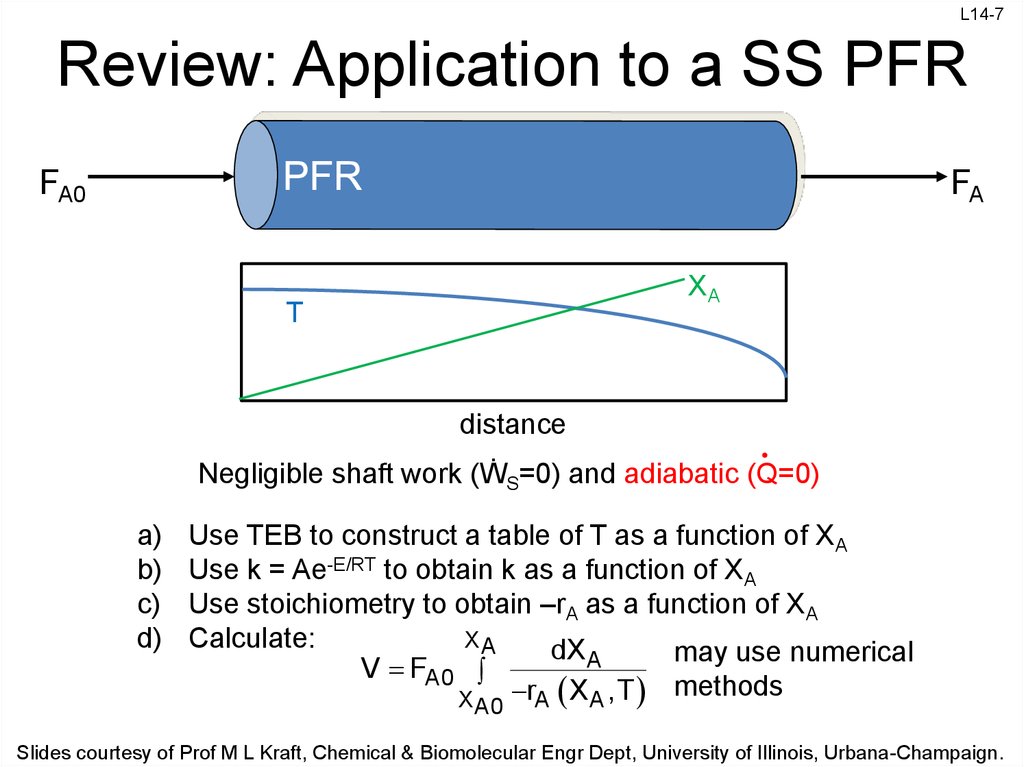
7. Review: Application to a SS PFR
L14-7Review: Application to a SS PFR
FA0
FA
XA
T
distance
Negligible shaft work (ẆS=0) and adiabatic (Q=0)
a)
b)
c)
d)
Use TEB to construct a table of T as a function of XA
Use k = Ae-E/RT to obtain k as a function of XA
Use stoichiometry to obtain –rA as a function of XA
XA
Calculate:
dX A
may use numerical
V FA0
rA X A ,T methods
X
A0
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
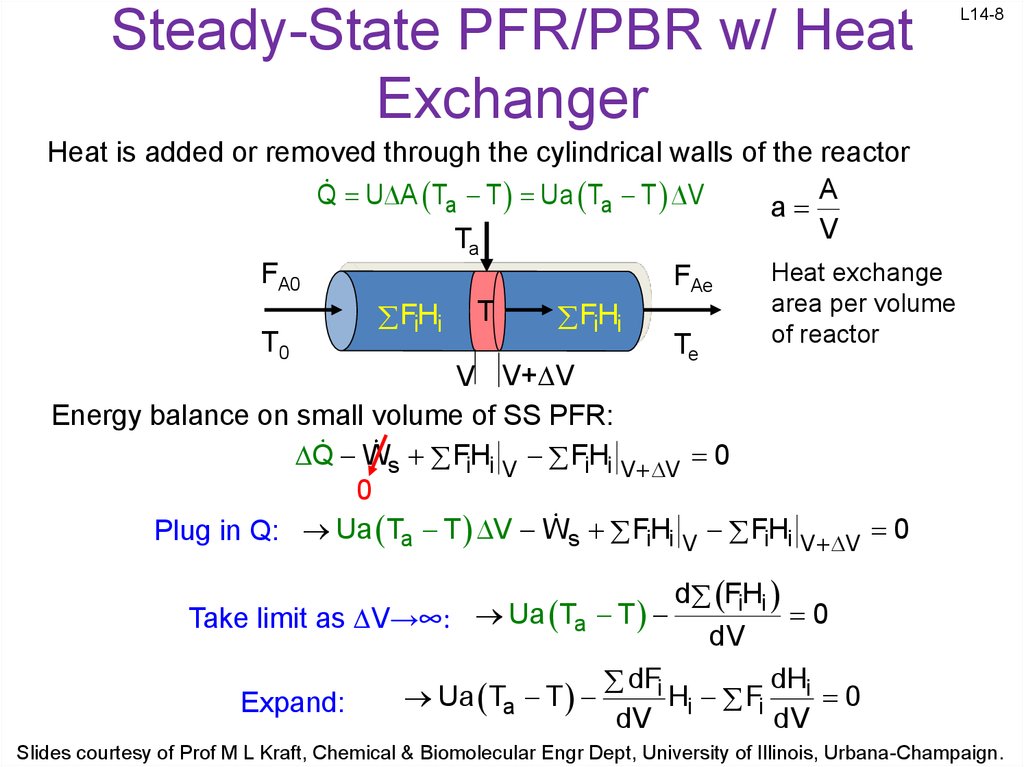
8. Steady-State PFR/PBR w/ Heat Exchanger
L14-8Heat is added or removed through the cylindrical walls of the reactor
A
Q U A Ta T Ua Ta T V
a
V
T
a
FA0
T0
FAe
FH
i i
T
FH
i i
Te
Heat exchange
area per volume
of reactor
V V+ V
Energy balance on small volume of SS PFR:
Q Ws FH
i i V FH
i i V V 0
0
Plug in Q: Ua Ta T V Ws FH
i i V FH
i i V V 0
d FiHi
0
Take limit as V→∞: Ua Ta T
dV
dHi
dFi
Ua
T
T
H
F
0
a
Expand:
i i
dV
dV
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
9. TEB for PFR/PBR w/ Heat Exchanger
L14-9TEB for PFR/PBR w/ Heat Exchanger
Ta
FA0
T0
FH
i i
T
FH
i i
FAe
Te
V V+ V
dHi
dFi
Ua Ta T
H Fi
0
dV i
dV
Substitute the differentials:
dFi
dHi
dT
r i rA and
Cpi
dV i
dV
dV
dT
Ua Ta T Hi i rA FiCPi
0
dV
iHi HRX
dT
Ua Ta T HRX rA FC
0
i Pi
dV
Solve for dT/dV:
dT HRX rA Ua Ta T
dT
FC
HRX rA Ua Ta T
i Pi
dV
dV
FC
i Pi
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
10. Energy Balance for Tubular Reactors
L14-10Energy Balance for Tubular Reactors
Heat
generated
Heat
removed
dT HRX rA Ua Ta T
dV
FiCPi
Substitute and multiply
out the denominator
dT H RX (TR ) CP T TR rA Ua Ta T C
i Pi
dV
FA0 iCPi CPi i X A
dT H RX (TR ) CP T TR rA Ua Ta T
dV
FA0 iCPi CP X A
dX A rA
dV
FA0
Heat
removed
Multiply Ua
and (Ta-T) by
dT HRX rA Ua T Ta
-1 (-1 x -1 = 1)
dV
FiCPi
HRX H RX (TR ) CP T TR
Fi FA0 i i X A
Heat
generated
Switched
sign & order
in bracket
for A B
b
CPB CPA CP
a
Energy balance for
SS PFR, Ẇs=0
PFR energy balance is coupled to the PFR design eq, and
PFR design eq is coupled to Arrhenius eq for k or Kequil
(these are the 3 equations that must be simultaneously solved)
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
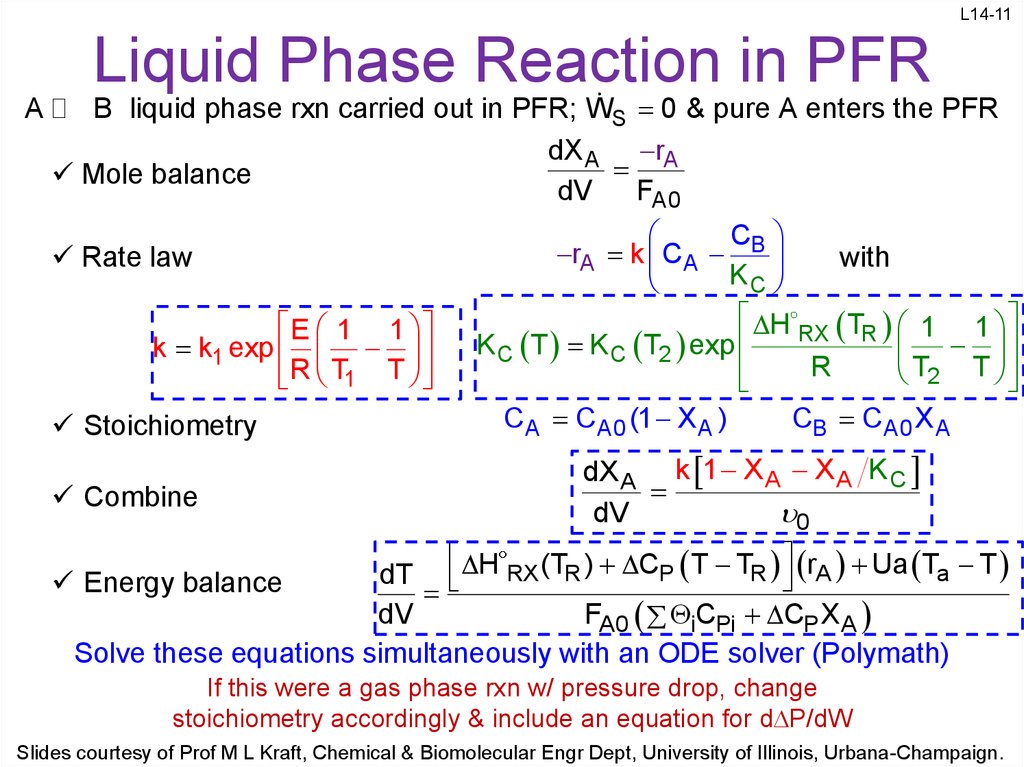
11. Liquid Phase Reaction in PFR
L14-11Liquid Phase Reaction in PFR
A
B liquid phase rxn carried out in PFR; WS 0 & pure A enters the PFR
dX A rA
Mole balance
dV
FA0
Rate law
E 1 1
k k1 exp
R T1 T
Stoichiometry
Combine
C
rA k C A B
with
KC
H RX TR 1 1
K C T K C T2 exp
R
T2 T
C A C A0 (1 X A )
CB C A0 X A
dX A k 1 X A X A K C
dV
0
H RX (TR ) CP T TR rA Ua Ta T
dT
Energy balance
dV
FA0 iCPi CP X A
Solve these equations simultaneously with an ODE solver (Polymath)
If this were a gas phase rxn w/ pressure drop, change
stoichiometry accordingly & include an equation for d P/dW
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
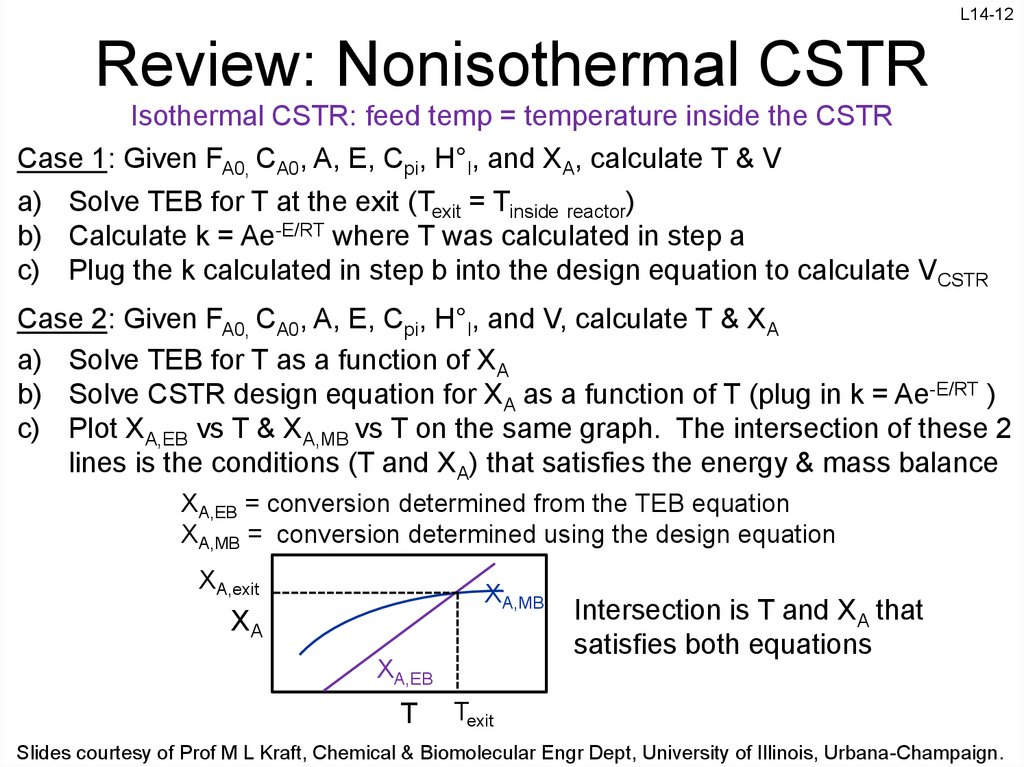
12. Review: Nonisothermal CSTR
L14-12Review: Nonisothermal CSTR
Isothermal CSTR: feed temp = temperature inside the CSTR
Case 1: Given FA0, CA0, A, E, Cpi, H°I, and XA, calculate T & V
a) Solve TEB for T at the exit (Texit = Tinside reactor)
b) Calculate k = Ae-E/RT where T was calculated in step a
c) Plug the k calculated in step b into the design equation to calculate VCSTR
Case 2: Given FA0, CA0, A, E, Cpi, H°I, and V, calculate T & XA
a) Solve TEB for T as a function of XA
b) Solve CSTR design equation for XA as a function of T (plug in k = Ae-E/RT )
c) Plot XA,EB vs T & XA,MB vs T on the same graph. The intersection of these 2
lines is the conditions (T and XA) that satisfies the energy & mass balance
XA,EB = conversion determined from the TEB equation
XA,MB = conversion determined using the design equation
XA,exit
XA,MB
XA
XA,EB
T
Intersection is T and XA that
satisfies both equations
Texit
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
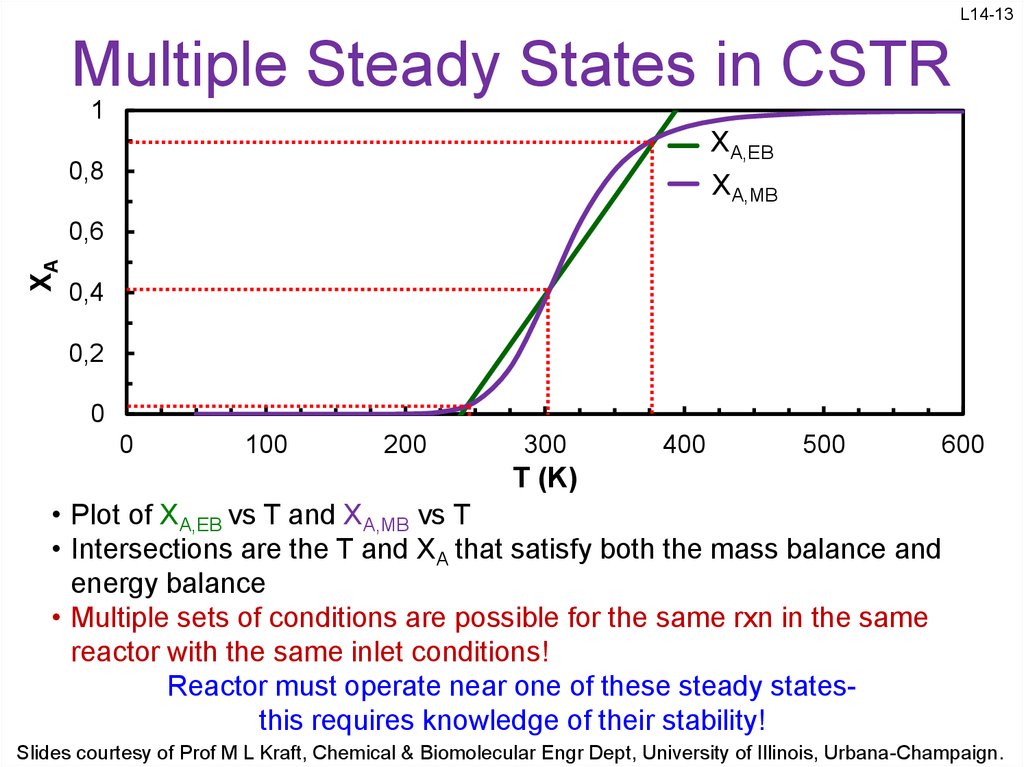
13. Multiple Steady States in CSTR
L14-13Multiple Steady States in CSTR
1
XA,EB
XA,MB
0,8
XA
0,6
0,4
0,2
0
0
100
200
300
400
500
600
T (K)
• Plot of XA,EB vs T and XA,MB vs T
• Intersections are the T and XA that satisfy both the mass balance and
energy balance
• Multiple sets of conditions are possible for the same rxn in the same
reactor with the same inlet conditions!
Reactor must operate near one of these steady statesthis requires knowledge of their stability!
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
14.
Consider a jacketed CSTR with constant heat capacity, negligible shaft L14-14work, CP=0, first order kinetics, all feeds at the same temperature (Ti0=T0),
constant Ta in jacket, and an overall heat transfer coefficient
Q UA Ta T
n
TEB : 0 Q FA0 iCp,i T Ti0 HRX (T)FA0 X A
i 1
Substituting for Q UA Ta T and HRX (T) HRX (TR ) since CP 0
n
0 UA Ta T FA0 iCp,i T Ti0 HRX (TR )FA0 XA
i 1
Bring terms that remove heat to other side of equation:
n
FA0 iCp,i T Ti0 UA Ta T HRX (TR )FA0 XA
i 1
n
iCp,i T Ti0
i 1
UA Ta T
HRX (TR )X A
FA0
Heat removed term ≡ R(T)
Heat generated term ≡ G(T)
A steady-state occurs when R(T) = G(T)
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
15. Even More Terms…
L14-15Even More Terms…
Heat removed term ≡ R(T)
n
iCp,i T Ti0
i 1
CP0 iCPi
Heat generated term ≡ G(T)
UA Ta T
HRX (TR )XA
FA 0
FA0 X A
rA V
V
XA
rA
FA 0
UA Ta T
rA V
HRX (TR )
Substitute Cp0 T Ti0
FA0
F
A0
More substitutions:
T0FA0Cp0 UATa Ta T0
UA
T
Cp0FA0 c
UA Cp0FA0
1
HRX HRX TR
Cp0 1 T TC HRX
Heat
removed: R T Cp0 1 T TC
rA V
F
A0
Heat
rA V
generated: G T HRX F
A0
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
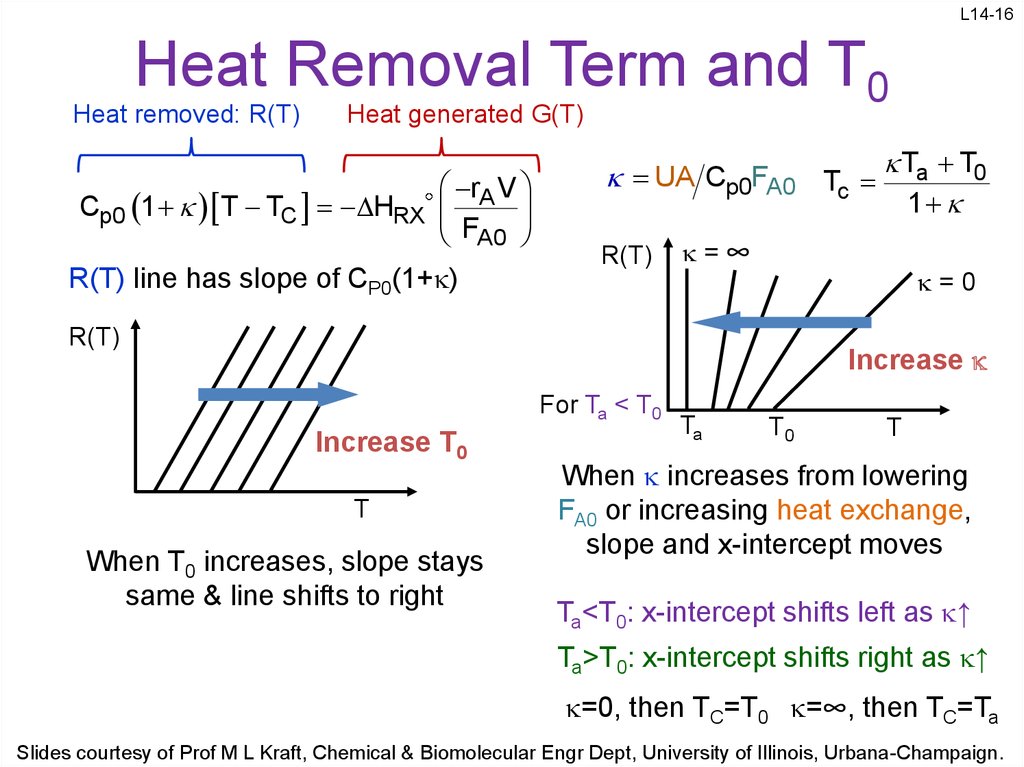
16. Heat Removal Term and T0
L14-16Heat Removal Term and T0
Heat removed: R(T)
Heat generated G(T)
Cp0 1 T TC HRX
rA V
F
A0
R(T) line has slope of CP0(1+ )
UA Cp0FA0 Tc Ta T0
1
R(T)
=∞
=0
R(T)
Increase
For Ta < T0
Increase T0
T
When T0 increases, slope stays
same & line shifts to right
Ta
T0
T
When increases from lowering
FA0 or increasing heat exchange,
slope and x-intercept moves
Ta<T0: x-intercept shifts left as ↑
Ta>T0: x-intercept shifts right as ↑
=0, then TC=T0 =∞, then TC=Ta
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
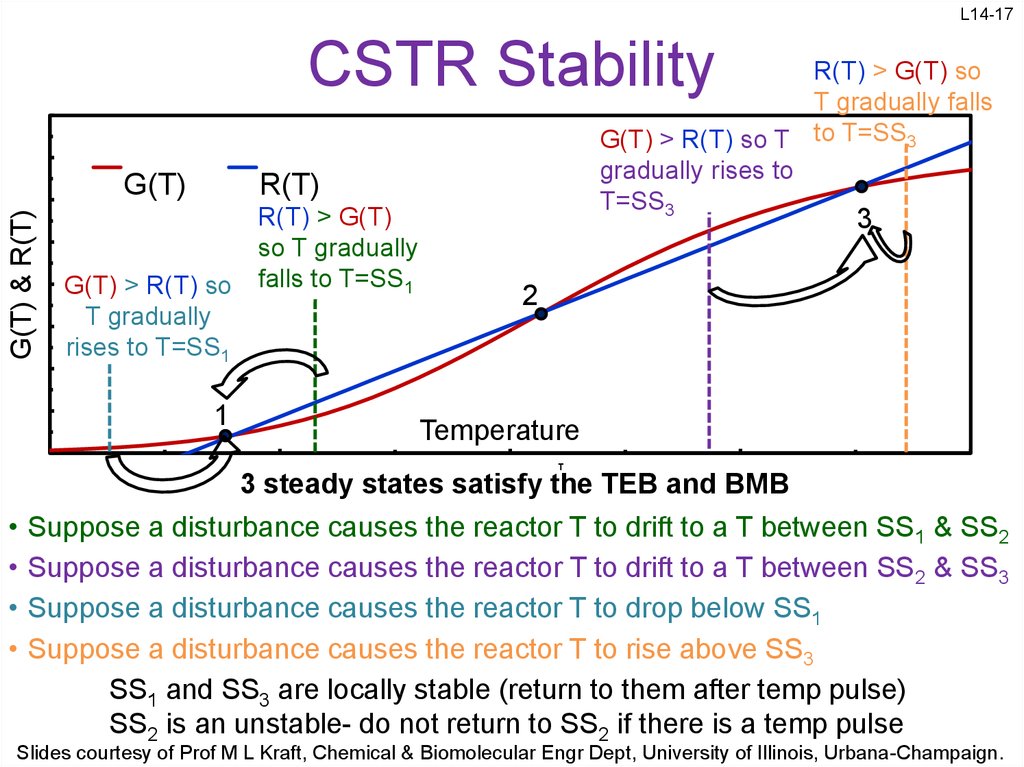
17. CSTR Stability
L14-17CSTR Stability
G(T) & R(T)
G(T)
R(T) > G(T) so
T gradually falls
G(T) > R(T) so T to T=SS3
gradually rises to
T=SS3
R(T)
G(T) > R(T) so
T gradually
rises to T=SS1
1
R(T) > G(T)
so T gradually
falls to T=SS1
3
2
Temperature
T
3 steady states satisfy the TEB and BMB
Suppose a disturbance causes the reactor T to drift to a T between SS1 & SS2
Suppose a disturbance causes the reactor T to drift to a T between SS2 & SS3
Suppose a disturbance causes the reactor T to drop below SS1
Suppose a disturbance causes the reactor T to rise above SS3
SS1 and SS3 are locally stable (return to them after temp pulse)
SS2 is an unstable- do not return to SS2 if there is a temp pulse
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
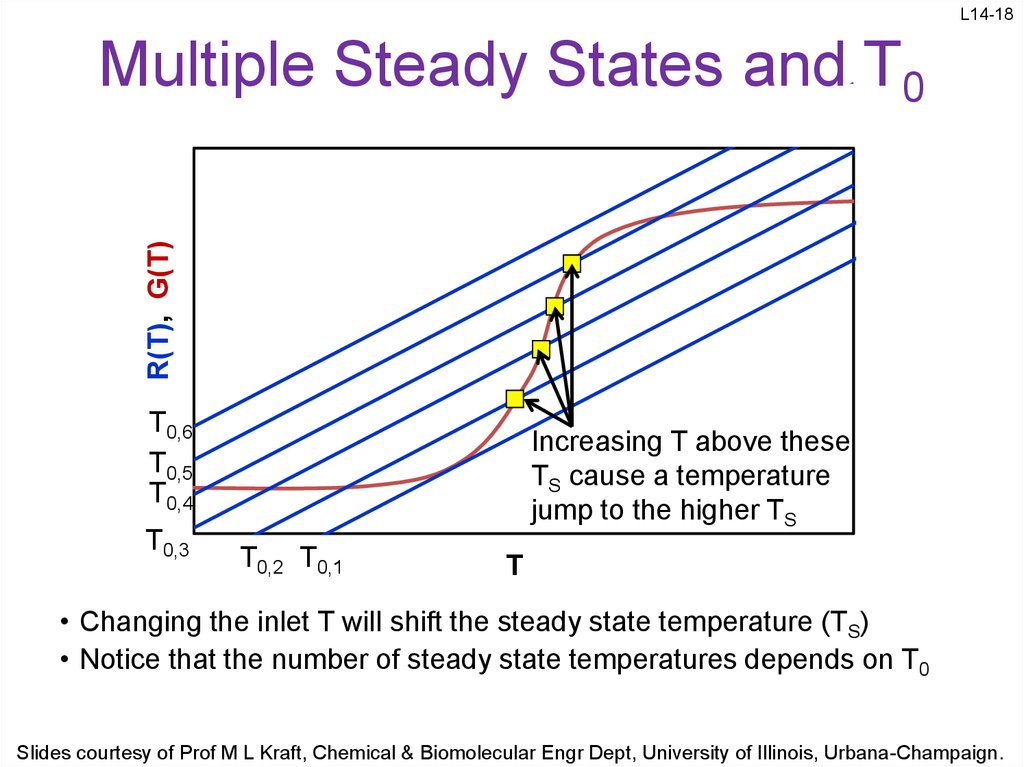
18. Multiple Steady States and T0
L14-18R(T), G(T)
Multiple Steady States and T0
T0,6
T0,5
T0,4
T0,3
Increasing T above these
TS cause a temperature
jump to the higher TS
T0,2 T0,1
T
TT
• Changing the inlet T will shift the steady state temperature (TS)
• Notice that the number of steady state temperatures depends on T0
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
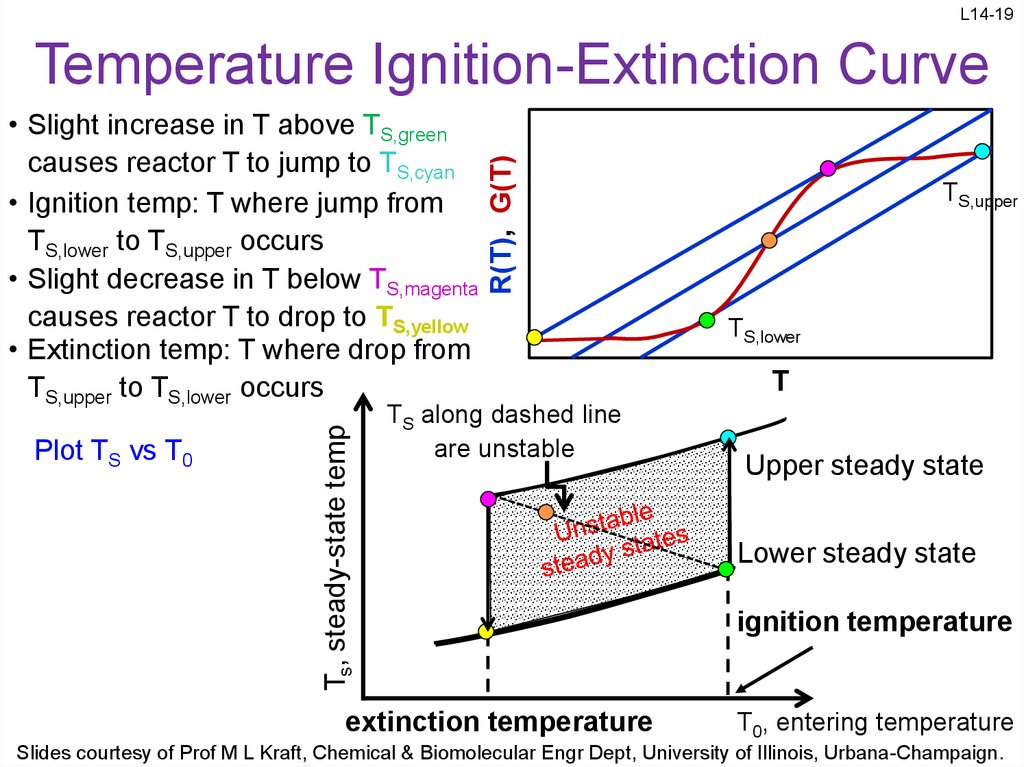
19. Temperature Ignition-Extinction Curve
L14-19Plot TS vs T0
Ts, steady-state temp
• Slight increase in T above TS,green
causes reactor T to jump to TS,cyan
• Ignition temp: T where jump from
TS,lower to TS,upper occurs
• Slight decrease in T below TS,magenta
causes reactor T to drop to TS,yellow
• Extinction temp: T where drop from
TS,upper to TS,lower occurs
R(T), G(T)
Temperature Ignition-Extinction Curve
TS along dashed line
are unstable
extinction temperature
TS,upper
TS,lower
T
Upper steady state
Lower steady state
ignition temperature
T0, entering temperature
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.
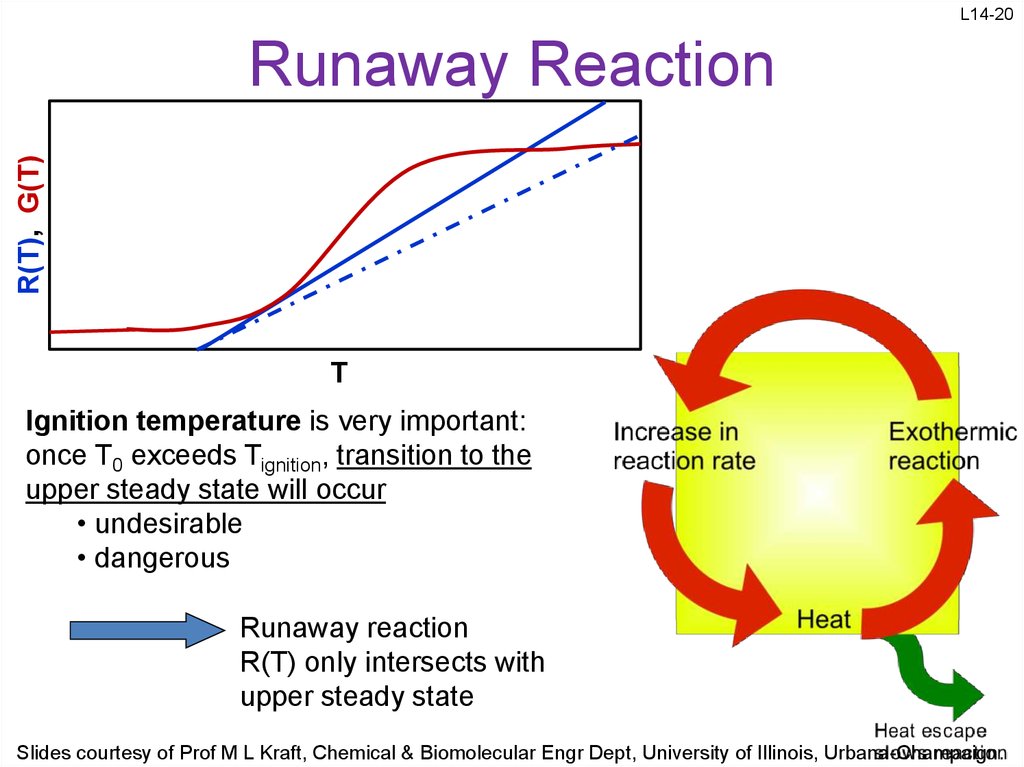
20. Runaway Reaction
L14-20R(T), G(T)
Runaway Reaction
T
Ignition temperature is very important:
once T0 exceeds Tignition, transition to the
upper steady state will occur
• undesirable
• dangerous
Runaway reaction
R(T) only intersects with
upper steady state
Slides courtesy of Prof M L Kraft, Chemical & Biomolecular Engr Dept, University of Illinois, Urbana-Champaign.






 physics
physics



