Similar presentations:
Решение неравенств
1.
Разработал Рыжих С.А.2.
Виды неравенств- Линейные
- Квадратные
+
_
+
3.
Виды неравенств- Рациональные
_
+
_
+
4.
Виды неравенств- Содержащие чётную степень
- Содержащие нечётную степень
5.
Виды неравенств- Иррациональные (корень чётной степени)
- Иррациональные (корень нечётной степени)
6.
Виды неравенств- Показательные
7.
Виды неравенств- Логарифмические
- Тригонометрические
Решаем неравенства, используя
тригонометрическую окружность, либо с
помощью графика соответствующей
функции
8.
Равносильность неравенств1.Перенос члена неравенства (с противоположным
знаком) из одной части неравенства в другую;
2. Умножение (деление) обеих частей неравенства
на положительное число;
3. Применение правил умножения многочленов и
формул сокращённого умножения;
4. Приведение подобных членов многочлена;
5. Возведение неравенства в нечётную степень;
6. Логарифмирование неравенства
т.е замена этого неравенства неравенством
9.
Равносильность неравенствна некотором множестве чисел
1.Возведение неравенства в чётную
степень;
2.Потенцирование неравенства;
3. Применение некоторых формул
(логарифмических,
тригонометрических и др.)
10.
Равносильны ли неравенства?И
И
И
И
11.
Методы решения неравенствалгебраический
графический
функциональны
й
геометрический
12.
Алгебраические методырешения неравенств
1) Сведение неравенства к
равносильной системе или
совокупности систем
2) Метод рационализации
3) Метод интервалов
13.
Сведение неравенства к равносильнойсовокупности систем неравенств
14.
Решите неравенствоРешение
15.
16.
Метод рационализацииЕсли
Аналогично можно доказать , что если
17.
Ответ18.
Заменяемое выражениеИспользуемое выражение
Решите неравенство
19.
Решите неравенство20.
Решение.21.
22.
23.
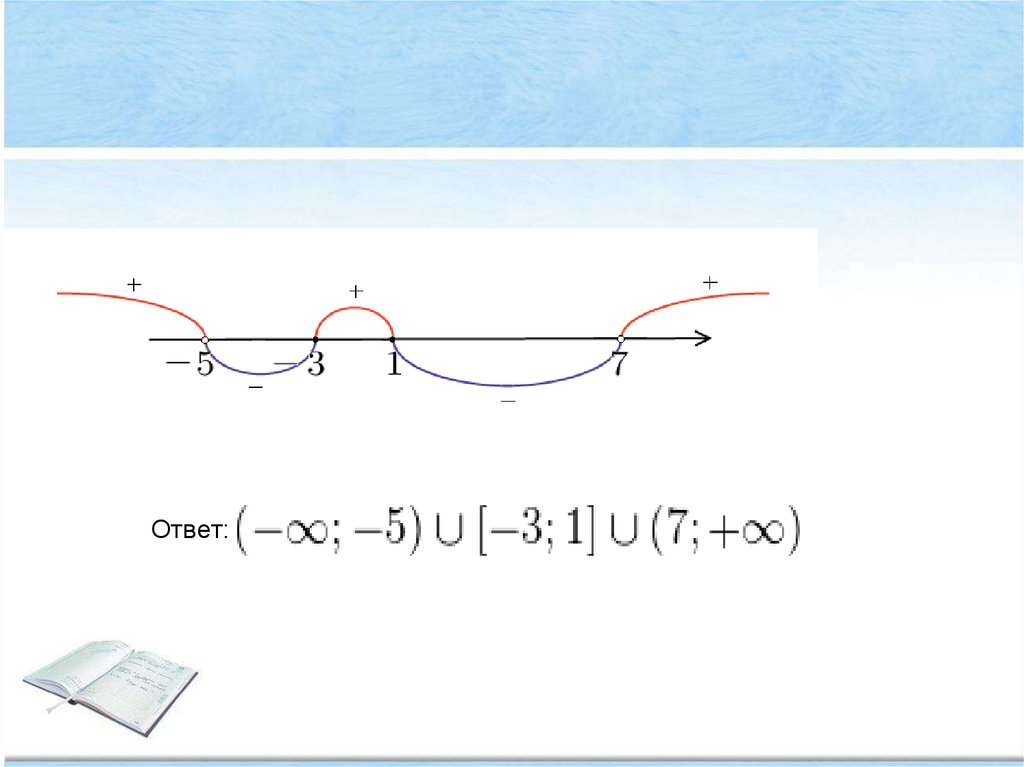
Метод интерваловАлгоритм решения:
1) Преобразовать неравенство так, чтобы в правой части
неравенства был ноль
2) Левую часть неравенства рассмотреть как функцию,
найти область определения и нули функции
3) Расположить нули функции в порядке возрастания на
числовой прямой, учитывая область определения
4) Определить знаки функции на каждом интервале
5) Рассматривая рисунок записать ответ
24.
Решим методом интервалов25.
Решениех1 и х2 - корни квадратного уравнение
26.
Рисуем ось Х и расставляем точки, в которых числитель изнаменатель обращаются в нуль


























 mathematics
mathematics








