Similar presentations:
Дисперсионный анализ
1. ДИСПЕРСИОННЫЙ АНАЛИЗ
2. Возможности дисперсионного анализа: 1. Оценка силы и достоверности влияний. 2. Оценка разности частных средних и частных долей.
3. Оценка наследуемости признаков вопределенных группах особей при передаче
генетической информации из поколения в
поколение.
4. Анализ комбинационной способности ♀ и
♂ линий.
3. Результативный признак – признак, изменяющийся под влиянием различных причин X, Y, Z. Факторы, вызывающие изменение признака,
Результативныйпризнак
–
признак,
изменяющийся под влиянием различных причин X, Y, Z.
Факторы, вызывающие
обозначаются А, В, С.
изменение
признака,
Организованные (регулируемые) факторы –
испытывают серийно, в виде нескольких независимых
друг от друга доз (градаций).
4. Типы дисперсионных комплексов: • Однофакторные; • Двух-, трех- и многофакторные; • Равномерные, пропорциональные –
ортогональные;• Неравномерные – неортогональные.
5. Dy=Dx+De, где Dx – межгрупповая дисперсия, представляющая собой сумму квадратов отклонений групповых средних от общей средней
комплекса, взвешенную начисленность вариант в группах n.
6. 1. Факториальная (межгрупповая) дисперсия равна сумме взвешенных квадратов центральных отклонений частных средних Мi по
градациямкомплекса от общей средней МΣ:
2
Сх = Σn (Mi - MΣ)
7. Случайная дисперсия (внутригрупповая) равна сумме квадратов центральных отклонений дат (V) от своих частных средних (Mi) по
градациям комплекса:Сz = Σ (V –
2
Mi)
8. Общая дисперсия равна сумме квадратов центральных отклонений дат (V) от общей средней: Сy = Σ (V - MΣ)2
Общая дисперсия равна сумме квадратовцентральных отклонений дат (V) от общей
средней:
Сy = Σ (V -
2
MΣ)
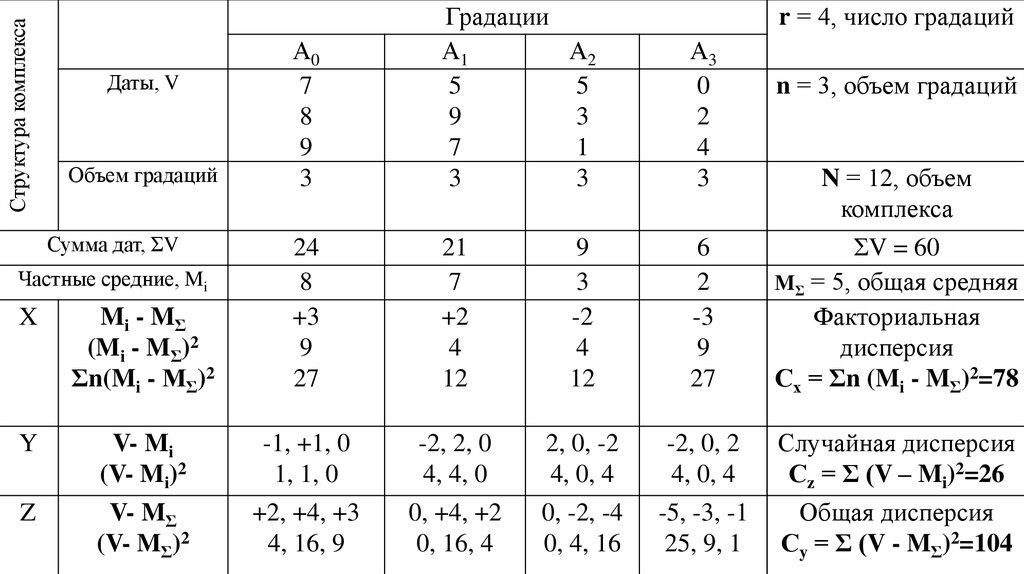
9.
Структура комплексаДаты, V
Объем градаций
Сумма дат, ΣV
А0
7
8
9
3
Градации
А1
А2
5
5
9
3
7
1
3
3
А3
0
2
4
3
21
7
+2
4
12
9
3
-2
4
12
6
2
-3
9
27
N = 12, объем
комплекса
ΣV = 60
MΣ = 5, общая средняя
Факториальная
дисперсия
Сх = Σn (Mi - MΣ)2=78
-2, 2, 0
4, 4, 0
0, +4, +2
0, 16, 4
2, 0, -2
4, 0, 4
0, -2, -4
0, 4, 16
-2, 0, 2
4, 0, 4
-5, -3, -1
25, 9, 1
Случайная дисперсия
Сz = Σ (V – Mi)2=26
Общая дисперсия
Сy = Σ (V - MΣ)2=104
X
M i - MΣ
(Mi - MΣ)2
Σn(Mi - МΣ)2
24
8
+3
9
27
Y
V- Mi
(V- Mi)2
V- MΣ
(V- MΣ)2
-1, +1, 0
1, 1, 0
+2, +4, +3
4, 16, 9
Частные средние, Mi
Z
r = 4, число градаций
n = 3, объем градаций
10. Закон аддитивности: в любом дисперсионном комплексе сумма частных дисперсий (факториальной и случайной) равна общей: Сх+ Сz= Сy
(78+26)=10411. Основной показатель силы влияния
Сх 780, 75
С y 104
2
х
12. Эмпирический критерий достоверности силы влияния
Сх N r 78 8F
8, 0 Fst
С y r 1 26 3
13. Ошибка репрезентативности
r 1m 2 (1 )
х
N r
2
х
14. Фактически полученное дисперсионное отношение является величиной случайной, его необходимо сравнить с табличным (стандартным)
Фактически полученное дисперсионное отношение являетсявеличиной случайной, его необходимо сравнить с табличным
(стандартным) значением критерия Фишера Fst для принятого
уровня значимости а и чисел степеней свободы. При этом число
степеней свободы для большей дисперсии находят в верхней
строке, а для меньшей - в первом столбце таблицы Фишера.
15. На учебно-опытном участке агростанции изучали влияние различных способов внесения в почву органических удобрений на урожай
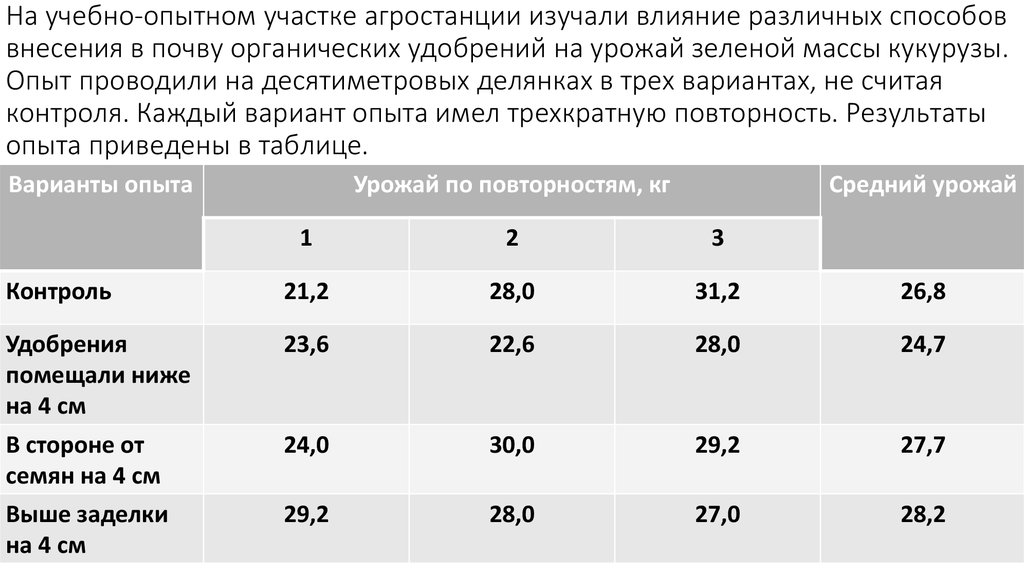
На учебно-опытном участке агростанции изучали влияние различных способоввнесения в почву органических удобрений на урожай зеленой массы кукурузы.
Опыт проводили на десятиметровых делянках в трех вариантах, не считая
контроля. Каждый вариант опыта имел трехкратную повторность. Результаты
опыта приведены в таблице.
Варианты опыта
Урожай по повторностям, кг
Средний урожай
1
2
3
Контроль
21,2
28,0
31,2
26,8
Удобрения
помещали ниже
на 4 см
23,6
22,6
28,0
24,7
В стороне от
семян на 4 см
Выше заделки
на 4 см
24,0
30,0
29,2
27,7
29,2
28,0
27,0
28,2






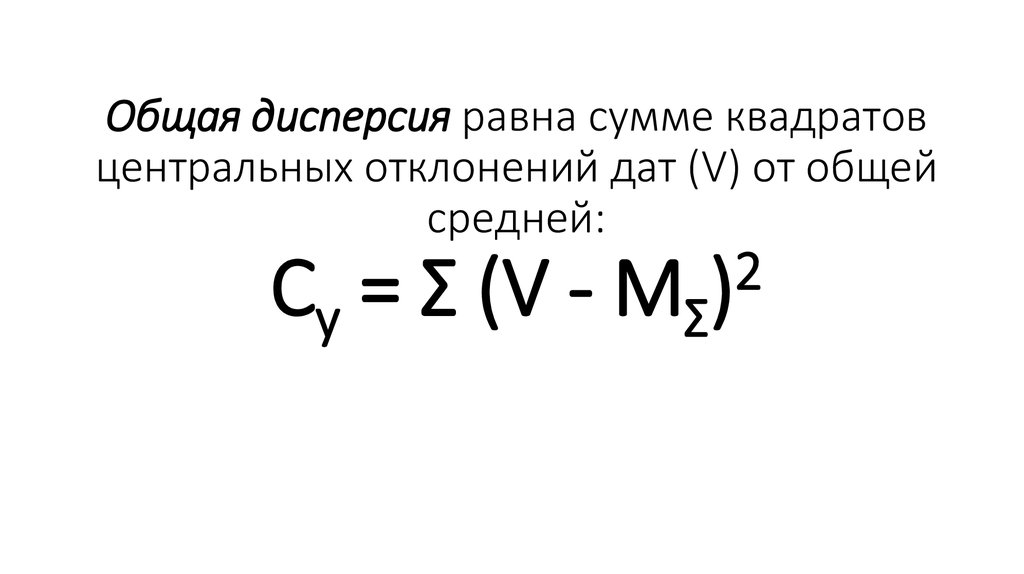



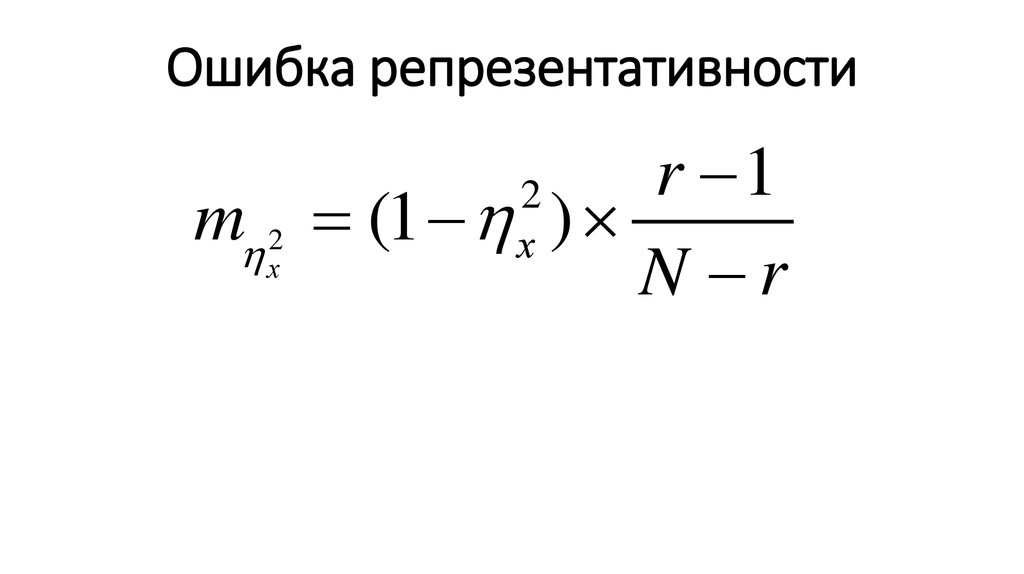

 biology
biology








