Эконометрика-II. Причинность по Грейнджеру для N временных рядов

1. Эконометрика-II

Лекция 3
28.02.2018

2. Причинность по Грейнджеру для N временных рядов

y1 , y2 , … , yN – N
yt y1t , , y N , t
T
временных рядов,
– векторный временной ряд, образованный
этими N рядами
Рассматриваем разбиение
где
yt на две части:
y t 1
y t 2
yt
yt 1 y1t , , y N1 , t
T ,
yt 2 y N1 1 , t , , y N , t
T ,
1 N1 N

3.

yt c1 11 L 12 L 13 L yt 1t
z t c2 21 L 22 L 23 L z t 2t
x c L L L x
t 3 31
23
33
t 3t
G
Непосредственный перенос условия G-причинности x
для VAR с двумя переменными на VAR с тремя переменными
приводит к следующему условию отсутствия такой связи:
y
13 L 0
Но если остальные элементы матрицы отличны от нуля, то тогда
G
G
x z и z y
т.е. такое определение Gпричинности не является транзитивным в системах с тремя и
более переменными.
Это определение не учитывает возможность опосредованного
влияния переменной x на переменную y через “промежуточную”
переменную
z.

4. Блочная экзогенность (block exogeneity)

Блочная экзогенность одной группы переменных (или
некоторой переменной) в отношении другой группы
переменных (или другой переменной) :
запаздывающие значения переменных второй группы не
входят в уравнения для переменных первой группы.

5.

y t c 1 y t 1 p y t p t ,
t ~ i .i .d . N 0 ,
y t 1
y t 2
yt
y it
i 1Ti y t 1 1 T1i y t 21 2Ti y t 1 2 T2 i y t 2 2 Tpi yt 1 p Tpi y t 2 p uit
H 0 : 1i 2i pi 0 , i 1, 2 , , N1
– Гипотеза блочной экзогенности первой группы
переменных в отношении второй группы переменных
Если эта гипотеза выполняется, то в порождении переменных первой группы
не участвуют переменные второй группы.
N2 уравнений второй группы образуют открытую VAR

6. Проверка гипотезы блочной экзогенности

Рассмотренная выше гипотеза блочной экзогенности первой
группы переменных в отношении второй группы переменных
накладывает N1N2 p ограничений на коэффициенты VAR(p) для
N переменных, и при N1 >1 имеет перекрестный характер,
затрагивая коэффициенты сразу нескольких уравнений
(точнее, коэффициенты N1 уравнений).
Проверить эту гипотезу можно, применяя критерий
отношения правдоподобий , статистика которого равна
LR 2 lUNRESTR l RESTR , где lUNRESTR – логарифм
максимума функции правдоподобия при оценивании VAR(p) без
ограничений на коэффициенты, а lRESTR – логарифм максимума
функции правдоподобия при оценивании VAR(p) с ограничениями
на коэффициенты, соответствующими проверяемой гипотезе.

7. Проверка гипотезы блочной экзогенности

ˆ RESTR ln
ˆ UNRESTR
LR 2 lUNRESTR l RESTR T ln
ˆ
– определитель оцененной ковариационной матрицы
инноваций, вычисляемой двумя разными способами:
1
1
T или ˆ
T
ˆ
det ˆ t ˆ t
det
ˆ t ˆ t
T t
T p t
Если VAR стабильна, то статистика LR имеет
асимптотическое распределение хи-квадрат с числом
степеней свободы, равным количеству зануляемых
коэффициентов

8.

Причинность по Грейнджеру в модели VAR с тремя переменными
Yt = 0.6 Yt – 1 + 0.5 Zt – 1 + ε1t ,
Xt = 0.6 Xt – 1 + 0.25 Zt – 1 + ε2t ,
Zt = 0.25 Xt – 1 + 0.6 Zt – 1 + ε3t .
Является ли переменная X
G-причиной для переменной Y ?
Zt – 1 = 0.25 Xt – 2 + 0.6 Zt – 2 + ε3, t –1
Yt = 0.6 Yt – 1 + 0.125 Xt – 2 + 0.3 Zt – 2 + ε1t + 0.5 ε3, t –1.
Группа 1: переменная Y
Группа 2: переменные X и Z
Переменные группы 2 являются G-причиной для Y

9.

Yt = 0.6 Yt – 1 + 0.5 Zt – 1 + ε1t ,
Xt = 0.6 Xt – 1 + 0.25 Zt – 1 + ε2t ,
Zt = 0.25 Xt – 1 + 0.6 Zt – 1 + ε3t .
Yt = 0.6 Yt – 1 + 0.125 Xt – 2 + 0.3 Zt – 2 + ε1t + 0.5 ε3, t –1
Xt – 1 не входит в последнее уравнение
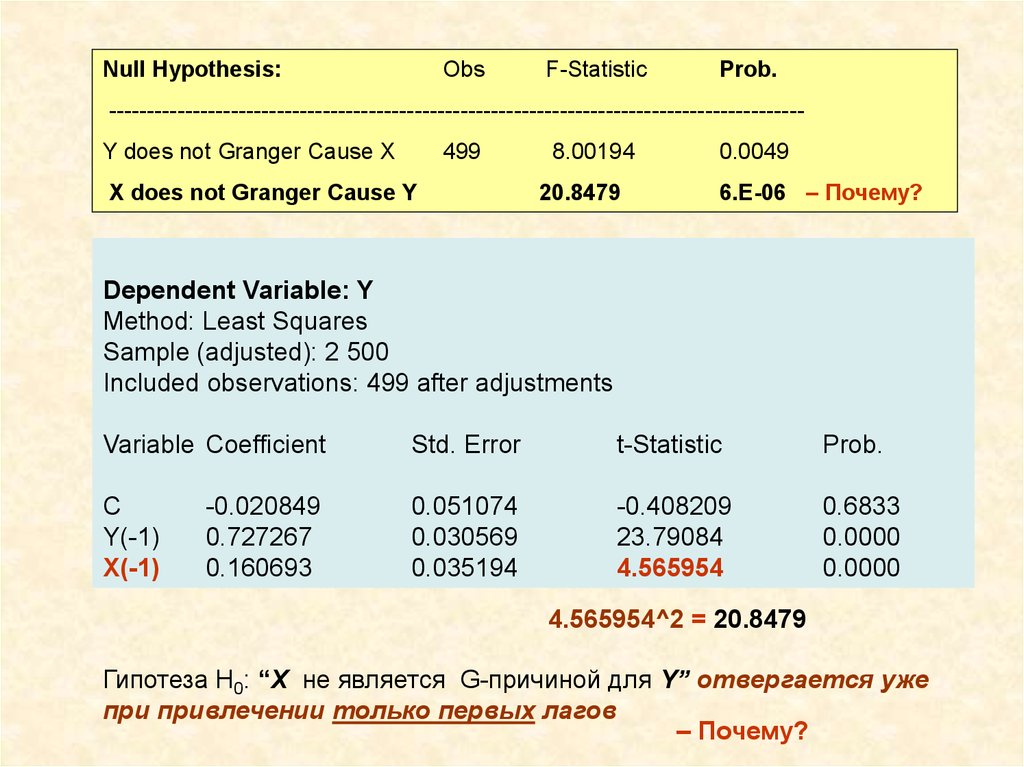
Pairwise Granger Causality Tests
Sample: 1 500
Lags: 1
Null Hypothesis:
Obs
F-Statistic
Prob.
-------------------------------------------------------------------------------------------
Y does not Granger Cause X
499
X does not Granger Cause Y
8.00194
0.0049
20.8479
6.E-06 – Почему?
------------------------------------------------------------------------------------------Z does not Granger Cause X
499
X does not Granger Cause Z
48.1778
1.E-11
28.6382
1.E-07
-------------------------------------------------------------------------------------------Z does not Granger Cause Y
Y does not Granger Cause Z
499
187.416
2.E-36
0.07788
0.7803

10.

Null Hypothesis:
Obs
F-Statistic
Prob.
------------------------------------------------------------------------------------------Y does not Granger Cause X
499
X does not Granger Cause Y
8.00194
20.8479
0.0049
6.E-06 – Почему?
Dependent Variable: Y
Method: Least Squares
Sample (adjusted): 2 500
Included observations: 499 after adjustments
Variable Coefficient
Std. Error
t-Statistic
Prob.
C
Y(-1)
X(-1)
0.051074
0.030569
0.035194
-0.408209
23.79084
4.565954
0.6833
0.0000
0.0000
-0.020849
0.727267
0.160693
4.565954^2 = 20.8479
Гипотеза H0: “X не является G-причиной для Y” отвергается уже
при привлечении только первых лагов
– Почему?

11.

Yt = 0.6 Yt – 1 + 0.5 Zt – 1 + ε1t ,
Xt = 0.6 Xt – 1 + 0.25 Zt – 1 + ε2t ,
Zt = 0.25 Xt – 1 + 0.6 Zt – 1 + ε3t .
Zt – 1 = 4 (Xt – 0.6 Xt – 1 – ε2t )

12.

Yt = 0.6 Yt – 1 + 0.5 Zt – 1 + ε1t ,
Xt = 0.6 Xt – 1 + 0.25 Zt – 1 + ε2t ,
Zt = 0.25 Xt – 1 + 0.6 Zt – 1 + ε3t .
Vector Autoregression Estimates
Sample (adjusted): 2 500
Included observations: 499 after adjustments
Standard errors in ( ) & t-statistics in [ ]
X
X(-1)
Y(-1)
Z(-1)
Y
Z
0.628552
0.009516
0.193404
(0.03449)
(0.03226)
(0.03331)
[ 18.2258]
[ 0.29503]
[ 5.80632]
0.012857
0.595029
-0.038285
(0.03057)
(0.02860)
(0.02953)
[ 0.42054]
[ 20.8081]
[-1.29648]
0.241654
0.435552
0.686442
(0.03696)
(0.03456)
(0.03569)
[ 6.53908]
[ 12.6011]
[ 19.2317]

13.

Из VAR:
Proc/ Make System
X = C(1)*X(-1) + C(2)*Y(-1) + C(3)*Z(-1)
Y = C(4)*X(-1) + C(5)*Y(-1) + C(6)*Z(-1)
Z = C(7)*X(-1) + C(8)*Y(-1) + C(9)*Z(-1)
Estimate/ Ordinary Least Squares
c(4)=c(7)=0
Wald Test:
System: Untitled
Test Statistic
Chi-square
Value
33.80044
df
2
Probability
0.0000
c(4)=c(6)=0
Wald Test:
System: Untitled
Test Statistic
Chi-square
Value
188.9828
df
2
Probability
0.0000

14.

Группа 1: переменная Y
Группа 2: переменные X и Z
Из VAR:
View/ Lag Structure/ Granger Causality

15.

VAR Granger Causality/Block Exogeneity Wald Tests
Sample: 1 500
Included observations: 499
Dependent variable: X
Excluded Chi-sq df
Prob.
Y
Z
All
0.6741
0.0000
0.0000
0.176851
42.75958
52.03015
1
1
2
Dependent variable: Y
Excluded Chi-sq
df
X
Z
All
0.087042
158.7880
188.9828
1
1
2
Prob.
0.7680
0.0000
0.0000
Dependent variable: Z
Excluded Chi-sq
df
Prob.
X
Y
All
0.0000
0.1948
0.0000
33.71340
1.680859
33.86982
1
1
2

16.

Группа 1: переменная Y
Группа 2: переменные X и Z
X = C(1)*X(-1) + C(2)*Y(-1) + C(3)*Z(-1)
Y = C(4)*X(-1) + C(5)*Y(-1) + C(6)*Z(-1)
Z = C(7)*X(-1) + C(8)*Y(-1) + C(9)*Z(-1)
c(2)=c(8)=0
(переменные X и Z блочно экзогенны по отношению к Y )
Wald Test:
System: SYS01
Test Statistic
Chi-square
Value
1.857710
df
2
Probability
0.3950

17. Нестабильные VAR

VAR нестабильна, если нарушено условие стабильности
Все корни уравнения
единичного круга.
det A(z)=0 лежат за пределами

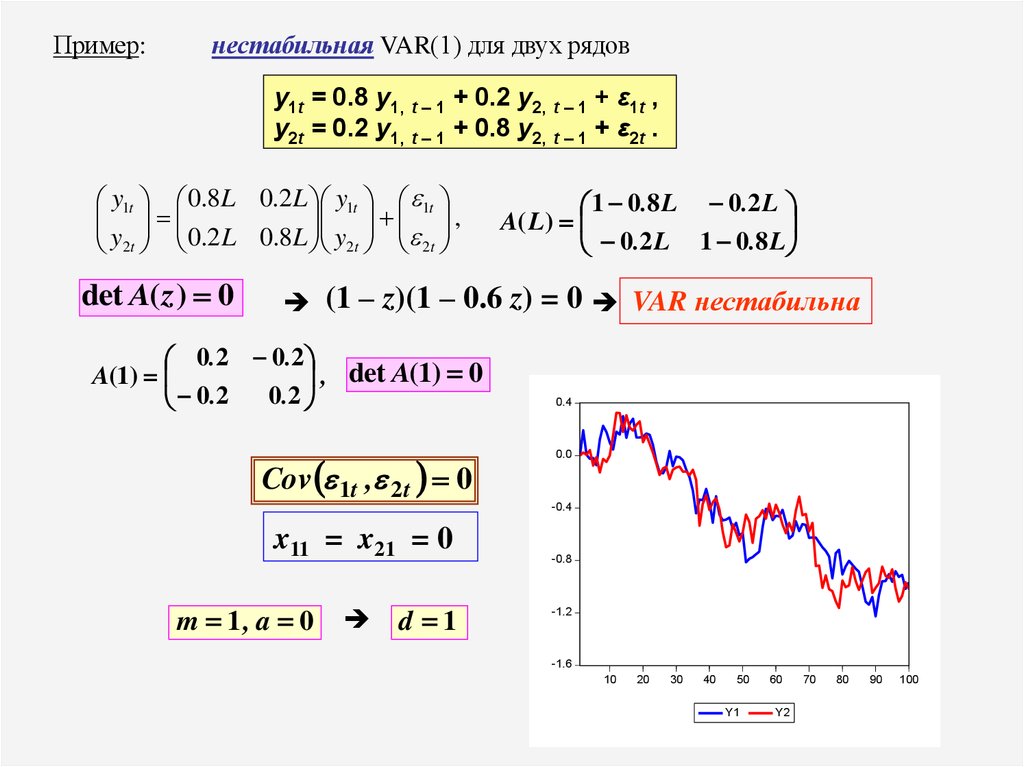
18.

Пример:
нестабильная VAR(1) для двух рядов
y1t = 0.8 y1, t – 1 + 0.2 y2, t – 1 + ε1t ,
y2t = 0.2 y1, t – 1 + 0.8 y2, t – 1 + ε2t .
y1t 0.8L 0.2 L y1t 1t
,
y2t 0.2 L 0.8L y2t 2t
det A( z ) 0
1 0.8 L 0.2 L
A( L)
0.2 L 1 0.8 L
(1 – z)(1 – 0.6 z) = 0 VAR нестабильна
0.2 0.2
, det A(1) 0
A(1)
0.2
0.2
Cov 1t , 2t 0
0.4
0.0
-0.4
x11 = x21 = 0
m 1, a 0
d 1
-0.8
-1.2
-1.6
10
20
30
40
50
Y1
60
Y2
70
80
90
100

19.

yt a1 yt 1 a 2 yt 2 t
yt a1 yt 1 a 2 yt 1 a 2 yt 1 a 2 yt 2 t
yt a1 yt 1 a 2 yt 1 a 2 yt 1 a 2 yt 2 t
yt a1 a 2 yt 1 a 2 yt 1 yt 2 t
y t y t 1 1 y t 1 t
a1 a 2
p 1 a2

20.

yt 1 yt 1 p yt p t
Компоненты вектора
yt
являются I(1)-рядами
Эквивалентная форма:
yt yt 1 1 yt 1 p 1 yt p 1 t
1 p
Если
I n , то компоненты yt
не коинтегрированы,
и модель принимает форму векторной авторегрессии VAR(p –1)
в разностях:
yt 1 yt 1 p 1 yt p 1 t

21.

DGP:
1 p I n
yt 1 yt 1 p 1 yt p 1 t
При оценивании статистической модели
yt yt 1 1 yt 1 p 1 yt p 1 t
независимо от того, 0 или 0 в DGP, совместное
распределение оценок матричных коэффициентов 1 , p 1
асимптотически нормально, так что для проверки гипотез об
этих коэффициентах можно использовать стандартные t и
F -критерии (в асимптотике), или
qF ~ 2 q .

22.

То же относится и к проверке гипотез о матричных коэффициентах
1 , , p в
yt 1 yt 1 p yt p t
кроме гипотез о значении их суммы 1 p .
(Оценка для этой суммы, т.е. для , имеет нестандартное
распределение.)
возможно использование стандартных тестов для
проверки гипотезы
H0: DGP=VAR(p0), p0 > 0,
против альтернативы
HA: DGP=VAR(p) c p > p0 ,
с целью выбора оптимальной глубины запаздываний.

23. Проверка на причинность по Грейнджеру отдельных переменных или подгруппы переменных в случае некоинтегрированной VAR

y it
Гипотеза H0 : переменные группы 2 не являются
Грейнджер-причиной для переменной группы 1.
В стационарном случае мы записывали модель в уровнях в виде
1Ti y t 1 1 T1i y t 21 2Ti y t 1 2 T2 i y t 2 2 Tpi y t 1 p Tpi y t 2 p i it
и проверяли гипотезу H 0 1i 2i
используя стандартные критерии.
Перепишем эту модель в виде:
pi 0,
yit i iT yt 1 1 iT yt 21 1Ti yt 1 1 1Ti yt 21 2Ti yt 1 2 2Ti yt 2 2
Tp 1 ,i yt 1 p 1 Tp 1 ,i yt 2 p 1 it .
нулевая гипотеза принимает вид:
H 0 : i 0 , 1i 2i p 1, i 0

24.

H 0 1i 2i pi 0
H 0 : i 0 , 1i 2i p 1, i 0
Cтатистика F -критерия для проверки гипотезы H0 численно
идентична статистике F -критерия для проверки гипотезы H0’.
Оценка для
i имеет нестандартное распределение
Cтатистика F -критерия для проверки гипотезы H0 имеет
нестандартное расределение.
Моделирование показывает, что в подобных ситуациях слишком
часто определяется ложная причинность по Грейнджеру.

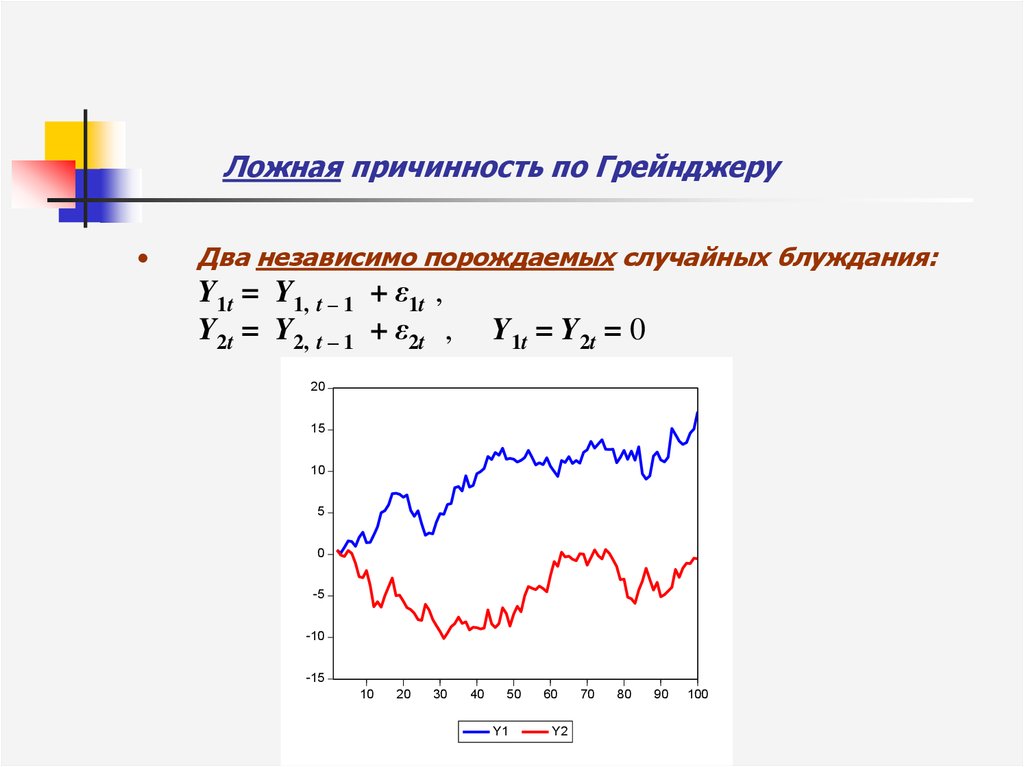
25. Ложная причинность по Грейнджеру

Два независимо порождаемых случайных блуждания:
Y1t = Y1, t – 1 + ε1t ,
Y2t = Y2, t – 1 + ε2t ,
Y1t = Y2t = 0
20
15
10
5
0
-5
-10
-15
10
20
30
40
50
Y1
60
Y2
70
80
90
100

26.

Проверка на причинность по Грейнджеру
Pairwise Granger Causality Tests
Sample: 1 100
Lags: 1
Null Hypothesis:
Obs F-Statistic
Y2 does not Granger Cause Y1 98
Y1 does not Granger Cause Y2
0.10520
5.93519
Prob.
0.7464
0.0167

27. Причинность в краткосрочном плане (short-run)

Если рассматривается некоинтегрированная VAR(p) с
I(1)-переменными, то, переходя к модели в разностях, мы
получаем стационарную VAR(p –1).
yt 1 yt 1 p 1 yt p 1 t
Если N=2, то VAR в разностях имеет вид:
(1)
(2)
( p 1 )
y1t 1 11
y1 ,t 1 11
y1 ,t 2 11
y1 ,t p 1
(1)
(2)
( p 1 )
12
y 2 ,t 1 12
y 2 ,t 2 12
y 2 ,t p 1 1t ,
(2)
( p 1 )
y 2 t 2 2( 11 ) y1 ,t 1 21
y1 ,t 2 21
y1 ,t p 1
(1)
(2)
( p 1 )
22
y 2 ,t 1 22
y 2 ,t 2 22
y 2 ,t p 1 2 t

28. Некоинтегрированная VAR: причинность в краткосрочном плане

Если в первом уравнении
(1)
(2)
( p 1 )
y1t 1 11
y1 ,t 1 11
y1 ,t 2 11
y1 ,t p 1
(1)
(2)
( p 1 )
12
y 2 ,t 1 12
y 2 ,t 2 12
y 2 ,t p 1 1t
(1)
(2)
( p 1)
12
12
12
0 ,
то
y2
плане.
не является G-причиной для
y1
в краткосрочном

29. Некоинтегрированная VAR: причинность в краткосрочном плане

Если во втором уравнении
(2)
( p 1 )
y2 t 2 2( 11 ) y1 ,t 1 21
y1 ,t 2 21
y1 ,t p 1
(1)
(2)
( p 1 )
22
y2 ,t 1 22
y2 ,t 2 22
y2 ,t p 1 2 t
(2)
( p 1)
2(1)
0
1
21
21
то
y1
плане.
не является G-причиной для
y2
в краткосрочном

30. Некоинтегрированная VAR: причинность в краткосрочном плане

В силу стационарности VAR в разностях,
асимптотически оправданно использование F-критериев для
проверки линейных гипотез о коэффициентах этой VAR,
так что проверка выполнения этих соотношений может
осуществляться на основе соответствующих F-критериев.

31. Проверка на причинность по Грейнджеру в случае коинтегрированной VAR

yt 1 yt 1 p yt p t
Модель
можно записать в форме модели коррекции ошибок
yt BAT yt 1 1 yt 1 p 1 yt p 1 t
B – N r -матрица коэффициентов адаптации,
AТ – r N -матрица, строки которой представляют r
линейно
независимых коинтегрирующих векторов-строк, r – ранг
коинтеграции , 1 r N 1 .
(При r = 0 коинтеграции нет ; при r = N все ряды стационарны.)

32.

y1t 1 B11 z1 ,t 1 B1r z r ,t 1
2
11
y1 ,t 2 1 ,2N y N ,t 2
p 1
11
y1 ,t p 1 1 ,pN 1 y N ,t p 1 1t ,
1
11
y1 ,t 1 1 1, N y N ,t 1
y Nt N B N 1 z1 ,t 1 B Nr z r ,t 1
N 21 y1 ,t 2 N 2, N y N ,t 2
N p1 1 y1 ,t p 1 N p, N1 y N ,t p 1 Nt
N 1 1 y1 ,t 1 N 1 , N y N ,t 1
z1 A1 yt 1 , , z r Ar yt 1 – стационарные линейные
комбинации (коинтегрирующие линейные комбинации)

33.

Коинтегрированная VAR
Обязательно должно выполняться условие
Xотя бы один из коэффициентов
B 0
Bij , i 1, N , j 1, , r ,
должен быть отличным от нуля.
Если отличен от нуля коэффициент Bij , то
в прогнозировании i-ой переменной помогают, во всяком
случае, прошлые значения тех переменных, у которых
коэффициенты в j-ой коинтегрирующей линейной
комбинации отличны от нуля.

34. Ситуация: Компоненты ряда yt являются I(1) рядами и ранг коинтеграции равен 1

Для оценивания модели коррекции ошибок можно использовать
двухступенчатую процедуру Энгла–Грейнджера
Производится OLS оценивание уравнения
y1t 2 y2 t 3 y3 t N y Nt ut
ˆ , ˆ 2 , ˆ 3 , , ˆ N
На основании полученных оценок
коэффициентов долговременного соотношения получают оценку
zˆ 1t y1t ˆ ˆ 2 y2t ˆ 3 y3t ˆ N y Nt
стационарной линейной комбинации
z1t y1t 2 y2t 3 y3t N y Nt
имеющей нулевое среднее.
Построенную переменную zˆ 1t подставляют вместо z1t в правую
часть уравнений системы в форме модели коррекции ошибок, и
производят OLS оценивание коэффициентов последней.

35. ЕСМ, полученная двухступенчатой процедурой Энгла–Грейнджера

Стандартные (асимптотические) процедуры проверки
гипотез о параметрах ECM могут применяться к любым
гипотезам, не включающим предположение
B11 B N 1 0
поскольку такое предположение соответствует
некоинтегрированности компонент ряда
yt .
При гипотезе H 0 : B11 B N 1 0 асимптотическое
распределение оценок коэффициентов B11 , , B N 1
–
нестандартное.

36. Коинтегрированная двумерная VAR

Ранг коинтеграции равен
1, так что ECM имеет вид
(1)
(1)
y1t 1 B11 z1 ,t 1 11
y1 ,t 1 12
y 2 ,t 1
(2)
(2)
11
y1 ,t 2 12
y 2 ,t 2
( p 1 )
( p 1 )
11
y1 ,t p 1 12
y 2 ,t p 1 1t ,
(1)
y 2 t 2 B21 z1 ,t 1 2( 11 ) y1 ,t 1 22
y 2 ,t 1
(2)
(2)
21
y1 ,t 2 22
y 2 ,t 2
( p 1 )
( p 1 )
21
y1 ,t p 1 22
y 2 ,t p 1 2 t
или

37. ECM для коинтегрированной двумерной VAR

y1t 1 B11 z1 ,t 1
(1)
(2)
( p 1 )
11
y1 ,t 1 11
y1 ,t 2 11
y1 ,t p 1
(1)
(2)
( p 1 )
12
y 2 ,t 1 12
y 2 ,t 2 12
y 2 ,t p 1 1t ,
y 2 t 2 B21 z1 ,t 1
(2)
( p 1 )
2( 11 ) y1 ,t 1 21
y1 ,t 2 21
y1 ,t p 1
(1)
(2)
( p 1 )
22
y 2 ,t 1 22
y 2 ,t 2 22
y 2 ,t p 1 2 t ,
где
z1 ,t 1 y1 ,t 1 2 y2 ,t 1
с
2 0

38. ECM для коинтегрированной двумерной VAR

Хотя бы один из коэффициентов
от нуля
B11 или B21 должен отличаться
в правую часть хотя бы одного из двух уравнений ECM
входит в качестве объясняющей переменная
z1 ,t 1 y1 ,t 1 2 y2 ,t 1
Но это означает, что в таком уравнении имеет место
причинность по Грейнджеру.

39. ECM для коинтегрированной двумерной VAR

Например, если в уравнении для
Δy1t имеем B11 0 , то
значение
y2,t – 1 помогает в прогнозировании значения y1t
наряду со значениями y1,t – 1 и y1 ,t 1 , y1 ,t 2 , , y1 ,t p 1 .
Фактически вопрос может стоять только о том, существует ли Gпричинность в выбранном направлении, например
в направлении от ряда
y2,t
к ряду
y1,t .
В последнем случае, гипотеза об отсутствии такой
причинности:
.
(1)
(2)
( p 1 )
H 0 : B11 0 , 12
12
12
0
Эту гипотезу можно проверить стандартными методами, даже
если использовать вместо значений z1t значения zˆ 1t
,
полученные применением процедуры Энгла – Грейнджера.

40. Причинность по Грейнджеру

Методология Тода – Ямамото
Выше было уже указано, как можно проводить проверку на
причинность по Грейнджеру, если
VAR стационарна
VAR состоит из I(1) рядов и они некоинтегрированы
(следует перейти к разностям для проверки наличия Gпричинности в краткосрочном плане)
VAR состоит из I(1) рядов и они коинтегрированы.

41.

Применение соответствующих методов требует
предварительной проверки гипотезы единичного корня
для определения порядков интегрированности рядов и
проверки гипотезы об их
коинтегрированности/некоинтегрированности.
Однако, критерии для проведения такой проверки обычно
обладают малой мощностью, и это ограничивает применение
указанных методов.
Тода и Ямамото ([Toda, Yamamoto (1995) ] предложили
процедуру, позволяющую обойти эти проверки.

42. Методология Тода – Ямамото

DGP :
y t 0 1 t q t q 1 y t 1 k y t k t
t ~ i. i. d . 0, ,
E it
2
для некоторого 0
Расширенная статистическая модель (augmented SM):
y t 0 1 t q t q 1 y t 1 k y t k p y t p t
p k d , d – порядок интегрированности ряда yt
где
В качестве
d
обычно берется предполагаемый максимальный
порядок интегрированности рядов в составе
yt .

43. Методология Тода – Ямамото

Гипотезы отсутствия причинности по Грейнджеру в DGP
затрагивают в такой постановке только элементы матриц
1 , , k и не затрагивают остальных матриц в SM,
т.е. матриц k 1 , , p .
Если гипотеза накладывает m линейных ограничений на
элементы матриц 1 , , k , то статистика Вальда для
проверки такой гипотезы имеет асимптотическое
распределение 2 m .
При этом ряд может быть стационарным, I(1) или I(2),
причем в каждом случае – еще и относительно линейного
тренда, и если он I(1) или I(2), то может быть и
коинтегрированным.

44. Методология Тода – Ямамото: Выбор количества лагов

DGP :
SM :
y t 0 1 t q t q 1 y t 1 k y t k t
y t 0 1 t q t q 1 y t 1 k y t k p y t p t ,
Гипотеза о невхождении в DGP лагов более высокого порядка, чем
H 0 : l 1 p 0
Если эта гипотеза верна и
k l
p 1
l d , то статистика Вальда для
проверки этой гипотезы имеет асимптотическое распределение
2 N 2 p l
l

45. Методология Тода – Ямамото: Выбор количества лагов

Если
k d , то l k d
Если порядки интегрированности рядов не превышают
истинное количество запаздываний в DGP, то применима
обычная процедура выбора количества лагов в VAR.
Если
Если
d = 2 , то
d = 1 , то
процедура выбора порядка модели
всегда асимптотически обоснованна.
она асимптотически обоснованна только при
При выборе порядка модели можно также использовать
информационные критерии.
k >1

46. Резюме:

При подозрениях на возможную интегрированность или
коинтегрированность рядов в составе yt , гипотезу H0
можно проверять, не производя проверки рядов на
интегрированность и коинтегрированность, а
лишь озаботясь тем, чтобы SM в виде VAR имела
порядок (k+ dmax ).
Используя стандартную асимптотическую теорию, можно
проверять и другие линейные (и многие нелинейные) ограничения
на первые
k
матриц коэффициентов.

47. Замечания

лагов может значительно понизить
мощность критериев, если количество рядов N велико.
Добавление
лишних
В модель можно также включать сезонные дамми.

48. Причинность в долгосрочном плане (long-run) и причинность в краткосрочном плане (short-run)

Если рассматривается некоинтегрированная VAR(p) с
I(1)-переменными, то, переходя к модели в разностях, мы
получаем стационарную VAR(p –1).
Если N=2, то VAR в разностях имеет вид:
(1)
(2)
( p 1 )
y1t 1 11
y1 ,t 1 11
y1 ,t 2 11
y1 ,t p 1
(1)
(2)
( p 1 )
12
y 2 ,t 1 12
y 2 ,t 2 12
y 2 ,t p 1 1t ,
(2)
( p 1 )
y 2 t 2 2( 11 ) y1 ,t 1 21
y1 ,t 2 21
y1 ,t p 1
(1)
(2)
( p 1 )
22
y 2 ,t 1 22
y 2 ,t 2 22
y 2 ,t p 1 2 t

49. Некоинтегрированная VAR: причинность в краткосрочном плане

Если в первом уравнении
(1)
(2)
( p 1 )
y1t 1 11
y1 ,t 1 11
y1 ,t 2 11
y1 ,t p 1
(1)
(2)
( p 1 )
12
y 2 ,t 1 12
y 2 ,t 2 12
y 2 ,t p 1 1t
(1)
(2)
( p 1)
12
12
12
0 ,
то
y2
плане.
не является G-причиной для
y1
в краткосрочном

50. Некоинтегрированная VAR: причинность в краткосрочном плане

Если во втором уравнении
(2)
( p 1 )
y2 t 2 2( 11 ) y1 ,t 1 21
y1 ,t 2 21
y1 ,t p 1
(1)
(2)
( p 1 )
22
y2 ,t 1 22
y2 ,t 2 22
y2 ,t p 1 2 t
(2)
( p 1)
2(1)
0
1
21
21
то
y1
плане.
,
не является G-причиной для
y2
в краткосрочном

51.

Коинтегрированная VAR:
причинность в краткосрочном и в долгосрочном плане
Если N=2, то соответствующая ECM имеет вид:
y1t 1 B11 z1 ,t 1
(1)
(2)
( p 1 )
11
y1 ,t 1 11
y1 ,t 2 11
y1 ,t p 1
(1)
(2)
( p 1 )
12
y 2 ,t 1 12
y 2 ,t 2 12
y 2 ,t p 1 1t ,
y 2 t 2 B21 z1 ,t 1
(2)
( p 1 )
2( 11 ) y1 ,t 1 21
y1 ,t 2 21
y1 ,t p 1
(1)
(2)
( p 1 )
22
y 2 ,t 1 22
y 2 ,t 2 22
y 2 ,t p 1 2 t

52.

Коинтегрированная VAR:
причинность в краткосрочном и в долгосрочном плане
В рамках этой ECM можно проверять как гипотезы об отсутствии
краткосрочной G-причинности одной из переменных в
отношении другой, выражаемые соотношениями
(1)
(2)
( p 1)
12
12
12
0
и
(2)
( p 1)
2(1)
0
1
21
21
так и гипотезы об отсутствии долговременной G-
причинности одной из переменных в отношении другой
выражаемые соотношениями
B11= 0 и B21=0, соответственно
При этом, гипотеза об отсутствии G-причинности в
выбранном направлении, например, в направлении от y2 к y1 ,
формулируется, как это уже было сделано ранее:
(1)
(2)
(p 1)
H 0 : B11 0 , 12
12
12
0

53.

К методу Тода-Ямамото

54.

Если мы имеем дело с векторным временным рядом, то
такой временной ряд называется интегрированным порядка
векторный ряд
d , если:
Δd yt стационарный и в представлении
d yt C L t
C 1
Ci 0
i 0
Но на сей раз
C(1) – матрица, поэтому для выполнении последнего условия
достаточно иметь хотя бы один отличный от нуля элемент матрицы C(1),
а остальные элементы этой матрицы могут быть нулями.
Соответственно, у интегрированного порядка
ряда должна быть хотя бы одна
d
векторного временного
I(d) компонента, а остальные
компоненты могут иметь порядки I(k) , k < d .

55.

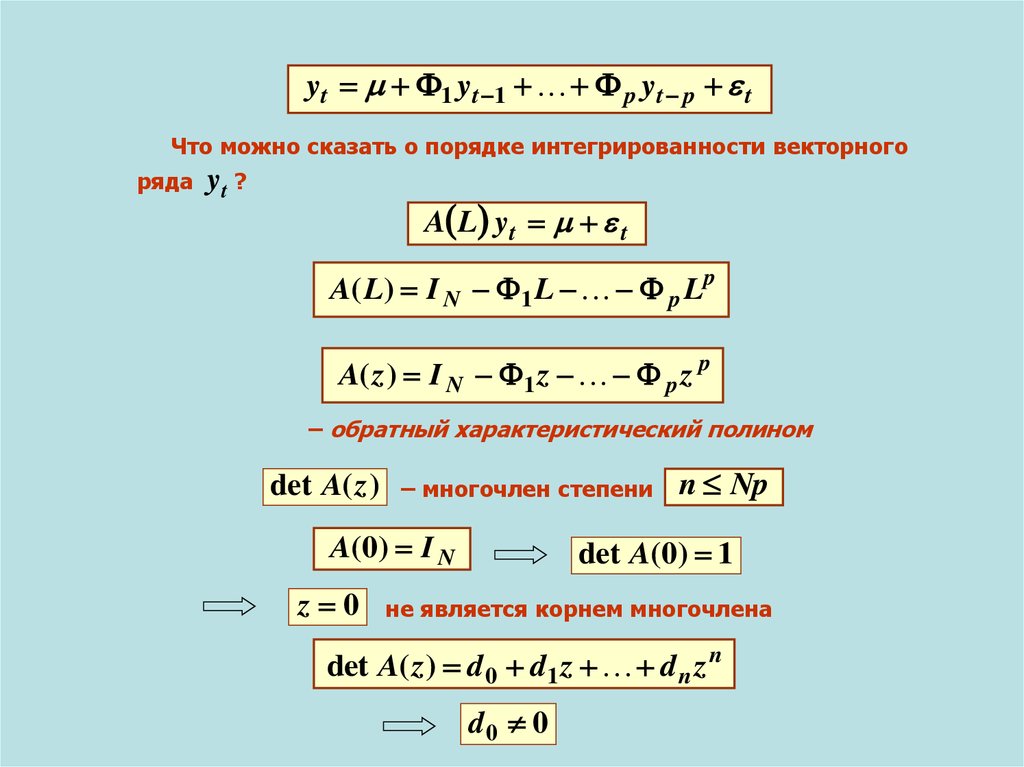
yt 1 yt 1 p yt p t
Что можно сказать о порядке интегрированности векторного
ряда
yt ?
A L yt t
A( L) I N 1 L p Lp
A( z ) I N 1 z p z p
– обратный характеристический полином
det A( z )
– многочлен степени
A(0) I N
z 0
n Np
det A(0) 1
не является корнем многочлена
det A( z ) d 0 d1 z d n z n
d0 0

56.

det A( z ) d 0 d1 z d n z n
Тогда можно записать:
nr
det A( z ) d n z z i mi z 1 m g z
i 1
где
g 1 0
так что многочлен
1 m n
det A( z )
имеет
m единичных корней.
Если бы мы имели дело с одномерным временным рядом, то
отсюда следовало бы, что
m – порядок интегрированности ряда.
В случае векторного временного ряда положение сложнее.

57.

Пусть
A (z )
А( z )
1
– присоединенная матрица для
A ( z )
А( z )
Пусть многочлен
единичного круга.
A(z )
, так что
если обратная матрица существует
det A( z )
не имеет корней внутри
Тогда порядок интегрированности ряда
yt
равен
d m a
где значение
a
определяется соотношением
A ( z ) z 1 a H z , H 1 0
MASSIMO FRANCHI (2006)
“THE INTEGRATION ORDER OF VECTOR AUTOREGRESSIVE PROCESSES”

58.

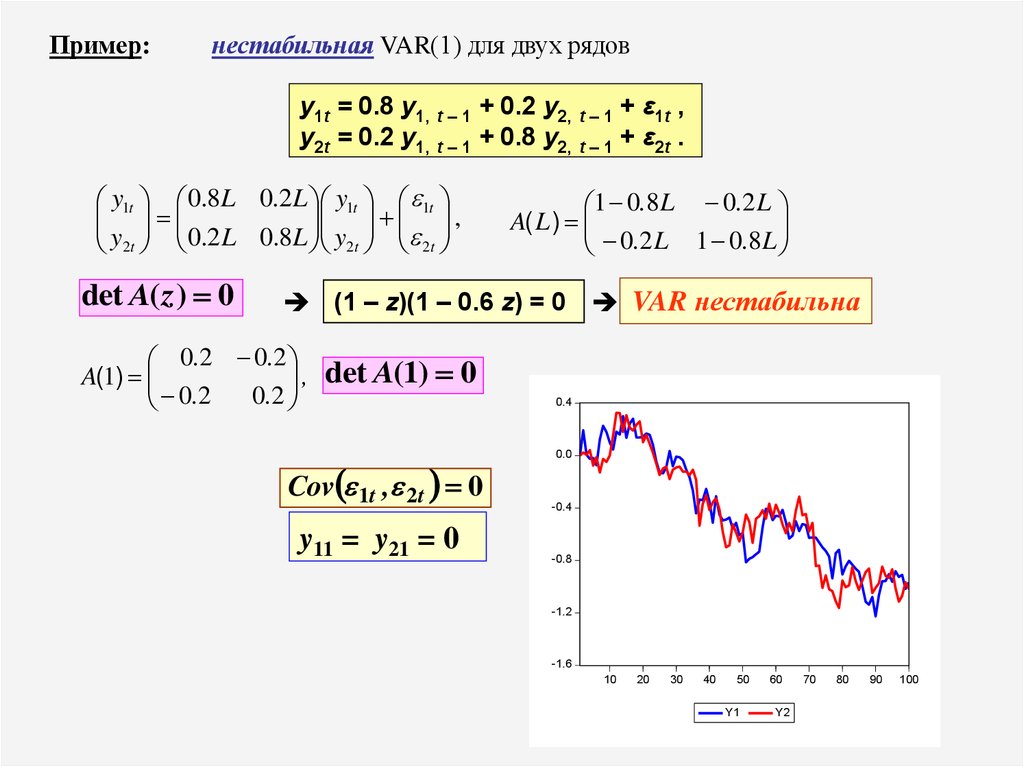
Пример:
нестабильная VAR(1) для двух рядов
y1t = 0.8 y1, t – 1 + 0.2 y2, t – 1 + ε1t ,
y2t = 0.2 y1, t – 1 + 0.8 y2, t – 1 + ε2t .
y1t 0.8L 0.2 L y1t 1t
,
y2t 0.2 L 0.8L y2t 2t
det A( z ) 0
1 0.8L 0.2 L
A( L )
0
.
2
L
1
0
.
8
L
(1 – z)(1 – 0.6 z) = 0 VAR нестабильна
0.2 0.2
A(1)
,
0.2
0.2
det A(1) 0
Cov 1t , 2t 0
y11 = y21 = 0
0.4
0.0
-0.4
-0.8
-1.2
-1.6
10
20
30
40
50
Y1
60
Y2
70
80
90
100

59.

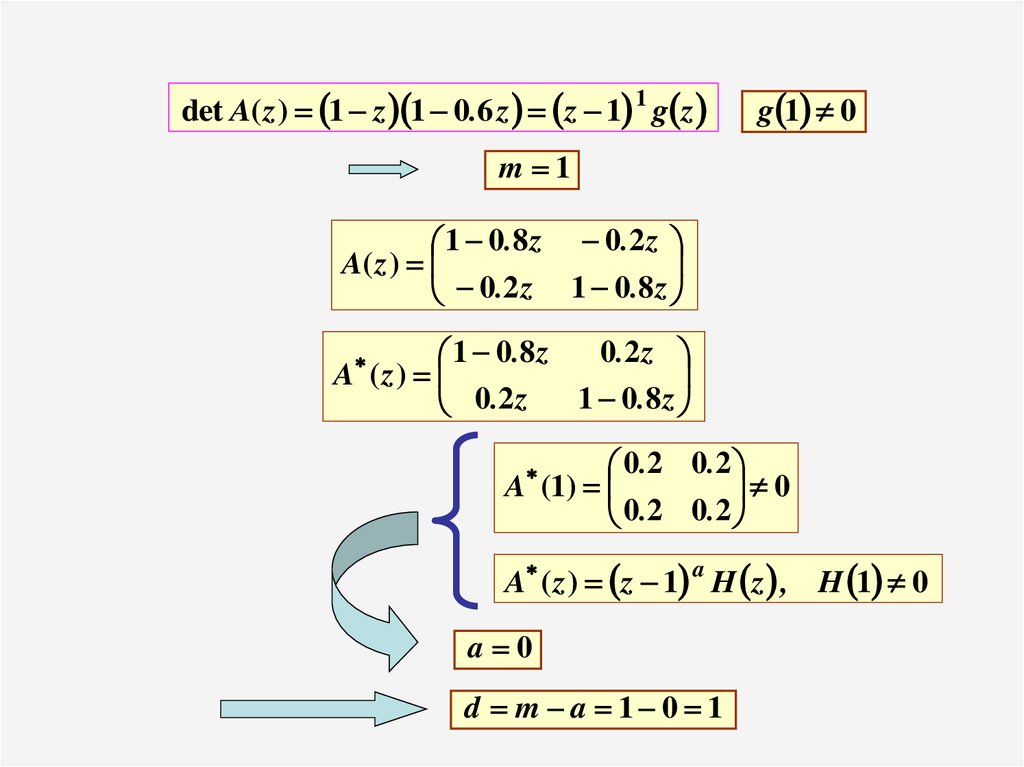
det A( z ) 1 z 1 0.6 z z 1 1 g z
g 1 0
m 1
1 0 .8 z 0 . 2 z
A( z )
0 .2 z 1 0 . 8 z
0 .2 z
1 0 .8 z
A (z)
1 0 .8 z
0 .2 z
0 . 2 0 .2
A (1)
0
0 . 2 0 .2
A ( z ) z 1 a H z , H 1 0
a 0
d m a 1 0 1

60.

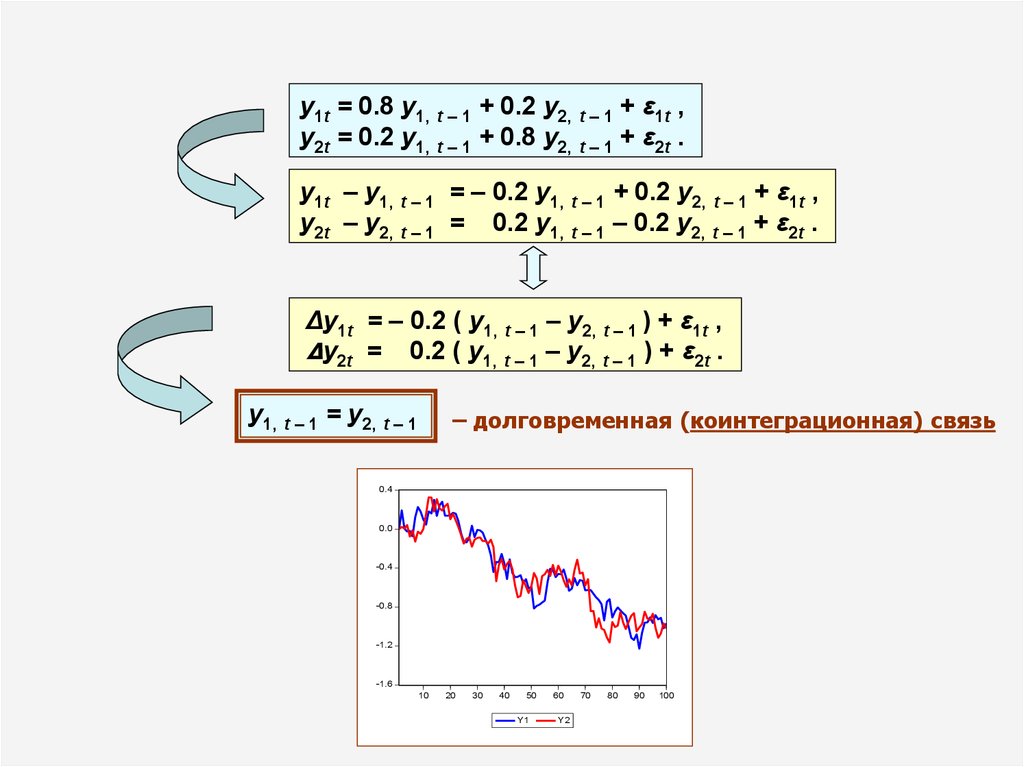
y1t = 0.8 y1, t – 1 + 0.2 y2, t – 1 + ε1t ,
y2t = 0.2 y1, t – 1 + 0.8 y2, t – 1 + ε2t .
y1t – y1, t – 1 = – 0.2 y1, t – 1 + 0.2 y2, t – 1 + ε1t ,
y2t – y2, t – 1 = 0.2 y1, t – 1 – 0.2 y2, t – 1 + ε2t .
Δy1t = – 0.2 ( y1, t – 1 – y2, t – 1 ) + ε1t ,
Δy2t = 0.2 ( y1, t – 1 – y2, t – 1 ) + ε2t .
y1, t – 1 = y2, t – 1
– долговременная (коинтеграционная) связь
0.4
0.0
-0.4
-0.8
-1.2
-1.6
10
20
30
40
50
Y1
60
Y2
70
80
90
100