Similar presentations:
Вычисление площади многоугольника
1. Вычисление площади многоугольника
Городская научно-практическая конференция юных исследователей«Будущее Петрозаводска»
Вычисление площади
многоугольника
Качановская Алина Игоревна
МОУ «Гимназия №30 имени Музалева Д.Н.»,
9Б класс, г. Петрозаводск.
Руководитель Орлова Ирина Анатольевна
учитель математики
МОУ «Гимназия №30 имени Музалева Д.Н.»
2. Вычисление площади многоугольника
Гипотеза.Используя координатный метод и формулу Пика, можно сократить время
для вычисления площади многоугольника.
Объект исследования – площадь многоугольника.
Предмет исследования – способы нахождения площади многоугольника.
Цель исследования: изучить методы вычисления площади по координатам
вершин и с помощью формулы Пика и научиться применять их на практике.
Задачи:
• изучить теоретический материал по данной теме;
• вывести формулы вычисления площади по координатам;
• на практике применить данные способы для вычисления площадей
многоугольников;
• сравнить результаты нахождения площади многоугольников разными
способами.
Методы исследования: изучение литературы и Интернет-ресурсов,
сравнение, обобщение, аналогия.
3. Вычисление площади многоугольника по координатам его вершин
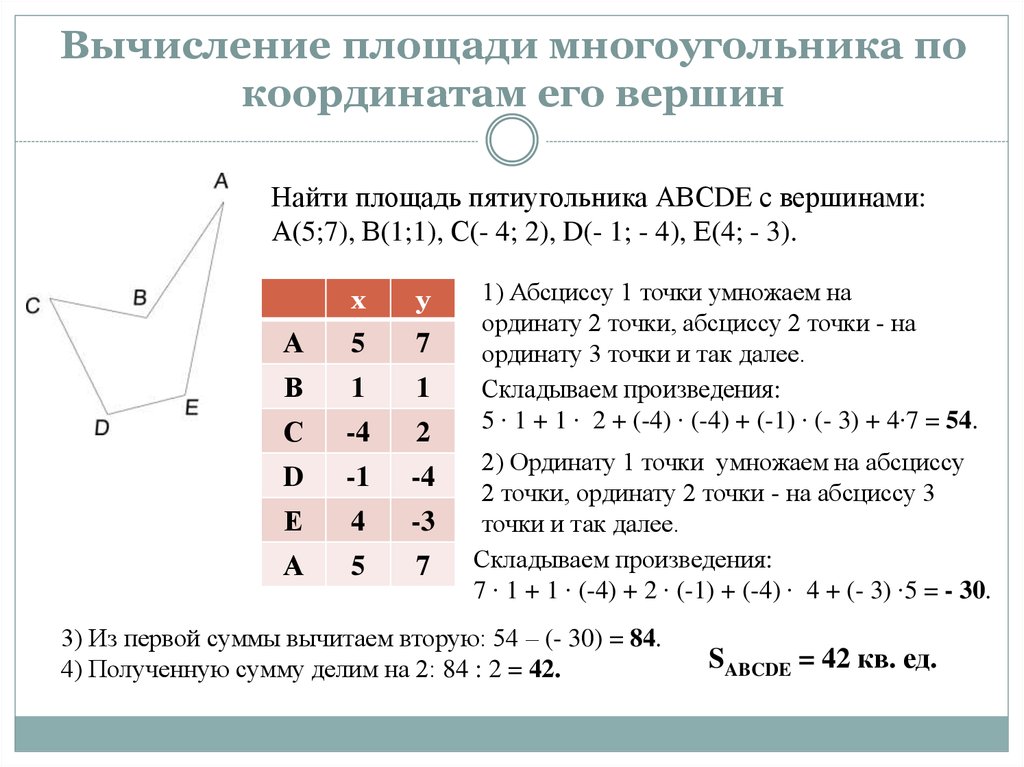
Найти площадь пятиугольника АВСDE с вершинами:А(5;7), В(1;1), С(- 4; 2), D(- 1; - 4), Е(4; - 3).
х
у
А
5
7
В
1
1
С
-4
2
D
-1
-4
Е
4
-3
А
5
7
1) Абсциссу 1 точки умножаем на
ординату 2 точки, абсциссу 2 точки - на
ординату 3 точки и так далее.
Складываем произведения:
5 ∙ 1 + 1 ∙ 2 + (-4) ∙ (-4) + (-1) ∙ (- 3) + 4∙7 = 54.
2) Ординату 1 точки умножаем на абсциссу
2 точки, ординату 2 точки - на абсциссу 3
точки и так далее.
Складываем произведения:
7 ∙ 1 + 1 ∙ (-4) + 2 ∙ (-1) + (-4) ∙ 4 + (- 3) ∙5 = - 30.
3) Из первой суммы вычитаем вторую: 54 – (- 30) = 84.
4) Полученную сумму делим на 2: 84 : 2 = 42.
SABCDE = 42 кв. ед.
4. Вычисление площади треугольника
ху
А1
х1
у1
А2
х2
у2
А3
х3
у3
А1
х1
у1
Треугольник А1А2А3 с координатами
вершин (х1, у1), (х2,у2) и (х3, у3).
S 0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 )
Равенство 1
5. Вычисление площади треугольника
.S A1 A2 A3 S A2 A1B1B2 S A2 A3 B3 B2 S A3 A1B1B3
(равенство 2)
Так как А1А2В2В1 трапеция, то
S = 0,5(А2В2 + А1В1) ∙ В2В1
S A2 A1B1B2 0,5 y2 y1 x1 x2 .
S A2 A3 B3 B2 0,5 y 2 y 3 x3 x 2 и
S A3 A1B1B3 0,5 y3 y1 x1 x3 .
Выполним алгебраические преобразования
S А1 А2 А3 0,5 у 2 у1 х1 х 2 0,5 у 2 у3 х3 х 2 0,5 у1 у 3 х1 х3
0,5 у 2 х1 0,5 у 2 х2 0,5 у1 х1 0,5 у1 х2 0,5 у 2 х3 0,5 у 2 х2 0,5 у3 х3 0,5 у3 х2 0,5 у3 х1
0,5 у3 х3 0,5 у1 х1 0,5х3 у1 0,5 х1 у 2 х2 у3 х3 у1 0,5 у1 х2 у 2 х3 у3 х1
0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .
6. Вычисление площади треугольника
.S A1 A2 A3 S A2 A3 B3 B2 S A2 A1B1B2 S A1 A3 B3 B1
(равенство 3)
S A2 A3 B3 B2 0,5 y 2 y 3 x3 x 2
S A2 A1B1B2 0,5 y 2 y1 x1 x 2
S A3 A1B1B3 0,5 y 3 y1 x3 x1
Выполним алгебраические преобразования
S А1 А2 А3 0,5 у 2 у3 х3 х 2 0,5 у 2 у1 х1 х 2 0,5 у1 у 3 х3 х1
0,5 у 2 х3 0,5 у 2 х2 0,5 у3 х3 0,5 у3 х2 0,5 у 2 х1 0,5 у 2 х2 0,5 у1 х1 0,5 у1 х2 0,5 у1 х3
0,5 у1 х1 0,5 у3 х3 0,5х1 у3 0,5 х1 у 2 х2 у3 х3 у1 0,5 у1 х2 у 2 х3 у3 х1
0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .
7. Вычисление площади треугольника
Если вершины треугольника взяты против часовой стрелки, тоS 0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .
Если вершины треугольника взяты по часовой стрелке, то
S 0,5 ( x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 ) .
S 0,5 | x1 y2 x2 y3 x3 y1 y1 x2 y2 x3 y3 x1 |
8. ΔАВС, А(- 3; 2), В(4,5; 0,8), С(1,8; -3,5)
Ах
у
А
-3
2
С
4,5
0,8
В
1,8
-3,5
А
-3
2
В
С
S=0,5((-3∙0,8+4,5∙(-3,5)+(1,8∙2)) –
– (2∙4,5+0,8∙1,8+(-3,5) ∙(-3))=17,745
9. Вычисление площади четырехугольника
.S A1 A2 A3 А4 S A1 A2 А4 S A2 A3 А4
S А1 А2 А4 0,5 ( x1 y 2 x 2 y 4 x 4 y1 y1 x 2 y 2 x 4 y 4 x1 )
S А2 А3 А4 0,5 ( x 2 y3 x3 y 4 x 4 y 2 y 2 x3 y 3 x 4 y 4 x 2 )
Выполним алгебраические преобразования
S A1 A2 A3 А4 0,5 х1 у 2 0,5 х 2 у 4 0,5 х 4 у1 0,5 у1 х 2 0,5 у 2 х 4 0,5 у 4 х1 0,5 х 2 у3 0,5 х3 у 4
0,5х4 у 2 0,5 у 2 х3 0,5 у3 х4 0,5 у 4 х2 0,5( х1 у 2 х2 у3 х3 у 4 х4 у1 ) 0,5( у1 х2 у 2 х3
у3 х4 у 4 х1 )
S 0,5 ( x1 y 2 x2 y3 x3 y 4 х4 у1 y1 x2 y 2 x3 y3 x4 у 4 х1 )
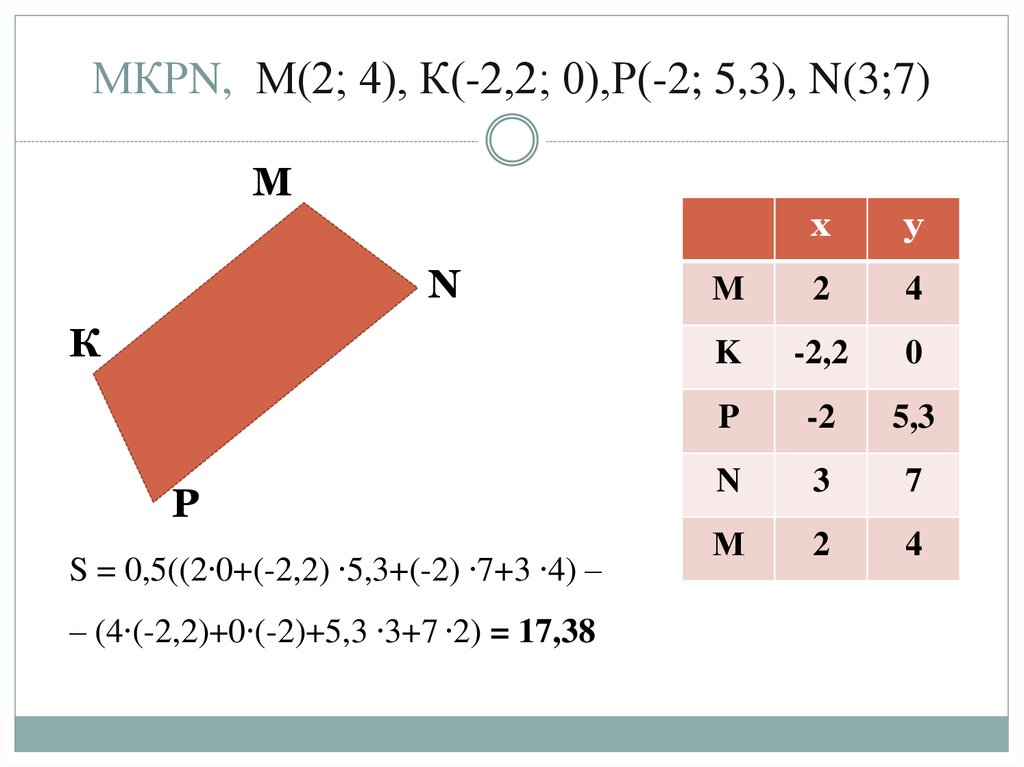
10. МКРN, М(2; 4), К(-2,2; 0),Р(-2; 5,3), N(3;7)
МN
К
Р
S = 0,5((2∙0+(-2,2) ∙5,3+(-2) ∙7+3 ∙4) –
– (4∙(-2,2)+0∙(-2)+5,3 ∙3+7 ∙2) = 17,38
x
y
M
2
4
K
-2,2
0
P
-2
5,3
N
3
7
М
2
4
11. Алгоритм вычисления площади много- угольника по координатам его вершин
Алгоритм вычисления площади многоугольника по координатам его вершинх
у
А1
х1
у1
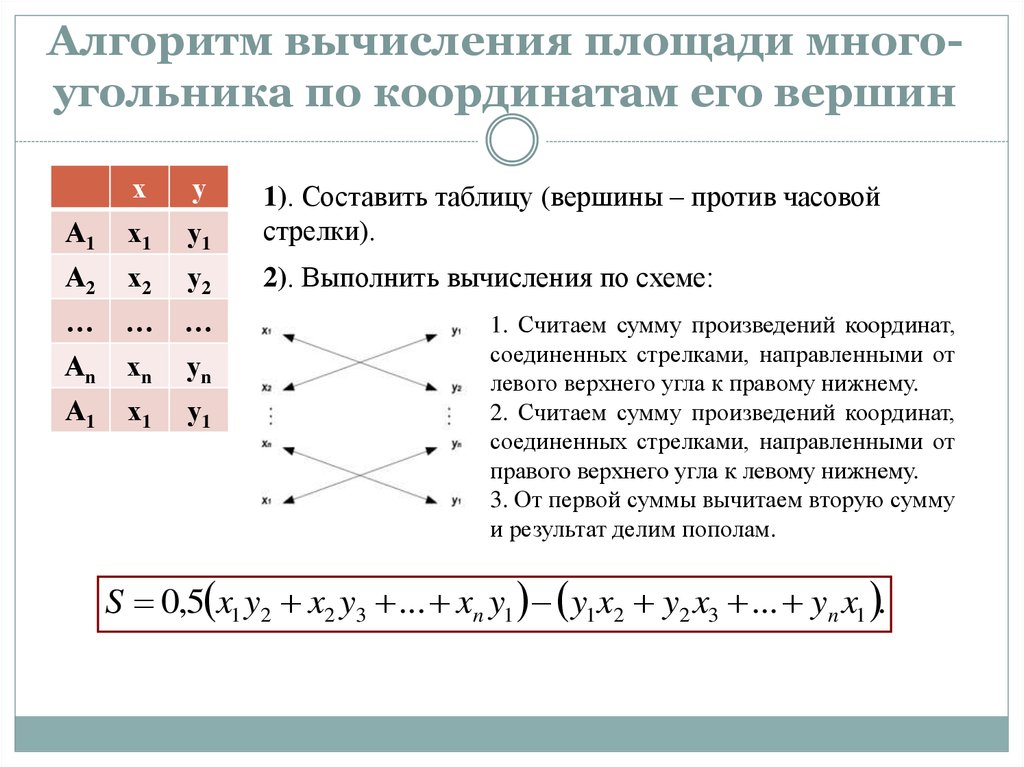
1). Составить таблицу (вершины – против часовой
стрелки).
А2
х2
у2
2). Выполнить вычисления по схеме:
…
…
…
Аn
хn
уn
А1
х1
у1
1. Считаем сумму произведений координат,
соединенных стрелками, направленными от
левого верхнего угла к правому нижнему.
2. Считаем сумму произведений координат,
соединенных стрелками, направленными от
правого верхнего угла к левому нижнему.
3. От первой суммы вычитаем вторую сумму
и результат делим пополам.
S 0,5 x1 y2 x2 y3 ... xn y1 y1 x2 y2 x3 ... yn x1 .
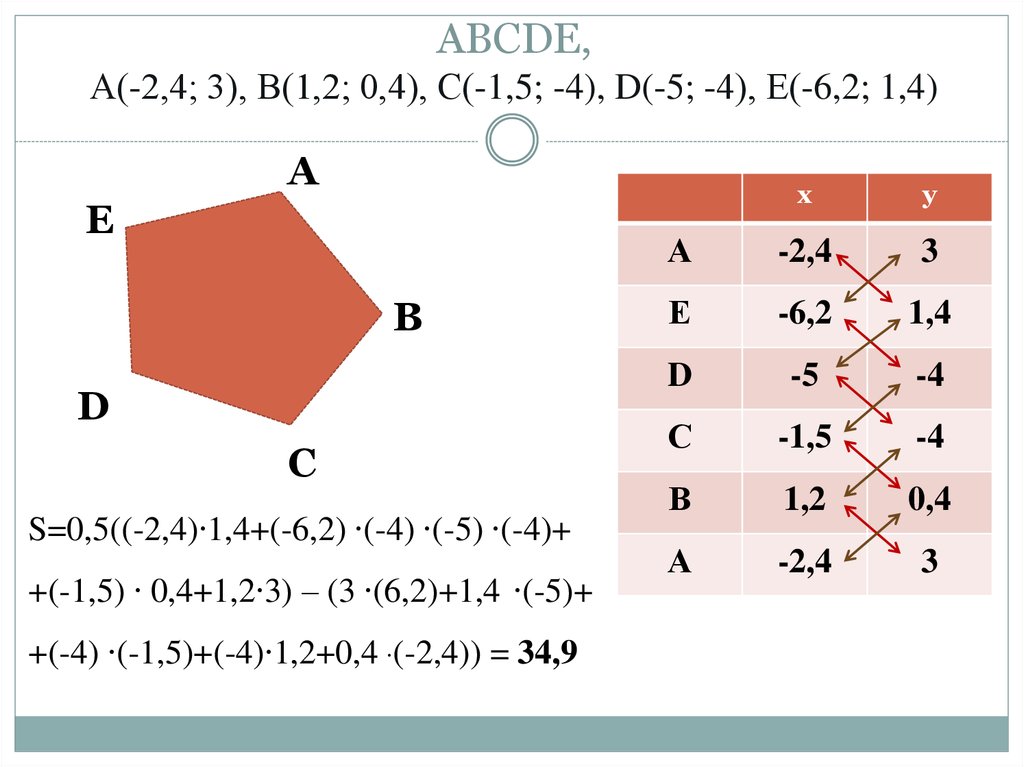
12. АВСDE, А(-2,4; 3), В(1,2; 0,4), С(-1,5; -4), D(-5; -4), Е(-6,2; 1,4)
АЕ
В
D
С
S=0,5((-2,4)∙1,4+(-6,2) ∙(-4) ∙(-5) ∙(-4)+
+(-1,5) ∙ 0,4+1,2∙3) – (3 ∙(6,2)+1,4 ∙(-5)+
+(-4) ∙(-1,5)+(-4)∙1,2+0,4 ∙(-2,4)) = 34,9
х
у
А
-2,4
3
Е
-6,2
1,4
D
-5
-4
С
-1,5
-4
В
1,2
0,4
А
-2,4
3
13. Вычисление площади многоугольников по формуле Пика
Площадь многоугольника, изображенного наклетчатой бумаге:
Г
S В 1
2
Георг Пик
(1859 – 1942)
Г – количество целочисленных точек на границе
многоугольника,
В – количество целочисленных точек внутри
многоугольника.
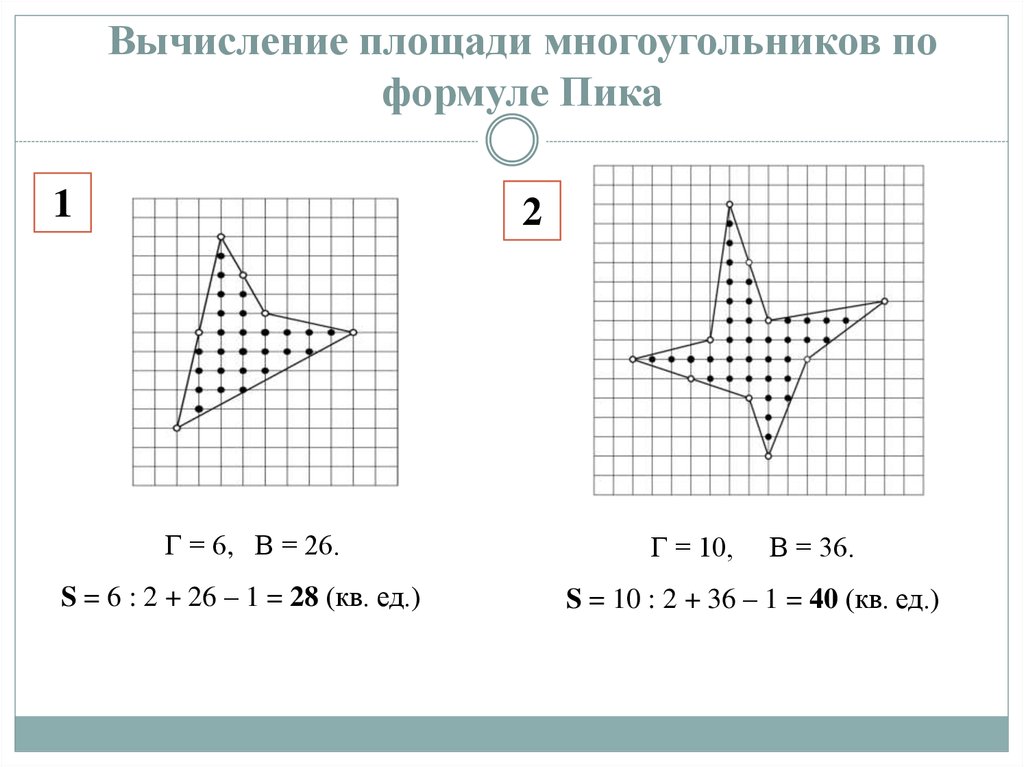
14. Вычисление площади многоугольников по формуле Пика
12
Г = 6, В = 26.
S = 6 : 2 + 26 – 1 = 28 (кв. ед.)
Г = 10,
В = 36.
S = 10 : 2 + 36 – 1 = 40 (кв. ед.)
15. Вычисление площади многоугольников разными способами
Площадь треугольника АВС• Достраивание
• По формуле Пика
• По координатам вершин
S = 20 кв. ед.
16. Вычисление площади многоугольников разными способами
Площадь выпуклогочетырехугольника АВСD
• Достраивание
• По формуле Пика
• По координатам вершин
• Разбиение
S = 40 кв. ед.
17. Вычисление площади многоугольников разными способами
Площадь невыпуклогочетырехугольника АВСD
• Достраивание
• По формуле Пика
• Разбиение
• По координатам его вершин
S = 15 кв. ед.
18. Вычисление площади многоугольников разными способами
Площадь невыпуклогосемиугольника АВСDЕКМ
• Достраивание
• По формуле Пика
• По координатам его вершин
S = 47,5 кв. ед.
19. Вычисление площади многоугольника
• Представлены два способа вычисления площади многоугольника:по координатам его вершин и по формуле Пика.
• Выведена формула для вычисления площади треугольника по
координатам его вершин.
• Выведена формула для вычисления площади четырехугольника по
координатам его вершин.
• Приведены примеры вычисления площадей многоугольников по
координатам их вершин.
• Приведены примеры вычисления площадей многоугольников по
формуле Пика.
• Приведены примеры вычисления площади одного и того же
многоугольника разными способами.
20. Вычисление площади многоугольника
Городская научно-практическая конференция юных исследователей«Будущее Петрозаводска»
Вычисление площади
многоугольника
Качановская Алина Игоревна
МОУ «Гимназия №30 имени Музалева Д.Н.»,
9Б класс, г. Петрозаводск.
Руководитель Орлова Ирина Анатольевна
учитель математики
МОУ «Гимназия №30 имени Музалева Д.Н.»















 mathematics
mathematics








