Основы биомеханники и биоакустики. (Лекция 3)

1. Основы биомеханики и биоакустики

ГУ «Луганский государственный
медицинский университет»
Основы биомеханики
и биоакустики
Лектор: к.т.н. Якимов А.Н.
Луганск - 2013

2. Введение

2
Механика ‒ это раздел физики, изучающий
движение и равновесие тел, вызванное их
взаимодействием.
Основные разделы механики:
• статика (равновесие тел)
• кинематика (движение тел)
• динамика (взаимодействие тел)
Вся механика основывается на трех законах,
открытых в 17-18 веках английским математиком,
астроном и физиком Исааком Ньютоном.

3. I. Законы Ньютона

3
1 ЗАКОН НЬЮТОНА
Если на тело не действуют силы или их
равнодействующая равна нулю, то тело находится
в состоянии покоя или движется прямолинейно с
постоянной скоростью.
если F 0 или Fi 0, то v 0 или v const
Этот закон часто называют законом инерции, а
прямолинейное движение, имеющее место при
отсутствии внешних сил ‒ движением по инерции.

4. Примеры

4
Примеры
1. Тело, висящее на нити
Fi Fн Fт 0 v 0
Fн Fт 0 ,
Fн Fт mg
Fн
Fт
2. Движение планет вокруг Солнца
Fi Fцб Fцс 0 v const (v const)
Эйнштейн показал, что вращение планет ‒ это также движение
тел по инерции, но в искривленном пространстве-времени.

5.

2 ЗАКОН НЬЮТОНА
5
Ускорение тела, вызываемое некоторой силой,
прямо пропорционально величине приложенной
силы и обратно пропорционально массе тела.
F
F m a a
m
Ускорение при равноускоренном прямолинейном
движении определяется по формуле
v v0
a
t
2
Единицы измерения: [ F ] H , [a] м / с , [m] кг

6. Одномерное прямолинейное движение с постоянным и переменным ускорением

v, a
x
a 0
S v t
Путь
Скорость
Ускорение
a const
a t
S v0 t
2
a const
2
t
S v dt
t0
S
v
t
v v0 a t
dx
v
x
dt
a 0
v v0 v
a
t t0 t
d 2x
a 2 x
dt
Второй закон Ньютона: m x F
6

7.

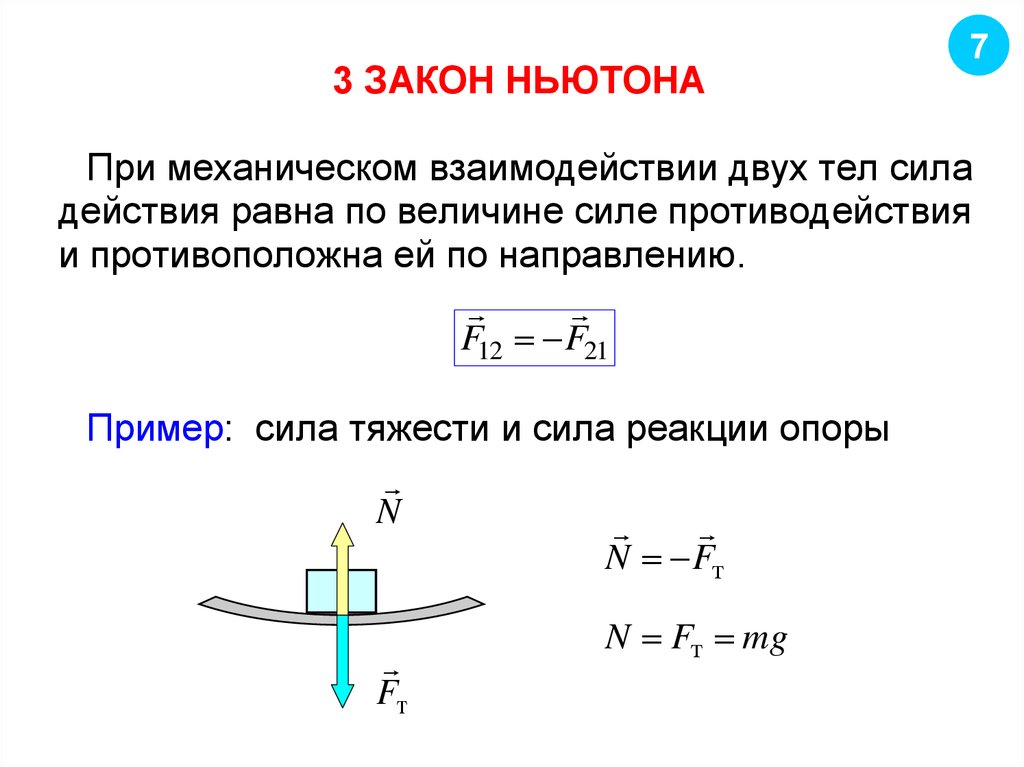
3 ЗАКОН НЬЮТОНА
7
При механическом взаимодействии двух тел сила
действия равна по величине силе противодействия
и противоположна ей по направлению.
F12 F21
Пример: сила тяжести и сила реакции опоры
N
N Fт
Fт
N Fт mg

8. II. Механические колебания

8
Значительная часть физических явлений связана
с колебательными и волновыми процессами.
В физике различают механические и электромагнитные колебания и волны.
Законы, описывающие механические колебания,
лежат в основе таких биологических процессов
как биение сердца, распространения нервного
импульса и пульсовой волны.
def Механическими колебаниями называются
движения тел, характеризующиеся той или
иной степенью повторяемости через
определенные промежутки времени.

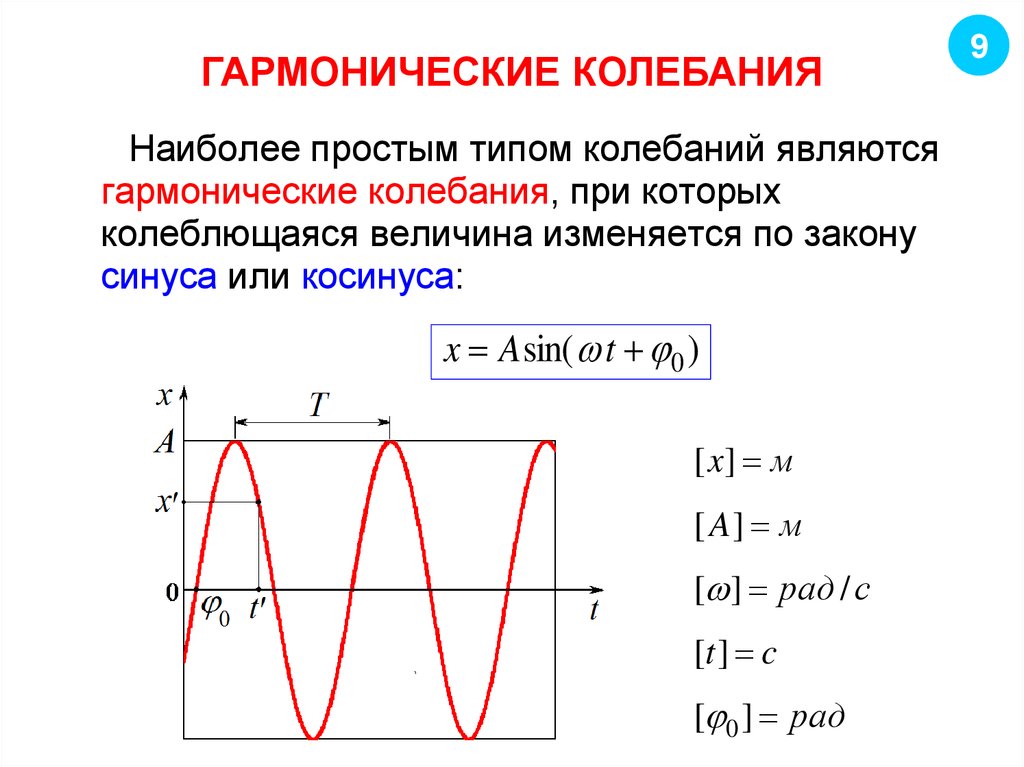
9. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Наиболее простым типом колебаний являются
гармонические колебания, при которых
колеблющаяся величина изменяется по закону
синуса или косинуса:
x A sin( t 0 )
[ x] м
[ A] м
[ ] рад / с
[t ] c
[ 0 ] рад
9

10. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ

10
Основные характеристики гармонических колебаний:
1) отклонение, или смещение x, от положения
равновесия;
2) амплитуда A колебания ‒ максимальное
отклонение от положения равновесия;
3) период T ‒ длительность одного полного колебания;
4) частота ‒ число колебаний в единицу времени,
1
1
v , [v] Гц
T
с
5) круговая, или циклическая, частота ,
2 v , [ ] рад / с
6) фаза колебаний : t 0 , [ ] рад

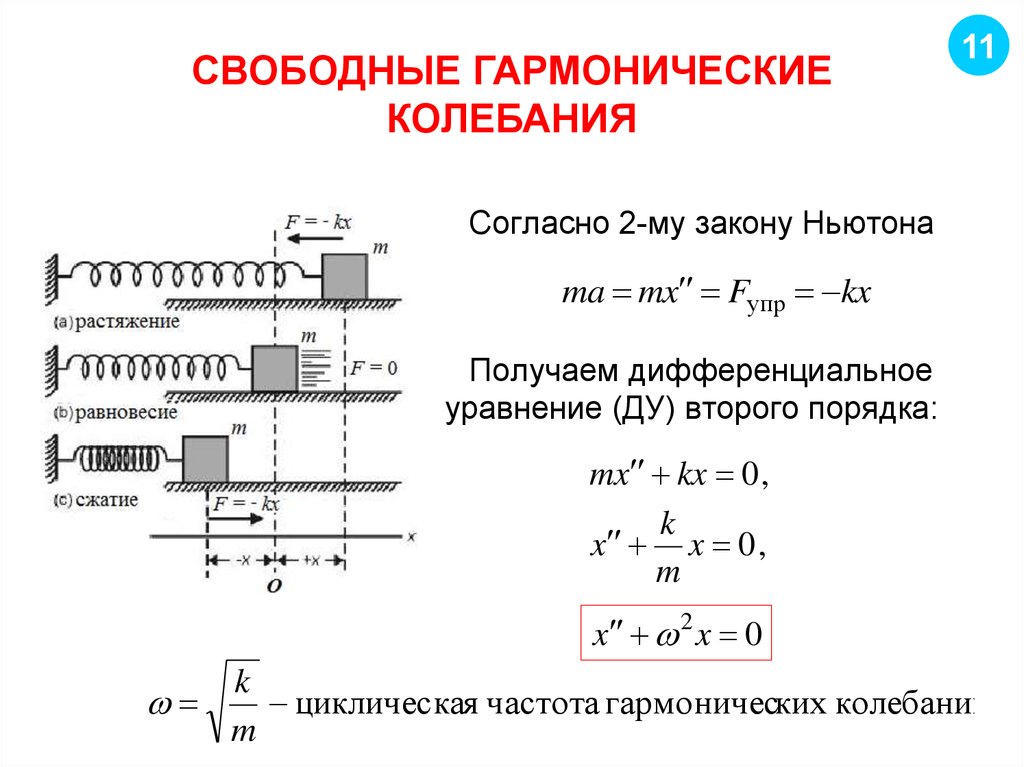
11. СВОБОДНЫЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

11
Согласно 2-му закону Ньютона
ma mx Fупр kx
Получаем дифференциальное
уравнение (ДУ) второго порядка:
mx kx 0 ,
k
x x 0 ,
m
x 2 x 0
k
циклическая частота гармонических колебаний
m

12. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

ОДУ 2-го порядка с постоянными коэффициентами
a y b y c y 0
Характеристическое уравнение: a 2 b c 0
D b2 4 a c
1) D > 0 (два корня):
1,2 его корни
y C1e 1x C2e 2 x
x
y
C
e
C2
2) D = 0 (один корень):
1
3) D < 0 ( 1,2 a ib ): y ea x (C1 cos b x C2 sin b x)
12

13. РЕШЕНИЕ ДУ СВОБОДНЫХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

13
x 2 x 0
Характеристическое уравнение: 2 2 0
D b 2 4ac 02 4 1 2 4 2 0
Его комплексные корни
b D
0
4 2
1,2
i , где i 1
2a
2 1
2 1
В нашем случае a 0, b , поэтому его
решение x e0 (C1 cos t C2 sin t ) A sin( t 0 )

14. СКОРОСТЬ И УСКОРЕНИЕ ПРИ СВОБОДНЫХ ГАРМОНИЧЕКИХ КОЛЕБАНИЯХ

Смещение:
x A sin( t 0 )
Скорость:
dx
v x
A cos( t 0 )
dt
Ускорение:
dv
a v
A 2 sin( t 0 )
dt
vmax A , amax A 2
14

15. ЭНЕРГИЯ СВОБОДНЫХ ГАРМОНИЧЕКИХ КОЛЕБАНИЙ

15
Полная энергия гармонических колебаний состоит из
двух компонент: кинетической и потенциальной
энергий
mv 2 kx 2
Eполн Eк Eп
const
2
2
Так как при максимальном отклонении x = A
потенциальная энергия достигает своего максимума,
а кинетическая равна нулю (v = 0), то полная энергия
Eполн
kA2
2

16. ЗАТУХАЮЩИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

16
При малых скоростях Fтр r v
ma Fупр Fтр k x r v
Затухающие колебания описываются ОДУ:
mx r x k x 0 ,
x 2 x 02 x 0
k
где 0
собственная частота колебаний,
m
r
коэффициент затухания.
2m

17. РЕШЕНИЕ ДУ ЗАТУХАЮЩИХ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

2
x 2 x 0 x 0 ( 0 )
Характеристическое уравнение: 2 2 02 0
D b 2 4ac (2 )2 4 1 02 4 2 4 02 0
Его комплексные корни
4 4 0
b D
2
2
2
1,2
i 0 ,
2a
2 1
2 1
2
2
Имеем, a , b 02 2 , поэтому
x e t (C1 cos t C2 sin t ) A0e t sin ( t 0 )
17

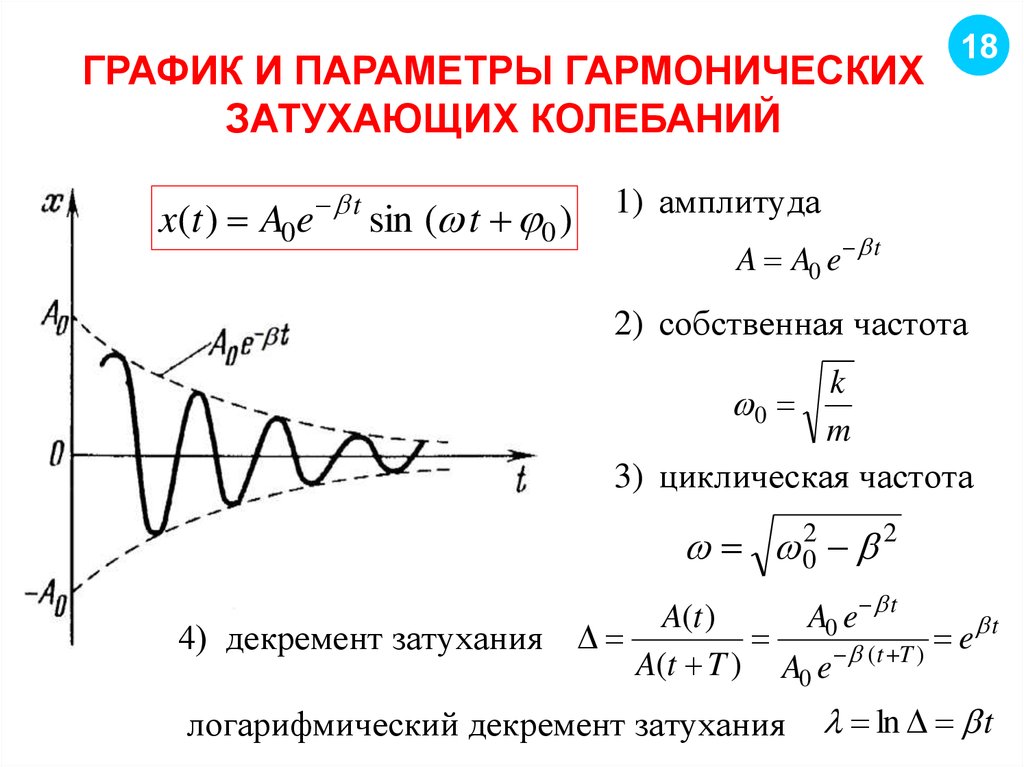
18. ГРАФИК И ПАРАМЕТРЫ ГАРМОНИЧЕСКИХ ЗАТУХАЮЩИХ КОЛЕБАНИЙ

x(t ) A0e t sin ( t 0 )
18
1) амплитуда
A A0 e t
2) собственная частота
k
m
3) циклическая частота
0
02 2
A(t )
A0 e t
t
e
4) декремент затухания
A(t T ) A0 e (t T )
логарифмический декремент затухания
ln t

19. ЭНЕРГИЯ ЗАТУХАЮЩИХ ГАРМОНИЧЕКИХ КОЛЕБАНИЙ

Полная энергия гармонических затухающих
колебаний
kA 2 k A02 e 2 t
Eполн Eк Eп
const
2
2
т.к. амплитуда уменьшается по закону A A0 e t
19

20. ЗАТУХАЮЩИЕ НЕГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

2
x 2 x 0 x 0
1) 0 ( D = 0 ):
один корень
x A0 e t
2) 0 ( D > 0 ):
два корня
1,2
x C1e 1t C2e 2t
D 4 2 4 02 0
20

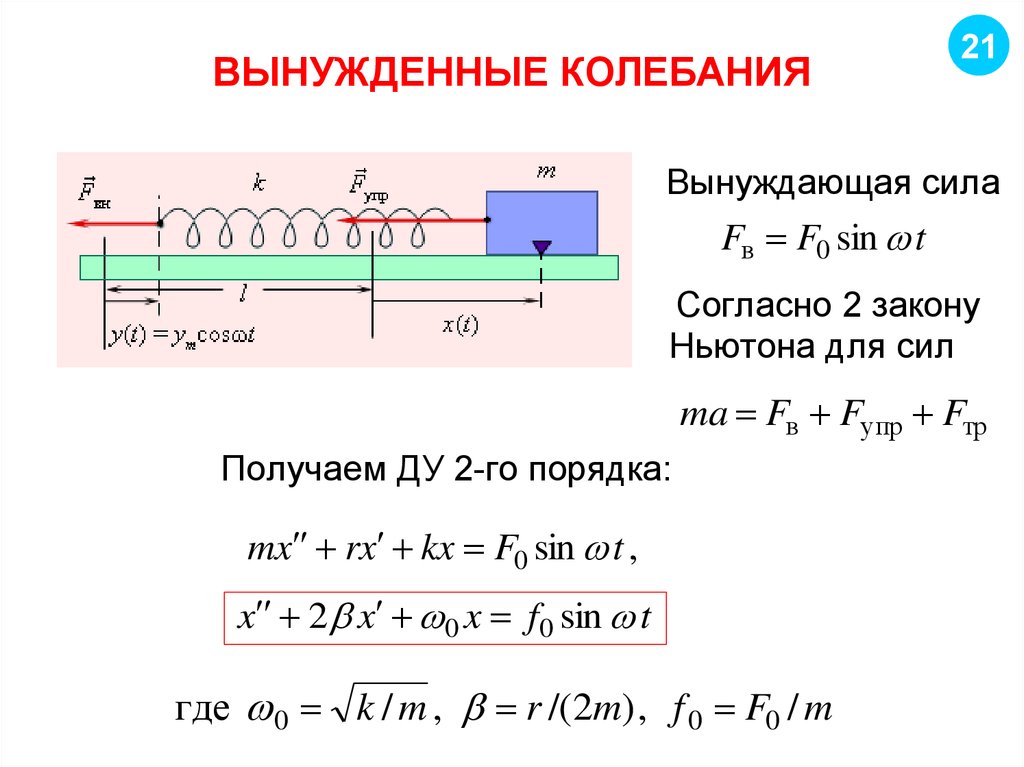
21. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

21
Вынуждающая сила
Fв F0 sin t
Согласно 2 закону
Ньютона для сил
ma Fв Fупр Fтр
Получаем ДУ 2-го порядка:
mx rx kx F0 sin t ,
x 2 x 0 x f 0 sin t
где 0 k / m , r /(2m) , f 0 F0 / m

22. РЕШЕНИЕ ДУ ВЫНУЖДЕННЫХ КОЛЕБАНИЙ

22
Решение ДУ вынужденных колебаний состоит
из двух слагаемых: одно из них соответствует
процессу установления колебаний со временем
(им можно пренебречь), второе - установившимся
колебаниям.
x Asin( t )
где
A
f0
( 02 2 ) 2 4 2 2
2
arctg 2
0 2

23. ЯВЛЕНИЕ РЕЗОНАНСА

23
ЯВЛЕНИЕ РЕЗОНАНСА
При некоторой частоте
рез амплитуда
колебаний A достигает
максимальное значение.
Это явление называется
резонансом.
Из необходимого условия
экстремума функции A' =
0
f 0 (2( 02 2 ) 2 8 2 )
4 f 0 ( 02 2 2 2 )
A
A
0
3
3
2 ( 02 2 ) 2 4 2 2
2 ( 02 2 ) 2 4 2 2
02 2 2 2 0 рез
02
2
2
Aрез
f0
2 02 2 2

24. ПРИМЕРЫ ПРОЯВЛЕНИЯ РЕЗОНАНСА

Полезный резонанс
Вредный резонанс
1. Настройка радио
1. Разрушение сооружений
2. Резонаторы в
музыкальных
инструментах
2. Вредное воздействие
низкочастотного звука
на работу сердца
3. Восприятие
звука ухом
человека
3. Повышенные
резонансные токи в
электрической цепи
24

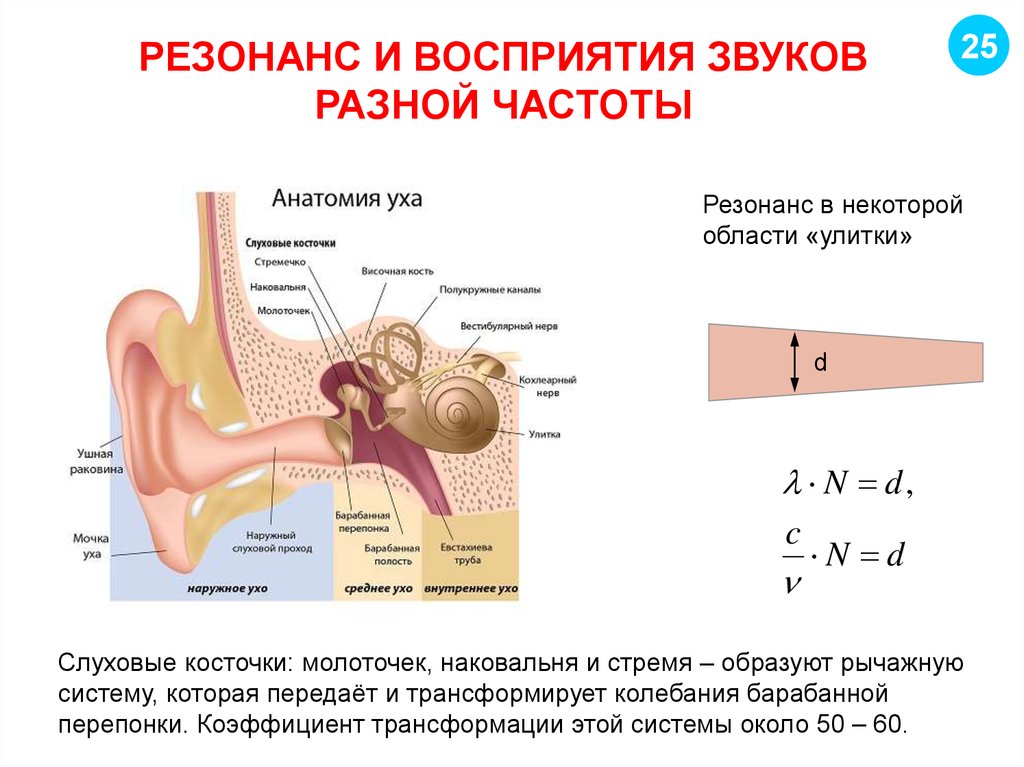
25. РЕЗОНАНС И ВОСПРИЯТИЯ ЗВУКОВ РАЗНОЙ ЧАСТОТЫ

25
Резонанс в некоторой
области «улитки»
d
N d,
c
N d
Слуховые косточки: молоточек, наковальня и стремя – образуют рычажную
систему, которая передаёт и трансформирует колебания барабанной
перепонки. Коэффициент трансформации этой системы около 50 – 60.

26. III. Звуковые волны

def Звук ‒ это механические колебания (волны)
небольшой частоты, распространяющиеся в
упругих средах (твердых телах, жидкостях и
газах).
В газах и жидкостях звук представляет собой
продольные волны, в твердых телах звуковые
колебания могут быть и поперечными.
Скорость звука меняется в зависимости от типа и
состояния среды. Как правило, в газах скорость
звука меньше, чем в жидкостях, а в жидкостях ‒
меньше, чем в твёрдых телах.
с vвоздух 330 м/с
26

27. ЧАСТОТЫ, ВОСПРИНИМАЕМЫЕ УХОМ ЧЕЛОВЕКА

27
ЧАСТОТЫ, ВОСПРИНИМАЕМЫЕ
УХОМ ЧЕЛОВЕКА
ИНФРАЗВУК
16 Гц
20 000 Гц
УЛЬТРАЗВУК
v, Гц
Порог слышимости ‒ минимальное звуковое давление
(или интенсивность звука), при котором звук данной частоты
воспринимается ухом человека.
Величину порога слышимости выражают в децибелах.
За нулевой уровень принято звуковое давление 2·10 -5 Па
(I0 = 10 -12 Вт/м 2) на частоте 1 кГц.

28. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЗВУКА

28
def Интенсивность звука ‒ это энергия звуковой
волны, падающая на единицу площади за
единицу времени.
I
W
St
[I ]
Дж Вт
2
2
м с м
W
Вектор Умова, I
v w v , показывает направление
V
распространения волны и равен количеству энергии,
переносимой за единицу времени через единицу площади
поверхности, перпендикулярной к распространению волны.
При v 1 кГц : I min I 0 10 12 Вт / м2 (порог слышимости)
I max 102 Вт / м2 (болевой порог)

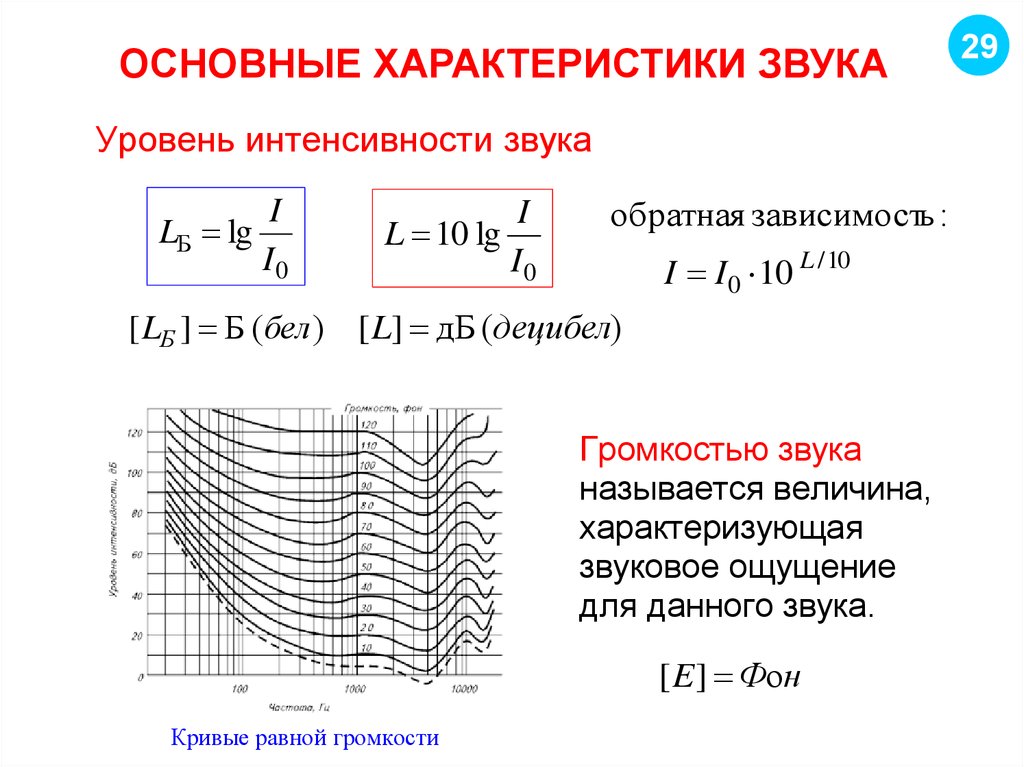
29. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЗВУКА

Уровень интенсивности звука
LБ lg
I
I0
I
L 10 lg
I0
обратная зависимость :
I I 0 10 L / 10
[ LБ ] Б (бел ) [ L] дБ (децибел)
Громкостью звука
называется величина,
характеризующая
звуковое ощущение
для данного звука.
[ E ] Фон
Кривые равной громкости
29

30. ЗАКОН ВЕБЕРА-ФЕХНЕРА

Увеличение раздражения (интенсивности) в
геометрической прогрессии вызывает увеличение
его ощущения (громкости) в арифметической
прогрессии
I
E k lg
I0
где коэффициент пропорциональности k сложным
образом зависит от частоты и интенсивности звука
(условно принимают, что на частоте 1 кГц k = 1).
30

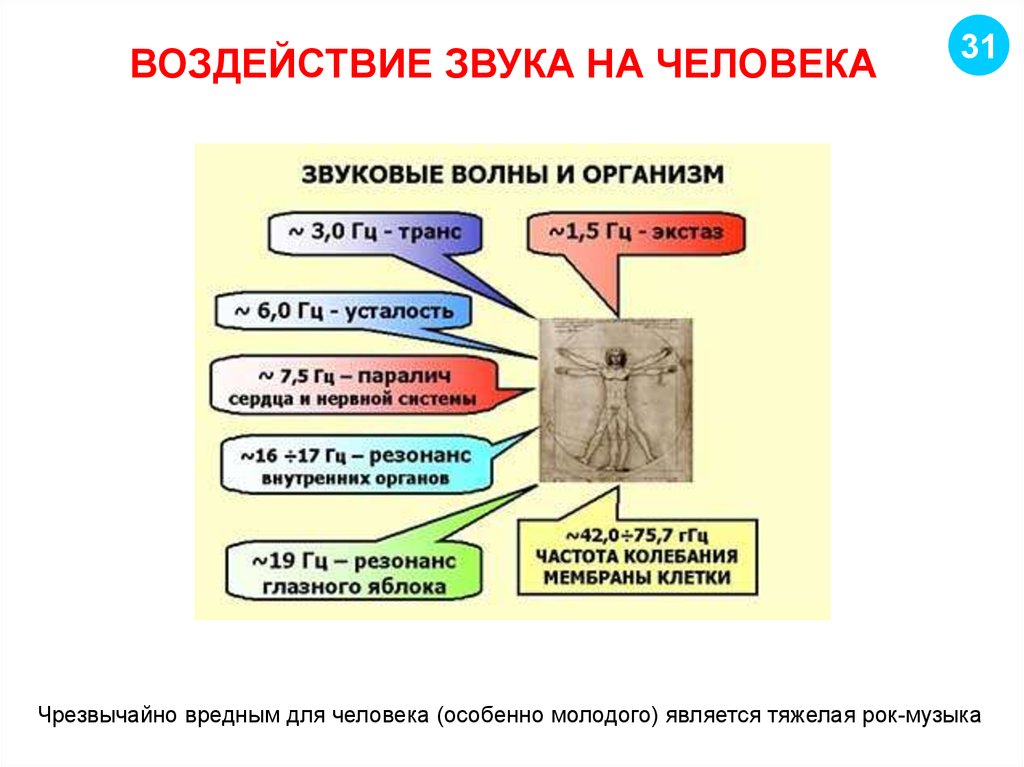
31. ВОЗДЕЙСТВИЕ ЗВУКА НА ЧЕЛОВЕКА

31
Чрезвычайно вредным для человека (особенно молодого) является тяжелая рок-музыка

32. ВОЗДЕЙСТВИЕ ЗВУКА НА ВОДУ

32

33. СПАСИБО ЗА ВНИМАНИЕ !