Векторы. Сложение векторов

1. Векторы

Напомним, что вектором называется направленный
отрезок, т.е. отрезок, в котором указаны его начало и
конец.
Вектор с началом в точке А и концом в точке В
обозначается AB и изображается стрелкой с началом в
точке А и концом в точке В.
Длиной, или модулем, вектора называется длина
соответствующего отрезка. Длина векторов AB ,
a обозначается соответственно | AB|, | a |.
Два вектора называются равными, если они имеют
одинаковую длину и направление.
Рассматривают также нулевые векторы, у которых начало
совпадает с концом. Все нулевые векторы считаются
равными между собой. Они обозначаются 0 , и их длина
считается равной нулю.

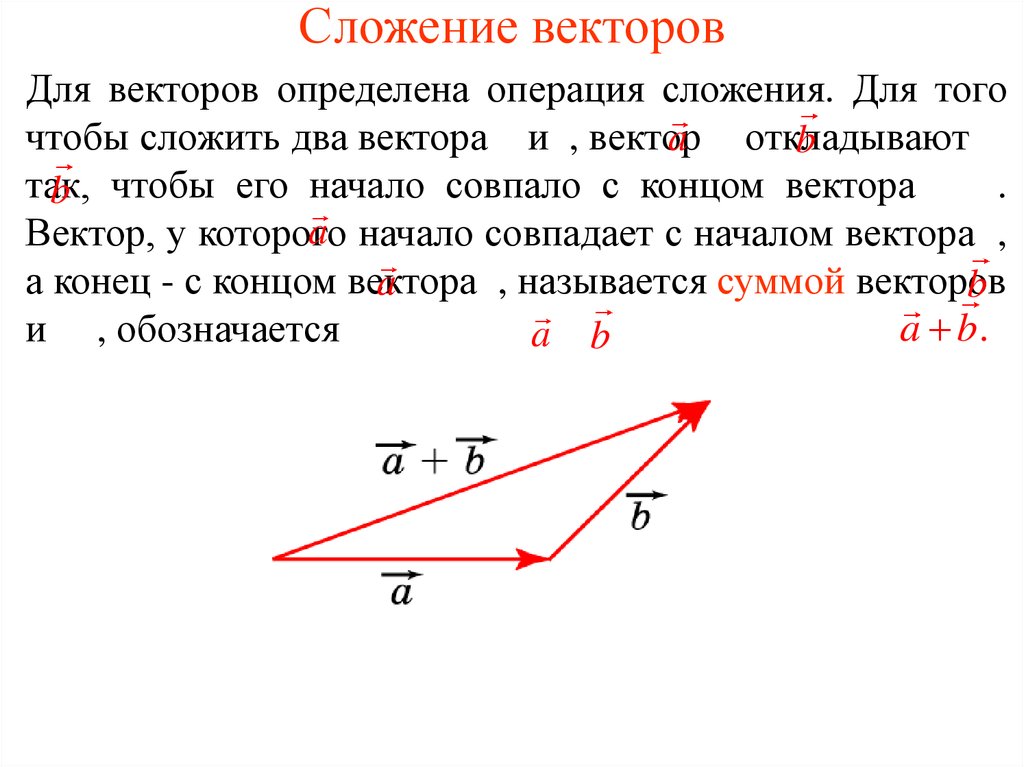
2. Сложение векторов

Для векторов определена операция сложения. Для того
чтобы сложить два вектора и , вектор
a откладывают
b
так,
.
b чтобы его начало совпало с концом вектора
a начало совпадает с началом вектора ,
Вектор, у которого
а конец - с концом вектора
, называется суммой векторов
a
b
a b.
и , обозначается
a b

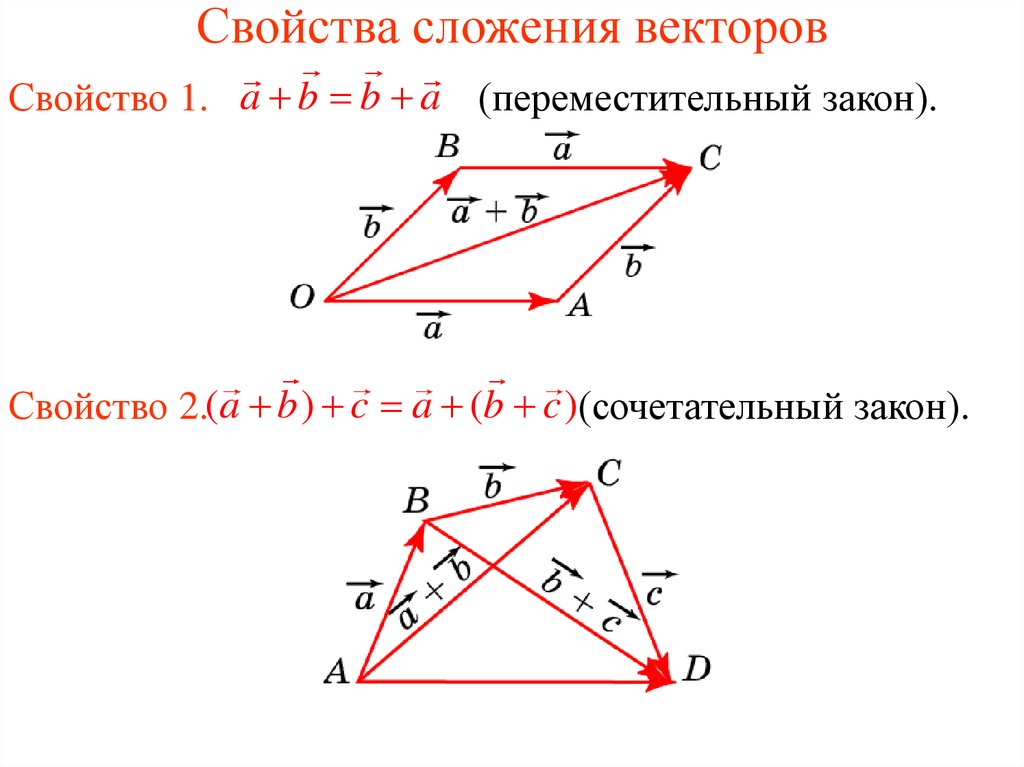
3. Свойства сложения векторов

Свойство 1. a b b a (переместительный закон).
Свойство 2.(a b ) c a (b c )(сочетательный закон).

4. Пример

Сколько различных векторов задают
вершин параллелограмма ABCD?
Ответ: Восемь векторов.
пары

5. Упражнение 1

Сколько различных векторов задают стороны
трапеции ABCD?
Ответ: Восемь векторов.

6. Упражнение 2

В прямоугольнике АВСD АВ = 3 см, ВС = 4 см.
Найдите длины векторов: а) AB ; б) BC ; в) DC ;
г) AC ; д) DB .
Ответ: а) 3 см;
б) 4 см;
в) 3 см;
г) 5 см;
д) 5 см.

7. Упражнение 3

Основание AD трапеции АВСD с прямым углом
А равно 12 см, АВ = 5 см, D = 45°. Найдите
длины векторов: а) BD ; б) CD ; в) AC .
Ответ: а) 13 см;
б) 5 2 см;
в) 74 см.

8. Упражнение 4

В
параллелограмме
АВСD
диагонали
пересекаются в точке О. Равны ли векторы: а)
AB и DC ; б) BC и DA ; в) AO и OC ; г) AC и BD ?
Ответ: а) Да;
б) нет;
в) да;
г) нет.

9. Упражнение 5

Точки S и T являются серединами боковых
сторон соответственно MN и LK равнобедренной
трапеции MNLK. Равны ли векторы: а) MS и SN ;
б) MN и KL ; в) TS и LM ; г) TL и KT ?
Ответ: а) Да;
б) нет;
в) нет.
г) да.

10. Упражнение 6

В треугольнике АВС укажите векторы:
а) AB BC ;
б) CB BA;
в) CA AB;
г) BA CB.
Ответ: а) AC ;
б) CA ;
в) CB ;
г) CA .

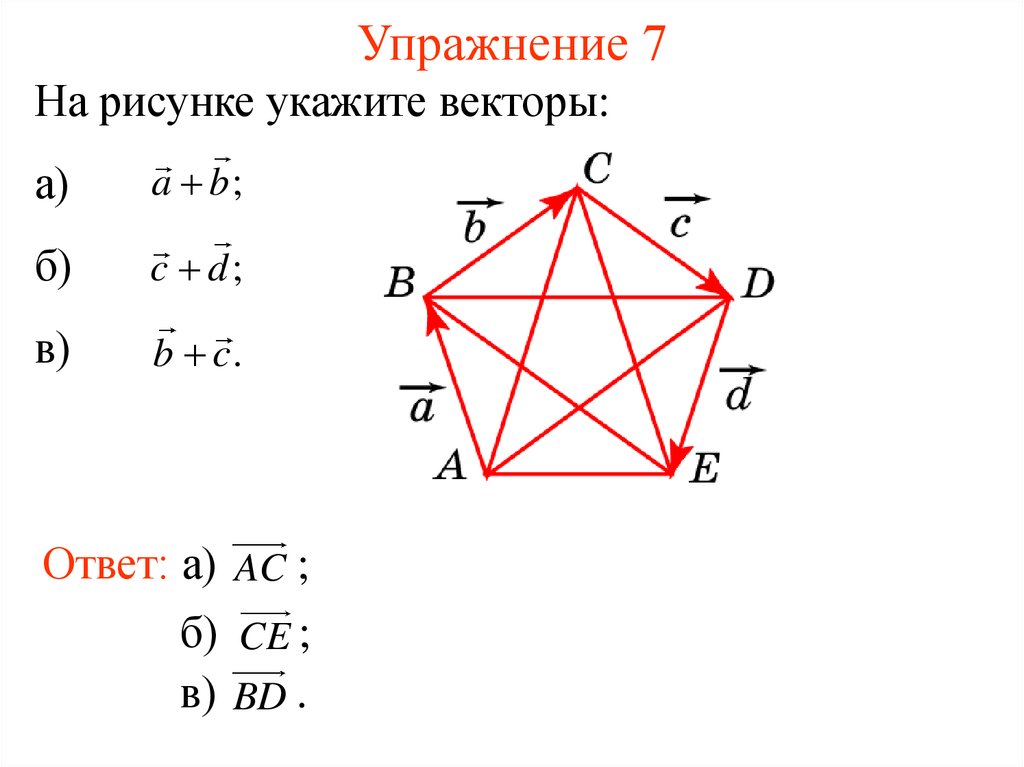
11. Упражнение 7

На рисунке укажите векторы:
а)
a b;
б)
c d;
в)
b c.
Ответ: а) AC ;
б) CE ;
в) BD .

12. Упражнение 8

А, В, С, D - произвольные точки плоскости.
Выразите через векторы a AB , b BC , c CD
векторы: а) AD ; б) BD ; в) AC .
Ответ: а) a b c ;
б) b c ;
в) a b .

13. Упражнение 9

Сторона равностороннего треугольника АВС
равна а. Найдите: а) | AB BC | ; б) | AB AC | ;
в) | AB CB | .
Ответ: а) a;
б) a 3 ;
в) a 3 .

14. Упражнение 10

В треугольнике АВС АВ = 6, ВС = 8, B = 90°.
Найдите: а) | AB | | BC | ; б) | AB BC | ; в) | BA | | BC |;
г) | BA BC | .
Ответ: а) 14;
б) 10;
в) 14;
г) 10.

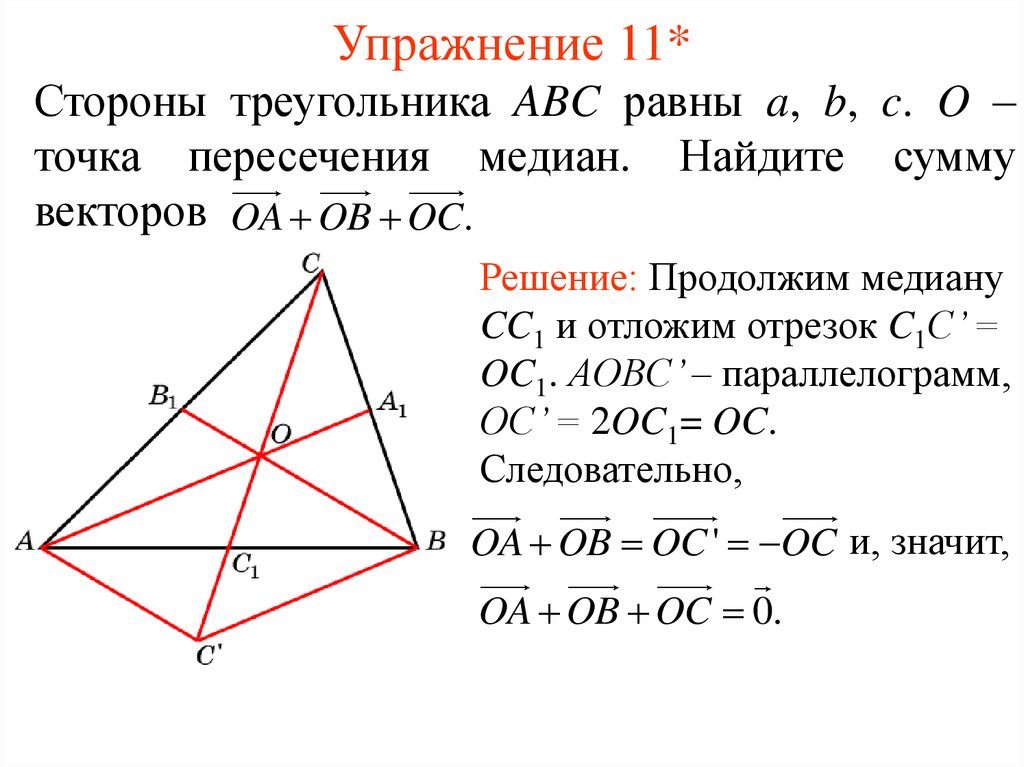
15. Упражнение 11*

Стороны треугольника ABC равны a, b, c. O –
точка пересечения медиан. Найдите сумму
векторов OA OB OC.
Решение: Продолжим медиану
CC1 и отложим отрезок C1C’ =
OC1. AOBC’ – параллелограмм,
OC’ = 2OC1= OC.
Следовательно,
OA OB OC ' OC и, значит,
OA OB OC 0.