Similar presentations:
Ланки систем автоматичного керування
1. Ланки систем автоматичного керування
1. Класифікація ланок САК2. Мінімально-фазові ланки
1. Позиційні
2. Інтегруючі
3. Диференціюючі
3. Немінімально-фазові ланки
2. Класифікація ланок САК
Процеси в різних за соїми фізичнимиприципами дії та конструкцією
елементів систем автоматичного
керування можуть визначатися
подібними диференційними рівняннями
динаміки.
3. Класифікація ланок САК
Рівняння динаміки для механічної системиз масою m та коефіцієнтом опору k
dv
m
kv F
dt
Рівняння динаміки активно-індуктивного
кола з активним опором R та
індуктивністю L
di
L
Ri u
dt
4. Класифікація ланок САК
Динамічна ланка – це пристрій,робота якого описується певним
диференційним рівнянням.
Конструктивне виконання і
фізичний процес, на якому
базується робота пристрою, не
мають значення при визначенні
типу ланки
5. Класифікація ланок САК
З лівої частини рівняння динаміки ланки, вякій представлені вихідна величина та її
похідні, видно, як швидко та точно реагує
ланка на вхідну величину
Якщо похідних у лівій частині рівняння
динаміки ланки немає, то це означає, що
елемент миттєво реагує на вхідну
величину
6. Класифікація ланок САК
Права частини рівняння динаміки ланкипоказує, на що вона реагує і з яким
коефіцієнтом передачі вхідна величина
з’являється на виході
Залежно від вигляду правої частини ланка
може реагувати
на саму вхідну величину
тільки на похідну від вхідної величини
тільки на інтеграл від вхідної величини
на вхідну величину і її похідну
на вхідну величину та інтеграл від неї
7. Класифікація ланок САК
Рівняння динаміки однозначно визначаютьпередаточну функцію ланки
Особливостями передаточної функції є
нулі передаточної функції
полюси передаточної функції
Передаточна функція записується у вигляді
k1 N p
W p
L p
Нулі передаточної функції – це корені рівняння
N p 0
Полюси передатоіної функції – це корені рівняння
L p 0
8. Класифікація ланок САК
Будь-яку систему автоматичногокерування можна представити у вигляді
з’єднання типових динамічних ланок
Типовою називається динамічна ланка,
яка описується диференційним рівнянням
не вище другого порядку
9. Класифікація ланок САК
Динамічніланки
Позиційні
Мінімальнофазові
Немінімальнофазові
Інтеруючі
Диференціюючі
10. Класифікація ланок САК
Мінімально-фазовою називається ланка,нулі та полюси якої від’ємні або мають
від’ємні дійсні частини
Немінімально-фазовою називається
ланка, у якої хоча б один нуль або полюс
додатний або має додатну дійсну частину
Назва ланок зумовлена зсувом фаз
фазочастотної характеристики. У
мінімально-фазових зсув фаз мінімально
можливий для даного порядку рівняння
динаміки
11. Класифікація ланок САК
Позиційною називається ланка, у якої вусталеному режимі вихідна величина
прямо пропорційна вхідній
x
x k1g
0
g
12. Класифікація ланок САК
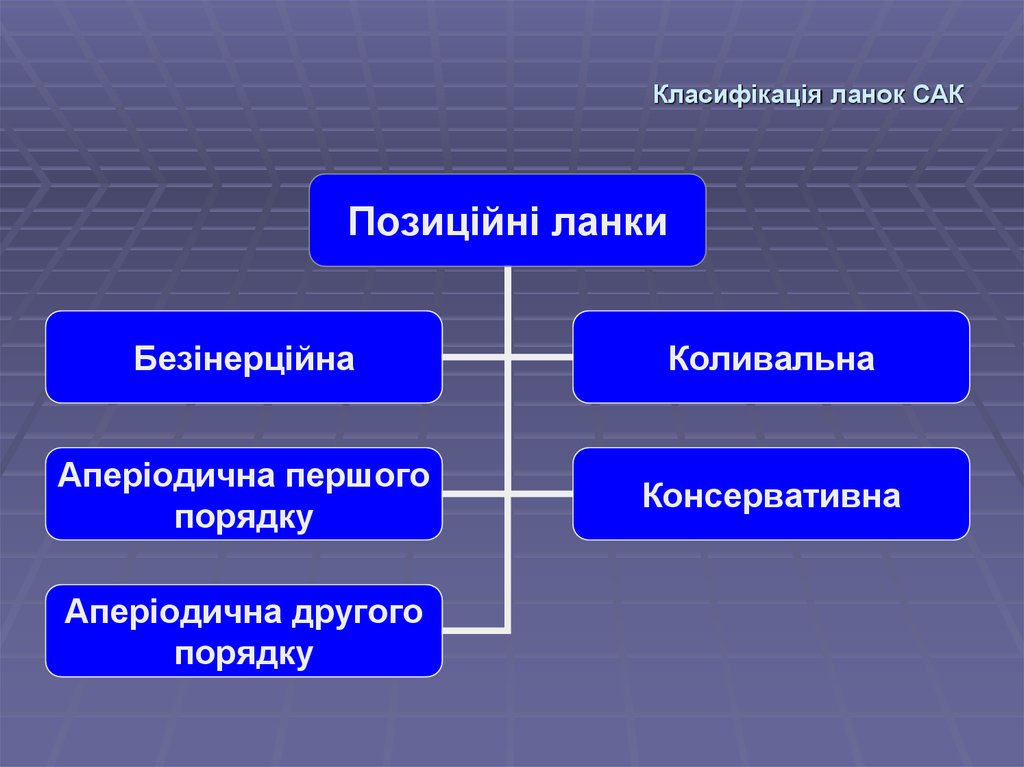
Позиційні ланкиБезінерційна
Коливальна
Аперіодична першого
порядку
Консервативна
Аперіодична другого
порядку
13. Класифікація ланок САК
Інтегруючою називається ланка, у якої вусталеному режимі швидкість зміни
вихідої величини прямо пропорційна
вхідній
dx
dt
dx
k1g
dt
0
g
14. Класифікація ланок САК
Для інтегруючої ланки в усталеномурежимі буде справедлива залежність
x k1 g dt
Звідси й походить назва ланки –
інтегруюча
15. Класифікація ланок САК
Інтегруючіланки
Ідеальна
інтегруюча
Реальна
інтегруюча
Ізодромна
16. Класифікація ланок САК
диференціюючою називається ланка, уякої в усталеному режимі вихіда величина
прямо пропорційна швидкості зміни
вхідної
x
dg
x k1
dt
0
dg
dt
17. Класифікація ланок САК
Диференціюючіланки
Ідеальна
диференціююча
Реальна
диференціююча
Ідеальна з
введенням похідної
18. Позиційні ланки Безінерційна ланка
1. Рівняння динамікиx t k1 g t
2. Рівняння динаміки в операторному вигляді
x k1 g
3. Передаточна функція
W p k1
4. Частотна передаточна функція
W j k1
19. Позиційні ланки Безінерційна ланка
5. Часові характеристики5.1 Перехідна функція
h t k1 1 t
k1
h(t)
5.2 Вагова функція
w t k1 t
w(t)
h( t )
0
t
t
0
t
20. Позиційні ланки Безінерційна ланка
6. Частотні характеристики6.1 Амплітудно-частотна
A k1
6.2 Фазо-частотна
0
φ(ω)
A(ω)
k1
0
ω
0
ω
21. Позиційні ланки Безінерційна ланка
6. Частотні характеристики6.3 Амплітудно-фазова
A k 1
V
0 k1 U
6.4 Логарифмічні
амплітудна і фазова
20lgk1
0
Lm(ω)
φ(ω)
0
ω
22. Позиційні ланки Безінерційна ланка
6. Частотні характеристики6.5 Дійсна
U k1
6.6 Уявна
V 0
V(ω)
U(ω)
k1
0
ω
0
ω
23. Позиційні ланки Аперіодична першого порядку
1. Рівняння динамікиT1x t x t k1 g t
2. Рівняння динаміки в операторному вигляді
T1p 1 x k1 g
3. Передаточна функція
k1
W p
T1p 1
4. Частотна передаточна функція
k1
W j
1 jT1
24. Позиційні ланки Аперіодична першого порядку
5. Часові характеристики5.1 Перехідна функція
t
h t k1 1 e T1
k1
5.2 Вагова функція
k1
w t e
T1
t
T1
w(t)
h(t)
w1( t )
)
T1
0
t
0 T1
t
25. Позиційні ланки Аперіодична першого порядку
6. Частотні характеристики6.1 Амплітудно-частотна
A
6.2 Фазо-частотна
k1
T1
2
arctgT1
1
φ(ω)
A(ω)
1( )
A 1( )
0
ω
0
ω
26. Позиційні ланки Аперіодична першого порядку
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
20
90
10
45
0
0
Lm1( )
V1( )
Lm2( )
10
20
0.1
U1( )
45
1
10
90
100
1( )
27. Позиційні ланки Аперіодична першого порядку
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
5
0
4
1
3
U 1( )
V1( )
2
2
1
0
3
0
20
40
60
80
100
0
20
40
60
80
100
28. Позиційні ланки Аперіодична другого порядку
1. Рівняння динамікиt T1x t x t k1 g t
T22x
Для аперіодичної ланки другого порядку
повинна виконуватись умова
T1 2T2
2. Рівняння динаміки в операторному вигляді
T p
2
2
2
T1p 1 x k1g
29. Позиційні ланки Аперіодична другого порядку
Введемо позначенняT1
T3
2
T12
T22
4
T1
T12
T4
T22
2
4
3. Передаточна функція
k1
W p
T3p 1 T4p 1
4. Частотна передаточна функція
k1
W j
1 jT3 1 jT4
30. Позиційні ланки Аперіодична другого порядку
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
t
t
t
t
k
T
T
T
T
T
T
1
3
4
3
4
3
4
e e
h t k1 1
e
e w t
T
T
T
T
T
T
3
4
3
4
3
4
6
10
5
8
4
h( t )
6
3
w( t )
2
4
1
2
0
0
0.5
1
t
1.5
2
0
0
0.5
1
t
1.5
2
31. Позиційні ланки Аперіодична другого порядку
6. Частотні характеристики6.1 Амплітудно-частотна
k1
A
T3 2 1 T4 2 1
5
6.2 Фазо-частотна
arctgT3 arctgT 4
0
4
45
3
A 1( )
1( ) 90
2
135
1
0
0
20
40
60
80
100
180
0
20
40
60
80
100
32. Позиційні ланки Аперіодична другого порядку
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
0
1
Lm1( )
V1( )
90
0
0
1( )
Lm2( )
20
2
3
2
20
0
2
U 1( )
4
6
40
0.1
90
1
10
180
100
33. Позиційні ланки Аперіодична другого порядку
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
6
0
4
1
V1( )
U 1( ) 2
2
0
2
3
0
20
40
60
80
100
0
20
40
60
80
100
34. Позиційні ланки Коливальна
1. Рівняння динамікиt T1x t x t k1 g t
T22x
Для коливальної ланки повинна
виконуватись умова
T1 2T2
2. Рівняння динаміки в операторному вигляді
T p
2
2
2
T1p 1 x k1g
35. Позиційні ланки Коливальна
Введемо позначенняT1
2 T2
Тоді рівняння динаміки
t 2 T2 x t x t k1 g t
T22 x
T p
2
2
2
2 T2 p 1 x k1g
3. Передаточна функція
W p
k1
T22p2 2 T2p 1
4. Частотна передаточна функція
k1
W j 2
2
T2 j 2 j T2 1
36. Позиційні ланки Коливальна
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
1 2
1 2
T2
h t k1 1 e t cos
t
sin
2
T
T2
1
2
t
w t
10
e
t
T3
1 2
sin
t
T2
1
5
w( t )
2.5
0
T2 1 2
2
7.5
h( t )
k1
0
1
0
2
4
6
t
8
10
2
0
2
4
6
t
8
10
37. Позиційні ланки Коливальна
5. Часові характеристики5.3 Вплив коефіцієнта
демпфірування на
перехідну функцію
5.4 Вплив сталої часу
на перехідну функція
10
h1( t 0.1)
h1( t 0.2)
10
7.5
h2( t 0.2)
h2( t 0.4)
5
h1( t 0.7)
7.5
5
h2( t 1)
2.5
0
2.5
0
2
4
6
t
8
10
0
0
2
4
6
t
8
10
38. Позиційні ланки Коливальна
6. Частотні характеристики6.1 Амплітудно-частотна
k1
A
1 T 2 T
2
2
2 2
2
2
6.2 Фазо-частотна
2 T2
arctg
1 T22 2
2
2 T2
arctg T 2 2 1
2
30
0
45
20
1( ) 90
A 1( )
10
135
180
0
0
20
40
60
80
100
0
20
40
60
80
100
39. Позиційні ланки Коливальна
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
40
0
90
20
10
Lm1( )
V1( )
0
0
1( )
Lm2( )
20
20
90
40
30
20
10
0
U 1( )
10
20
60
0.01
0.1
1
10
180
100
40. Позиційні ланки Коливальна
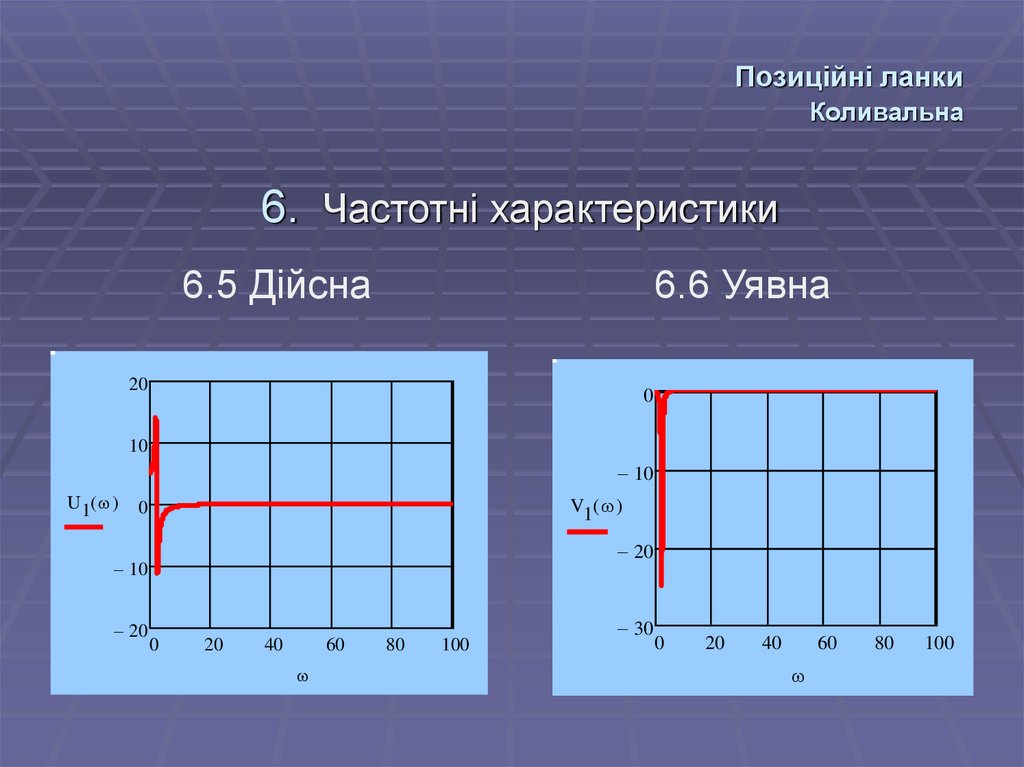
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
20
0
10
10
U 1( )
V1( )
0
20
10
20
0
20
40
60
80
100
30
0
20
40
60
80
100
41. Позиційні ланки Коливальна
6. Частотні характеристикиВплив коефіцієнта демпфірування на частотні
характеристики
6.8 Логарифмічні
6.7 АФЧХ
0
40
10
V2( 0.05)
20
V2( 0.2)
V2( 0.7)
Lm3( 0.05) 20
90
Lm3( 0.2)
0
30
Lm3( 0.7)
40
Lm2( )
50
40
20
0
20
U2( 0.05) U2( 0.2) U2( 0.7)
40
180
2( 0.05)
0
2( 0.2)
20
90 ( 0.7)
2
40
180
60
0.01
0.1
1
10
270
100
42. Позиційні ланки Консервативна
1. Рівняння динамікиt x t k1 g t
Tx
2. Рівняння динаміки в операторному вигляді
2
1
T p
2
1
2
1 x k1g
3. Передаточна функція
W p
k1
T12p2 1
4. Частотна передаточна функція
k1
W j 2
2
T1 j 1
43. Позиційні ланки Консервативна
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
t
h t k1 1 cos
T1
h( t )
w t
10
25
5
12.5
0
w( t )
5
10
k1
t
sin
T1
T1
0
12.5
0
2
4
6
t
8
10
25
0
2
4
6
t
8
10
44. Позиційні ланки Консервативна
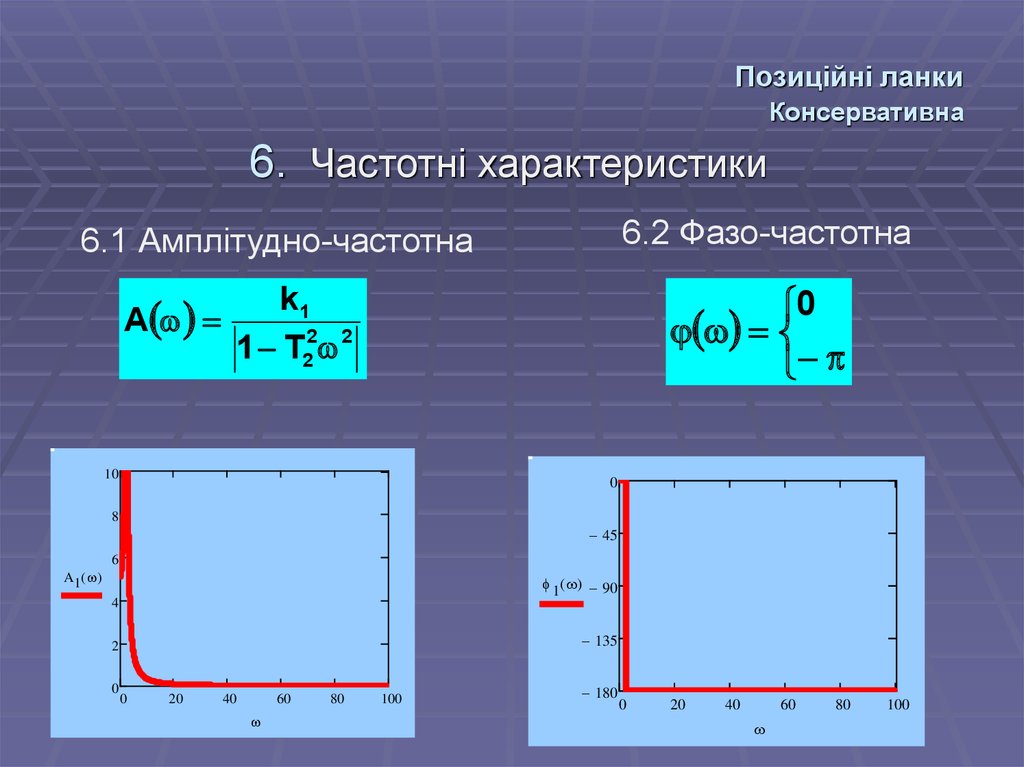
6. Частотні характеристики6.2 Фазо-частотна
6.1 Амплітудно-частотна
0
k1
A
1 T22 2
10
0
8
45
6
A 1( )
1( ) 90
4
135
2
0
0
20
40
60
80
100
180
0
20
40
60
80
100
45. Позиційні ланки Консервативна
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
1
180
0.5
V1( )
50
90
0
0
Lm1( )
0
Lm2( )
0.5
1
50
20
10
0
U 1( )
10
20
100
0.01
1( )
90
0.1
1
10
180
100
46. Позиційні ланки Консервативна
6. Частотні характеристики6.5 Дійсна
U 1( )
6.6 Уявна
10
1
5
0.5
V1( )
0
0
5
0.5
10
1
0
20
40
60
80
100
0
20
40
60
80
100
47. Інтегруючі ланки Ідеальна інтегруюча
1. Рівняння динамікиx t k1 g t
2. Рівняння динаміки в операторному вигляді
px k1g
3. Передаточна функція
W p
k1
p
4. Частотна передаточна функція
W j
k1
j
48. Інтегруючі ланки Ідеальна інтегруюча
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
h t k1t
h( t )
w t k 1
50
10
37.5
7.5
25
w( t )
12.5
0
5
2.5
0
2
4
6
t
8
10
0
0
2
4
6
t
8
10
49. Інтегруючі ланки Ідеальна інтегруюча
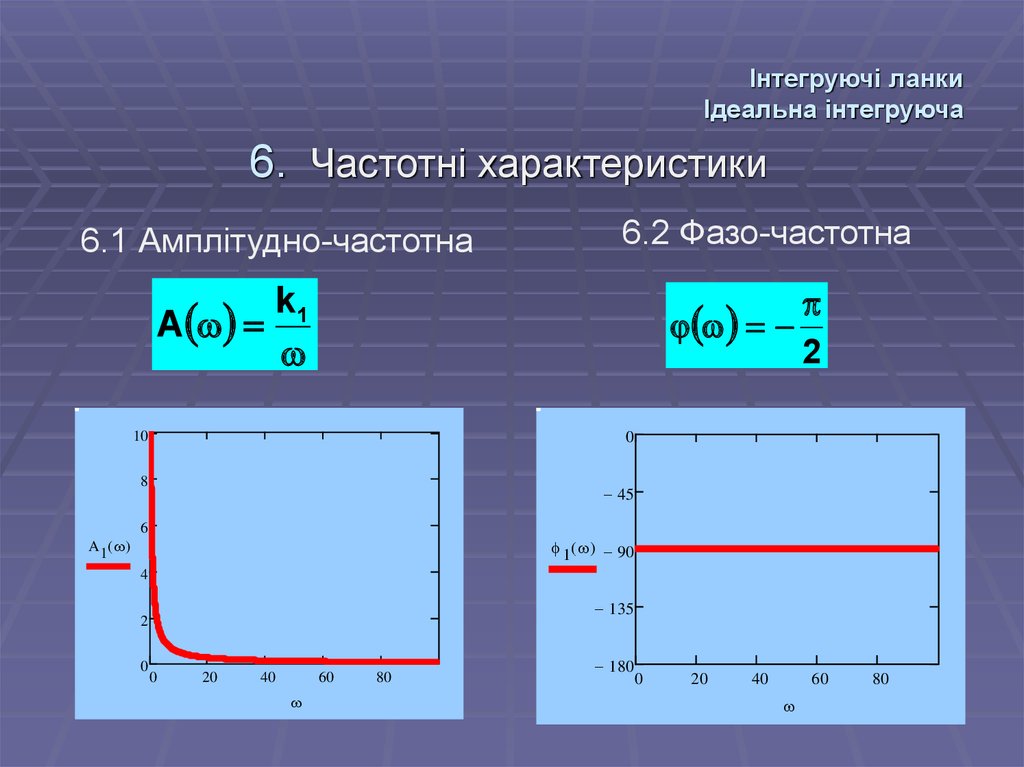
6. Частотні характеристики6.1 Амплітудно-частотна
6.2 Фазо-частотна
2
k1
A
10
0
8
45
6
A 1( )
1( ) 90
4
135
2
0
0
20
40
60
80
180
0
20
40
60
80
50. Інтегруючі ланки Ідеальна інтегруюча
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
0
60
270
100
40
180
20
90
200
V1( )
Lm1( )
1( )
300
0
400
20
500
20
10
0
U 1( )
10
20
40
0.01
0
90
0.1
1
10
180
100
51. Інтегруючі ланки Ідеальна інтегруюча
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
10
0
2
5
U 1( )
V1( )
0
5
10
4
6
8
0
20
40
60
80
10
0
20
40
60
80
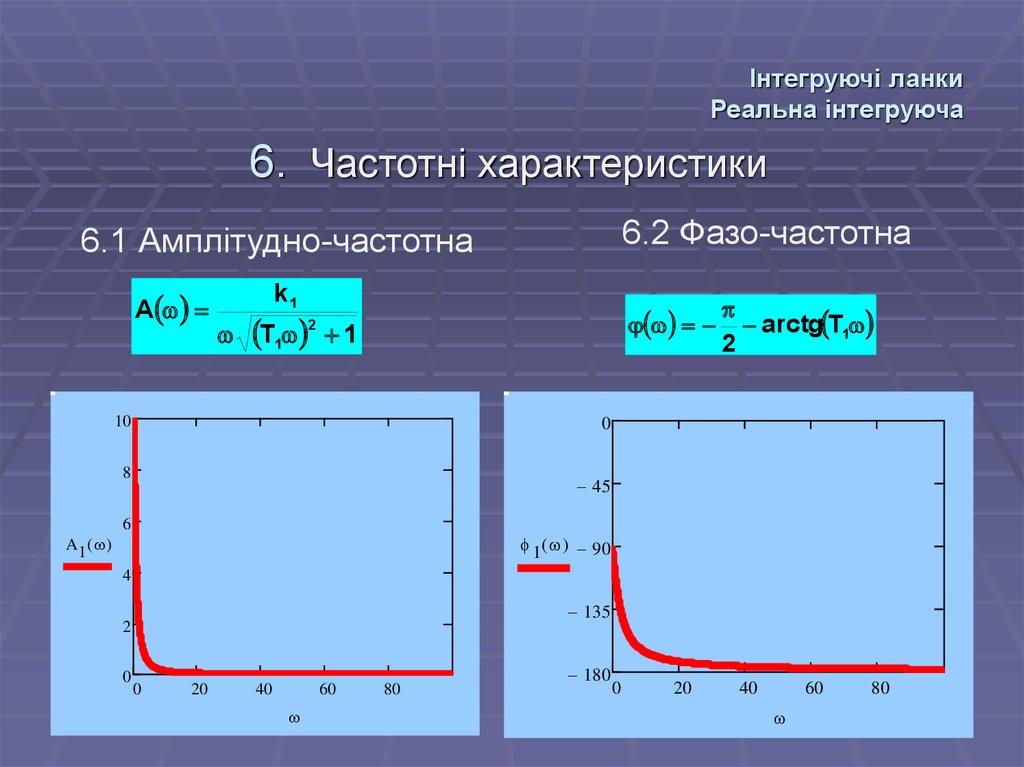
52. Інтегруючі ланки Реальна інтегруюча
1. Рівняння динамікиt x t k1 g t
T1x
2. Рівняння динаміки в операторному вигляді
p T1p 1 x k1g
3. Передаточна функція
k1
W p
p T1p 1
4. Частотна передаточна функція
k1
W j
j jT1 1
53. Інтегруючі ланки Реальна інтегруюча
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
t
T1
h t k1 t T1 1 e
20
10
15
7.5
h( t )
h2( t )
t
T1
w t k 1 1 e
w( t )
10
w 2( t )
5
0
5
2.5
0
1
2
t
3
4
0
0
1
2
t
3
4
54. Інтегруючі ланки Реальна інтегруюча
6. Частотні характеристики6.2 Фазо-частотна
6.1 Амплітудно-частотна
A
k1
T1 1
2
10
0
8
45
6
arctg T1
2
1( ) 90
A 1( )
4
135
2
0
0
20
40
60
80
180
0
20
40
60
80
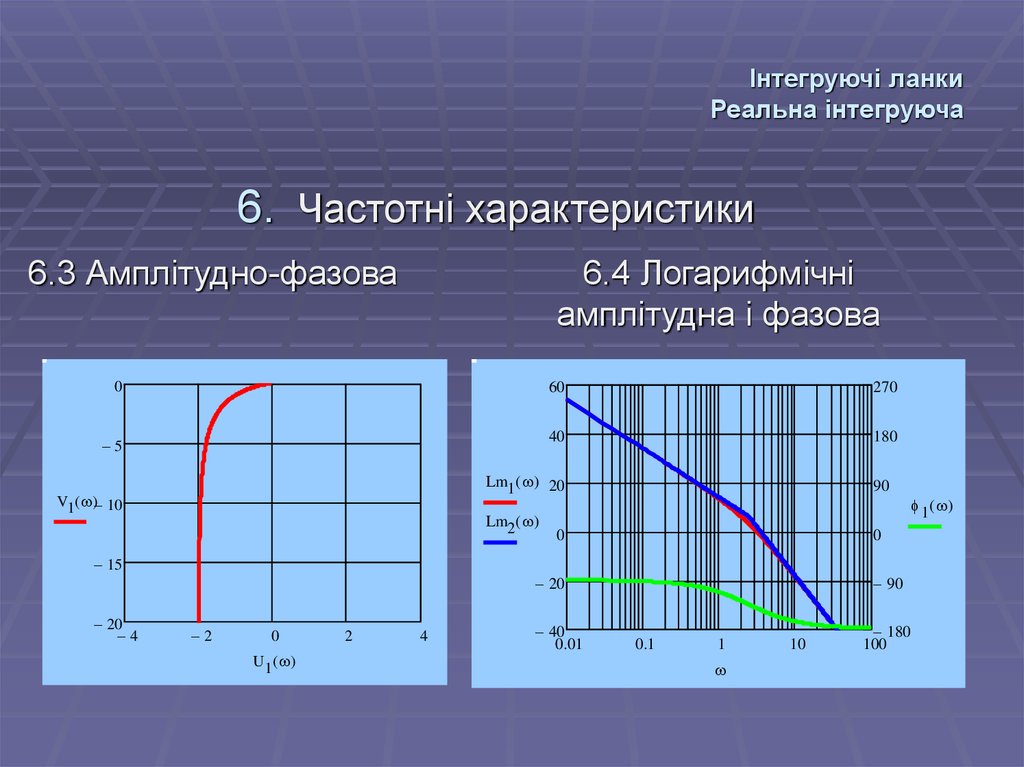
55. Інтегруючі ланки Реальна інтегруюча
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
0
60
270
5
40
180
V1( ) 10
Lm1( ) 20
90
Lm2( )
0
1( )
0
15
20
20
4
2
0
U 1( )
2
4
40
0.01
90
0.1
1
10
180
100
56. Інтегруючі ланки Реальна інтегруюча
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
0
0
2
1
V1( )
U1( ) 2
3
4
4
6
8
10
0
20
40
60
80
0
20
40
60
80
57. Інтегруючі ланки Ізодромна
1. Рівняння динамікиx t k 2g t k1g t
або
x t k 1 T1g t g t
де
k2
T1
k1
2. Рівняння динаміки в операторному вигляді
px k 2 p k 1 g
px k 1 T 1p 1 g
58. Інтегруючі ланки Ізодромна
3. Передаточна функціяk1
W p k 2
p
W p
k 1 T1p 1
p
4. Частотна передаточна функція
W j k 2
W j
k1
j
k 1 jT1 1
j
59. Інтегруючі ланки Ізодромна
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
h t k1 T1 t
w t k 1 T1 t 1
20
10
15
7.5
h( t ) 10
w( t )
2.5
5
0
5
0
0
1
2
t
3
4
0
1
2
t
3
4
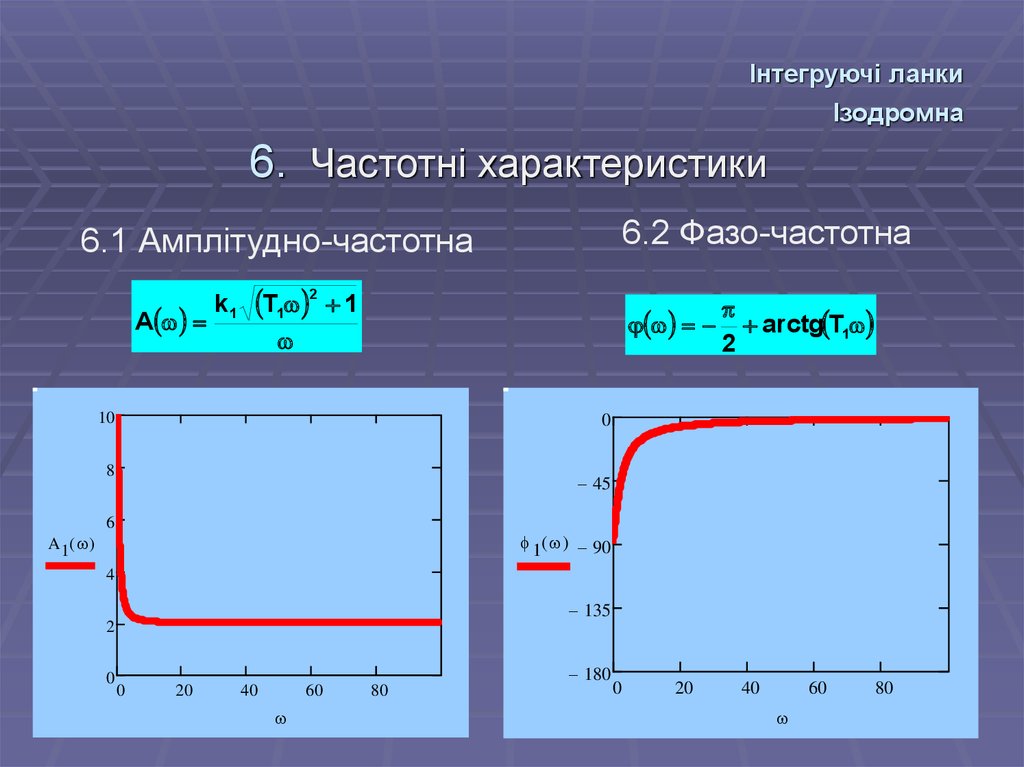
60. Інтегруючі ланки Ізодромна
6. Частотні характеристики6.2 Фазо-частотна
6.1 Амплітудно-частотна
A
k1
T1 2 1
10
0
8
45
6
arctg T1
2
1( ) 90
A 1( )
4
135
2
0
180
0
20
40
60
80
0
20
40
60
80
61. Інтегруючі ланки Ізодромна
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
0
5
V1( ) 10
60
270
40
180
Lm1( ) 20
90
Lm2( )
0
0
20
15
40
0.01
20
4
1( )
2
90
0.1
1
0
U 1( )
2
4
U1( 1) 2
10
180
100
62. Інтегруючі ланки Ізодромна
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
4
0
2
2
V1( )
U 1( ) 0
2
4
4
6
8
0
20
40
60
80
10
0
20
40
60
80
63. Диференціюючі ланки Ідеальна диференціююча
1. Рівняння динамікиx t T1g t
2. Рівняння динаміки в операторному вигляді
x T1pg
3. Передаточна функція
W p T1p
4. Частотна передаточна функція
W j jT1
64. Диференціюючі ланки Ідеальна диференціююча
5. Часові характеристики5.1 Перехідна функція
d t
w t T1
dt
T t k1 t
h(t)
0
5.2 Вагова функція
w(t)
t
0
t
65. Диференціюючі ланки Ідеальна диференціююча
6. Частотні характеристики6.1 Амплітудно-частотна
6.2 Фазо-частотна
A T1
40
180
30
135
A 1( )20
1( ) 90
10
45
0
0
20
40
60
80
0
0
20
40
2
60
80
66. Диференціюючі ланки Ідеальна диференціююча
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
20
10
V1( )
60
270
40
180
20
90
Lm1( )
0
1( )
0
10
20
4
0
20
2
0
U 1( )
2
4
40
0.01
90
0.1
1
10
180
100
67. Диференціюючі ланки Ідеальна диференціююча
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
40
4
2
20
V1( )
U 1( ) 0
0
2
4
0
20
40
60
80
20
0
20
40
60
80
68. Диференціюючі ланки Реальна диференціююча
1. Рівняння динамікиT2 x t x t T1g t
2. Рівняння динаміки в операторному вигляді
T2p 1 x T1pg
3. Передаточна функція
T1p
W p
T2p 1
4. Частотна передаточна функція
jT1
W j
jT2 1
69. Диференціюючі ланки Реальна диференціююча
5. Часові характеристики5.1 Перехідна функція
t
5.2 Вагова функція
t
T1
1 T2
w t
t e
T2
T2
T1 T2
h t
e
T2
5
1
4
0
1
3
w ( t ) 2
h( t )
2
3
1
0
4
0
0.5
1
t
1.5
2
5
0
0.5
1
t
1.5
2
70. Диференціюючі ланки Реальна диференціююча
6. Частотні характеристики6.1 Амплітудно-частотна
A
T1
6.2 Фазо-частотна
arctg T2
2
T2 2 1
5
180
4
135
3
1( ) 90
A 1( )
2
45
1
0
0
0
20
40
60
80
0
20
40
60
80
71. Диференціюючі ланки Реальна диференціююча
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
4
60
270
40
180
2
V1( ) 0
2
4
4
Lm1( ) 20
90
Lm2( )
0
1( )
0
20
2
0
U 1( )
2
4
40
0.01
90
0.1
1
10
180
100
72. Диференціюючі ланки Реальна диференціююча
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
40
4
2
20
V1( )
U 1( ) 0
0
2
4
0
20
40
60
80
20
0
20
40
60
80
73. Диференціюючі ланки Ідеальна з введенням похідної
1. Рівняння динамікиx t k1 T1g t g t
2. Рівняння динаміки в операторному вигляді
x k1 T1p 1 g
3. Передаточна функція
W p k1 T1p 1
4. Частотна передаточна функція
W j k1 jT1 1
74. Диференціюючі ланки Ідеальна з введенням похідної
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
h t k1 1 T1 t
d t
w t k1 t T1
d t
10
10
6.667
7.5
3.333
h( t )
w( t )
5
0
3.333
2.5
0
6.667
10
0
0.5
1
t
1.5
2
0
0.5
1
t
1.5
2
75. Диференціюючі ланки Ідеальна з введенням похідної
6. Частотні характеристики6.1 Амплітудно-частотна
A k1 T1 1
2
6.2 Фазо-частотна
arctg T1
20
180
15
135
A 1( )10
1( ) 90
45
5
0
0
0
2
4
6
8
0
20
40
60
80
76. Диференціюючі ланки Ідеальна з введенням похідної
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
100
80
60
270
40
180
60
Lm1( ) 20
90
40
Lm2( )
0
V1( )
20
0
1( )
0
20
0
2.5
5
U 1( )
7.5
10
40
0.01
90
0.1
1
10
180
100
77. Диференціюючі ланки Ідеальна з введенням похідної
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
10
200
7.5
150
U 1( ) 5
V1( )100
2.5
50
0
0
20
40
60
80
0
0
20
40
60
80
78. Немінімальнофазові ланки
Розглянуті відносяться до мінімально-фазових, а позиційні ланки – до стійких, або
ланок з самовирівнюванням
Самовирівнювання – це властивість ланки
самостійно приходити до нового усталеного
значення вихідного сигналу при обмеженій
зміні вхідного сигналу чи сигналу збурення
У деяких ланок обмежена зміна вхідного
сигналу чи сигналу збурення не означає
перехід ланки до нового усталеного стану, а
вихідна величина має тенденцію
необмеженого зростання з плином часу
79. Немінімальнофазові ланки
До таких ланок відносяться інтегруючі ланкиІснують ланки, у яких цей процес виражений більш
помітно
Це пояснюється наявністю додатніх дійсних коренів
або комплексних коренів з додатною дійсною
частиною в характеристичному рівняння. Та ланка
відноситья до категорії нестійких
Нестійкі ланки відносяться до немінімально-фазових,
оскільки мінімальні (за абсолютним значенням різниці
фаз будуть у стійких ланок)
До немінімально-фазових відносяться також стійкі
ланки, які маютьв чиельнику передаточної функції
додатні дійсні корені або комплексні корені з
додатною дійсною частиною
80. Немінімально-фазові ланки Квазіаперіодична першого порядку
1. Рівняння динамікиT1x t x t k1 g t
2. Рівняння динаміки в операторному вигляді
T1p 1 x k1 g
3. Передаточна функція
k1
W p
T1p 1
4. Частотна передаточна функція
k1
W j
1 jT1
81. Немінімально-фазові ланки Квазіаперіодична першого порядку
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
Tt
1
h t k1 e 1
k1
w t e
T1
60
t
T1
400
300
40
h1( t )
w 1( t )200
20
100
0
0.2
0
0.2
t
0.4
0.6
0
0.2
0
0.2
t
0.4
0.6
82. Немінімально-фазові ланки Квазіаперіодична першого порядку
6. Частотні характеристики6.1 Амплітудно-частотна
A
k1
T1 2 1
6.2 Фазо-частотна
arctgT1
5
180
4
90
3
A 1( )
1( )
2
90
1
0
100
0
50
0
50
100
180
100
50
0
50
100
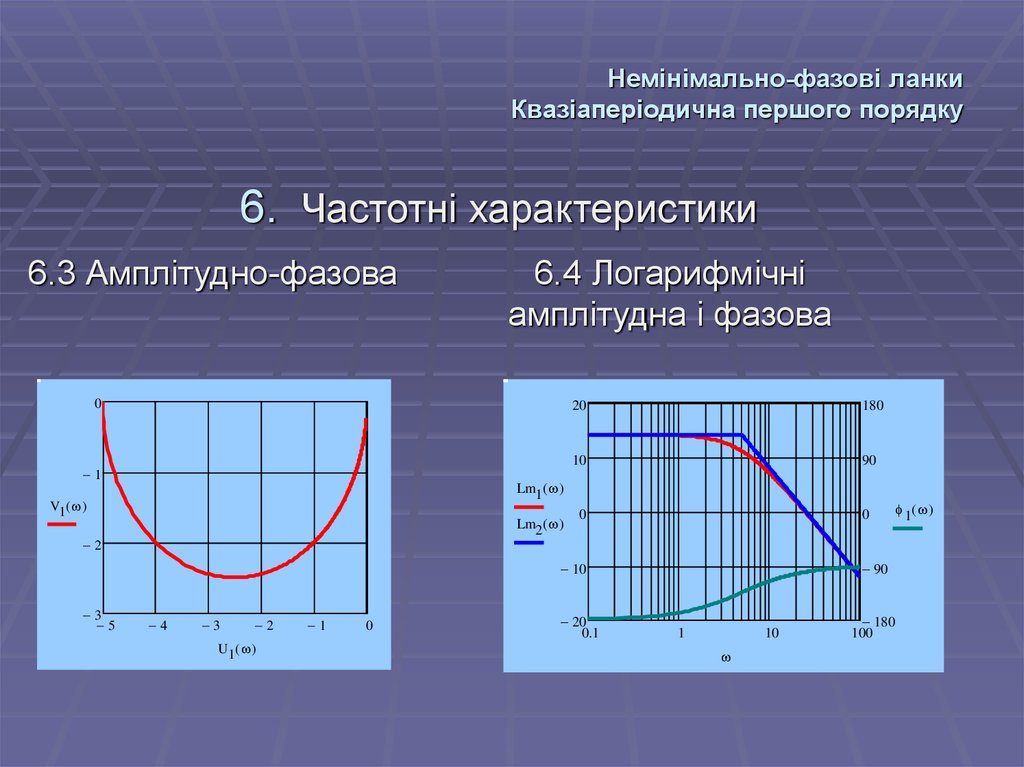
83. Немінімально-фазові ланки Квазіаперіодична першого порядку
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
0
1
20
180
10
90
0
0
Lm1( )
V1( )
Lm2( )
2
10
3
5
4
3
2
U 1( )
1
0
20
0.1
90
1
10
180
100
1( )
84. Немінімально-фазові ланки Квазіаперіодична першого порядку
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
0
0
1
1
2
U 1( )
V1( )
3
2
4
5
3
0
20
40
60
80
100
0
20
40
60
80
100
85. Немінімально-фазові ланки Квазіколивальна
1. Рівняння динамікиt 2 T2 x t x t k1 g t
T22 x
2. Рівняння динаміки в операторному вигляді
T p
2
2
2
2 T2 p 1 x k1g
3. Передаточна функція
W p
k1
T22p2 2 T2p 1
4. Частотна передаточна функція
k1
W j 2
2
T2 j 2 j T2 1
86. Немінімально-фазові ланки Квазіколивальна
5. Часові характеристики5.1 Перехідна функція
h t k 1 e
1 2
t
T2
e
1 2
t
T2
40
5.2 Вагова функція
1 2
w t k 1
e
T2
1 2
e
T2
100
30
75
h( t ) 20
w ( t ) 50
10
25
0
1 2
t
T2
0
0.2
0.4
0.6
t
0.8
0
0
0.2
0.4
0.6
t
0.8
1
1 2
t
T2
87. Немінімально-фазові ланки Квазіколивальна
6. Частотні характеристики6.1 Амплітудно-частотна
6.2 Фазо-частотна
k1
A
1 T 2 T
2
2
2 2
arctg
2
2
5
180
4
182.5
3
2 T2
T22 2 1
1( ) 185
A 1( )
2
187.5
1
0
190
0
20
40
60
80
0
20
40
60
80
100
88. Немінімально-фазові ланки Квазіколивальна
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
0
20
90
0.2
0
0
V1( ) 0.4
Lm1( )
20
Lm2( )
0.6
40
0.8
5
4
3
2
U 1( )
1
0
60
0.01
90 1( )
180
0.1
1
10
270
100
89. Немінімально-фазові ланки Квазіколивальна
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
0
0
1
0.2
2
U 1( )
V1( ) 0.4
3
0.6
4
5
0.8
0
20
40
60
80
100
120
0
20
40
60
80
100 120
90. Немінімально-фазові ланки Коливальна з від'ємним демпфіруванням
1. Рівняння динамікиT22 x
t 2 T2 x t x t k 1 g t
2. Рівняння динаміки в операторному вигляді
T p
2
2
2
2 T 2 p 1 x k 1g
3. Передаточна функція
W p
k1
T22p 2 2 T2p 1
4. Частотна передаточна функція
k1
W j 2
2
T2 j 2 j T2 1
91. Немінімально-фазові ланки Коливальна з від'ємним демпфіруванням
5. Часові характеристики5.1 Перехідна функція
1 2
1 2
T2
h t k 1 1 e t cos
t
sin
2
T
T2
1
2
5.2 Вагова функція
t
w t
k 1
T2 1 2
e
t
T3
1 2
sin
t
T2
60
40
30
20
h( t )
0
w( t )
30
60
0
20
0
1
2
3
t
4
5
40
0
1
2
3
t
4
5
92. Немінімально-фазові ланки Коливальна з від'ємним демпфіруванням
6. Частотні характеристики6.2 Фазо-частотна
6.1 Амплітудно-частотна
A
k1
1 T 2 T
2 2
2
2
arctg
2
2
15
180
10
240
2 T2
T22 2 1
1( )
A 1( )
300
5
360
0
0
20
40
60
80
0
20
40
60
80
93. Немінімально-фазові ланки Коливальна з від'ємним демпфіруванням
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
15
40
180
20
90
0
Lm1( )
20
Lm2( )
40
10
V1( )
5
0
90 1( )
180
60
0
10
5
0
U 1( )
5
10
80
0.01
270
0.1
1
10
360
100
94. Немінімально-фазові ланки Коливальна з від'ємним демпфіруванням
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
10
15
5
10
U 1( )
V1( )
0
5
5
10
0
0
20
40
60
80
100
120
0
20
40
60
80
100 120
95. Немінімально-фазові ланки Квазіколивальна з від'ємним демпфіруванням
1. Рівняння динамікиT22 x
t 2 T2 x t x t k 1 g t
2. Рівняння динаміки в операторному вигляді
T p
2
2
2
2 T 2 p 1 x k 1g
3. Передаточна функція
W p
k1
T22p 2 2 T2p 1
4. Частотна передаточна функція
k1
W j 2
2
T2 j 2 j T2 1
96. Немінімально-фазові ланки Квазіколивальна з від'ємним демпфіруванням
5. Часові характеристики5.1 Перехідна функція
h t k 1 e
1 2
t
T2
e
1 2
t
T2
5.2 Вагова функція
1 2
w t k 1
e
T2
1 2
t
T2
1 2
e
T2
250
80
200
60
150
w( t )
h( t ) 40
100
20
0
50
0
0.2
0.4
0.6
t
0.8
0
0
0.2
0.4
0.6
t
0.8
1
1 2
t
T2
97. Немінімально-фазові ланки Квазіколивальна з від'ємним демпфіруванням
6. Частотні характеристики6.1 Амплітудно-частотна
k1
A
1 T 2 T
2
2
2 2
2
6.2 Фазо-частотна
arctg
2
5
2 T2
T22 2 1
170
4
172.5
3
A 1( )
1( ) 175
2
177.5
1
0
180
0
20
40
60
80
100
0
20
40
60
80
100
98. Немінімально-фазові ланки Квазіколивальна з від'ємним демпфіруванням
6. Частотні характеристики6.3 Амплітудно-фазова
0.4
0.3
20
90
0
0
Lm1( )
20
Lm2( )
V1( )0.2
90 1( )
40
0.1
0
5
6.4 Логарифмічні
амплітудна і фазова
4
3
2
U 1( )
1
0
60
0.01
180
0.1
1
10
270
100
99. Немінімально-фазові ланки Квазіколивальна з від'ємним демпфіруванням
6. Частотні характеристики6.5 Дійсна
6.6 Уявна
0
0.4
1
0.3
2
U 1( )
V1( )0.2
3
0.1
4
5
0
0
20
40
60
80
100
120
0
20
40
60
80
100
100. Позиційні ланки Квазіконсервативна
1. Рівняння динамікиT12 x
t x t k 1 g t
2. Рівняння динаміки в операторному вигляді
T p
2
1
2
1 x k 1g
3. Передаточна функція
W p
k1
T12p 2 1
4. Частотна передаточна функція
k1
W j 2
2
T1 j 1
101. Позиційні ланки Квазіконсервативна
5. Часові характеристики5.1 Перехідна функція
5.2 Вагова функція
t
t
k 1 T1
T1
h t
e e
2
h( t )
t
t
k 1 T1
T1
w t
e e
2T1
100
500
75
375
w( t ) 250
50
125
25
0
0
0
0.5
1
t
1.5
2
0
0.5
1
t
1.5
2
102. Позиційні ланки Квазіконсервативна
6. Частотні характеристики6.2 Фазо-частотна
6.1 Амплітудно-частотна
k1
A
1 T22 2
10
0
8
45
6
1( ) 90
A 1( )
4
135
2
0
0
20
40
60
80
100
180
0
20
40
60
80
100
103. Позиційні ланки Квазіконсервативна
6. Частотні характеристики6.3 Амплітудно-фазова
6.4 Логарифмічні
амплітудна і фазова
1
180
0.5
V1( )
90
0
0
Lm1( )
0
Lm2( )
0.5
1
10
50
50
5
0
U 1( )
5
10
100
0.01
1( )
90
0.1
1
10
180
100
104. Позиційні ланки Квазіконсервативна
6. Частотні характеристики6.5 Дійсна
U 1( )
6.6 Уявна
10
1
5
0.5
V1( )
0
0
5
0.5
10
1
0
20
40
60
80
100
0
20
40
60
80
100

































































































 informatics
informatics








