Основные понятия геометрической оптики

1. Лекция 1 (3сем). Оптика-1

Курс физики для студентов БГТУ
Заочный факультет
для специальностей ЛИД, ТДП, ТДПС, МОЛК, МОЛКС
Часть V.
Оптика
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Лекция 1 (3сем).
Оптика-1
1. Общие сведения о световых волнах. Показатель преломления
среды. Законы геометрической оптики.
2. Интерференция света. Интенсивность света при суперпозиции
двух монохроматических волн. Время и длина когерентности.
Способы получения когерентных волн. Оптическая длина пути и
оптическая разность хода.
3. Интерференция в тонких пленках. Полосы равной толщины и
равного наклона.
4. Кольца Ньютона. Просветление оптики. Применение
интерференции.
2017
1
+4

2. 1. Основные понятия геометрической оптики

Оптика - раздел физики, занимающийся изучением природы света, закономерностей
его испускания, распространения и взаимодействия с веществом.
Геометрической оптикой называют часть оптики, в которой изучаются законы
распространения света в прозрачных средах на основе представления о свете как о
совокупности световых лучей.
Изотропная среда – среда, световые характеристики которой (прежде всего скорость
света в ней) одинаковы по разным направлениям.
Для характеристики изотропной среды, в которой распространяется свет, вводится
понятие показателя преломления.
Абсолютный показатель преломления равен
скорость
с света в вакууме больше скорости v света в среде.
• в среде
v
n = c/v и показывает во сколько раз
μ>1 и ε>1:
1
0 0
• для неферромагнетиков
μ≈1:
c
- меньше с
n
Относительный показатель преломления n21 - отношение абсолютного показателя
второй среды к абсолютному показателю первой, т. е. n21 = n2 /n1 .
Среда с бόльшим показателем преломления называется оптически бόлее плотной.
Оптическая длина пути
L для однородной среды равна произведению показателя
преломления n на длину геометрического пути l: L = nl.
2
+9

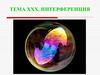
3. Основные законы геометрической оптики

При падении света на границу раздела двух диэлектриков возникают
отражённая и преломлённая волны, подчиняющиеся законам отражения
и преломления (смотри рисунок).
Плоскость падения световой волны - это плоскость, в которой
лежат падающий (1), отражённый (2) и преломлённый (3), лучи,
а также перпендикуляр в точке падения.
На рисунке плоскость падения = плоскость экрана (желтая).
Закон отражения света:
1
2
n1
n2
1
2
3
падающий и отраженный лучи, а также перпендикуляр к границе
раздела двух сред, восстановленный в точке падения луча, лежат в
одной плоскости (плоскость падения).
Угол отражения
γ равен углу падения α.
Закон преломления света: отношение синуса угла
падения α к синусу угла преломления β есть величина
постоянная, равная отношению абсолютного
показателя преломления второй среды n2 к абсолютному
показателю преломления первой среды n1 (из которой
падает свет):
При переходе света из оптически
более плотной среды в оптически
менее плотную n2 < n1 (например,
из стекла в воздух) можно
наблюдать явление полного
отражения, то есть исчезновение
преломленного луча.
3
+5

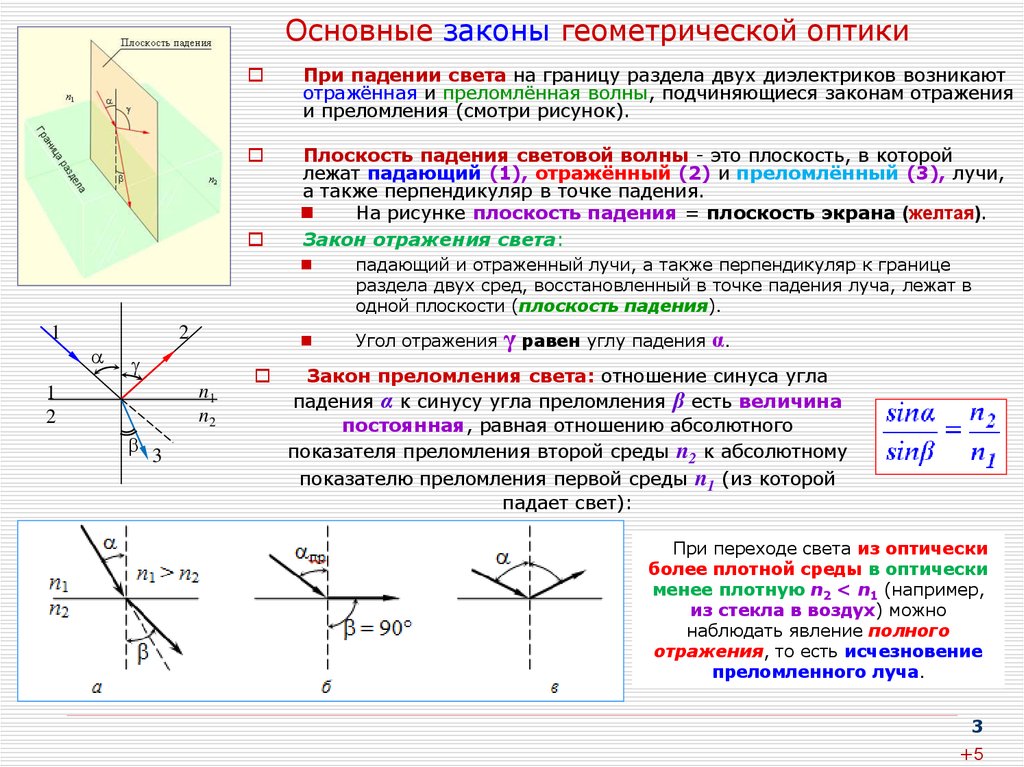
4. Явление полного внутреннего отражения. Световоды

Явление наблюдается при углах падения, превышающих некоторый
критический угол αпр, который называется предельным углом
полного внутреннего отражения. Для угла падения
sin β = 1; тогда значение sin αпр = n2 / n1 < 1.
α = αпр имеем
Если второй средой является воздух (n2 ≈ 1), то формулу удобно переписать в виде:
n = n1 > 1 – абсолютный показатель преломления первой среды.
sin αпр = 1 / n, где
Для границы раздела стекло–воздух (n = 1,5) критический угол равен αпр = 42°, для границы вода–
воздух (n = 1,33) αпр = 48,7°.
Явление полного внутреннего отражения используется в световодах, представляющих собой
тонкие, произвольным образом изогнутые нити (волокна) из оптически прозрачного материала.
Из световодов изготовляются гибкие зонды, с помощью которых свет можно передавать на
расстояние практически по любой траектории и позволяющие видеть, диагностировать, например,
4
поверхность цилиндра автомобильного двигателя, внутренность желудка и т. п.
+5

5. 2. Явление интерференции световых волн

Интерференционная картина
при наложении
(суммировании)
2-х волн
Интерференция света – это явление наложения
(суперпозиции) волн от двух или нескольких когерентных
источников, в результате которых происходит устойчивое
перераспределение энергии этих волн в пространстве.
В области перекрытия волн колебания налагаются друг на
друга, происходит сложение волн, в результате чего
колебания в одних точках пространства получаются с
бόльшей амплитудой (усиливаются – светлые области),
а в других – с меньшей амплитудой (ослабляются – темные
области).
В каждой точке среды результирующее колебание будет суммой всех
колебаний, дошедших до данной точки.
Результирующее колебание в каждой точке среды имеет постоянную во времени амплитуду,
зависящую от расстояний точки среды от источников колебаний.
Такого рода сложение колебаний называется
источников.
интерференцией от когерентных
Рассмотрим сложение (суперпозицию) в некоторой точке М
пространства двух световых волн от точечных источников S1 и S2,
циклические частоты гармонических колебаний которых равны ω1 и ω2, а
начальные фазы – соответственно α1 и α2.
где Е01 и Е02 амплитудные значения светового вектора, 1 и 2 циклические частоты
колебаний, k1 и k2 волновые числа волн, r1 и r2 расстояния от источников волн до точки
5
наложения. Фазы колебаний φ1 и φ2 , а начальные фазы α1 и α2 .
+7

6. Когерентные волны и источники. Разность фаз

Луч от источника S1 распространяется в среде с показателем
преломления n1, а луч от источника S2 – в среде с показателем
преломления n2.
Пусть вызываемые ими колебания в произвольной точке М одинаково
направлены и удовлетворяют уравнениям: E1 = E0 1 sinφ1 и E2 = E0 2
sinφ2
По принципу суперпозиции, результирующее колебание в точке
М описывается формулой E= E1 + E2 = E0sinφ
Методом векторных диаграмм (рис. слева снизу) получим:
Возможны два случая:
а) разность фаз волн φ2 – φ1 в точке М изменяется с течением
времени. Такие волны и возбуждающие их источники S1 и S2
называются некогерентными;
б) разность фаз волн φ2 – φ1 не зависит от времени; такие волны
и возбуждающие их источники называются когерентными.
Определение: Когерентными называются такие волны и возбуждающие их источники, у
которых разность фаз остается постоянной с течением времени
Δφ=φ2 – φ1 = const.
Разность фаз:
Вспомним, что волновое число:
где v – фазовая
скорость волны
Тогда Разность фаз:
6
+10

7. Следствие 1: Монохроматические волны и источники

Второе и третье слагаемые правой части этого равенства не зависят от времени.
Поэтому две синусоидальные волны когерентны, если их циклические частоты
одинаковы ω1 = ω2, и некогерентны, если их частоты различны.
Вспомним, что циклическая частота:
Следствие 1: раз при наложении когерентных синусоидальных волн их
циклические частоты одинаковы ω2 = ω1, то одинаковы и линейные частоты
ν2 = ν1 и длины испускаемых волн: λ2 = λ1 - такие волны называются
монохроматичными.
Определение: Монохроматичными называются такие волны и возбуждающие
их источники, у которых длина волны остается постоянной с течением
времени λ = const.
Значит предпосылки наблюдения устойчивой интерференционной
картины
1) Волны должны быть когерентными,
2) Волны должны быть монохроматичными,
7
+6

8. Следствие 2: Суммирование некогерентных волн

Из формулы:
Следствие 2: при наложении (суммировании) некогерентных синусоидальных волн
амплитуда E0 результирующих колебаний в произвольной точке М среды зависит от
времени, т. е. результирующие колебания негармонические.
Циклическая частота колебаний ωрезульт амплитуды E0 совпадает с циклической частотой
изменения
φ1 – φ2 т. е. равна ωрезульт=|(ω2 – ω1)|.
Если эта частота достаточно велика, то любой регистрирующий свет прибор не будет
успевать реагировать на изменения величины E0, т. е. будет показывать лишь некоторое ее
среднее значение.
Найдем среднее значение квадрата амплитуды <E0>2 за время, равное периоду τ ее
изменения:
Вывод: при наложении
(суммировании)
некогерентных волн
интерференции нет.
За достаточно большое время τ последнее слагаемое интеграл обращается в ноль.
8
+7

9. Суммирование некогерентных волн. Оптическая разность хода

Вывод: при наложении (суммировании)
некогерентных волн среднее значение квадрата
амплитуды результирующей волны равно сумме
квадратов амплитуд исходных волн.
Известно, что освещенность пропорциональна квадрату амплитуды волны.
Поэтому освещенность в данном месте пространства при наложении некогерентных волн
будет равномерной и определяется суммой освещенности от двух источников.
Следствие 3: волны, излучаемые независимыми источниками света, некогерентны.
т.к. фазы
времени.
φ излучения атомов вещества меняются случайно за короткий промежуток
Из формулы:
где для когерентных волн
ω2 = ω 1 = ω
α2 = α 1
Вспомним, что
фазовая скорость:
Оптическая разность хода
Следствие 4: Для устойчивой картины интерференции надо, чтобы оптическая
разность хода
Δ когерентных волн была постоянна (Δ=const).
9
+9

10. 2. Условия интерференционных минимумов и максимумов

Из формулы:
Но интенсивность I излучения
пропорциональна квадрату
амплитуды колебаний:
Для некогерентных волн:
интерференционный член для Е и I
за период
колебаний Т
Вывод: при наложении когерентных волн распределение интенсивности I по пространству
неоднородное и зависит от радиус-векторов данной точки пространства относительно источников.
Интенсивность достигает максимума во всех точках пространства, в которых:
Условие интерференционного
максимума:
где
Если интенсивности равны:
Интенсивность возрастает
10
+14

11. 2. Условия интерференционных минимумов и максимумов

Из формулы:
Интенсивность достигает минимума во всех точках пространства, в которых:
Отсюда получим условие
интерференционного
минимума:
где
Если интенсивности равны:
Интенсивность
падает до нуля
Вывод 1: интерферировать могут только монохроматические когерентные волны, если им
соответствуют колебания, совершающиеся вдоль одного и того же или близких направлений.
В опытах, поставленных Френелем и Араго, было показано, что когерентные световые волны со
взаимно перпендикулярными плоскостями поляризации интерференционной картины
(чередования максимумов и минимумов) не создают.
Вывод 2: При интерференции волн отсутствует простое суммирование их энергий.
Интерференция волн приводит к перераспределению энергии колебаний между
соседними областями среды. Однако в среднем для достаточно большой области
пространства энергия результирующей волны равна сумме энергий интерферирующих волн.
11
Поэтому явление интерференции не противоречит закону сохранения и превращения
+12
энергии.

12. Как выглядит интерференционная картина

Условие интерференционного
максимума:
где
Условие интерференционного
минимума:
где
На фото показаны интерференционные полосы
для синего света
для красного света
для белого света
12
+6

13. 3. Интерференция на тонких пленках

Интерференцию света по методу временного
разделения наблюдать проще, чем в опытах
с пространственным разделением.
Один из способов, использующих такой метод,
– опыт Поля, в котором свет от источника S
отражается двумя поверхностями тонкой
прозрачной плоскопараллельной пластинки.
В любую точку P, находящуюся с той же
стороны от пластинки, что и источник,
приходят два луча.
Эти лучи образуют интерференционную
картину.
Для определения вида полос можно представить себе, что лучи выходят из мнимых
изображений S1 и S2 источника S, создаваемых поверхностями пластинки.
На удаленном экране, расположенном параллельно пластинке, интерференционные
полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке,
проходящем через источник S.
Этот опыт предъявляет менее жесткие требования к размерам источника S, чем
рассмотренные выше опыты.
Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с
малым отверстием, что обеспечивает значительный световой поток.
С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую
интерференционную картину прямо на потолке и на стенах аудитории.
Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше
расстояние между полосами.
13
+10

14. Полосы равного наклона

Особенно важен частный случай
интерференции света, отраженного двумя
поверхностями плоскопараллельной
пластинки, когда точка наблюдения P находится
в бесконечности, т.е. наблюдение ведется либо
глазом, аккомодированным на бесконечность,
либо на экране, расположенном в фокальной
плоскости собирающей линзы.
В этом случае оба луча, идущие от S к P,
порождены одним падающим лучом и после
отражения от передней и задней поверхностей
пластинки параллельны друг другу.
Обозначения на рисунке:
n = n2 – показатель преломления материала пластинки; предполагается,
что над пластинкой находится воздух, т.е. nвозд = n1 = 1.
h – толщина пластинки,
αиβ
– углы падения и преломления на верхней грани, причем:
Так как:
и
Оптическая разность хода между ними в точке P такая же,
как на линии DC:
Тогда для оптической разности хода:
14
+7

15. Полосы равного наклона -2

Следует также учесть, что при отражении волны
от верхней поверхности пластинки ее фаза
изменяется на
π:
Поэтому добавочная разность хода складываемых
волн в точке P равна:
где
Полная оптическая разность хода складываемых волн в
точке P равна:
Полоса данного порядка интерференции обусловлена светом, падающим на пластинку под одним и
тем же углом
λ – длина волны в вакууме
α.
Поэтому такие полосы называют полосами равного наклона, которые можно наблюдать через
линзу, которая обеспечивает схождение лучей в фокальной плоскости.
Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических
колец с центром в фокусе, причем в центре картины порядок интерференции максимален.
15
+6

16. Цвета тонких пленок

В белом свете интерференционные полосы, при отражении от тонких пленок окрашены. Поэтому такое явление называют цвета тонких пленок.
Его легко наблюдать:
на мыльных пузырях,
на тонких пленках масла или
бензина, плавающих на поверхности
воды,
на пленках окислов, возникающих на
поверхности металлов при закалке
(цвета побежалости),
и т.п.
Изменение интерференционной картины поверхности мыльного
пузыря по мере уменьшения толщины мыльной пленки
Почему происходят изменения?
Под действием силы тяжести мыльная пленка постепенно стекает вниз, истончаясь.
16
+9

17. 3. Кольца Ньютона

Примером полос равной толщины являются кольца Ньютона.
Кольца Ньютона – это кольцевые полосы равной толщины,
наблюдаемые в воздушном зазоре между соприкасающимися
выпуклой сферической поверхностью линзы малой кривизны и
плоской поверхностью стекла.
Общий центр колец расположен в точке касания.
В отраженном свете в центре находится темное пятно (минимум
нулевого порядка). Оно окружено системой чередующихся светлых и
темных концентрических колец, ширина, интенсивность которых
постепенно убывают по мере удаления от центрального пятна.
В проходящем свете наблюдается дополнительная картина –
центральное пятно светлое, следующее кольцо темное и т. д.
Оптическая разность хода волн, отраженных от воздушного зазора
(n=1):
где – угол
α малый (значит: sinα→0), h– толщина воздушного зазора мала
по сравнению с R (h2 →0).
Толщина h воздушного зазора связана с расстоянием r до точки касания:
Приравняем h к условию
максимумов:
17
+9

18. Кольца Ньютона - 2

Используя условие максимумов и
минимумов можно найти радиусы
темных и светлых колец в
отраженном свете:
условие максимумов:
условие минимумов:
Внимание: в проходящем свете
эти формула меняются местами –
первая определяет радиусы светлых
колец, а вторая - темных.
Кольца Ньютона локализованы в очень малой области для обычных
линз, поэтому их приходится рассматривать в микроскоп.
При облучении светом одной длины волны будем наблюдать светлые
кольца одного цвета, при облучении белым светом - разноцветные
кольца.
Если линзу постепенно отодвигать от поверхности стекла, то
интерференционные кольца будут стягиваться к центру.
При увеличении расстояния на λ/2 картина принимает прежний вид,
так как место каждого кольца будет занято кольцом следующего порядка.
Этим методом, как и в опыте Юнга, можно сравнительно простыми
средствами приближенно определить длину волны света.
С помощью колец Ньютона можно с достаточно высокой точностью
контролировать качество изготовления сферических поверхностей.
Выводы:
1. Полосы равного наклона получаются при освещении пластинки постоянной толщины
(h=const) рассеянным светом, в котором содержатся лучи разных направлений.
2. Полосы равной толщины наблюдаются при освещении пластинки переменной
толщины (клина) (h≠const) параллельным пучком света.
Полосы равной толщины локализованы вблизи пластинки.
18
+13

19. Просветлённая оптика

2
1
Возможность ослабления отраженного света вследствие
интерференции в тонких пленках широко используется в современных
оптических приборах (фотоаппаратах, биноклях, перископах и др.).
Для этого на передние поверхности имеющихся в них линз и призм
наносят тонкие прозрачные пленки, абсолютный показатель
преломления
n которых меньше абсолютного показателя преломления
для материала линзы или призмы (nплёнки< nстекла).
nплёнки<nстекла
Идея уменьшения интенсивности отраженного света от поверхности
оптических деталей состоит в интерференционном гашении волны,
отраженной от внешней поверхности детали 1, волной отражённой от
внутренней 2.
Для осуществления этого амплитуды обеих волн должны быть
равны, а фазы отличаться на 180°. В этом случае обеспечивается
гашение отражённой волны. Такая оптика получила название
просветленной оптики.
Необходимое соотношение между фазами отражённых волн
обеспечивается выбором толщины плёнки dпл, кратной нечётному
числу четвертей длины волны проходящего через рассматриваемую
деталь света: dпл=(2m-1)λ0/4
Добиться одновременного гашения для всех длин волн
невозможно, то толщина пленки подбирается такой, чтобы
интерференционный минимум был для λ0=555 нм (зеленый свет),
соответствующей интенсивности естественного света.
В отраженном свете просветленные линзы и призмы кажутся
окрашенными в фиолетовый цвет, так как они заметно отражают
только красный и сине–фиолетовый свет.
19
+7

20. Спасибо за внимание!

Курс физики для студентов БГТУ
Заочный факультет
для специальностей ЛИД, ТДП, ТДПС, МОЛК, МОЛКС
Кафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть V.
Оптика
Спасибо за внимание!
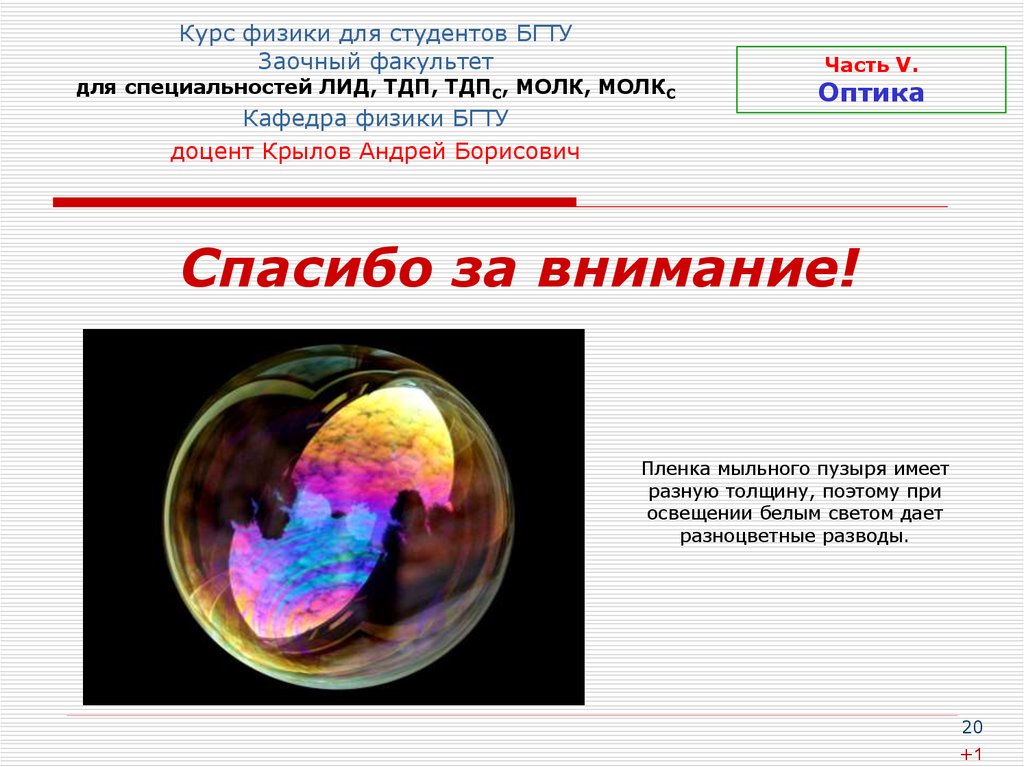
Пленка мыльного пузыря имеет
разную толщину, поэтому при
освещении белым светом дает
разноцветные разводы.
20
+1