Similar presentations:
Тригонометрические неравенства
1. Решение простейших тригонометрических неравенств.
РЕШЕНИЕ ПРОСТЕЙШИХТРИГОНОМЕТРИЧЕСКИХ
НЕРАВЕНСТВ.
2. Тригонометрические неравенства
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
неравенства cost >a,
cost ≥ a, cost <a, cost ≤ a
неравенства sint >a,
sint ≥ a, sint <a, sint ≤ a
3. Неравенство sint > a Алгоритм решения
НЕРАВЕНСТВО SINT > AАЛГОРИТМ РЕШЕНИЯ
1. Отметить на оси ординат
y
1
интервал y > a.
2.Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
t1
π-t1
a
0
-1
x
обход дуги ( против часовой
стрелки)
4.Записать числовые
значения граничных точек, при
этом начало дуги- меньшее
значение
5. Записать общее решение
неравенства.
4.
05.05.20203
sin x
2
1. На Оу отмечаем значение
3
0 ,8
2
и соответствующие точки на
окружности.
2. Выделяем верхнюю часть
окружности (обход совершаем
против часовой стрелки).
y
2
2
x
4
3
3
2
3
3. Подписываем полученные точки. Обязательно учитываем,
что начало дуги – меньшее значение.
4
2 k ;
2 k
4. Ответ: х
3
3
4
5. Неравенство sint ≤ a Алгоритм
НЕРАВЕНСТВО SINT ≤ AАЛГОРИТМ
1. Отметить на оси ординат
y
1
t1
a
0
-1
интервал y≤a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
3π-t1
обход дуги ( против часовой
стрелки)
x 4.Записать числовые
значения граничных точек,
при этом начало дугименьшее значение
4. Записать общее решение
неравенства.
6.
2sin x
2
05.05.2020
y
2
1. На Оу отмечаем значение
0 ,7
2
и соответствующие точки на
окружности.
2
5
4
2
2
4
2
2. Выделяем нижнюю часть
окружности (обход совершаем
против часовой стрелки).
x
3. Подписываем полученные точки. Обязательно учитываем,
что начало дуги – меньшее значение.
5
2 k ; 2 k
4. Ответ: х
4
4
6
7. Неравенство cost > a Алгоритм решения
НЕРАВЕНСТВО COST > AАЛГОРИТМ РЕШЕНИЯ
-1
t1
y
a
0
-t1
1. Отметить на оси абсцисс
интервал x > a.
2. Выделить дугу окружности,
соответствующую интервалу.
3. Выбрать положительный
обход дуги ( против часовой
стрелки)
4 Записать числовые значения
1 x
точек t1 и t2 , учитывая, что
начало дуги –меньшее значение.
5. Записать общее решение
неравенства.
8.
2cos x
2 y
1. На Ох отмечаем значение
2
0 ,7
2
и соответствующие точки на
окружности.
05.05.2020
2
3
4
2. Выделяем правую часть
окружности (обход совершаем
2
против часовой стрелки).
2
2
x
3
4
3. Подписываем полученные точки. Обязательно учитываем,
что начало дуги – меньшее значение.
3
3
2 k ;
2 k
4. Ответ: х
4
4
8
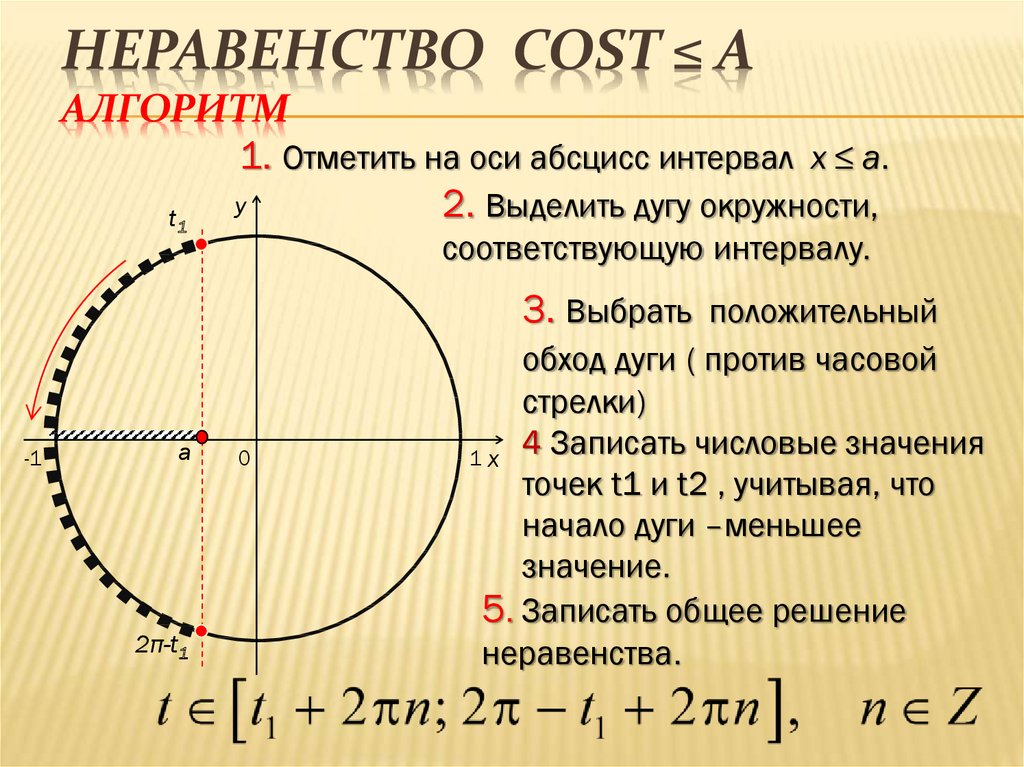
9. Неравенство cost ≤ a Алгоритм
НЕРАВЕНСТВО COST ≤ AАЛГОРИТМ
1. Отметить на оси абсцисс интервал x ≤ a.
y
2. Выделить дугу окружности,
t1
соответствующую интервалу.
3. Выбрать положительный
-1
a
2π-t1
0
обход дуги ( против часовой
стрелки)
4 Записать числовые значения
1x
точек t1 и t2 , учитывая, что
начало дуги –меньшее
значение.
5. Записать общее решение
неравенства.
10.
1cos x
2
1. На Оx отмечаем значение
и соответствующие точки на
окружности.
1
2
05.05.2020
y
2
3
1
2
2. Выделяем левую часть
окружности (обход совершаем
против часовой стрелки).
2
x
5
3
3. Подписываем полученные точки. Обязательно учитываем,
что начало дуги – меньшее значение.
4. Ответ:
5
х 2 k ;
2 k
3
3
10
11. Литература
05.05.2020ЛИТЕРАТУРА
1.Бородуля И.Т. Тригонометрические уравнения и
неравенства –М.Просвещение
2. http://edu-teacherzv.ucoz.ru










 mathematics
mathematics








