Основы логики

1. Основы логики

2.

Логика – это наука о формах и способах
мышления.
В логике мышление рассма-тривается как
инструмент познания окружающего мира.

3. Этапы развития логики

1-й этап связан с работами ученого и
философа Аристотеля (384-322 гг. до
н.э.). Он пытался найти ответ на вопрос:
«как мы рассуждаем», изучал правила
мышления. Аристотель впервые дал
систематическое изложение логики.
Он подверг анализу человеческое мышление, его
формы – понятие, суждение, умозаключение.
Так возникла формальная логика.

4.

2-й этап – появление математической
логики. Основы ее заложил немецкий
ученый и философ Готфрид Вильгельм
Лейбниц. Он сделал попытку построить
первые логические исчисления,
считал, что можно заменить простые
рассуждения действиями со знаками, и
привел соответствующие правила.

5.

Окончательно развил логику как
науку англичанин Джордж Буль
(1815-1864).
Он
является
основоположником
математической
логики
как
самостоятельной дисциплины.
В его работах логика обрела свой алфавит,
свою орфографию и грамматику.
Недаром начальный раздел математической
логики называют алгеброй логики, или
булевой алгеброй.

6.

Формы мышления
понятие
высказывание
умозаключение

7. Понятие

-
это форма мышления, фиксирующая
основные,
существенные
признаки
объекта.

8. Высказывание

- это форма мышления, в которой что-либо
утверждается или отрицается о свойствах
реальных предметов и отношениях между
ними.
Высказывание
является
повествовательным
предложением, о котором
можно сказать истинно оно или ложно.

9. Умозаключение

- это форма мышления, с помощью которой
из одного или нескольких суждений
(посылок) может быть получено новое
суждение (заключение).

10. Алгебра высказываний

11.

В алгебре высказываний высказывания
обозначаются именами
логических
переменных, которые могут принимать
лишь два значения: «истина» (1) и «ложь»
(0).
Логические переменные обозначаются
буквами латинского алфавита.
Например:
А=«квадрат – это ромб»
В=«Волга впадает в Черное море»

12.

Элементарные
высказывания
являются
кирпичиками, из которых с помощью
логических операций строятся сложные
высказывания.
Их
иногда
называют
формулами логики высказываний. Наиболее
часто используемые логические операции:
«и», «или», «не».
Например:
1) Число 6 четно или число 8 нечетно
2) Число 6 четно и число 8 нечетно

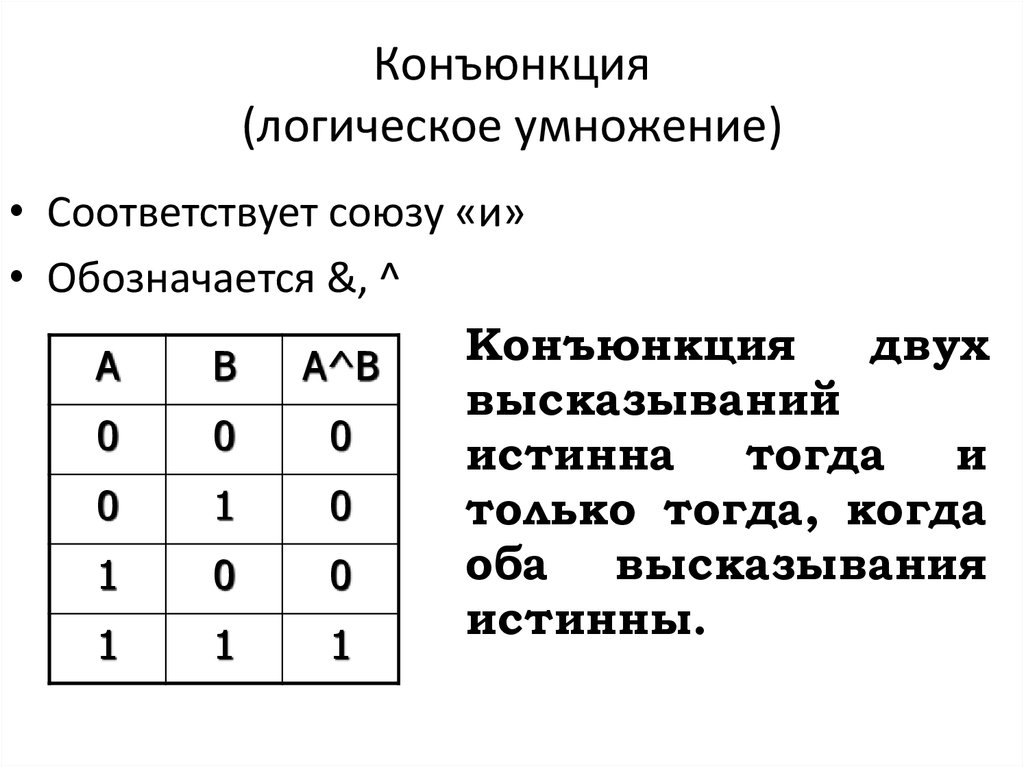
13. Конъюнкция (логическое умножение)

• Соответствует союзу «и»
• Обозначается &, ^
Конъюнкция
двух
А
В
А^В
высказываний
0
0
0
истинна
тогда
и
0
1
0
только тогда, когда
оба высказывания
1
0
0
истинны.
1
1
1

14.

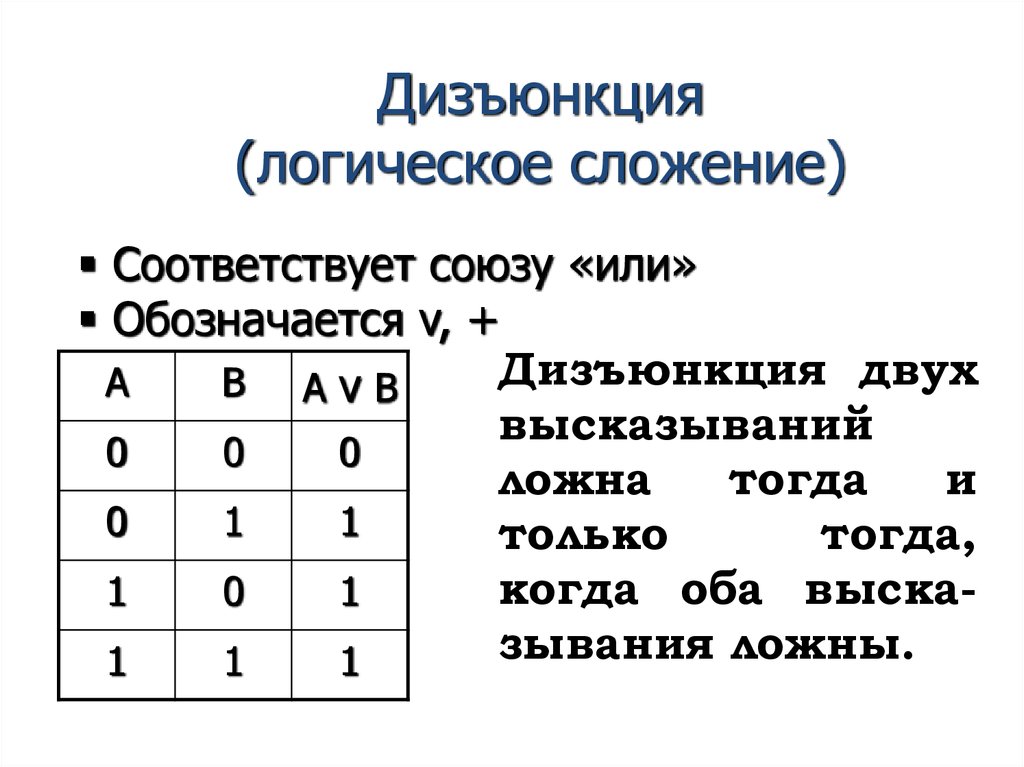
Дизъюнкция
(логическое сложение)
Соответствует союзу «или»
Обозначается v, +
Дизъюнкция двух
А
В АvВ
высказываний
0
0
0
ложна
тогда
и
0
1
1
только
тогда,
когда оба выска1
0
1
зывания ложны.
1
1
1

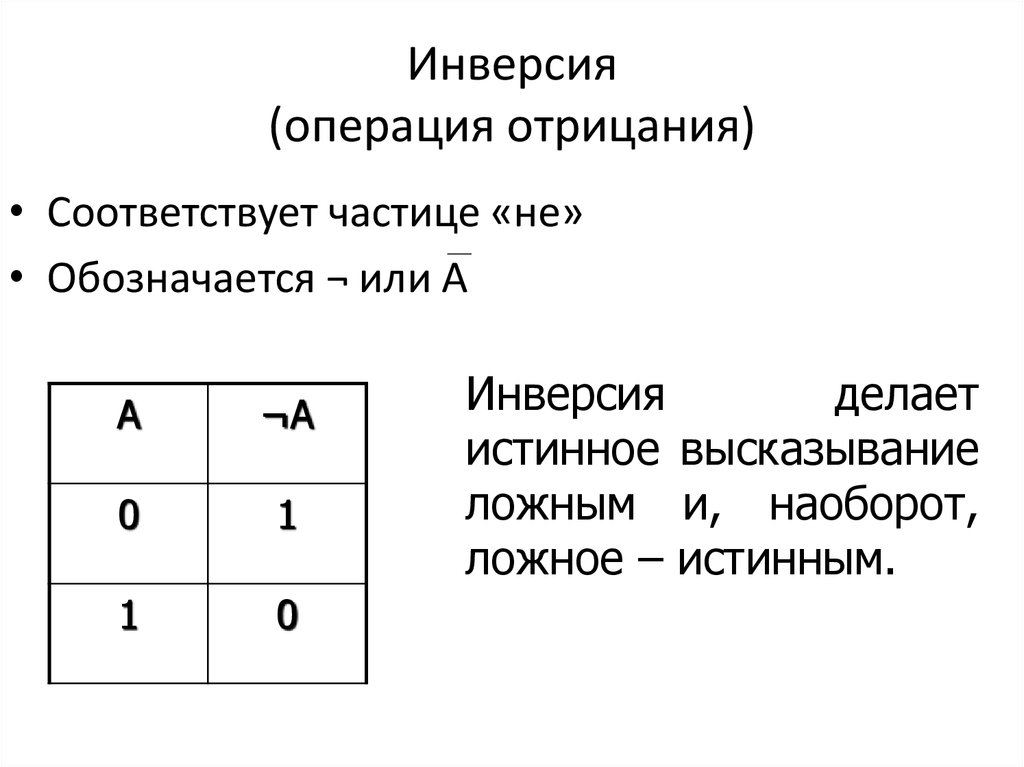
15. Инверсия (операция отрицания)

• Соответствует частице «не»
• Обозначается ¬ или А
А
¬А
0
1
1
0
Инверсия
делает
истинное высказывание
ложным и, наоборот,
ложное – истинным.

16.

А
В
А=>B
0
0
1
0
1
1
1
0
0
1
1
1
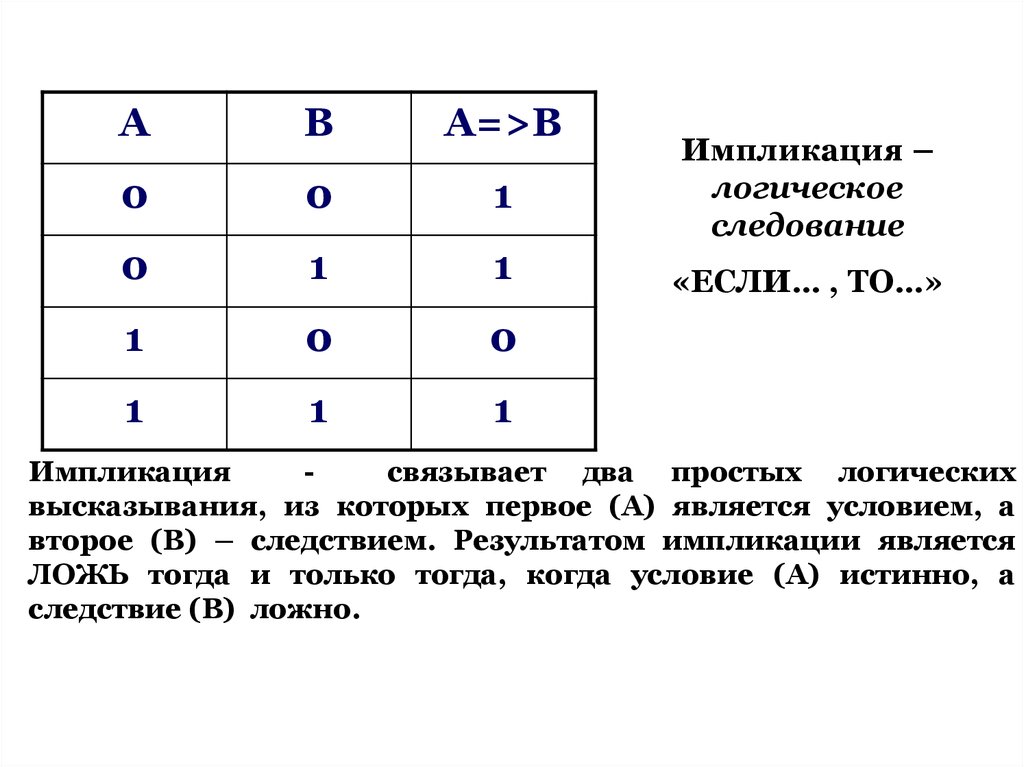
Импликация –
логическое
следование
«ЕСЛИ… , ТО…»
Импликация
связывает два простых логических
высказывания, из которых первое (А) является условием, а
второе (В) – следствием. Результатом импликации является
ЛОЖЬ тогда и только тогда, когда условие (А) истинно, а
следствие (В) ложно.

17.

А
В
А<=>B
0
0
1
0
1
0
1
0
0
1
1
1
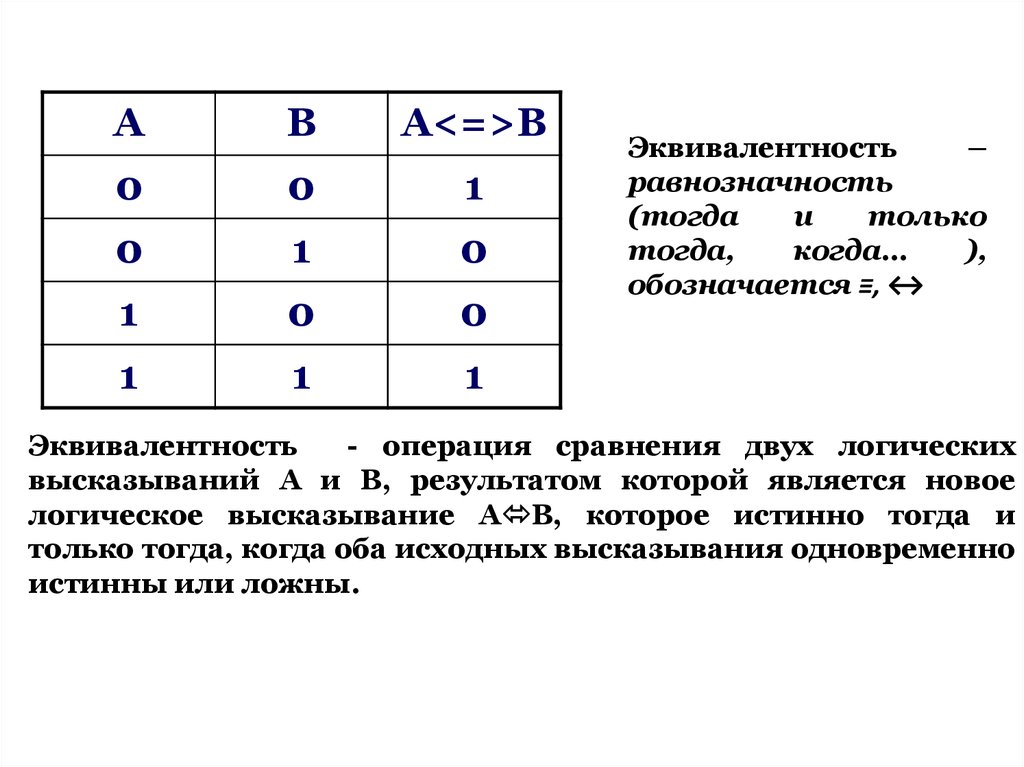
Эквивалентность
–
равнозначность
(тогда
и
только
тогда,
когда…
),
обозначается ≡, ↔
Эквивалентность
- операция сравнения двух логических
высказываний А и В, результатом которой является новое
логическое высказывание А В, которое истинно тогда и
только тогда, когда оба исходных высказывания одновременно
истинны или ложны.

18. Алгоритм построения таблиц истинности

• Определить количество наборов (строк в таблице)
по формуле Q=2n. (n-количество высказываний)
• Разделить колонку значений первой переменной
пополам и заполнить верхнюю половину 0,
нижнюю половину 1.
• В следующей колонке для второй переменной
половину снова делить пополам и заполнить
четырьмя группами 0 и 1, вперемежку, начиная
опять с группы 0 и т.д.

19. Домашнее задание

• выучить материал;
• Составить таблицы истинности для следующих
формул: A&(BvA); (AvB)&(A&B); (A B)≡ (AvC)
• Виктор, Роман, Леонид заняли на олимпиаде по
физике четыре первых места.
Имеются три высказывания:
1. Сергей – первый, Роман – второй
2. Сергей – второй, Виктор – третий
3. Леонид – второй, Виктор – четвертый
Известно, что в каждом варианте только одно
утверждение истинно. Как распределились места?