Основы логики

1. Основы логики

2. ЛОГИКА– это наука о формах и способах мышления

АЛГЕБРА ЛОГИКИ – раздел
математической логики,
изучающий высказывания и
операции над ними.

3. ПОНЯТИЕ – это форма мышления, фиксирующая основные, существенные признаки объекта. ВЫСКАЗЫВАНИЕ – это форма мышления, в которой

что-либо утверждается или отрицается о
свойствах реальных предметов и отношениях
между ними. Высказывание может быть истинно
или ложно.
УМОЗАКЛЮЧЕНИЕ – это форма мышления, с
помощью которой из одного или нескольких
суждений может быть получено новое суждение
(заключение).

4.

Высказывание
В
русском
языке
высказывания
повествовательными предложениями:
Земля вращается вокруг Солнца.
Москва - столица.
Но не всякое
высказыванием
повествовательное
выражаются
предложение
является
Побудительные и вопросительные предложения высказываниями
не являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?

5.

Примеры высказываний
• Москва больше Санкт-Петербурга
• Все мальчики любят играть в футбол
• “Лед - твердое состояние воды” (истинное высказывание)
• “Париж - столица Англии” (ложное высказывание)
• “Все рыбы умеют плавать” (общее)
• “Некоторые медведи - бурые” (частное)
• “Буква А - гласная” (единичное)
• “Кошка является домашним животным.” (?)
• “Некоторые ученики нашего класса двоечники.” (?)
• “Сейчас идет урок рисования” (?)

6. Основные понятия

Константы алгебры логики (булевой
алгебры) – логический 0 (ложь) и
логическая 1 (истина).
Логические переменные принимают
только два значения - логический 0 или
логическая 1.

7. Логической функцией F от набора логических переменных х1,х2,…,хn называется функция, которая может принимать только два

значения:
логический 0 или логическая 1.
Любая логическая функция может быть
задана с помощью таблицы истинности.

8. Элементарные логические операции. Таблицы истинности. Логические схемы.

9. Основные логические операции:

• Конъюнкция, логическое умножение (and - и);
• Дизъюнкция, логическое сложение (or - или);
• Инверсия, логическое отрицание (not - не);
• Импликация (
- следование)(если
высказывание истинно, то…)
• Эквивалентность (~ - тогда и только тогда, когда)
Высказывания в алгебре логики обозначаются
латинскими буквами

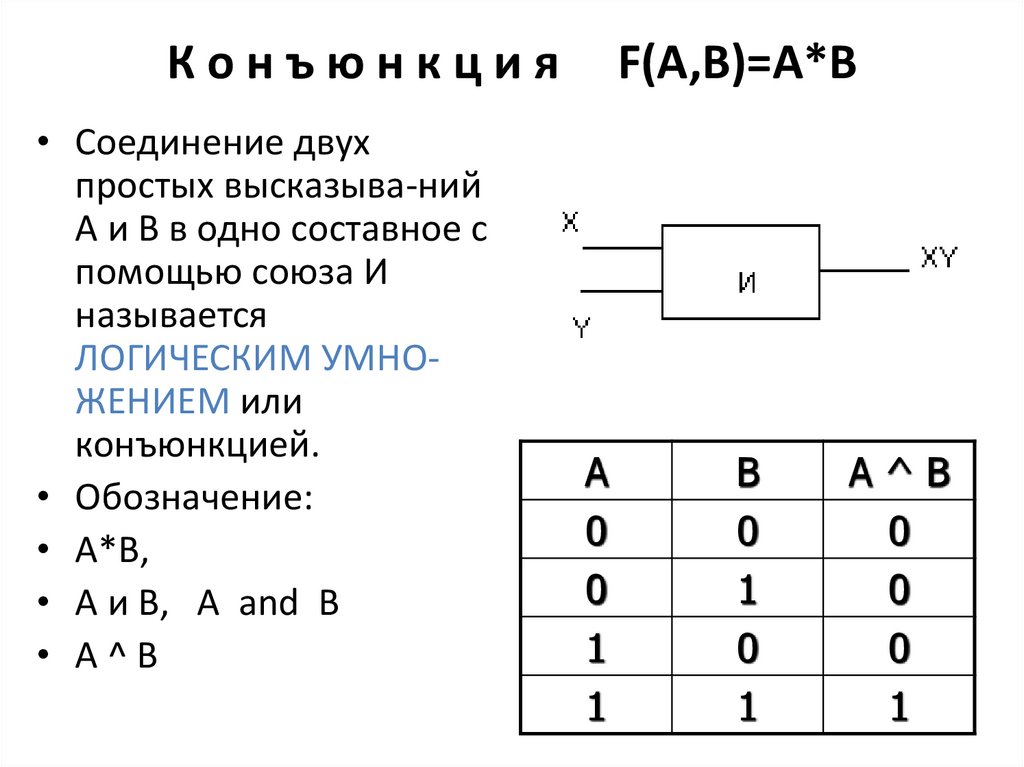
10. К о н ъ ю н к ц и я F(A,B)=A*B

Конъюнкция
• Соединение двух
простых высказыва-ний
А и В в одно составное с
помощью союза И
называется
ЛОГИЧЕСКИМ УМНОЖЕНИЕМ или
конъюнкцией.
• Обозначение:
• А*В,
• А и В, А and В
• А^В
F(A,B)=A*B
А
0
0
1
1
В
0
1
0
1
А^В
0
0
0
1

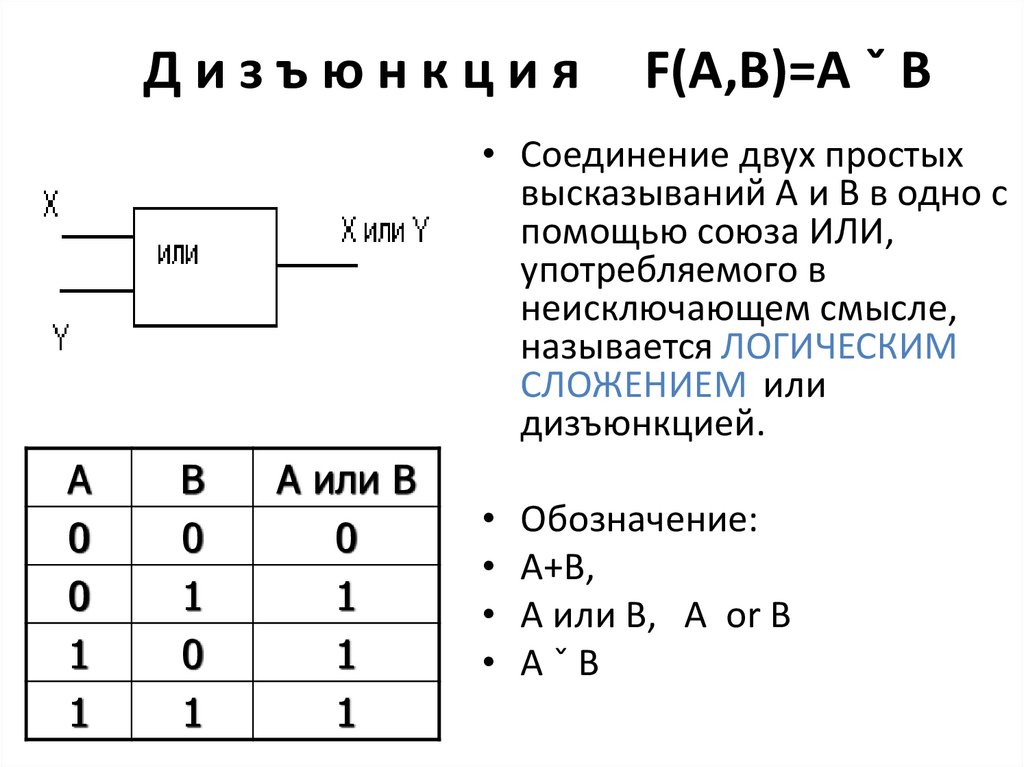
11. Д и з ъ ю н к ц и я F(A,B)=A ˇ B

Дизъюнкция
F(A,B)=A ˇ B
• Соединение двух простых
высказываний А и В в одно с
помощью союза ИЛИ,
употребляемого в
неисключающем смысле,
называется ЛОГИЧЕСКИМ
СЛОЖЕНИЕМ или
дизъюнкцией.
А
0
0
1
1
В
0
1
0
1
А или В
0
1
1
1
• Обозначение:
• А+В,
• А или В, А or В
• АˇВ

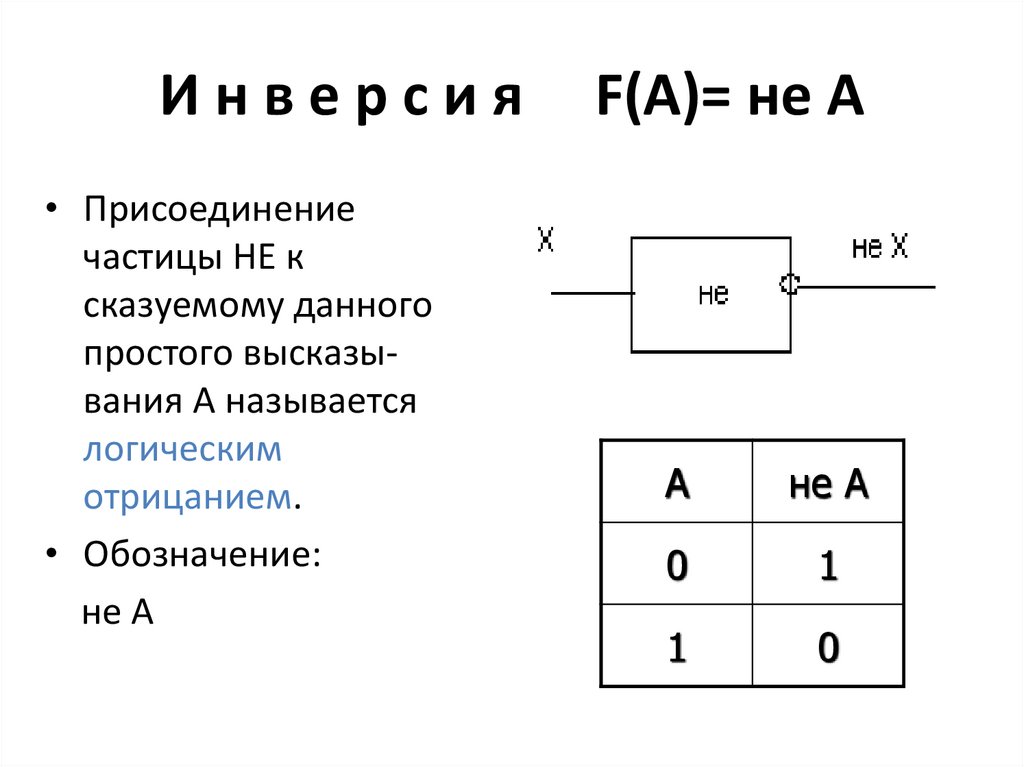
12. И н в е р с и я F(A)= не A

Инверсия
• Присоединение
частицы НЕ к
сказуемому данного
простого высказывания А называется
логическим
отрицанием.
• Обозначение:
не А
F(A)= не A
А
не А
0
1
1
0

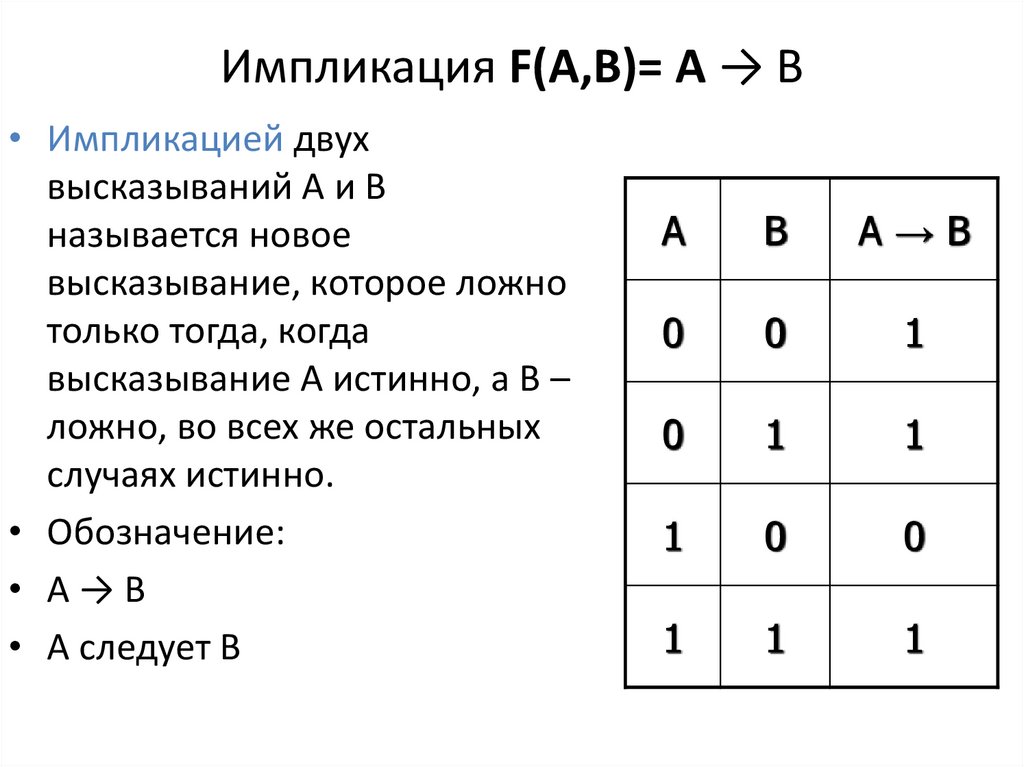
13. Импликация F(A,B)= A → B

• Импликацией двух
высказываний А и В
называется новое
высказывание, которое ложно
только тогда, когда
высказывание А истинно, а В –
ложно, во всех же остальных
случаях истинно.
• Обозначение:
• А→В
• А следует В
А
В
А→В
0
0
1
0
1
1
1
0
0
1
1
1

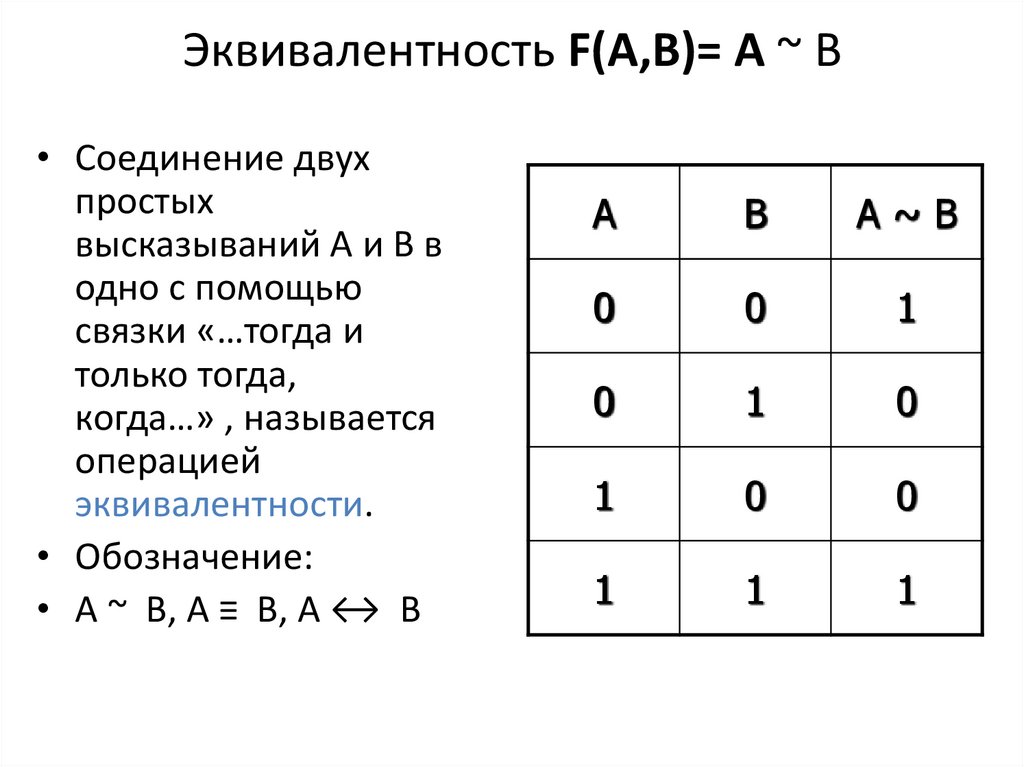
14. Эквивалентность F(A,B)= A ~ B

• Соединение двух
простых
высказываний А и В в
одно с помощью
связки «…тогда и
только тогда,
когда…» , называется
операцией
эквивалентности.
• Обозначение:
• А ~ В, А ≡ В, А ↔ В
А
В
А~В
0
0
1
0
1
0
1
0
0
1
1
1

15. Логические (булевы) выражения -

Это булевы константы и переменные, связанные
логическими операциями И, ИЛИ и НЕ в единую
формулу.

16. Теоремы алгебры логики

• https://zftsh.online/articles/4728

17. СТАРШИНСТВО ЛОГИЧЕСКИХ ОПЕРАЦИЙ :

1. инверсия
2. конъюнкция
3. дизъюнкция
4. импликация
5. эквивалентность
Для изменения порядка действий
используются скобки.

18.

Задание
Даны два простых высказывания:
А = {2 • 2 = 4},
В = {2 • 2 = 5}.
Какие из высказываний истинны:
а) А; б) В; в) A ^ В; г) A v B ;
д) ¬A;
ж) А ^ ¬В?

19.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) A B A
А
В
A
B A
F
0
0
1
0
0
0
1
1
1
1
1
0
0
0
1
1
1
0
0
1

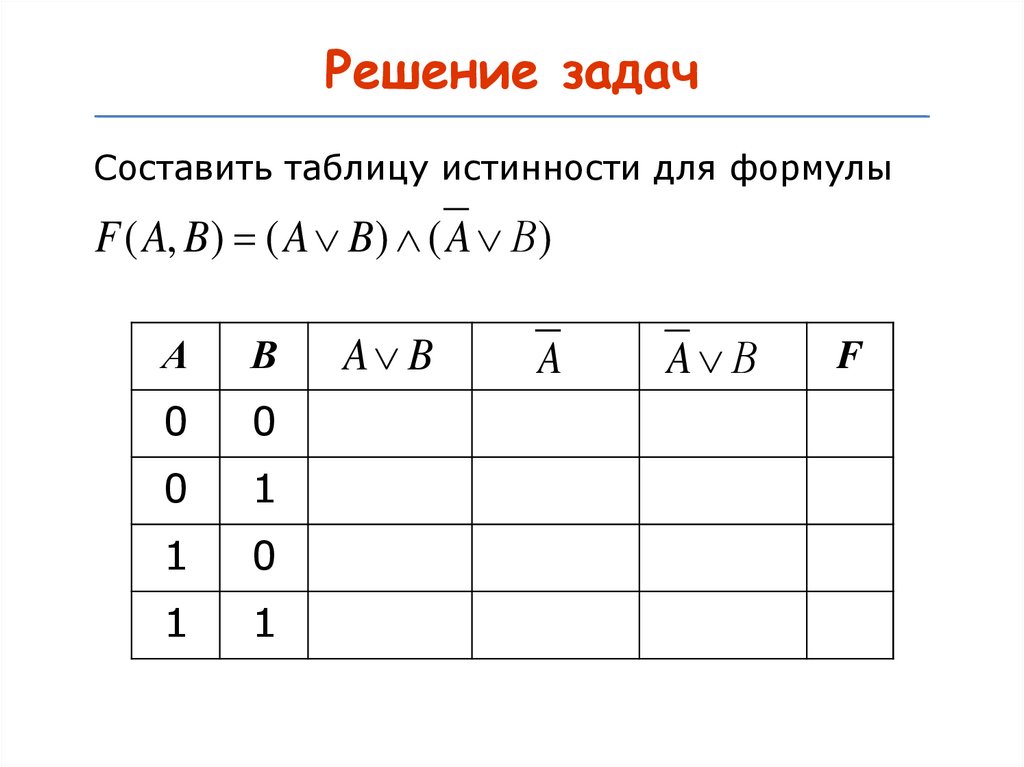
20.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
0
0
0
1
1
0
1
1
A B
A
A В
F

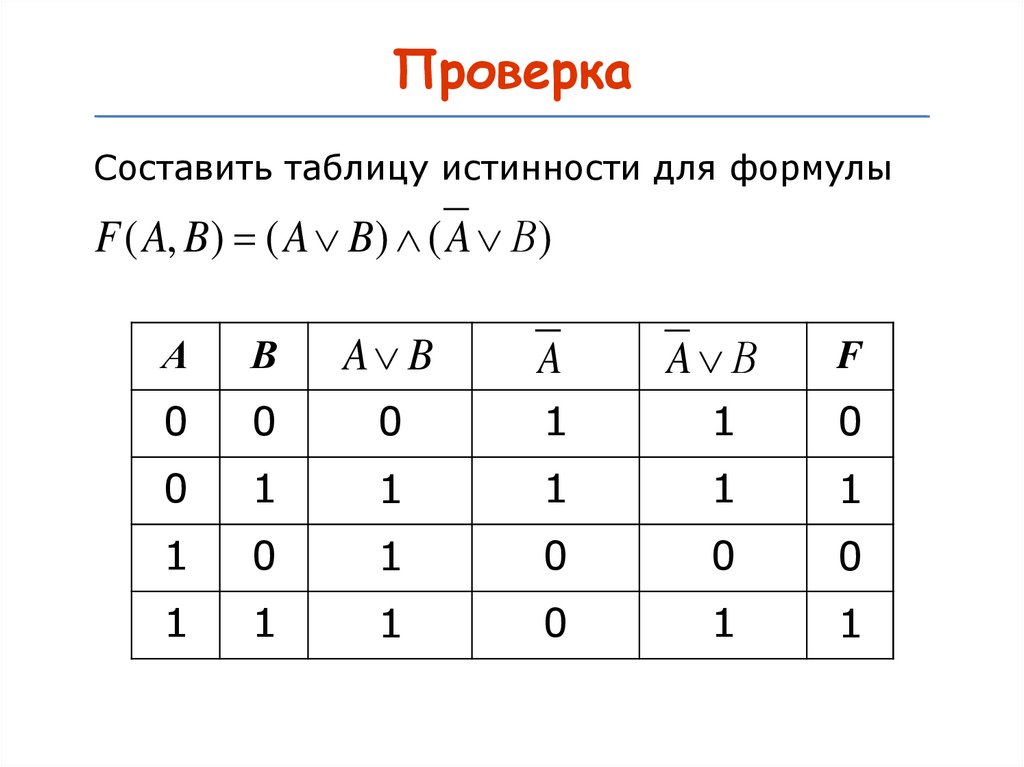
21.

Проверка
Составить таблицу истинности для формулы
F ( A, B) ( A B) ( A В)
А
В
A B
A
A В
F
0
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
0
0
1
1
1
0
1
1

22.

Решение задач
Составить таблицу истинности для формулы
F ( A, B) (( A B) B) ( A B)
x
А
В
0
0
1
1
0
1
0
1
y
В А В ( А В) В А А В
x y
22

23.

Проверка
Составить таблицу истинности
F ( A, B ) (( A B ) B ) ( A B )
x
a
b
0
0
1
1
0
1
0
1
y
В А В ( А В) В А А В
1
1
0
1
1
0
0
1
1
1
1
1
0
0
0
0
1
1
0
1
x y
0
1
0
1
23