Кривые второго порядка на плоскости

1. Курс высшей математики

Часть 1
УГТУ-УПИ
2004г.

2.

Лекция 8.
Кривые второго порядка на плоскости
I. Основные понятия.
2. Исследование формы кривых второго
порядка по их каноническим уравнениям.
3. Приведение уравнений кривых второго
порядка к каноническому виду.

3.

1. Основные понятия.
Алгебраической кривой второго порядка
называется кривая , уравнение которой в декартовой
системе координат имеет вид:
1
Ax 2 2Bxy Cy 2 Dx Ey F 0,
где не все коэффициенты А, В, С равны нулю.

4.

Вырожденные кривые второго порядка :
1. пустое множество
x2 y 2 1 0
2. точка
x2 y 2 0
3. прямая
x 2 2x 1 0 x 1
4. пара прямых
x2 y 2 0 x y
O (0,0)

5.

Т
Всякое уравнение (1), задающее невырожденную
кривую, путём преобразования координат можно
привести к каноническому виду (одному из трех):
2
2
2
2
x
y
2 1 эллипс
I.
2
a b
II .
x
y
2 1 гипербола
2
a b
III .
y 2 2 px парабола

6.

2.
Исследование формы кривых второго порядка
по их каноническим уравнениям.
2.1. Эллипс.
Эллипсом называется кривая второго порядка
с каноническим уравнением
x2
y2
2 1
2
a
b
Если
( x0 , y 0 )
x 0,
( x0 , y 0 ), ( x0 , y 0 ), ( x0 , y 0 ) .
y 0 оси симметрии эллипса (буквой Г
обозначена кривая – эллипс)

7.

Достаточно исследовать кривую и построить её
в области x 0, y 0 ,
достроив затем остальные части путём зеркального
отражения найденных фрагментов кривой
относительно координатных осей.
Так как если
( x0 , y 0 )
, то
( x0 , y0 ) ,
эллипс ,задаваемый каноническим уравнением (I),
имеет центр симметрии, совпадающий с началом
координат О(0,0).
Рассмотрим уравнение эллипса в первой четверти.
I.
y b 1
x2
a2

8.

Y
a
x
b
R
1
F
1
x,y
M
a
x
R2
F
2
a X
Характеристики эллипса
1. a – большая полуось; b – малая полуось.
2. Точки (a,0), ( a,0), (0, b ), (0, b ) - вершины.

9.

3. Точка O 0,0 - центр.
4. Точки
F1 ( c,0), F2 (c,0)
- фокусы, где
Y
a
x
c2 a2 b 2
b
R
1
F
1
x,y
M
a
x
R
2
F
2
a X
5. Числа
R1 , R 2 - фокальные расстояния точки М
6. Число
c
a
эллипса.
- эксцентриситет эллипса.
Чем больше значение , тем больше вытянут эллипс.
0 1

10.

a
7. Прямые x - директрисы эллипса.
Замечание.
Если a b R уравнение I
x2 y 2 R 2
- уравнение окружности радиуса R с центром
в начале координат О(0,0).
Вычислим
R1 R2
x c
2
y
2
x c
2
y 2

11.

R1 R 2 2a
Вывод.
Эллипс является геометрическим местом точек
M x , y , сумма расстояний от которых до двух
заданных точек плоскости F1 c ,0 и F2 c ,0
является постоянной величиной.
Замечание.
Последнее высказывание можно использовать как
определение эллипса. Тогда, используя рисунок,
можно получить каноническое уравнение эллипса.

12.

2.2. Гипербола.
Гиперболой называется кривая второго порядка
с каноническим уравнением
2
2
x
y
2 1
2
a
b
x 0, y 0 - оси симметрии, O 0,0 - центр симметрии.
Рассмотрим уравнение гиперболы в первой четверти.
II .
y b
x2
a2
1

13.

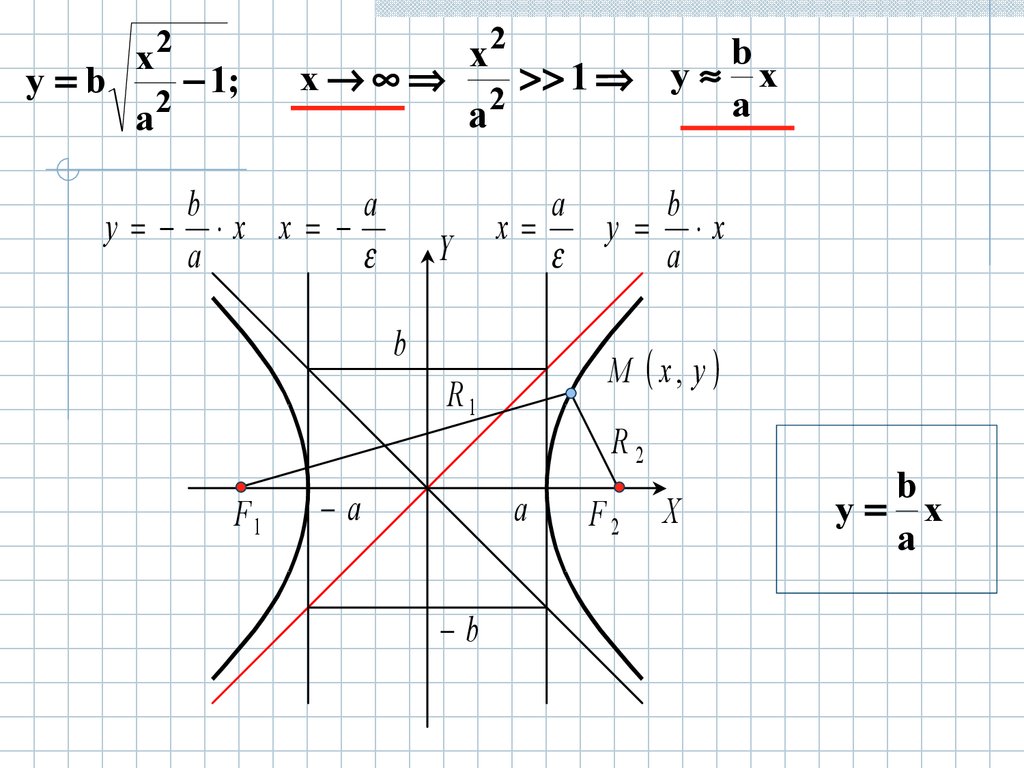
y b
x
2
a
2
1;
x2
b
x 2 1 y x
a
a
b
a
y x x
a
Y
a
x
b
b
y x
a
M x, y
R1
R2
F1
a
a
b
F2
X
b
y x
a

14.

Характеристики гиперболы
1. a – действительная полуось; b – мнимая полуось.
2. Точки (a,0), ( a,0)
y
- вершины.
b
x
a
x
Y
x
b
3. Точка O 0,0 - центр.
4. Точки F1 ( c,0), F2 (c,0)
- фокусы, где c2 a 2 b 2
a
a
y
b
x
a
M x, y
R1
R2
F1
a
a
F2
X
b
5. Числа R1 , R 2 - фокальные расстояния точки М
гиперболы.
6. Число
c
a
- эксцентриситет гиперболы.
1

15.

a
7. Прямые x - директрисы гиперболы.
8. Прямоугольник со сторонами
x a, y b
y
b
a
x x
a
- основной прямоугольник.
b
9. Прямые y a x
– асимптоты гиперболы
a
F
(диагонали основного
прямоугольника).
Вычислим
R1 R2 ( x c) 2 y 2 ( x c) 2 y 2
Y
b
R1 R 2 2a
a
y
b
x
a
M x, y
R1
R2
a
1
x
b
F2
X

16.

Вывод.
Гипербола является геометрическим местом точек
M x , y , модуль разности расстояний от которых
до двух заданных точек плоскости F1 c ,0 и F2 c ,0
является постоянной величиной.
Замечание.
Последнее высказывание можно использовать как
определение гиперболы. Тогда, используя рисунок,
можно получить её каноническое уравнение.

17.

Алгоритм построения чертежа гиперболы.
1. Построение основного прямоугольника.
2. Построение асимптот – диагоналей.
3. Определение вершин гиперболы (выяснение
вопроса о том, какую координатную ось гипербола
2
2
пересекает).
x
y
4. Построение гиперболы.
2
a
2
b
2
x
y
2 2 1
a
b
2
1
Y
b
a
a
b
X

18.

2.3. Парабола.
Параболой называется кривая второго порядка с
каноническим уравнением
y 2 px
2
Прямая
y 0 - ось симметрии (единственная!).
Рассмотрим уравнение параболы в первой четверти.
III .
y 2px

19.

x p /2
Y
d
M x, y
R
p /2
F p / 2 ,0
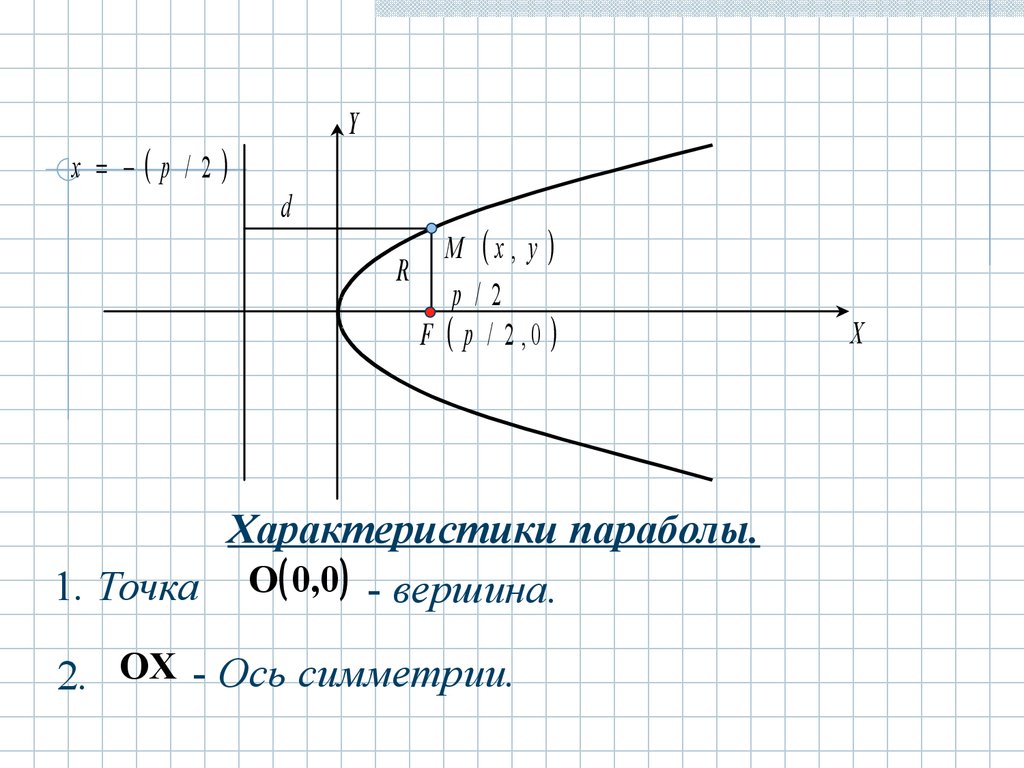
Характеристики параболы.
1. Точка O 0,0 - вершина.
2. OX - Ось симметрии.
X

20.

p
3. Точка F ,0
2
- фокус.
x p /2
Y
d
4. Число R
- фокальный радиус
точки параболы.
M x , y
R
p/2
F p / 2 ,0
p
- директриса.
5. Прямая x
2
Пусть
d - расстояние от точки параболы до
директрисы.
Вычислим
d
d R
X

21.

Вывод.
Парабола является геометрическим местом точек
p
M x , y , равноудаленных от заданной точки F
,
0
2
плоскости и прямой x= -p/2 .
Замечание.
Последнее высказывание можно использовать как
определение параболы. Тогда, используя рисунок,
можно получить её каноническое уравнение.

22.

Канонические уравнения кривых второго порядка
со смещенным центром (вершиной).
I*.
II * .
x x0 2 y y 0 2 1
a2
x x0 2 y y 0 2 1
a2
III * .
b2
b2
y y 0 2 2p x x0

23.

Выполним замену
x x x0
y y y 0
Тогда уравнения
I * . III * .
x , y .
относительно переменных
Геометрически:
OXY
I . III .
O X Y
O 0,0 O x0 , y 0
- параллельный перенос в точку
x0 , y 0 .

24.

Пример.
y 1 2 x 1 2 1
4
9
Тип кривой – гипербола со смещенным в точку (-1,1)
центром. b=2 - действительная полуось, a=3 - мнимая
полуось.
3.
Приведение уравнений кривых второго
порядка к каноническому виду.
Ax 2 2Bxy Cy 2 Dx Ey F 0

25.

Два признака неканоничности:
I . Наличие смешанного произведения xy.
II . Переменные присутствует в уравнении и
в первой, и во второй степени.
Устранение признаков неканоничности:
I.
x x cos y sin
y x sin y cos
Геометрически: OXY
- поворот на угол
O X Y
вокруг точки
O 0,0

26.

II .
x x x 0
y y y 0
Геометрически: O X Y O X Y
O 0,0 O x 0 , y 0
- параллельный перенос в точку x 0 , y 0 .