Similar presentations:
Прикладные задачи, приводящие к задаче линейного программирования. (Лекция 2)
1. Прикладные задачи, приводящие к задаче линейного программирования
Лекция2
Add Your Company
Slogan
Прикладные задачи,
приводящие к
задаче линейного
программирования
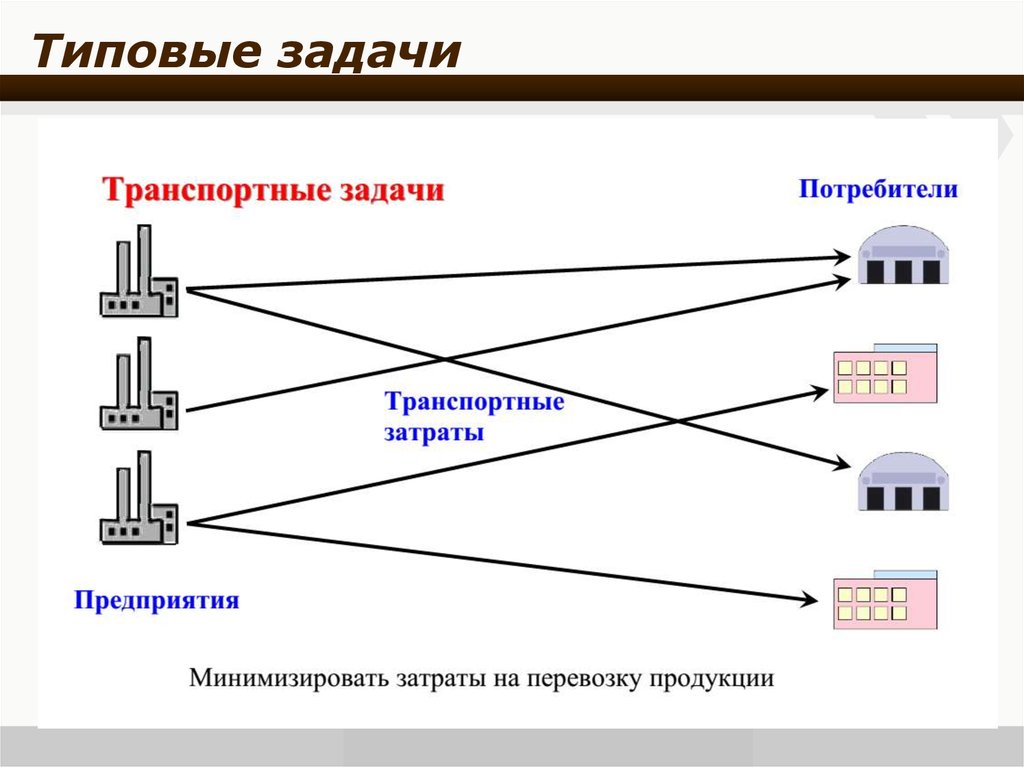
2. Типовые задачи
www.wondershare.com3. Типовые задачи
www.wondershare.com4. Типовые задачи
www.wondershare.com5. Типовые задачи
www.wondershare.com6. Типовые задачи
www.wondershare.com7. Типовые задачи
www.wondershare.com8. Типовые задачи
www.wondershare.com9. Задача об оптимальном использовании ресурсов
n – количество видов выпускаемой продm – количество необходимых для произ
a ij – технологические коэффициенты,
т.е. количество единиц i -го ресурса,
необходимого
для производства
единицы j -го вида продукции
bi – полные объемы имеющихся
ресурсов
Cj
–
прибыль,
получаемая
при
реализации
единицы
j-го
вида
продукта.
x ( x ,..., x ,..., x )
– план
выпуска продукции
n
1
j
n
z c j x j max
j 1
n
a x
j 1
ij
j
bi (i 1, m)
x j 0 ( j 1, n)
www.wondershare.com
10. Задача о смесях
–число необходимых питательных в
– число
продуктов
– количество единиц i-го
a питания
питательного вещества, содержаij щееся в единице j-го вида продукта
– норма потребления i-го
b питания
i питательного вещества
c – цена j-го продукта питания
j
x – количество единиц j-го продукта,
j
используемого
в
рационе,
подлежащее определению
n
z c x min
j j
j 1
n
aij x j bi (i 1, m)
j 1
x 0 ( j 1, n)
j
m
n
www.wondershare.com
11. Задача о назначениях
n – число видов работчисло специалистов, выполняющих все виды работ
n ––эффективность
выполнения i-ым
cспециалистом
ij
j-ой работы
1, i ый человек выполняет j ую работу
xi , j
0, i ый человек не выполняет j ую работу
c
x max
i, j i, j
n
x
j 1
i, j
n
x
i 1
i, j
1 (i 1, n)
1 ( j 1, n)
www.wondershare.com
12. Транспортная задача
m – число пунктов отправления ( Ai – пункт отправлениn – число пунктов назначения( B j – пункт назначения)
ai (i 1, m) – объем продукта в пункте отправления
b j ( j 1, n) – потребность в пункте назначения
c ij
– затраты на перевозку единицы продукта из i-го пункта
отправления в j-ый пункт назначения
m
a
i 1
i
n
b j
j 1
m
n
ai b j(*)
i 1
j 1
Если выполняется условие (*), то перед нами транспортная задача
закрытого типа. В противном случае это – задача открытого типа.
www.wondershare.com
13.
Cоставить такой план перевозок, чтобы общаястоимость перевозок была минимальной.
B1
B2
…
Bn
A1
X11, C11
X12, C12
…
X1n, C1n
A2
X21, C21
X22, C22
…
X2n, C2n
…
…
…
…
…
Am
Xm1, Cm1
Xm2 Cm2
…
Xmn, Cmn
m
n
c
i 1 j 1
x min
ij ij
n
xij ai , (i 1, m)
jm 1
x b , ( j 1, n)
ij
j
i 1
xij 0
www.wondershare.com
14.
Задача линейного программированияцелевая функция;
• система ограничений;
• ограничения на знак переменных
ЗЛП – это задача следующего вида:
n
z x j c j max(min)
j 1
n
aij x j ( , , ) bi
j 1
x 0 ( j 1,l )
j
(i 1,m)
l n
(1)
(2)
(3)
Уравнение (1) – это целевая функция, а (2) и (3) – это
система ограничений.
www.wondershare.com
15.
Задача линейного программированияВектор X ( x , , x ) называется допустимым планом ЗЛП,
1
n
если он удовлетворяет ограничениям (2) и (3).
Вектор X * ( x*, , x* ) называется оптимальным планом ЗЛП,
1
n
если он является допустимым и обеспечивает
минимум или максимум целевой функции.
Множество всех допустимых планов ЗЛП образует
область допустимых значений (ОДЗ).
www.wondershare.com
16.
Каноническая форма записи ЗЛПn
z c x min
j j
j 1
(1)
n
aij x j bi , (i 1,m)
j 1
(2)
В системе ограничений стоят знаки только равенства.
x 0, ( j 1,n)
j
(3)
b 0, (i 1,m)
i
(4)
В системе ограничений присутствует выделенный
исходный базис.
www.wondershare.com













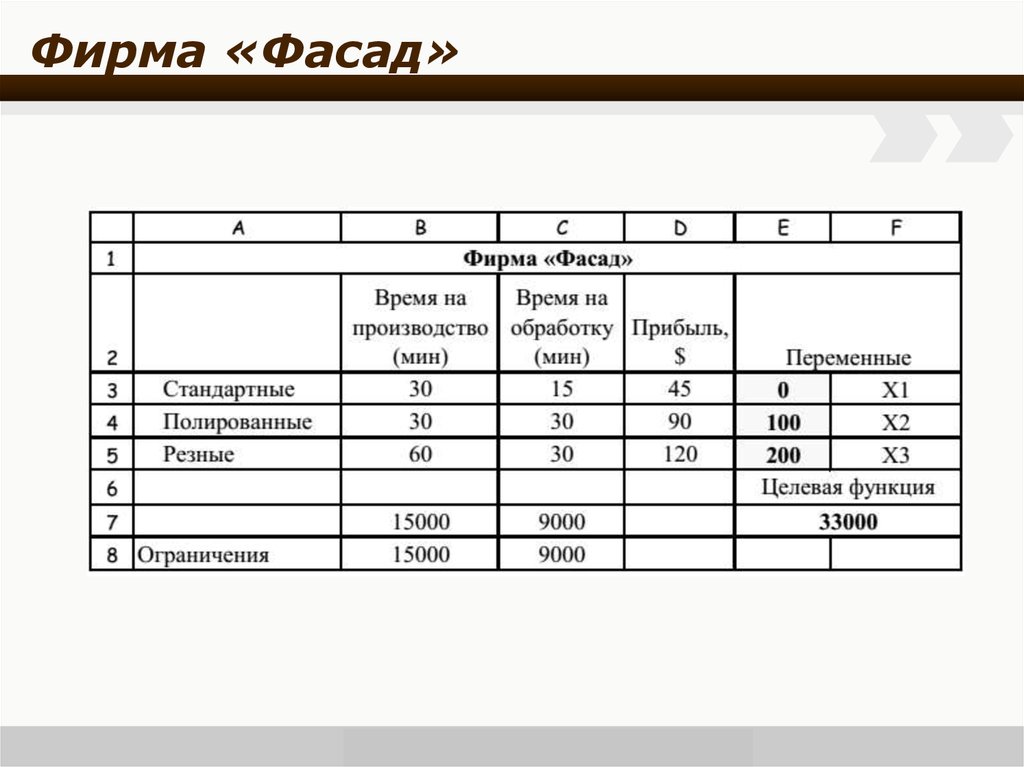
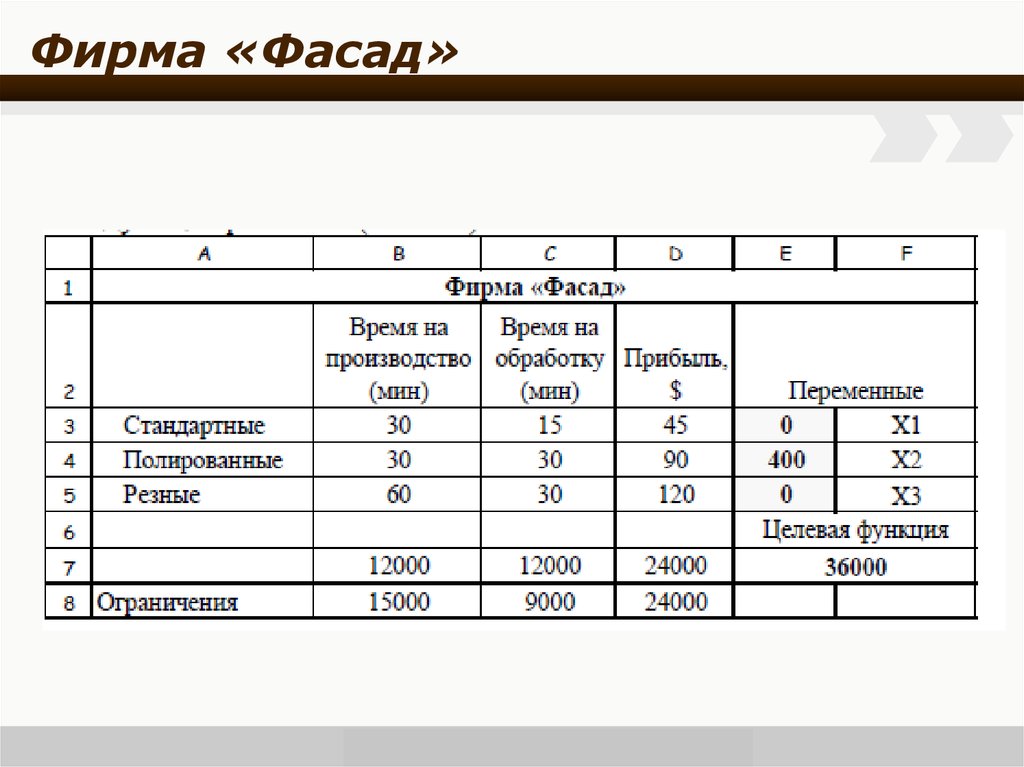

 management
management








