Потенціал електростатичного поля

1. ЕЛЕКТРИКА І МАГНЕТИЗМ Електронний курс лекцій

Укладач: Данилов А.Б.

2.

Хто ні про що не запитує, той
нічому не навчиться.
Томас Фуллер

3.

Лекція 16
Потенціал електростатичного
поля

4.

План лекції
• Робота сил електростатичного поля.
• Циркуляція вектора напруженості.
• Потенціальний характер електростатичного
поля.
• Потенціал електростатичного поля.
• Зв'язок напруженості з потенціалом
електростатичного поля.
• Еквіпотенціальні поверхні.

5.

Лекція 16
Потенціал електростатичного
поля
Робота сил
електростатичного поля
•Елементарна робота сил
електростатичного поля
dA F dl Fdl cos q0 E dl cos
•Для поля точкового заряду
q0 q dr
dA
4 0 r 2

6.

Лекція 16
Потенціал
електростатичного
поля
Робота сил
електростатичного поля
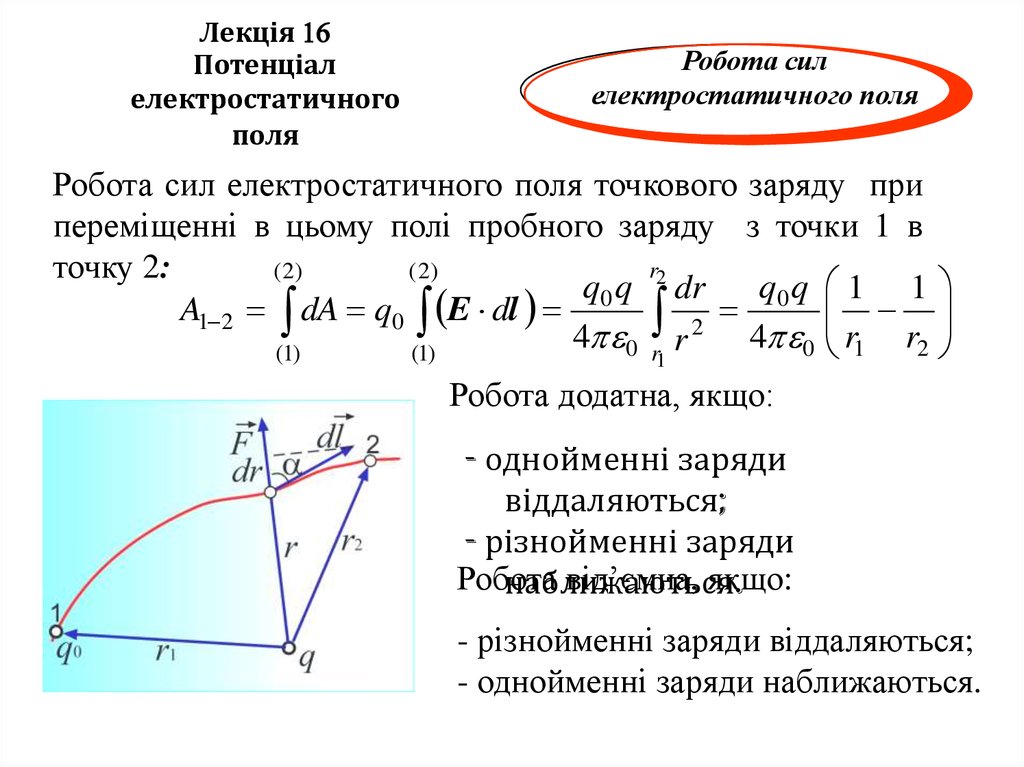
Робота сил електростатичного поля точкового заряду при
переміщенні в цьому полі пробного заряду з точки 1 в
точку 2:
r2
( 2)
( 2)
q0 q dr
q0 q 1 1
A1 2 dA q0 E dl
2
4 0 r r
4 0 r1 r2
(1)
(1)
1
Робота додатна, якщо:
- однойменні заряди
віддаляються;
- різнойменні заряди
Робота
від’ємна, якщо:
наближаються.
- різнойменні заряди віддаляються;
- однойменні заряди наближаються.

7.

Лекція 16
Потенціал
електростатичного
поля
Робота сил
електростатичного поля
Робота електростатичного поля не
залежить від форми шляху переміщення
заряду від точки 1 до точки 2, а
визначається
лише
положенням
початкової і кінцевої точки.
Силові поля, що задовольняють таку
умову, називаються потенціальними, або
консервативними

8.

Лекція 16
Потенціал
електростатичного
поля
Циркуляція вектора
напруженості
Циркуляція
вектора
напруженості
електростатичного поля вздовж довільного
замкненого контуру дорівнює нулеві:
( E dl ) 0
l
Це рівняння називають інтегральною
формою
запису
потенціальності
електростатичного поля.

9.

Лекція 16
Потенціал
електростатичного
поля
Циркуляція вектора
напруженості
Заряд переміщається вздовж
замкненого контуру l
Al dA q0 E dl
l
q0 q
4 0
l
l
dr q0 q 1 1
0
2
4 0 r0 r0
r

10.

Лекція 16
Потенціал
електростатичного
поля
Циркуляція вектора
напруженості
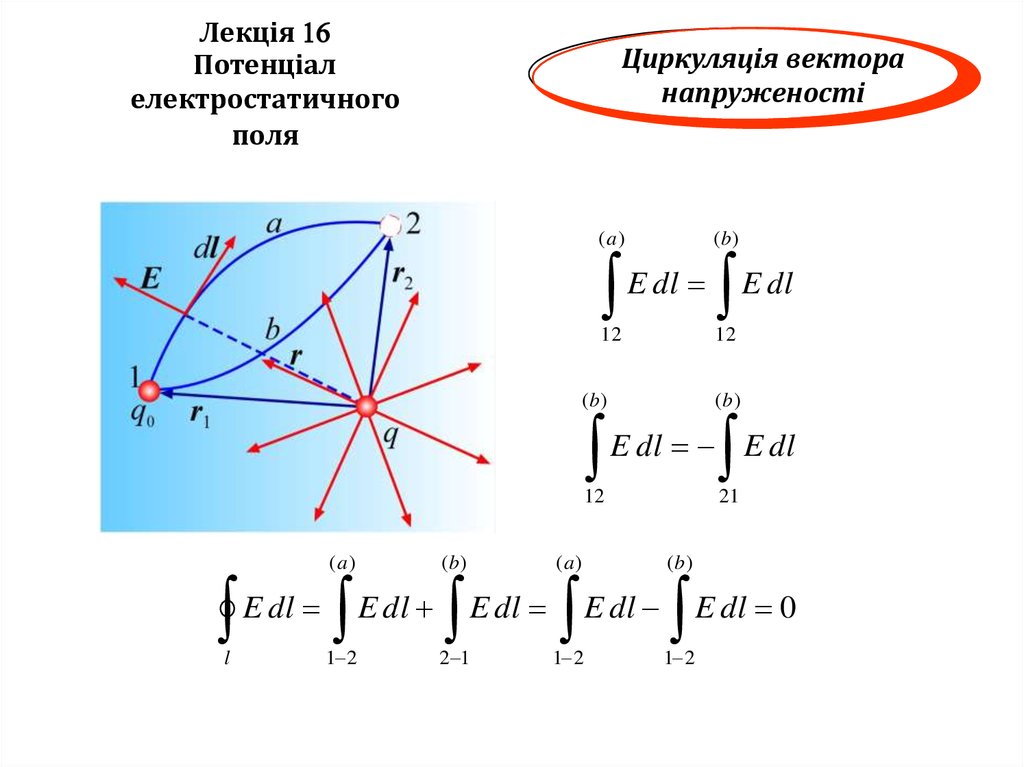
(a)
(b )
E dl
12
E dl
12
(b )
(b )
12
21
E dl E dl
(a)
(b )
(a)
(b )
1 2
2 1
1 2
1 2
E dl E dl E dl E dl E dl 0
l

11.

Лекція 16
Потенціал
електростатичного
поля
Диференціальна форма
потенціальності
• Ротором векторного поля A( r ) називається границя
відношення
Adl
rot A lim l
S 0 S
За математичною теоремою Стокса:
S
(rot A dS ) ( A dl )
l
У декартових компонентах ротор векторного поля запишетьс
ˆi
ˆj
kˆ
Az Ay ˆ Ax Az ˆ Ay Ax ˆ
i
k
rot A
j
x y z y
z z
x
y
x
Ax Ay Az

12.

Лекція 16
Потенціал
електростатичного
поля
Диференціальна форма
потенціальності
Теорема Стокса
для електростатичного поля
S
(rot E dS ) ( E dl ) 0
l
Диференціальна форма
потенціальності електростатичного
поля:
rot E 0
Електростатичне поле є
безвихровим.

13.

Лекція 16
Потенціал
електростатичного
поля
Потенціальна енергія
точкового заряду
Потенціальна енергія точкового заряду q 0 в полі іншого
заряду q
q0 q 1
W
C
4 0 r

14.

Лекція 16
Потенціал
електростатичного
поля
Потенціал
електростатичного
поля
Потенціал електростатичного поля – скалярна фізична
величина, що чисельно дорівнює роботі, яку виконують
сили електростатичного поля при переміщенні пробного
одиничного заряду із заданої точки на нескінченність (або в
точку, потенціал якої можна вважати нульовим).
A1 W1
1
E dl cos
q0
q0 1

15.

Лекція 16
Потенціал
електростатичного
поля
Потенціал
електростатичного
поля
Потенціал 1 В приписують точці поля, при переміщенні з
якої заряду 1 Кл виконується робота 1 Дж:
A 1 Дж
1В
q0 1 Кл
Потенціал поля точкового заряду:
q
(r )
4 0
r
dr
q
2
4 0 r
r

16.

Лекція 16
Потенціал
електростатичного
поля
Потенціал поля
системи зарядів
Потенціал поля системи
точкових зарядів:
( r )
n
i
i 1
n
qi
4 0 i 1 | r ri |
1

17.

Лекція 16
Потенціал
електростатичного
поля
Потенціал
електростатичного
поля
При неперервному розподілі заряду
по об’єму:
1
( r' )
( x , y , z )
dx' dy' dz'
4 0 V | r r' |
1
( r' ) dS
по поверхні:
( x , y , z )
4 0 S | r r' |
1 ( r' ) dl
(
x
,
y
,
z
)
по лінії:
4 0 l | r r' |

18.

Лекція 16
Потенціал
електростатичного
поля
Різниця потенціалів
Різниця потенціалів – скалярна фізична величина, що
визначається роботою переміщення одиничного пробного
заряду q 0
з точки поля з потенціалом 1 у точку з
потенціалом 2
A1 2
U 1 2
q0
Різниця потенціалів між двома довільними точками поля
1 2 ( E dl )
2
1

19.

Лекція 16
Потенціал
електростатичного
поля
Зв’язок напруженості з
потенціалом
dA q0 E x dx
dA q0 ( 1 2 ) q0 d
Ex
x
Ey
y
Ez
z
ˆ ˆ ˆ
E
i
j
k grad
y
z
x
Вектор градієнта спрямований у бік найшвидшого
зростання потенціалу

20.

Лекція 16
Потенціал
електростатичного
поля
Зв’язок напруженості з
потенціалом
Для однорідного поля
1 2 U
E
d
d
Рівняння Пуассона
0
2
2
2
2 2 2
x
y
z
Рівняння Лапласа
- оператор Лапласа
( x , y , z ) 0

21.

Лекція 16
Потенціал
електростатичного
поля
Еквіпотенціальні
поверхні
Геометричне місце точок, потенціали яких є однаковими,
називають
еквіпотенціальними
поверхнями,
або
поверхнями однакового потенціалу.
•Лінії електричного поля і лінії
еквіпотенціальної поверхні взаємно
перпендикулярні;
•Чим густіше проходять лінії, тим
різкіше змінюється потенціал.

22.

Лекція 16
Потенціал
електростатичного
поля
Розрахунок потенціалу
електростатичного
поля
Потенціал поля рівномірно зарядженої
нескінченної площини
E dx
dx
x
2 0
2 0
0
0
x
x
( x ) ( 0)
x
2 0
Потенціал поля між рівномірно зарядженими
нескінченними площинами
E dx dx x
0
0
0 0
x
x
( x) (0) x
0

23.

Лекція 16
Потенціал
електростатичного
поля
Розрахунок потенціалу
електростатичного
поля
Потенціал поля рівномірно зарядженої
нескінченної площини та двох різнойменно
заряджених площин

24.

Лекція 16
Потенціал
електростатичного
поля
Розрахунок потенціалу
електростатичного
поля
Потенціал поля провідної сфери
r
q 1 1
Назовні: ( R) (r )
2
4 0 R r
4 0 r
R
(r )
Всередині:
q
4 0 r
(r ) ( R)
q dr
R2
(r )
0r
q
4 0 R
R
0

25.

Лекція 16
Потенціал
електростатичного
поля
Розрахунок потенціалу
електростатичного
поля
Потенціал поля діелектричної кулі
Назовні:
Всередині:
R 3
(r )
3 0 r
r
2
2
( R) (r )
rdr
(
r
R
)
3 0 R
6 0
(r )
(3R 2 r 2 )
6 0

26.

Лекція 16
Потенціал
електростатичного
поля
Розрахунок потенціалу
електростатичного
поля
Потенціал поля
нескінченно довгого провідного циліндра
r
r
dr
ln
2 0 r
2 0 R
R
r
( R ) ( r ) E dr
R

27.

Лекція 16
Потенціал
електростатичного
поля
Приклад 1
• Знайти потенціал на відстані r від довгого провідного
циліндра радіуса R з лінійною густиною заряду .
Якщо потенціал на нескінченності дорівнює нулеві, то
( R) (r ) ( R) 0
ln
2 0 R
?!!!
Потенціал точки на поверхні циліндра
( R ) ( r )
R
ln 0
2 0 R
?
r0
( R) (r0 ) ( R) 0
ln
2 0 R

28.

Лекція 16
Потенціал
електростатичного
поля
Приклад 2
Додатний електричний заряд , розподілений однорідно вздовж
відрізка довжиною 2а, розташований уздовж осі
між
точками y=-a і y=a. Знайти потенціал електричного поля в
точці на осі x на відстані x від початку координат.
dq (q / 2a ) dy
1
q
d
4 0 2a
1
r
dy
x2 y2
x2 y2
a
q
dy
4 0 2a a x 2 y 2
q x 2 a 2 a
ln
4 0 2a x 2 a 2 a
1

29.

30.

•Він теж радий, що лекція завершилася!