Какие бывают графы

1. Дискретная математика

Какие бывают графы

2. Планарные графы

- Это
графы, допускающие
геометрическую реализацию на
плоскости без пересечения
ребер.
Далеко не все графы являются
планарными.
В трехмерном пространстве можно
геометрически реализовать без
пересечения ребер любой граф.

3. Планарные графы

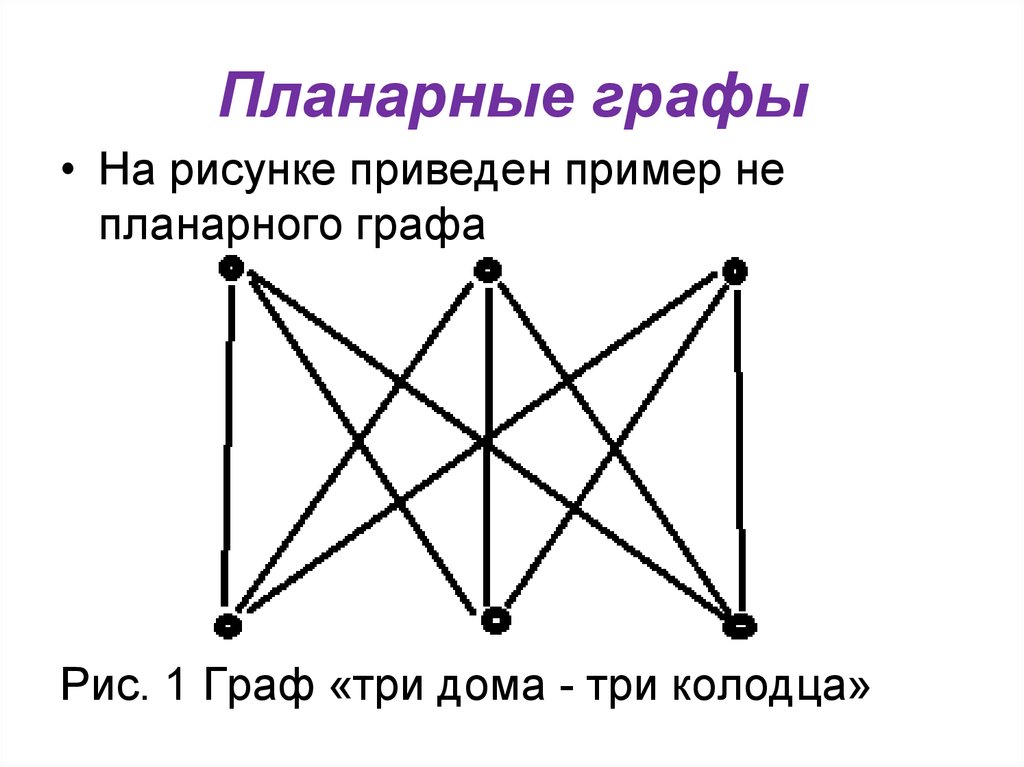
• На рисунке приведен пример не
планарного графа
Рис. 1 Граф «три дома - три колодца»

4. Изоморфные графы

• Графы, отличающиеся только
нумерацией вершин,
называются изоморфными.

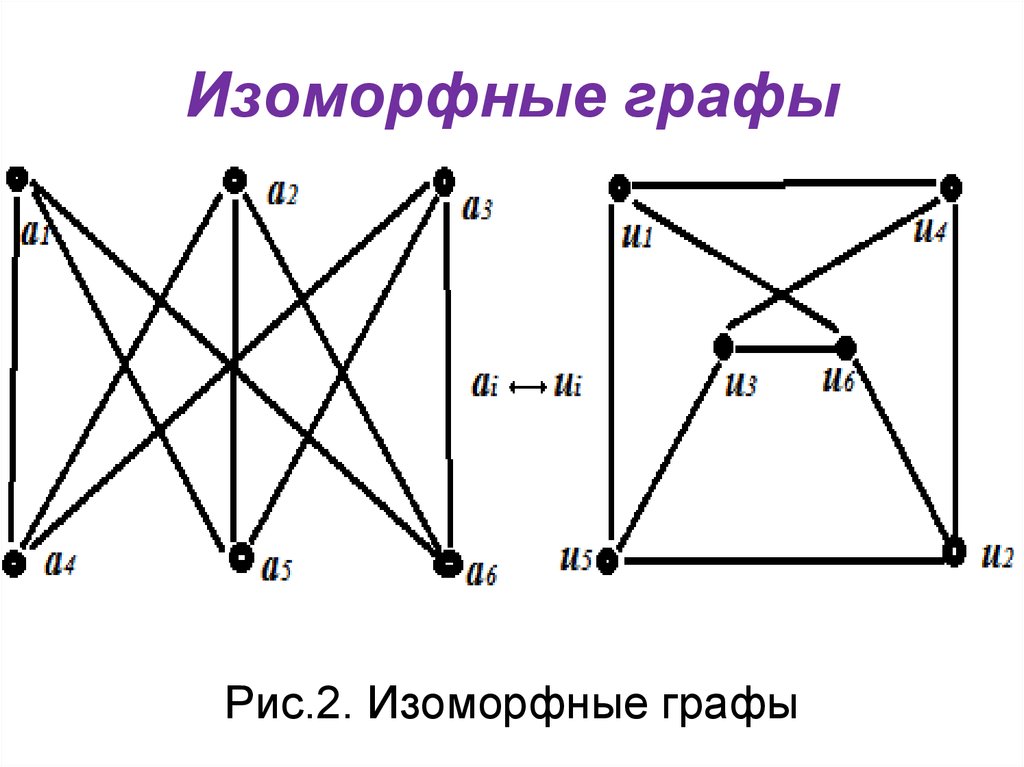
5. Изоморфные графы

Рис.2. Изоморфные графы

6. Пустой и полный граф

• Граф называется пустым,
если множество ребер пусто.
E Ø
Рис. 3. Пустой
граф

7. Пустой и полный граф

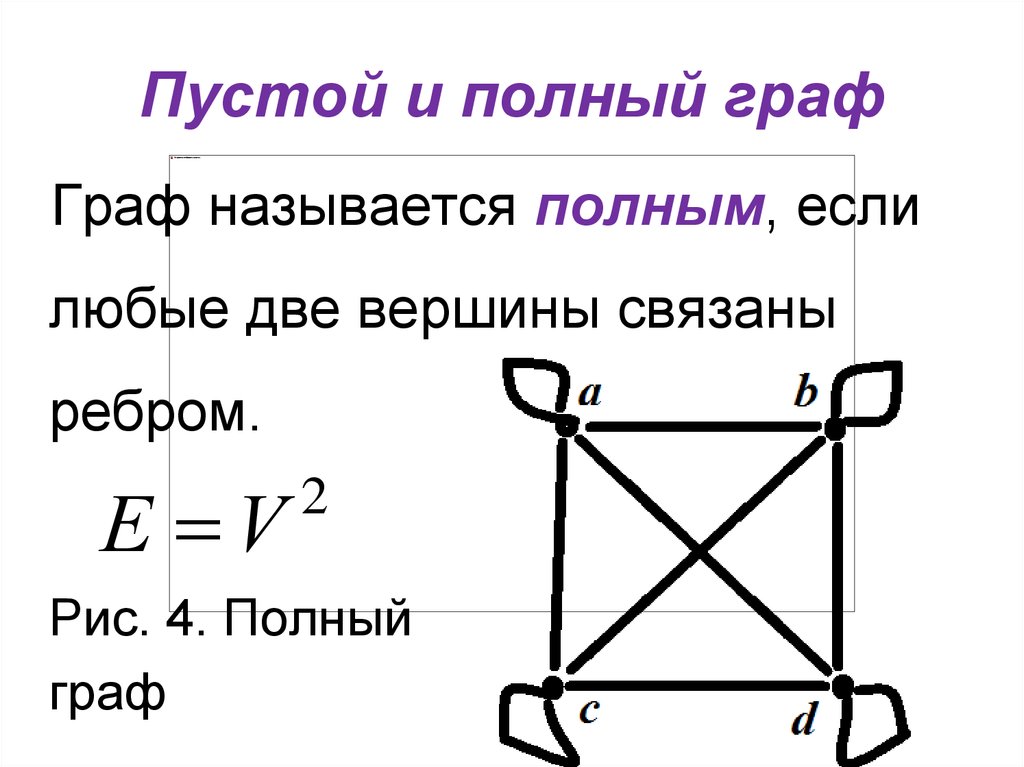
Граф называется полным, если
любые две вершины связаны
ребром.
E V
2
Рис. 4. Полный
граф

8. Двудольный граф граф

Граф называется двудольным если
множество его ребер разбито на два
подмножества,
V V1 V2 , V1 V Ø
и ребрами связаны только вершины
из разных подмножеств.

9. Двудольный граф граф

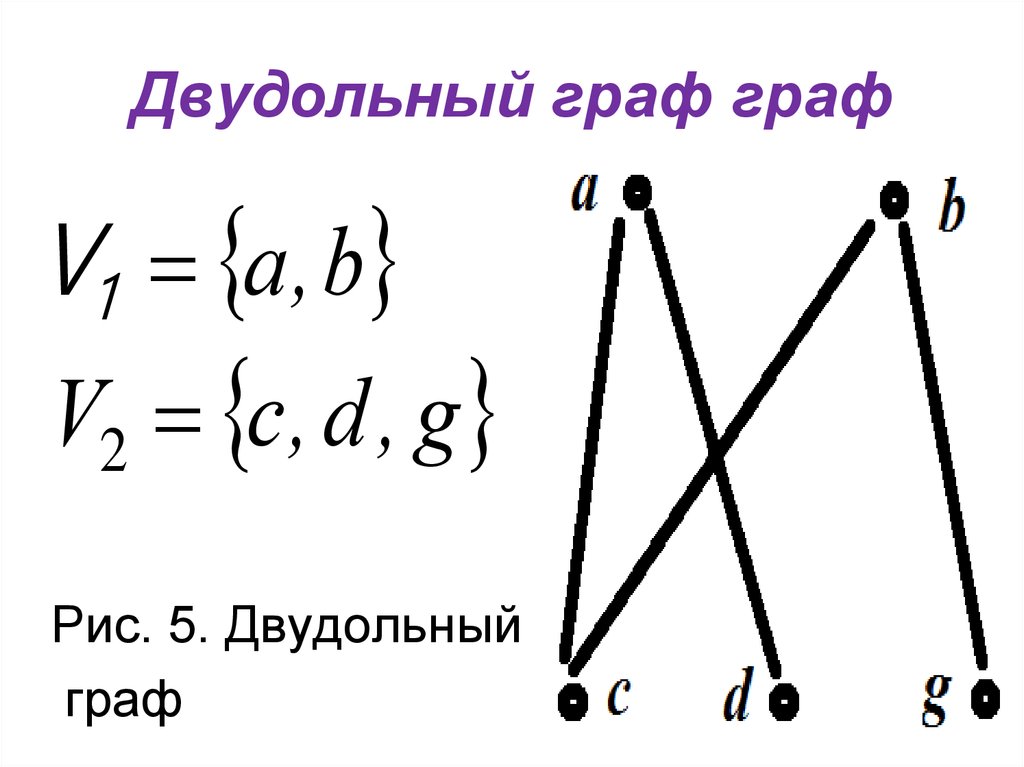
V1 a , b
V2 c , d , g
Рис. 5. Двудольный
граф

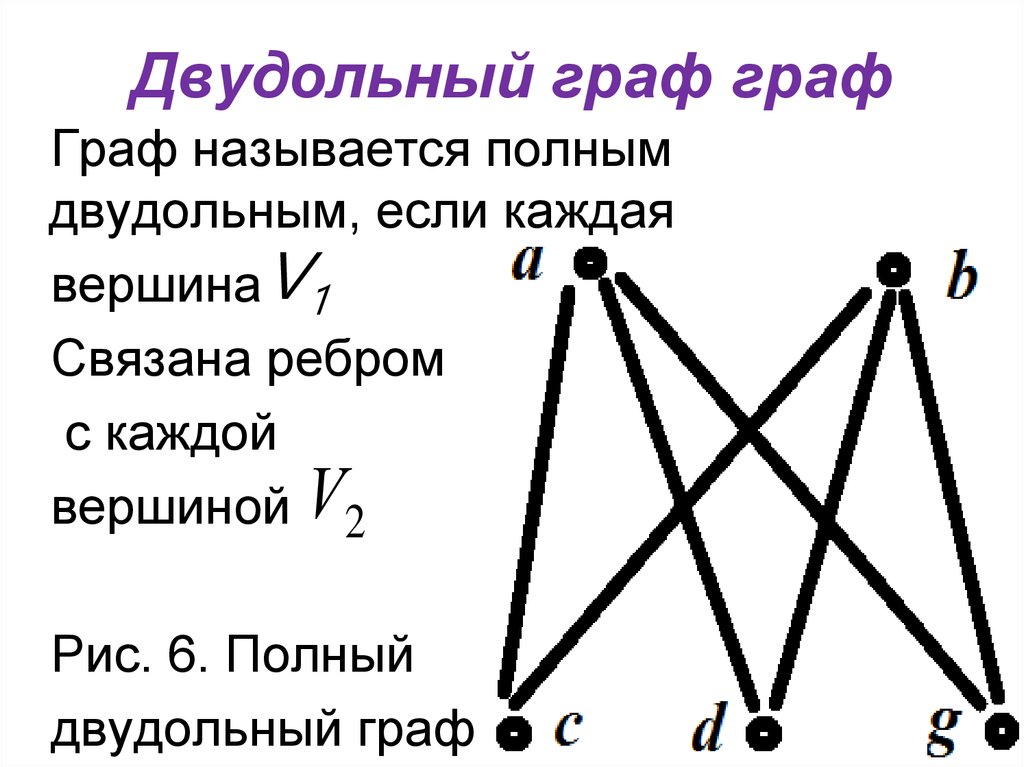
10. Двудольный граф граф

Граф называется полным
двудольным, если каждая
вершинаV1
Связана ребром
с каждой
вершиной V2
Рис. 6. Полный
двудольный граф

11. Двудольный граф граф

Если
V1 n1 , а V2 n2
полный двудольный граф
обозначается:
K n1 ,n2
, то

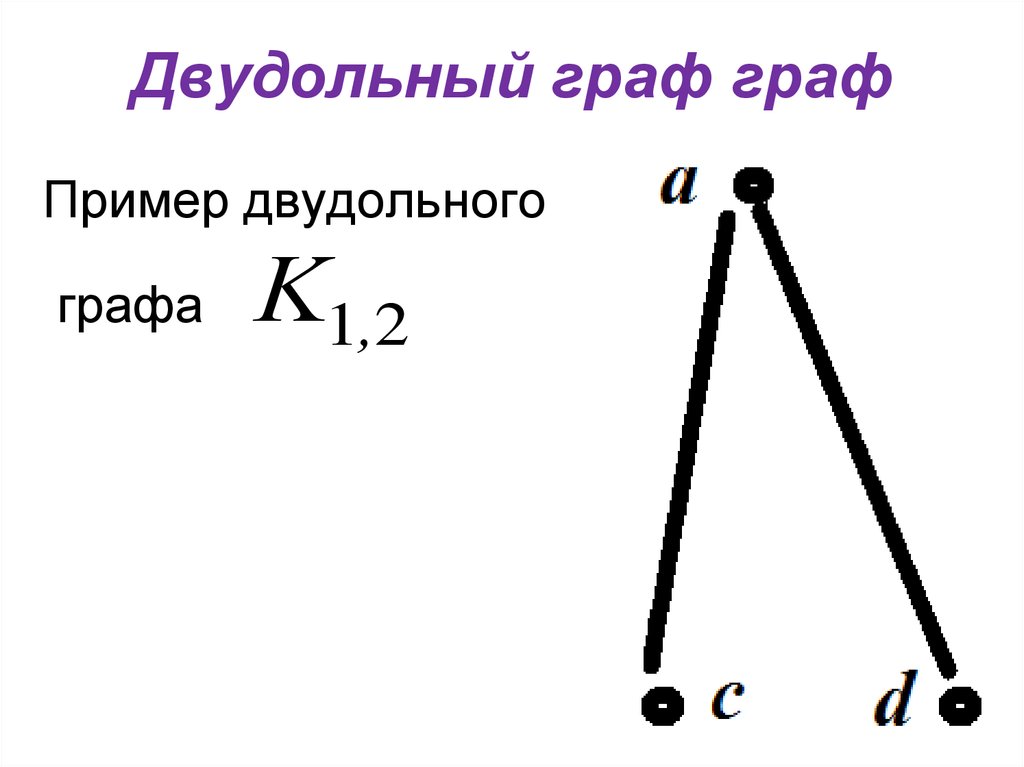
12. Двудольный граф граф

Пример двудольного
графа
K1,2

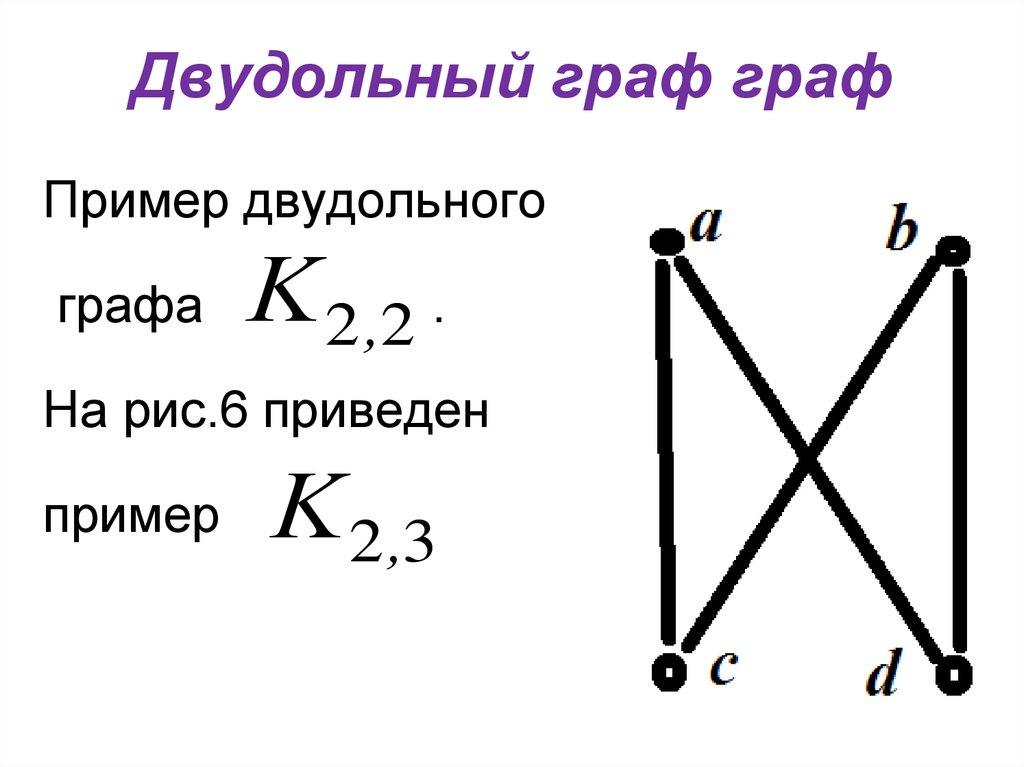
13. Двудольный граф граф

Пример двудольного
графа
K 2,2 .
На рис.6 приведен
пример
K 2,3