Аксиома параллельных прямых

1.

Аксиома
параллельных прямых

2.

– На чём основаны доказательства самых первых теорем?
– Доказательства самых первых теорем основаны на аксиомах.
Аксиома (от греч. «аксиос» – ценный, достойный) –
это утверждение, устанавливающее некоторое свойство
и принимаемое без доказательства.
Аксиомы возникли из опыта, они являются наглядно
очевидными и не вызывают сомнений.

3.

Через любые две точки проходит прямая и
при том только одна.
В
А

4.

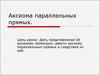
На любом луче от его начала можно
отложить отрезок, равный данному, и
притом только один.
О
А
h

5.

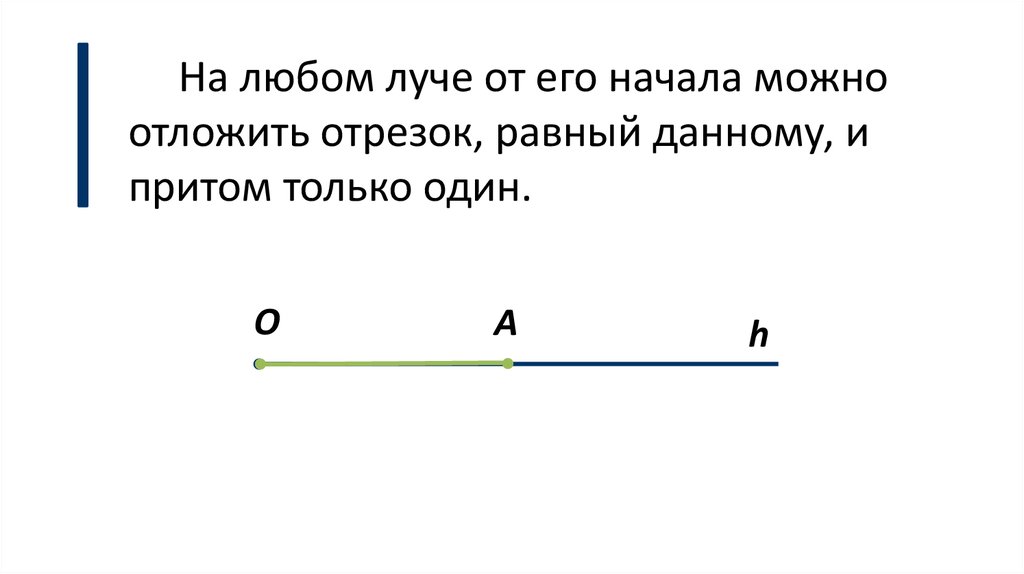
От любого луча в заданную сторону
можно отложить угол, равный данному
неразвёрнутому углу, и притом только
один.
В
О
h
А

6.

O
b
a
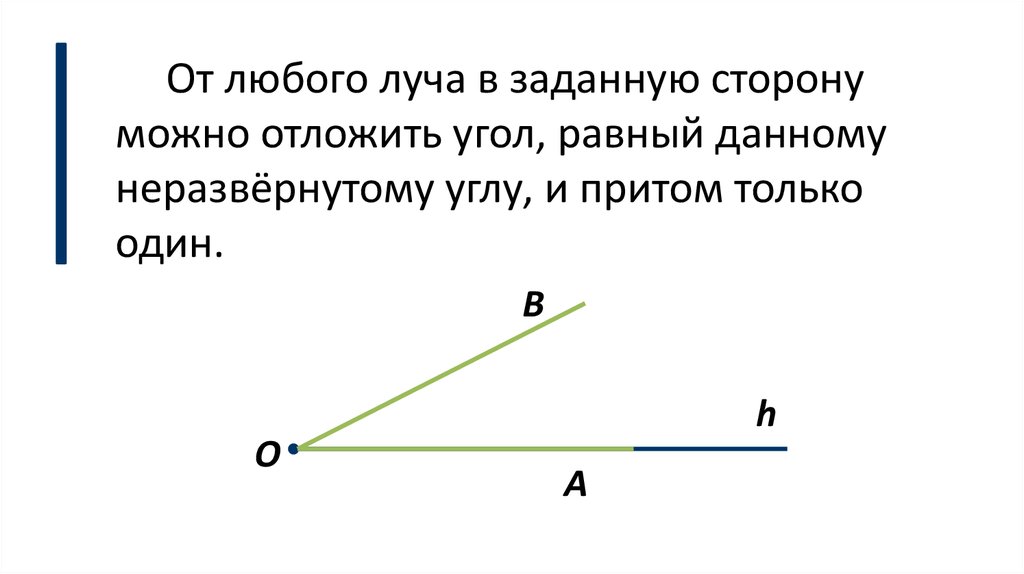
a ⊥ c,
c
b ⊥ c,
значит, а || b.
– Можно ли провести ещё одну прямую через точку О,
параллельную прямой а?

7.

Аксиома параллельных прямых
Через точку, не лежащую на данной
прямой, проходит только одна прямая,
параллельная данной.

8.

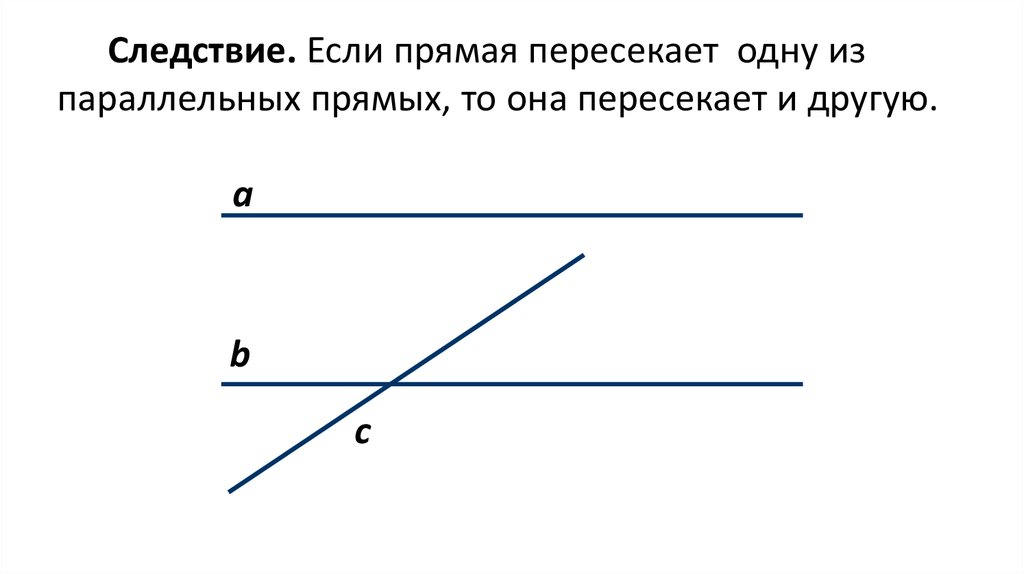
Следствие. Если прямая пересекает одну из
параллельных прямых, то она пересекает и другую.
a
b
c

9.

Следствие. Если две прямые параллельны третьей,
то они параллельны.
a
b
c
а || b

10.

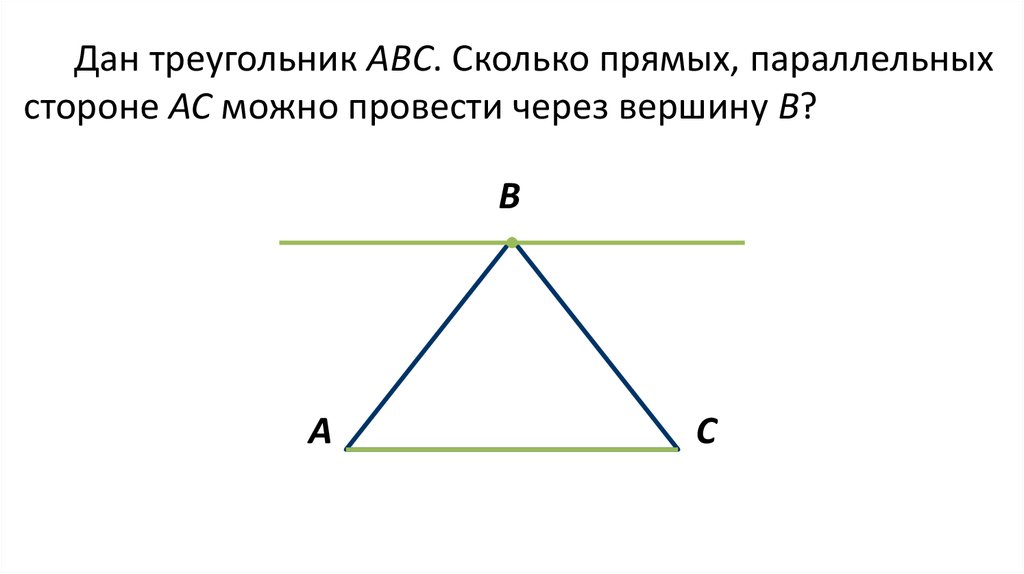
Дан треугольник АВС. Сколько прямых, параллельных
стороне АС можно провести через вершину В?
В
А
С

11.

Евклидова геометрия
Аксиомы
Рассуждения
Новые утверждения
Евклид ( 3 в до н. э.)

12.

Геометрия Лобачевского
Через точку, не лежащую
на данной прямой,
проходит более чем одна
прямая, параллельная
данной.
Н. И. Лобачевский (1792 – 1856)

13.

Геометрия Лобачевского точнее
описывает геометрию Вселенной, чем
геометрия Евклида.