Решение минимаксной обобщенной задачи о назначениях при неодновременном поступлении работ. (Лекция 4)

1.

Решение минимаксной обобщенной задачи о назначениях
при неодновременном поступлении работ
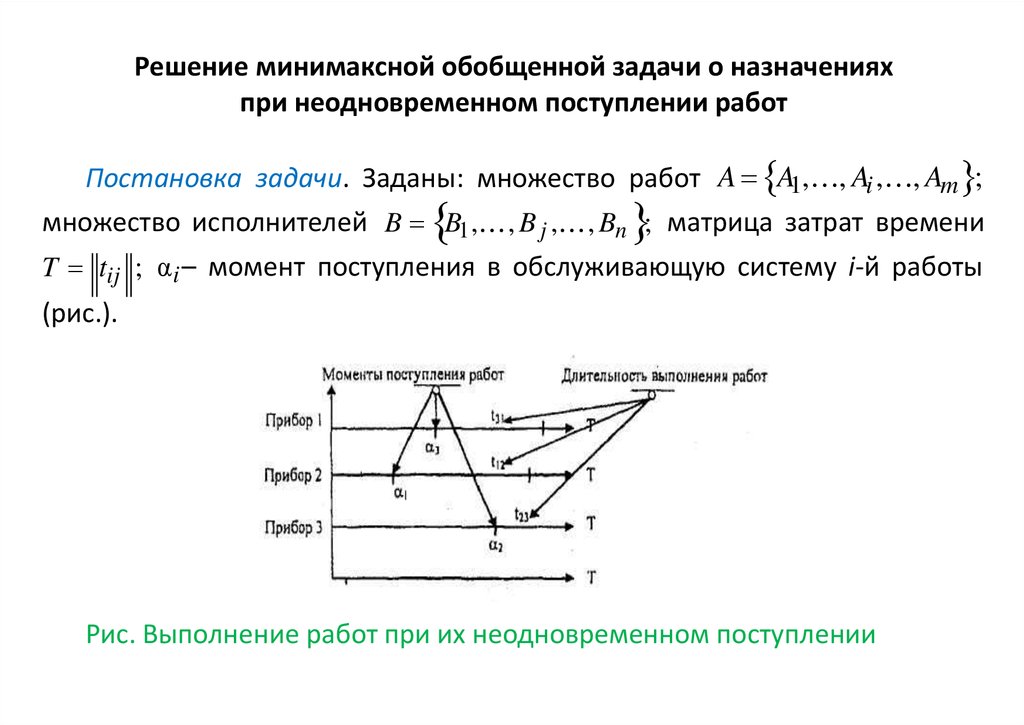
Постановка задачи. Заданы: множество работ A A1, , Ai , , Am ;
множество исполнителей B B1 , , B j , , Bn ; матрица затрат времени
T tij ; αi – момент поступления в обслуживающую систему i-й работы
(рис.).
Рис. Выполнение работ при их неодновременном поступлении

2.

При распределении работ по приборам и расчете загрузки приборов
необходимо придерживаться следующих принципов:
– порядок выполнения работ
на приборах должен обеспечивать
уменьшение времени их простоя, т.е. в первую очередь должны быть
распределены работы, имеющие минимальное значение αi -е моментов
их поступления в систему;
– при расчете загрузки прибора необходимо учитывать его простой,
вызванный ожиданием поступления следующей работы.

3.

Вариант 1. Отсутствие простоя j-гo прибора (рис.), т.к. момент
поступления ik -й работы αik меньше момента окончания выполнения
предыдущей z–1 -й по порядку работы, αi k T j Gvz 1 .
Вариант 2: простой j-го прибора существует, т.к. момент поступления z-й
по порядку работы, имеющий номер ik , больше момента окончания
предыдущей по порядку z–1-й работы, т.е. αi T j Gvz 1 (рис.)
k

4.

Алгоритм решения: предварительный этап и три основных этапа.
Предварительный этап. Все работы упорядочиваются в порядке
возрастания моментов их поступления в обслуживающую систему, т.е.
αi1 αiл αim .
Строки матрицы T tij ; также упорядочиваются: T tik j , k 1, m.
Этап.1. Формируется множество всех возможных вариантов
распределения работ по исполнителям, и находится нижняя оценка
ξ G0 max 1, 2
m
1
1 : τik min tik j , 1 max ik αik , k 1, m; 2 αi1 ik .
n
j
k 1
Этап 2. Распределяется первая работа, имеющая индекс i1 т.е. z i1.
Шаг 2.1. Исходное множество делится на n непересекающихся
подмножеств G11 , ,G1v , ,G1n : (рис.).

5.

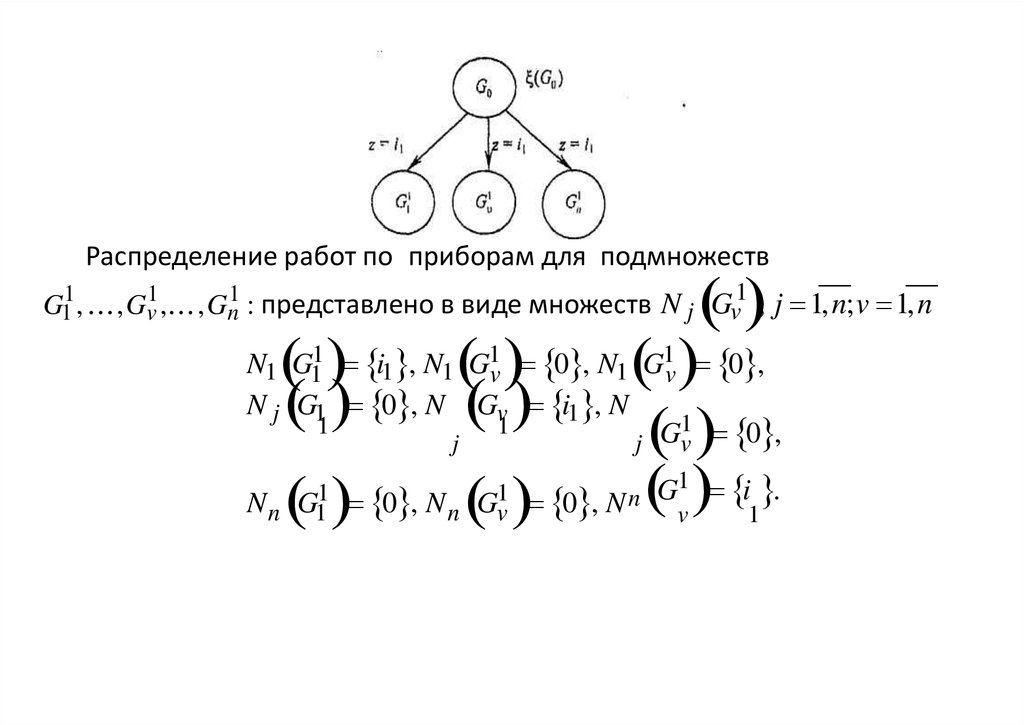
Распределение работ по приборам для подмножеств
1
G11 , ,Gv1 , ,Gn1 : представлено в виде множеств N j Gv , j 1,n;v 1,n
1 i .
G
1
1
n
N n G1 0 , N n Gv 0 , N
v
1
N1 G11 i1 , N1 G1v 0 , N1 G1v 0 ,
N j G1 0 , N Gv i1 , N
1 0 ,
1
1
G
j
j
v

6.

Шаг 2.2. Для каждого из вновь образованных подмножеств находятся
три частные оценки 1 , 2 , 3 . Окончательно, ξ G1v max 1, 2 , 3 ,
1 max i αi , k 2, m; T j G1v ti j +αi , ik N j G1v ,
k
k
k
k
m
1 n
T j1 T j2 T jn ; 3 T jn ; 2 T js ik .
n s 1
k 2
Таким образом, на этапе 2 для каждого из подмножеств определена
нижняя оценка.
Этап 3. Конкурирующими являются подмножества, полученные на
этапе 2, и в качестве перспективного выбирается подмножество,
имеющее минимальную оценку. Предположим, что это подмножество –
Gv1. В качестве второй по порядку рассматривается работа i2 . Она
назначается первому, второму, ..., v-му, ..., n-му исполнителям. В
1 , ,G1
1
,
,G
результате образуются новые подмножества G v,1
v,v
v,n (рис.).

7.

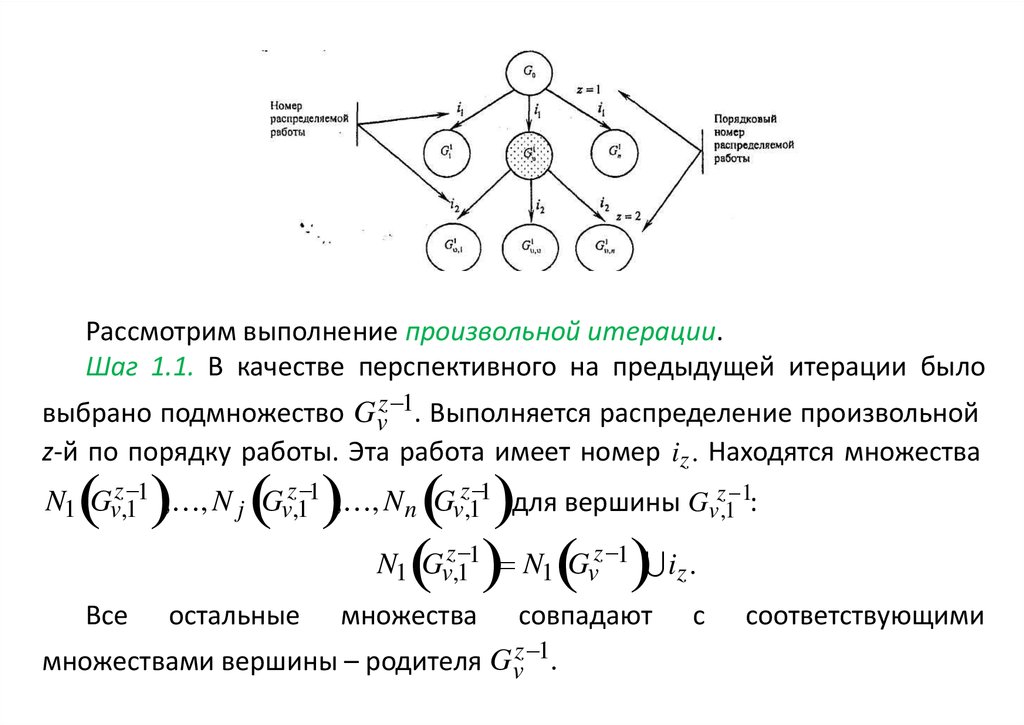
Рассмотрим выполнение произвольной итерации.
Шаг 1.1. В качестве перспективного на предыдущей итерации было
выбрано подмножество Gvz 1. Выполняется распределение произвольной
z-й по порядку работы. Эта работа имеет номер iz . Находятся множества
z 1
z 1
N1 Gv,1
N
G
1 v iz .
1 , , N G z 1 , , N G z 1 для вершины G z 1:
N1 Gvz
,1
j
v,1
n v,1
v,1
Все
остальные
множества
совпадают
множествами вершины – родителя G vz 1.
с
соответствующими

8.

Шаг 1.2. Для каждого из подмножеств рассчитываются три частные
оценки, и в качестве нижней оценки выбирается максимальная из них:
ξ G1v,v max 1, 2 , 3 ; 1: τ ik min tik j , 1 max τ ik αik ,k z 1, m.
j
Для 2 и 3 определяется занятость j-го прибора:
1
1
Tj
Gvz ,v bi j , ik N j Gvz , v .
k
Введение переменной bik j предназначено для учета возможности
простоя j-го прибора:
bik j tik j в случае отсутствия простоя прибора.

9.

bik j αik tik j T j Gvz 1 при наличии простоя j-го прибора.
Полученные
значения T j упорядочиваются в
последовательности: T j1 T j2 T jn . Окончательно
m
1 r
3 T jn ; 2 T js i
k
r s 1
k z 1
возрастающей
если z m n,
n,
, r m z, если z m n.
Таким образом, определены нижние оценки для всех конкурирующих
подмножеств.

10.

В качестве перспективного выбирается подмножество с минимальной
нижней оценкой. Итерации продолжаются до тех пор, пока в качестве
последней распределяемой работы не будет выбрана последняя по
порядку работа с номером im . Для подмножеств, образованных в
результате распределения последней im -й работы, значение критерия
совпадает с нижней оценкой.

11.

Распределение файлов по уровням памяти ВС методом ветвей и границ
Постановка задачи. Задана вычислительная система, содержащая М
типов памяти, каждый из которых характеризуется значением объема и
временными параметрами доступа к данным. Необходимо отметить, что
лучшие временные характеристики имеют типы памяти, относящиеся к
верхним уровням иерархии (рис.), в то же время эти типы памяти
характеризуются меньшими объемами.
Рис. Иерархия типов памяти

12.

Для каждого из типов памяти определены значения объемов
Vi , i 1, M и времени доступа к данным ti , i 1, M . В вычислительной
системе необходимо хранить N информационных файлов/массивов для
каждого из которых установлены следующие параметры: rj активность jго файла; W j объем j-го файла; j 1, N. Под активностью rj понимается
количество обращений к j-му файлу за период функционирования
системы. Необходимо распределить файлы по уровням памяти таким
образом, чтобы суммарное время, затрачиваемое на доступ к ним за
период функционирования системы, было бы минимальным и
выполнялись ограничения на объемы для каждого из типов памяти.
Очевидным является выполнение ограничения целостности файлов:
каждый файл размещается только на одном уровне иерархии памяти.
Вводится переменная x j , j 1, N , где x j i если j-й файл
распределен на i-й уровень памяти.
Необходимо найти вектор решений x x1, x2 , , x j , , xN .

13.

В частности вектор x 1,1, ,1, ,1 ответствует распределению всех
файлов на первый уровень иерархии памяти.
Критерий. Минимизация суммарных затрат на доступ к каждому из
файлов за время функционирование системы.
Очевидно, что затраты на доступ к j-му файлу равны количеству
обращений к нему за время функционирования системы, умноженному
на время одного доступа, т.е. r j ti .
Критерий представляется в виде:
N
M
0, если a 0;
F r j ti (1 δ(i x j )) min, δ(a)
1, если a 0.
j 1 i 1
Ограничения. Суммарный объем всех файлов, размещаемых на i-м
уровне, должен быть меньше либо равен объему памяти i-го уровня.
Количество ограничений равно количеству уровней:
N
W j (1 δ(i x j )) Vi , i 1, M .
j 1

14.

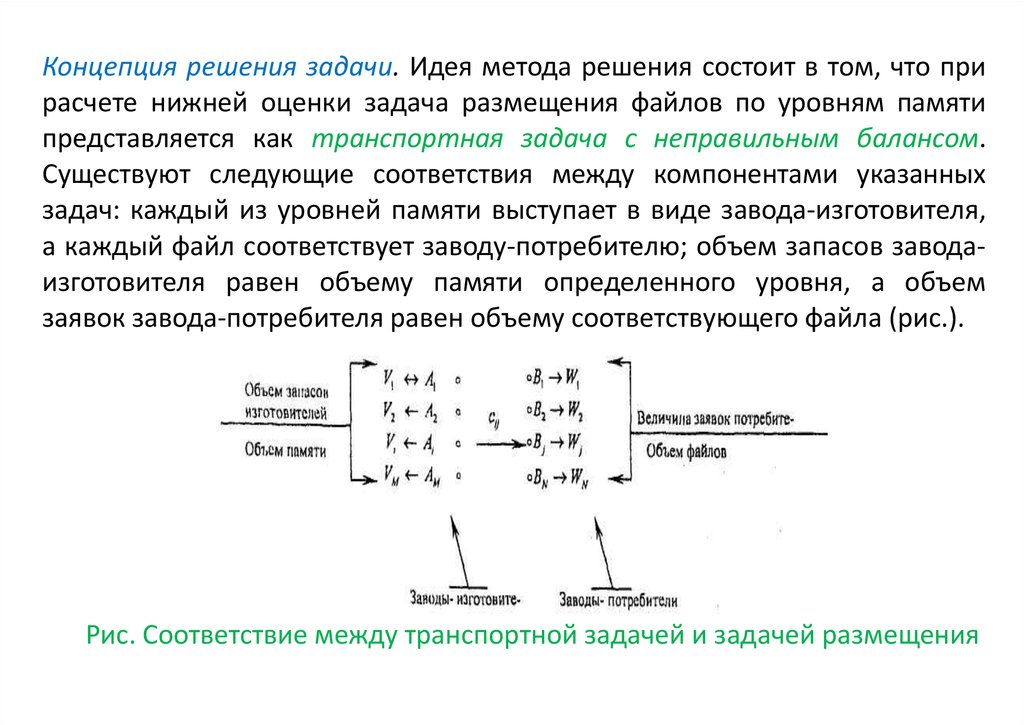
Концепция решения задачи. Идея метода решения состоит в том, что при
расчете нижней оценки задача размещения файлов по уровням памяти
представляется как транспортная задача с неправильным балансом.
Существуют следующие соответствия между компонентами указанных
задач: каждый из уровней памяти выступает в виде завода-изготовителя,
а каждый файл соответствует заводу-потребителю; объем запасов заводаизготовителя равен объему памяти определенного уровня, а объем
заявок завода-потребителя равен объему соответствующего файла (рис.).
Рис. Соответствие между транспортной задачей и задачей размещения

15.

В транспортной задаче задана стоимость cij перевозки единицы
продукции из Ai -го завода изготовителя в Bj-й завод-потребитель. Для
задачи размещения аналогично определяются затраты времени на
rj
передачу единицы объема файла: cij
ti .
Wj
Транспортной задаче соответствует транспортная таблица.
Предварительный этап. На этом этапе по исходным данным
формируется транспортная таблица следующего вида (табл.1). Строки
соответствуют уровням памяти, столбцы – файлам.
Элементы транспортной таблицы cij представляют временные затраты
на считывание единицы j-го файла с i-го уровня памяти за период
функционирования системы. Тогда r j ti .– суммарные затраты времени,
необходимые для выполнения rj обращений к j-му файлу за период
rj
функционирования, a Wj – объем j-го файла: cij
t.
Wj i

16.

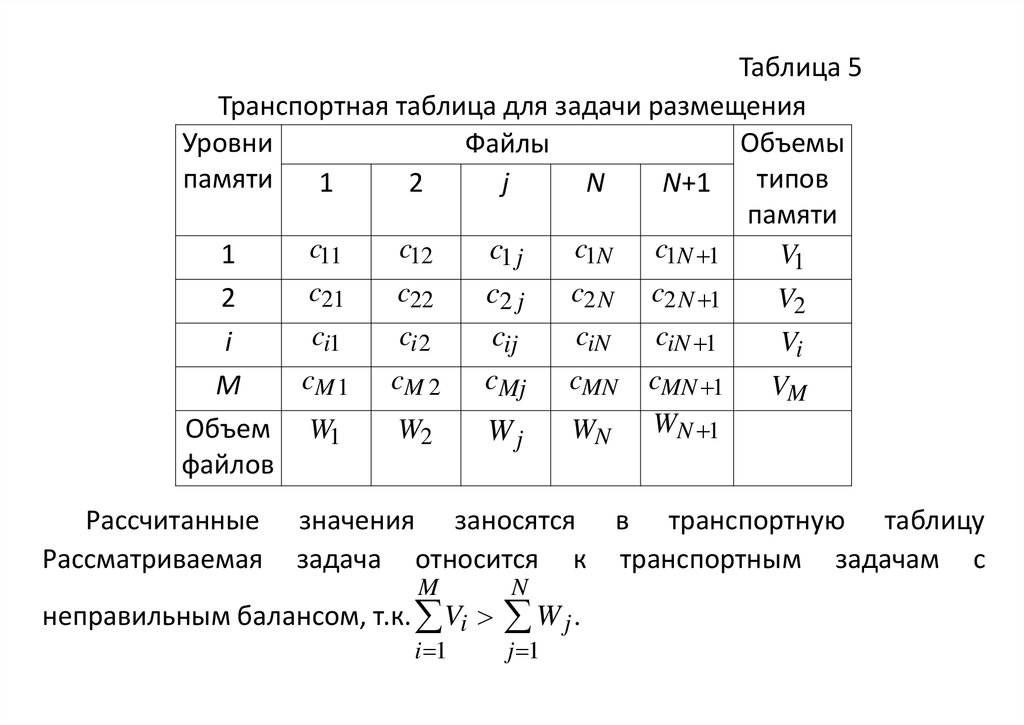
Таблица 5
Транспортная таблица для задачи размещения
Уровни
Объемы
Файлы
памяти
типов
1
2
j
N
N+1
памяти
c11
c12
c1N c1N 1
c1 j
1
V1
c21
c22
c2N c2N 1
c2 j
2
V2
ci1
ci2
ciN
ciN 1
cij
i
Vi
cM1 cM 2
cMj cMN cMN 1
M
VM
Объем W1
W2
WN WN 1
Wj
файлов
Рассчитанные
Рассматриваемая
значения заносятся в транспортную таблицу
задача относится к транспортным задачам с
M
Wj.
i 1
j 1
неправильным балансом, т.к. Vi
N

17.

Для приведения полученной транспортной задачи к задаче с
правильным балансом вводится фиктивный файл с номером N+1 и
объемом равным
M
N
i 1
j 1
WN 1 Vi W j .
Элементы матрицы ciN 1 0 , т.е. затраты на считывание фиктивного
N+1-го файла равны нулю. Эти значения заносятся в дополнительный
столбец. После этого выполняется следующая итерация.
Итерация 0
Этап 1. Формируется начальное множество Go, представляющее
собой множество возможных вариантов размещения файлов по уровням
памяти:
все массивы размещаются на первом уровне памяти x 1,1, ,1 ;
первый, второй, ..., N-1-й массивы размещаются на первом уровне
памяти, N-й файл – на втором уровне памяти x 1,1, ,2 ;
все массивы размещаются на М-м уровне памяти x M , M , , M .

18.

Для множества Go находится нижняя оценка ξ Go . В качестве нижней
оценки используется значение критерия суммарных затрат, получаемое
при решении транспортной задачи. Перед решением транспортной
задачи целесообразно столбцы упорядочить в порядке убывания
rj
r j1
r j2
отношения:
N , а строки – в порядке возрастания
W j1 W j2
W jN
значений времени считывания данных: ti1 ti2 tiM . Тогда
допустимое решение транспортной задачи, полученное методом северозападного угла, является также и оптимальным решением. В том случае,
если упорядочивание столбцов и строк по значениям r j W j и ti не
производится, то после получения допустимого решения для нахождения
оптимального варианта может использоваться, либо распределительный
метод, либо метод потенциалов. При решении транспортной задачи на
концептуальном уровне допускается размещение одного файла на
нескольких уровнях. Следовательно, значение критерия для исходной
задачи не может быть меньше, чем значение нижней оценки, полученной

19.

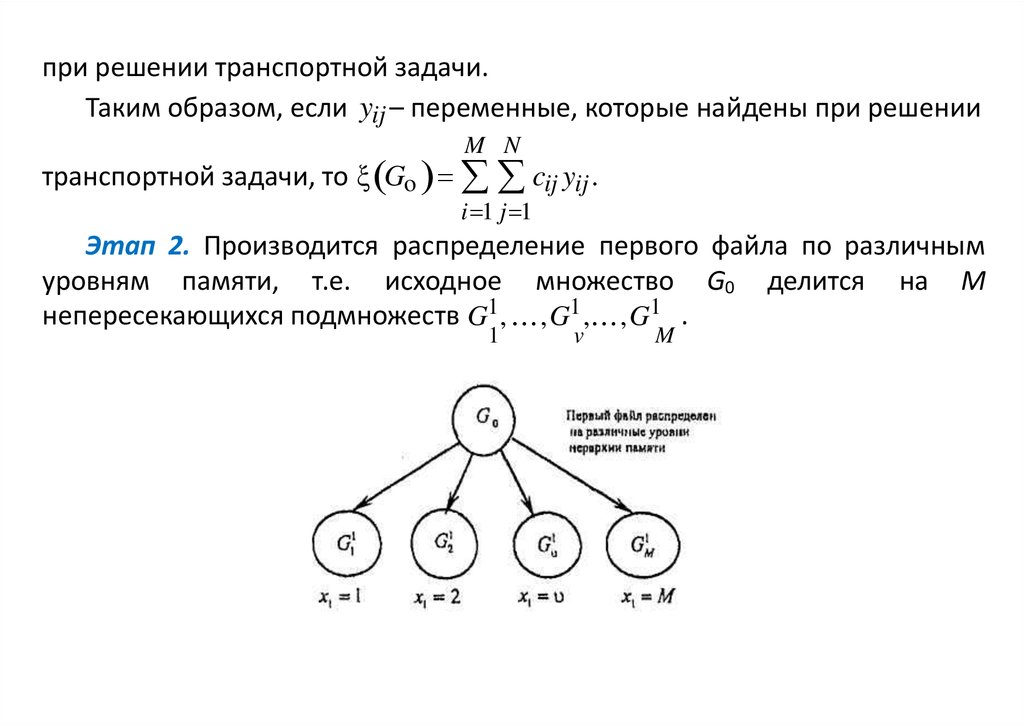
при решении транспортной задачи.
Таким образом, если yij – переменные, которые найдены при решении
M N
транспортной задачи, то ξ Go cij yij .
i 1 j 1
Этап 2. Производится распределение первого файла по различным
уровням памяти, т.е. исходное множество G0 делится на М
непересекающихся подмножеств G1 , ,G1 , ,G1 .
1
v
M

20.

Нижняя оценка ξ G1 подмножества G1 определяется как:
ξ G11 T G11 H G11 ,
где T G11 – компонента, учитывающая временные затраты на считывание
первого файла с первого уровня памяти. Определение этой компоненты
базируется на том, что известно, на каком уровне памяти будет размещен
Компонента H G11 находится из решения транспортной задачи. Для
первый файл: T G11 r1 t1.
этого вначале выполняются необходимые преобразования для
транспортной таблицы, соответствующие множеству
G11. Эти
преобразования учитывают, что первый файл распределен и занята часть
объема памяти первого типа. Тогда из транспортной таблицы,
соответствующей множеству Go, вычеркивается первый столбец и
корректируется значение объема для первого типа памяти (рис.).

21.

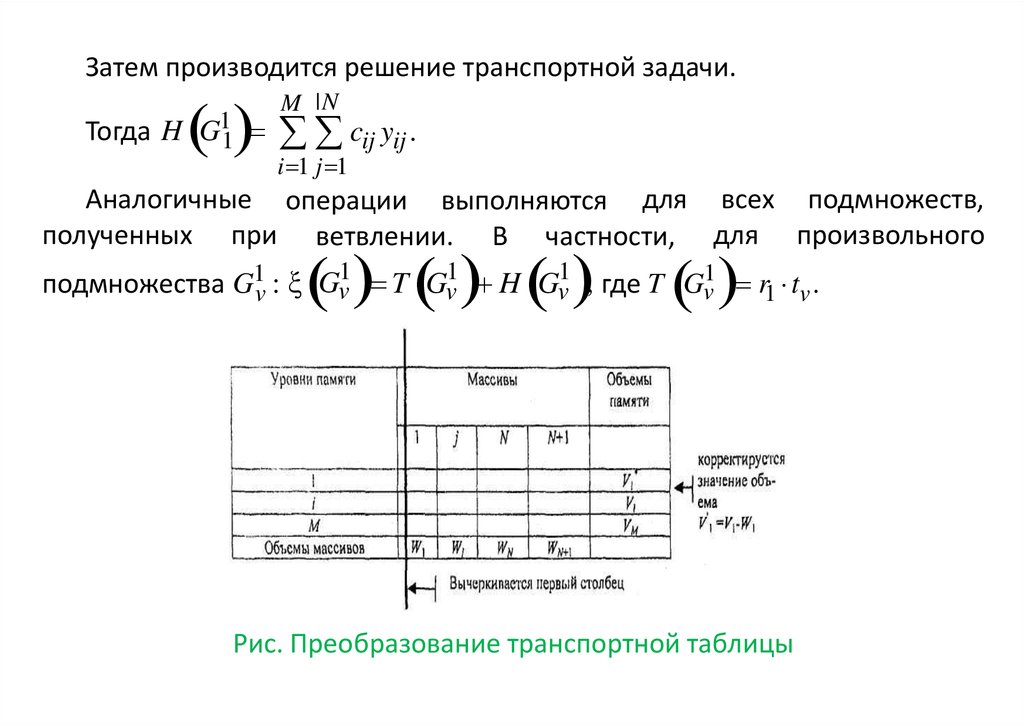
Затем производится решение транспортной задачи.
Тогда H G11
M |N
cij yij .
i 1 j 1
Аналогичные операции выполняются для всех подмножеств,
полученных при ветвлении. В частности, для произвольного
подмножества G1v : ξ Gv1 T Gv1 H Gv1 , где T Gv1 r1 tv .
Рис. Преобразование транспортной таблицы

22.

Для вычисления компоненты
H Gv1
необходимо
выполнить
преобразования транспортной таблицы множества родителя Go. Для этого
в транспортной таблице, соответствующей множеству-родителю Go,
вычеркивается первый столбец и корректируется значение объема памяти
для v-го уровня, т.е. находится скорректированное значение Vv:
Vv Vv W1.
Для полученной транспортной таблицы находится оптимальное
решение, и найденное значение критерия транспортной задачи
представляет собой вторую компоненту нижней оценки:
H Gv1
M |N
cij yij .
i 1 j 1
Таким образом, после выполнения второго этапа для каждого из
конкурирующих подмножеств известна нижняя оценка и найдена
соответствующая транспортная таблица, которая должна сохраняться для
последующих преобразований.

23.

Этап 3. В качестве перспективного из числа конкурирующих
выбирается подмножество, имеющее минимальную нижнюю оценку, и
производится переход к выполнению следующей итерации.
Итерация 1. На предыдущей итерации в качестве перспективного
было выбрано подмножество G1v.
Этап 1. Производится распределение второго файла, т.е.
подмножество G1v делится на М непересекающихся подмножеств (рис.).
Подмножество G1v,1 представляет собой все те варианты размещения
файлов по уровням памяти, в которых первый файл распределен на v-й
уровень, а второй файл – на первый уровень памяти. Распределение
других файлов по уровням памяти еще не произведено.
Для образованных подмножеств находится нижняя оценка. В
частности,
для
подмножества
T G1v,1 r1 tv r2 t1.
1
Gv,1
:
1
1
1
T Gv,1
H Gv,1
,
ξ Gv,1

24.

Для нахождения
компоненты
необходимо
выполнить
соответствующей
множеству-
H G1v,1
изменения в транспортной таблице,
родителю G1v.
Замечание. В транспортной таблице, относящейся к подмножеству G1v,
был вычеркнут первый столбец, и скорректировано значение объема v -го
уровня памяти. Дополнительные преобразования этой таблицы состоят в
том, что вычеркивается второй столбец и корректируется значение
объема памяти для первого уровня: V1 V1 W2 .
После этого решается транспортная задача и вычисляется значение
M |N
критерия: H G1v,1 cij yij .
i 1 j 1
Замечание. Перед вычислением нижних оценок для подмножеств
вначале необходимо проверить допустимость соответствующего варианта
распределения. В том случае, когда объем памяти уровня меньше, чем
объем файлов, назначаемых на этот уровень, то, очевидно, такой вариант

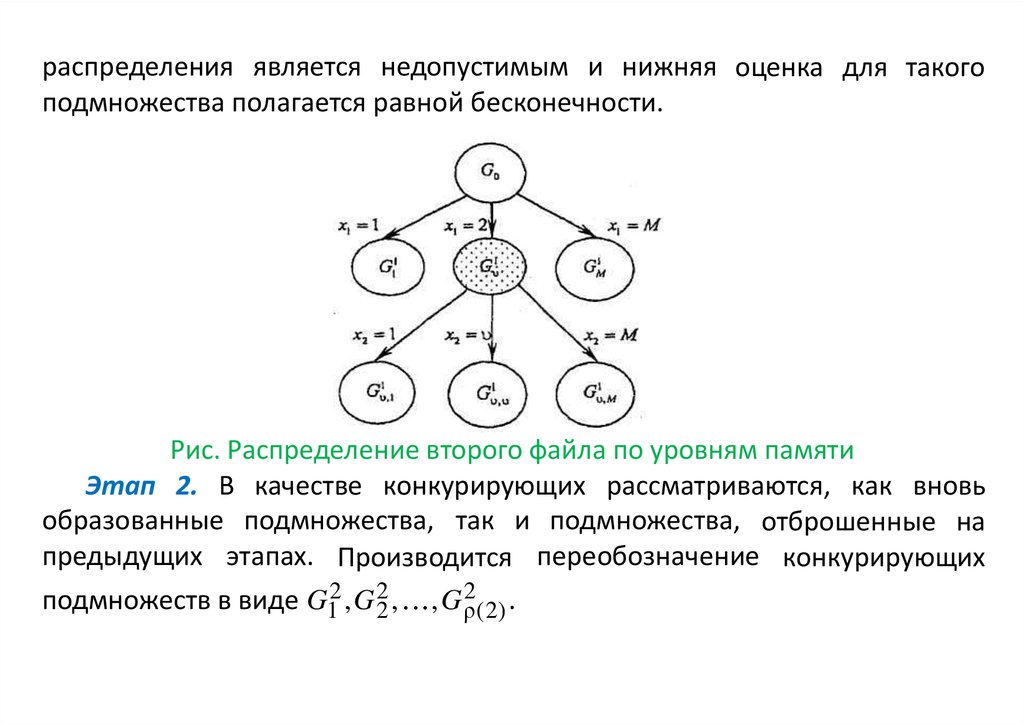
25.

распределения является недопустимым и нижняя оценка для такого
подмножества полагается равной бесконечности.
Рис. Распределение второго файла по уровням памяти
Этап 2. В качестве конкурирующих рассматриваются, как вновь
образованные подмножества, так и подмножества, отброшенные на
предыдущих этапах. Производится переобозначение конкурирующих
2 .
подмножеств в виде G12 ,G 22 , ,G ρ(2)

26.

В качестве перспективного выбирается подмножество, имеющее
минимальную нижнюю оценку. Процесс ветвления продолжается до тех
пор, пока не будут распределены все массивы. Очевидно, что на
последнем этапе при распределении N-гo файла, нижняя оценка будет
критерия совпадает с нижней оценкой ξ GvN .
состоять только из одной составляющей T G Nv . В этом случае значение
Замечание.
Для
анализируемой
задачи
существует
модифицированный вариант ветвления, когда в качестве конкурирующих
рассматриваются только вновь образованные подмножества. Такая
процедура повторяется до тех пор, пока не будет распределен последний
файл, т.е. будут получены оценки для конечных подмножеств и среди них
выбрано подмножество с минимальной оценкой. Полученное
минимальное значение объявляется текущим рекордом. После этого
анализируется
необходимостьветвления
ранее
отброшенных
подмножеств.

27.

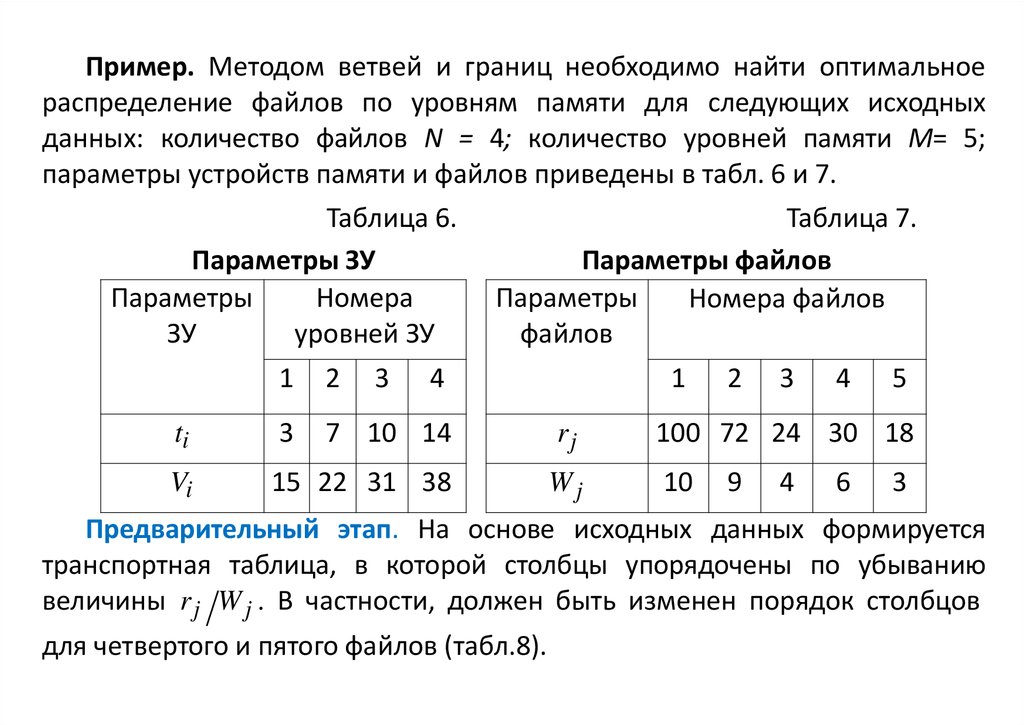
Пример. Методом ветвей и границ необходимо найти оптимальное
распределение файлов по уровням памяти для следующих исходных
данных: количество файлов N = 4; количество уровней памяти M= 5;
параметры устройств памяти и файлов приведены в табл. 6 и 7.
Таблица 6.
Таблица 7.
Параметры ЗУ
Параметры файлов
Параметры
Номера
Параметры
Номера файлов
ЗУ
уровней ЗУ
файлов
1
2
3
4
1
ti
3
7 10 14
rj
Vi
15 22 31 38
Wj
2
3
4
5
100 72 24 30 18
10
9
4
6
3
Предварительный этап. На основе исходных данных формируется
транспортная таблица, в которой столбцы упорядочены по убыванию
величины r j W j . В частности, должен быть изменен порядок столбцов
для четвертого и пятого файлов (табл.8).

28.

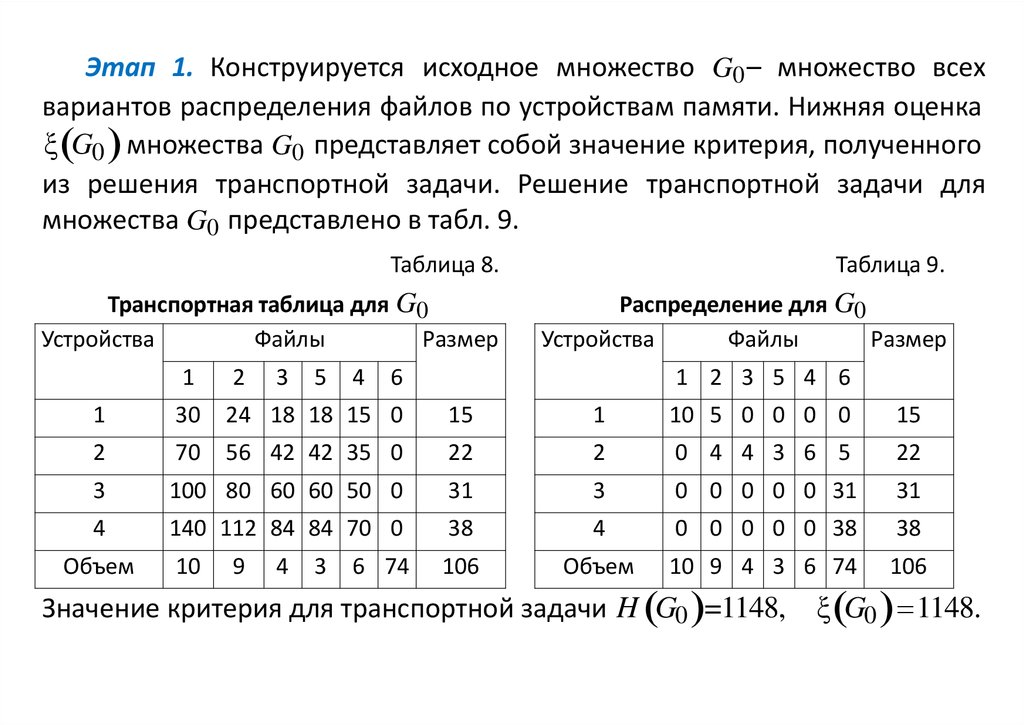
Этап 1. Конструируется исходное множество G0 – множество всех
вариантов распределения файлов по устройствам памяти. Нижняя оценка
ξ G0 множества G0 представляет собой значение критерия, полученного
из решения транспортной задачи. Решение транспортной задачи для
множества G0 представлено в табл. 9.
Таблица 8.
Таблица 9.
Транспортная таблица для G0
Устройства
Файлы
Размер
Распределение для G0
Устройства
Файлы
Размер
1
2
1
30
24 18 18 15 0
15
1
10 5 0 0 0 0
15
2
70
56 42 42 35 0
22
2
0 4 4 3 6 5
22
3
100 80 60 60 50 0
31
3
0 0 0 0 0 31
31
4
140 112 84 84 70 0
38
4
0 0 0 0 0 38
38
10
106
Объем
10 9 4 3 6 74
106
Объем
9
3
4
5
3
4
6
6 74
1 2 3 5 4 6
Значение критерия для транспортной задачи H G0 =1148,
ξ G0 1148.

29.

Этап 2. Производится распределение первого файла на различные
устройства памяти, Для этого подмножество G0 разбивается на четыре
непересекающихся подмножества: G11 ,G12 ,G31 и G14 (рис.). Подмножество
G11 содержит все те варианты, в которых первый файл распределен на
первое устройство памяти, подмножество G12 – все те варианты, в которых
первый файл распределен на второе устройство и т.д. Последовательно
находятся нижние оценки для сформированных подмножеств.
Для
G11 :
ξ G11 T G11 H G11 ; T G11 r1 t1 100 3 300; H G11
значение критерия для транспортной таблицы, в которой исключен
первый столбец и скорректировано значение для свободного объема
памяти первого устройства (табл. 10). Решение транспортной задачи для
подмножества G11 приведено в табл. 11.
Значение
критерия
для
транспортной
задачи:
H G11 848.
Окончательно, ξ G11 1148. Аналогично находятся нижние оценки для

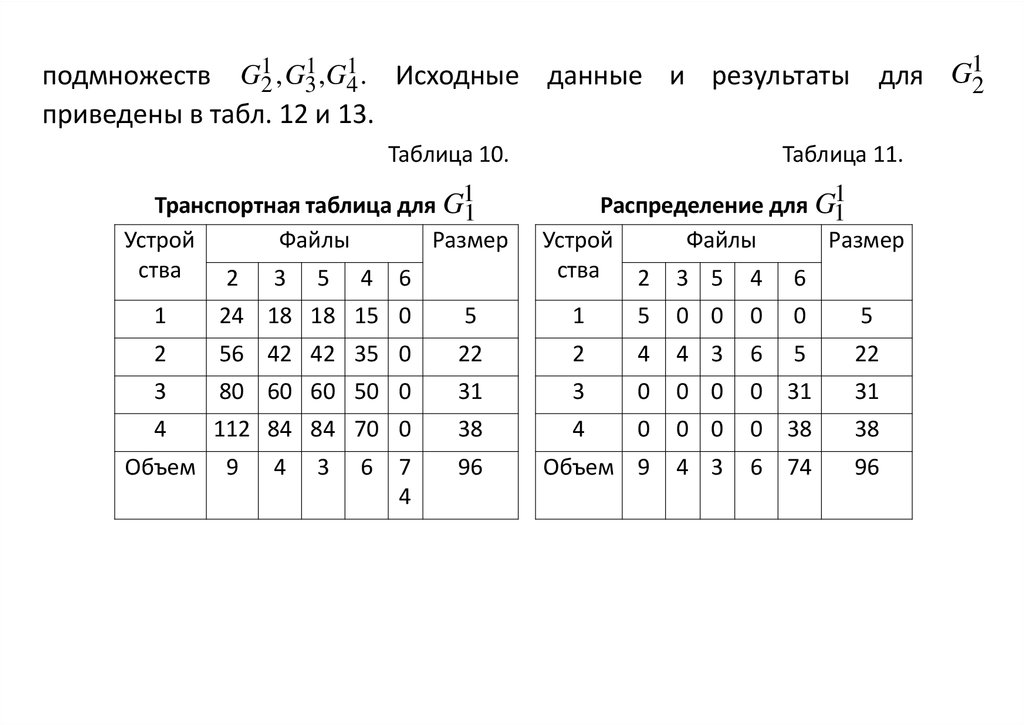
30.

подмножеств G21 ,G31 ,G14 . Исходные данные и результаты для G12
приведены в табл. 12 и 13.
Таблица 10.
Таблица 11.
Транспортная таблица для G11
Устрой
Файлы
Размер
ства
2 3 5 4 6
Распределение для G11
Устрой
Файлы
Размер
ства
2 3 5 4 6
1
24 18 18 15 0
5
1
5
0 0
0
0
5
2
56 42 42 35 0
22
2
4
4 3
6
5
22
3
80 60 60 50 0
31
3
0
0 0
0 31
31
4
112 84 84 70 0
38
4
0
0 0
0 38
38
Объем 9
4 3
6 74
96
Объем
9
4
3
6
7
4
96

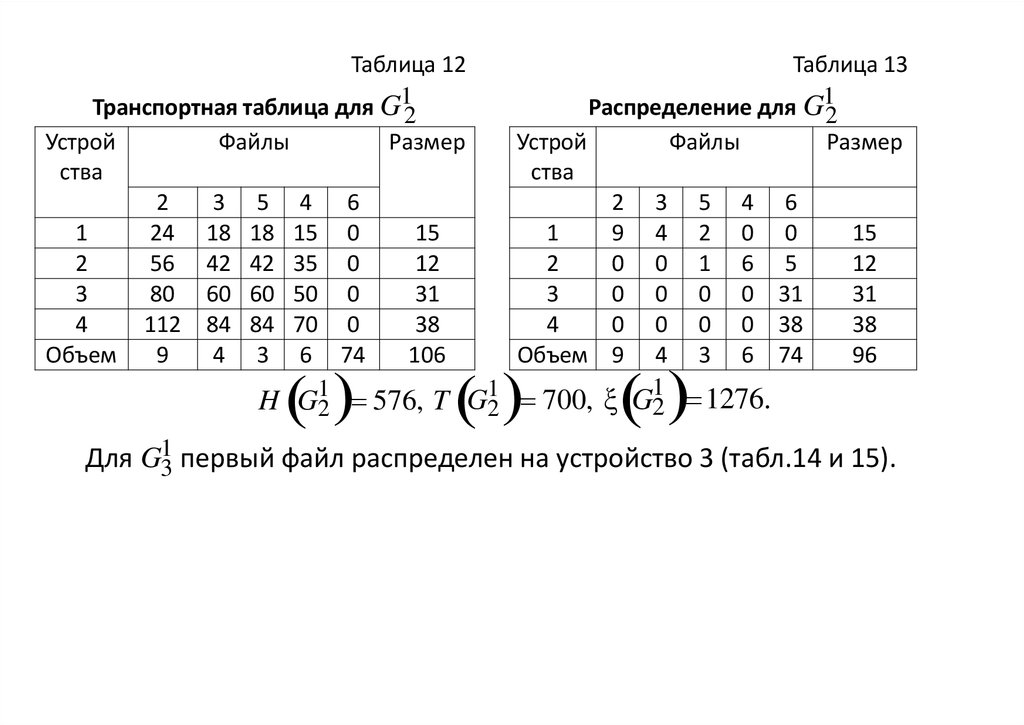
31.

Таблица 12
Таблица 13
Транспортная таблица для G12
Распределение для G12
Устрой
Устрой
Файлы
Размер
Файлы
Размер
ства
ства
2
3 5 4 6
2 3 5 4 6
1
24 18 18 15 0
15
1
9 4 2 0 0
15
2
56 42 42 35 0
12
2
0 0 1 6 5
12
3
80 60 60 50 0
31
3
0 0 0 0 31
31
4
112 84 84 70 0
38
4
0 0 0 0 38
38
Объем
9
4 3 6 74
106
Объем 9 4 3 6 74
96
H G12 576, T G21 700, ξ G21 1276.
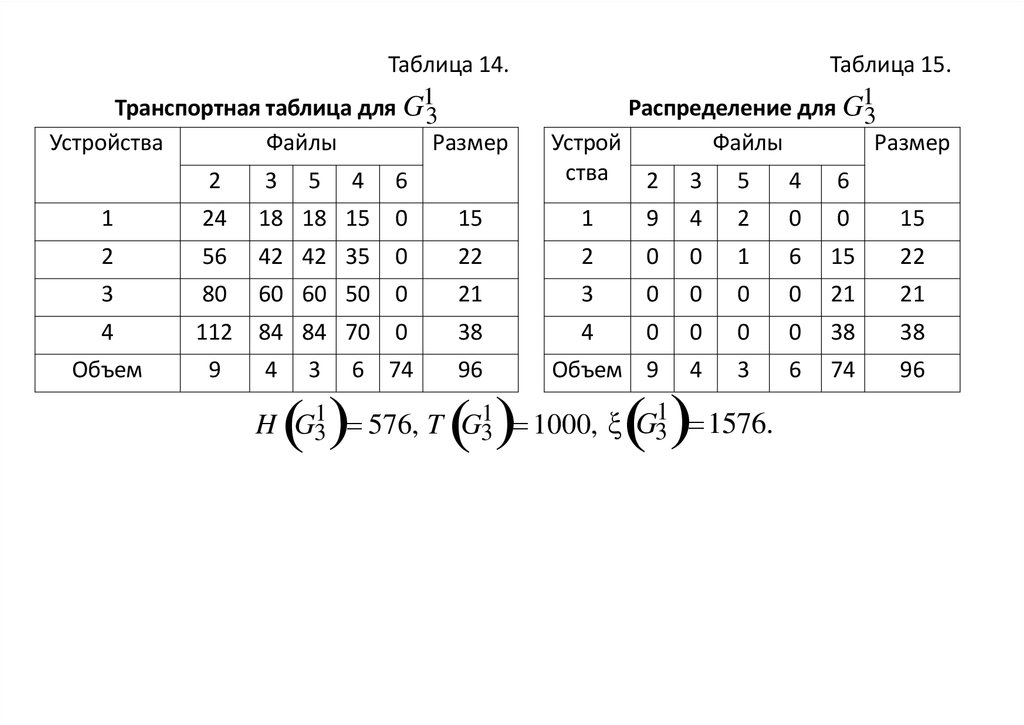
Для G31 первый файл распределен на устройство 3 (табл.14 и 15).

32.

Таблица 14.
Транспортная таблица для G13
Устройства
Файлы
Размер
5
Таблица 15.
Распределение для G13
Устрой
Файлы
Размер
ства
2 3 5
4 6
2
3
4
6
1
24
18 18 15
0
15
1
9
4
2
0
0
15
2
56
42 42 35
0
22
2
0
0
1
6
15
22
3
80
60 60 50
0
21
3
0
0
0
0
21
21
4
112
84 84 70
0
38
4
0
0
0
0
38
38
Объем
9
4
74
96
Объем 9
4
3
6
74
96
3
6
H G31 576, T G31 1000, ξ G31 1576.

33.

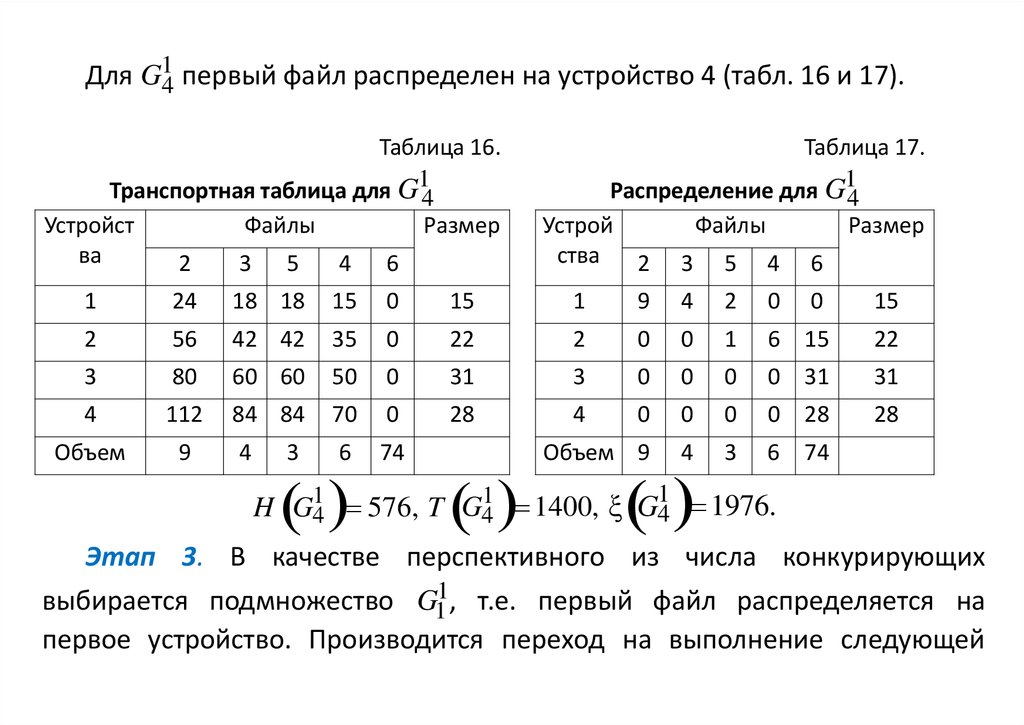
Для G14 первый файл распределен на устройство 4 (табл. 16 и 17).
Таблица 16.
Транспортная таблица для G14
Устройст
Файлы
Размер
ва
2
3 5
4 6
Таблица 17.
Распределение для G14
Устрой
Файлы
Размер
ства
2 3 5 4 6
1
24
18 18
15
0
15
1
9
4
2
0
0
15
2
56
42 42
35
0
22
2
0
0
1
6 15
22
3
80
60 60
50
0
31
3
0
0
0
0 31
31
4
112
84 84
70
0
28
4
0
0
0
0 28
28
Объем
9
4
6
74
Объем 9
4
3
6
3
74
H G14 576, T G41 1400, ξ G41 1976.
Этап 3. В качестве перспективного из числа конкурирующих
выбирается подмножество G11, т.е. первый файл распределяется на
первое устройство. Производится переход на выполнение следующей

34.

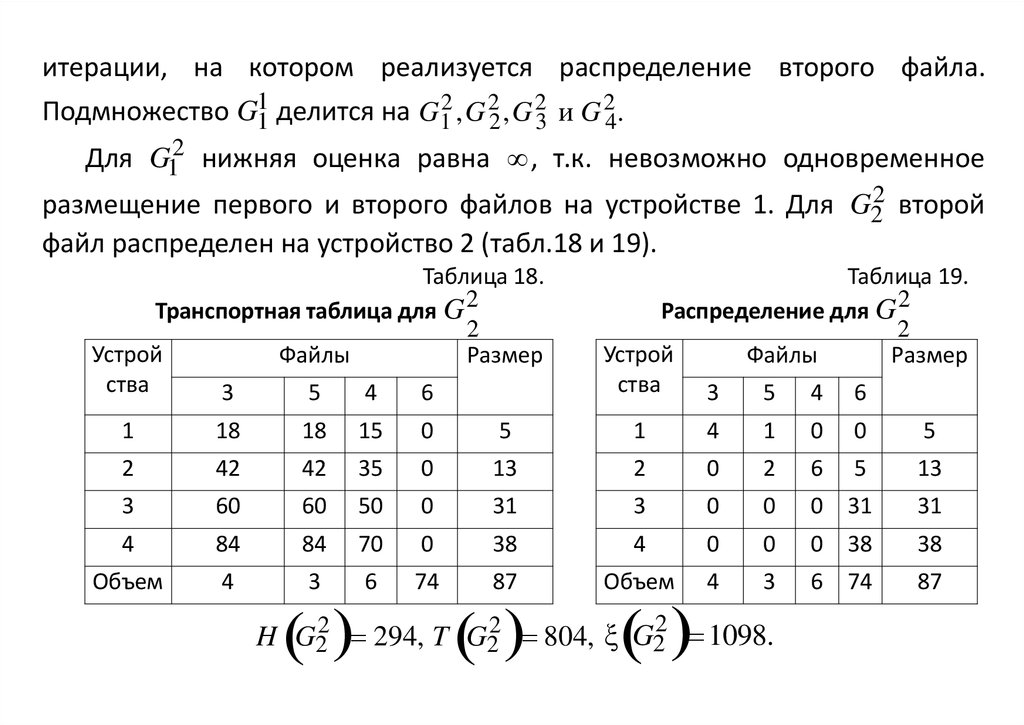
итерации, на котором реализуется распределение второго файла.
Подмножество G11 делится на G 12 ,G 22 ,G 23 и G 24.
Для G12 нижняя оценка равна , т.к. невозможно одновременное
размещение первого и второго файлов на устройстве 1. Для G22 второй
файл распределен на устройство 2 (табл.18 и 19).
Таблица 18.
Транспортная таблица для G 2
2
Устрой
Файлы
Размер
ства
3
5
4
6
Таблица 19.
Распределение для G 2
2
Устрой
Файлы
Размер
ства
3
5 4 6
1
18
18
15
0
5
1
4
1
0
0
5
2
42
42
35
0
13
2
0
2
6
5
13
3
60
60
50
0
31
3
0
0
0 31
31
4
84
84
70
0
38
4
0
0
0 38
38
Объем
4
3
6
74
87
Объем
4
3
6 74
87
H G22 294, T G22 804, ξ G22 1098.

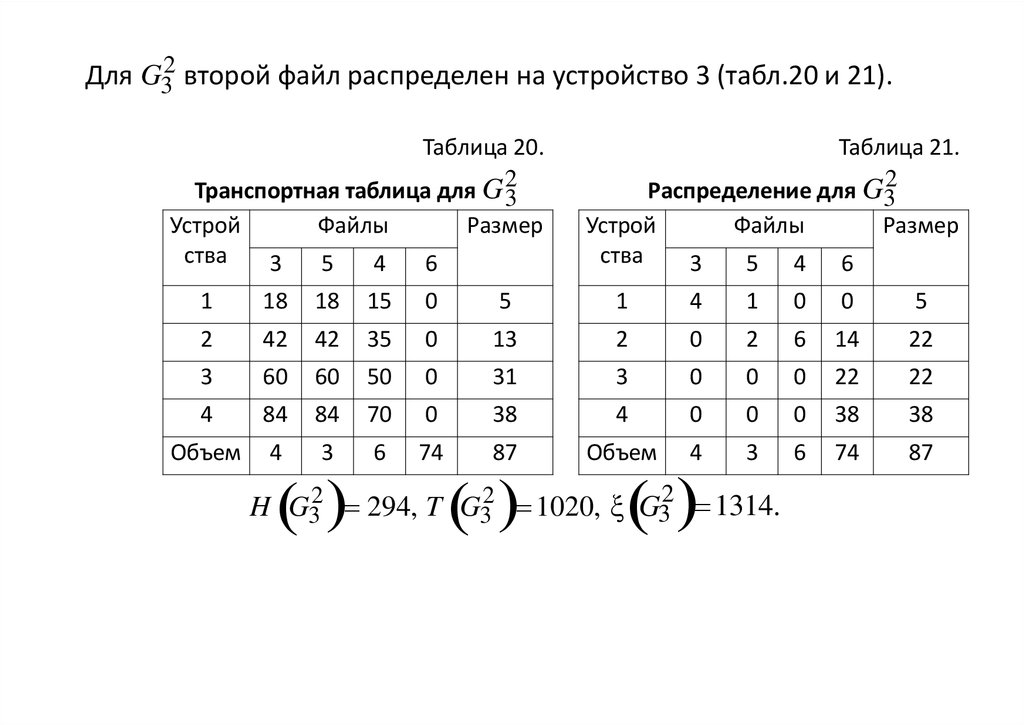
35.

Для G32 второй файл распределен на устройство 3 (табл.20 и 21).
Таблица 20.
Транспортная таблица для G 23
Устрой
Файлы
Размер
ства
3
5
4
6
Таблица 21.
Распределение для G32
Устрой
Файлы
Размер
ства
3
5 4 6
1
18
18
15
0
5
1
4
1
0
0
5
2
42
42
35
0
13
2
0
2
6
14
22
3
60
60
50
0
31
3
0
0
0
22
22
4
84
84
70
0
38
4
0
0
0
38
38
Объем
4
3
6
74
87
Объем
4
3
6
74
87
H G32 294, T G32 1020, ξ G32 1314.

36.

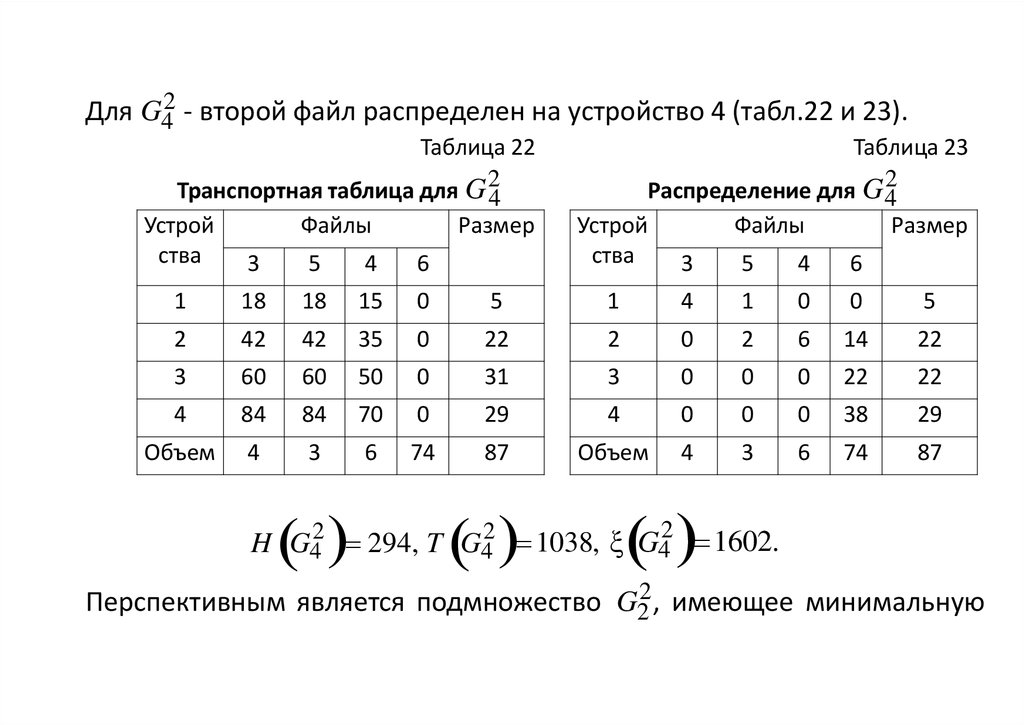
Для G42 - второй файл распределен на устройство 4 (табл.22 и 23).
Таблица 22
Транспортная таблица для G 24
Устрой
Файлы
Размер
ства
3
5
4
6
Таблица 23
Распределение для G 42
Устрой
Файлы
Размер
ства
3
5
4
6
1
18
18
15
0
5
1
4
1
0
0
5
2
42
42
35
0
22
2
0
2
6
14
22
3
60
60
50
0
31
3
0
0
0
22
22
4
84
84
70
0
29
4
0
0
0
38
29
Объем
4
3
6
74
87
Объем
4
3
6
74
87
H G42 294, T G42 1038, ξ G42 1602.
Перспективным является подмножество G22 , имеющее минимальную

37.

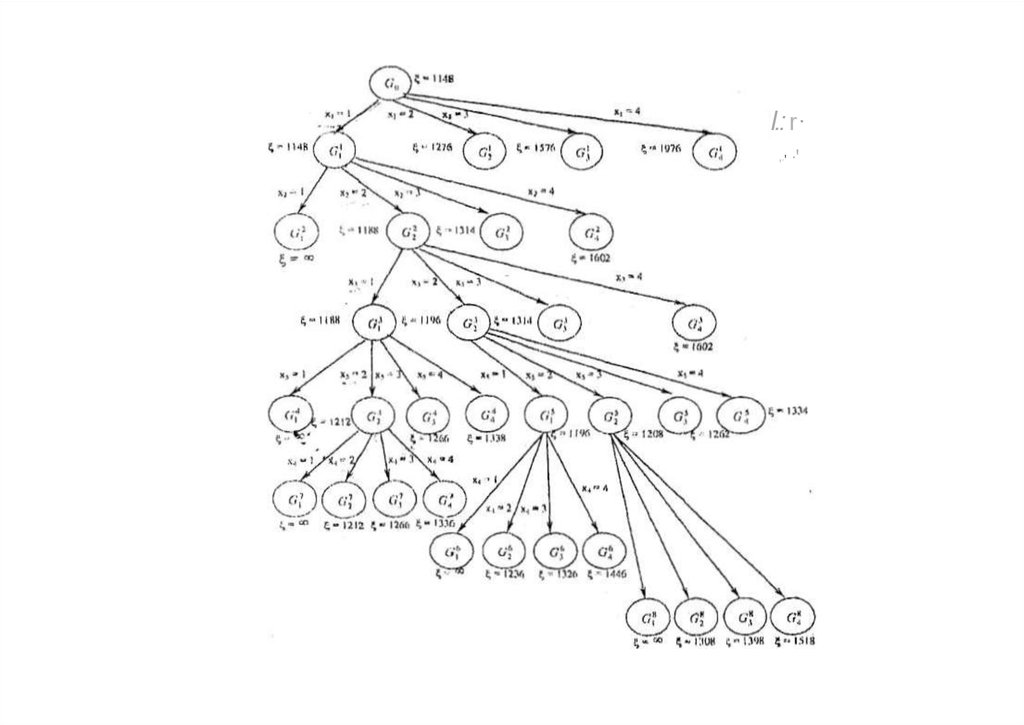
нижнюю оценку ξ G22 1098.
• На рис. приведена процедура дальнейшего распределения файлов по
уровням памяти.
• Оптимальное размещение определяется следующим набором
переменных: x1 1, x2 2, x3 1, x4 2, x5 2.
• Минимальное время доступа к массивам составляет 1212 единиц
времени.

38.

I.: r·
'·' ·'

39.

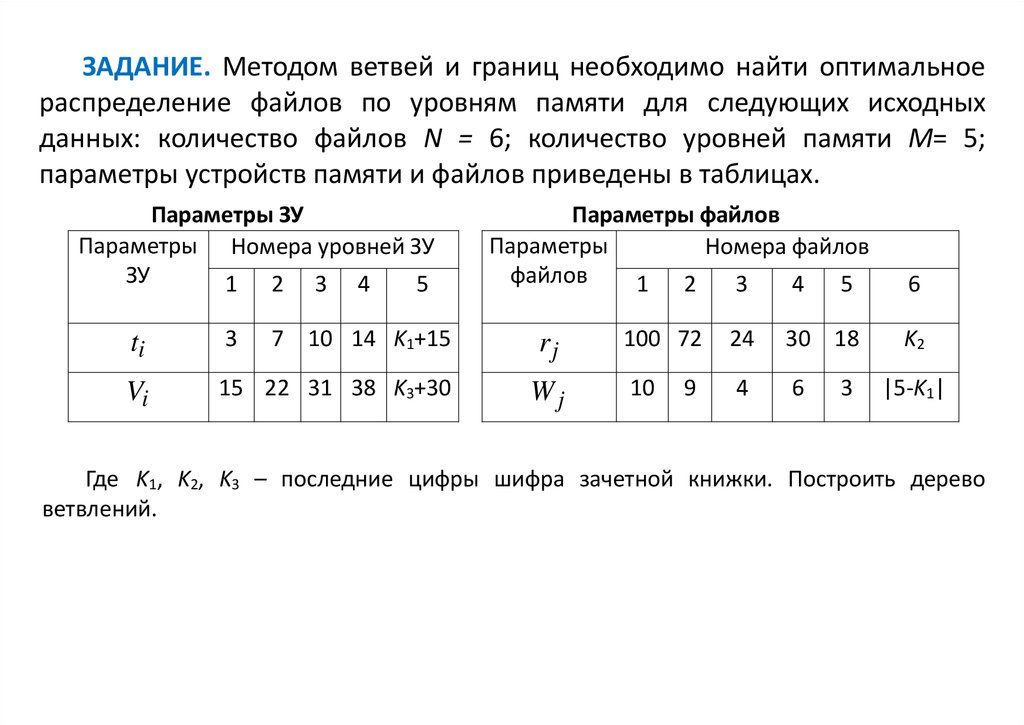
ЗАДАНИЕ. Методом ветвей и границ необходимо найти оптимальное
распределение файлов по уровням памяти для следующих исходных
данных: количество файлов N = 6; количество уровней памяти M= 5;
параметры устройств памяти и файлов приведены в таблицах.
Параметры ЗУ
Параметры Номера уровней ЗУ
ЗУ
1 2 3 4
5
Параметры файлов
Параметры
Номера файлов
файлов
1 2
3
4 5
ti
3
7 10 14 K1+15
rj
Vi
15 22 31 38 K3+30
Wj
100 72
24
30 18
10
4
6
9
3
6
K2
|5-K1|
Где K1, K2, K3 – последние цифры шифра зачетной книжки. Построить дерево
ветвлений.