Алгоритм решения задачи

1.

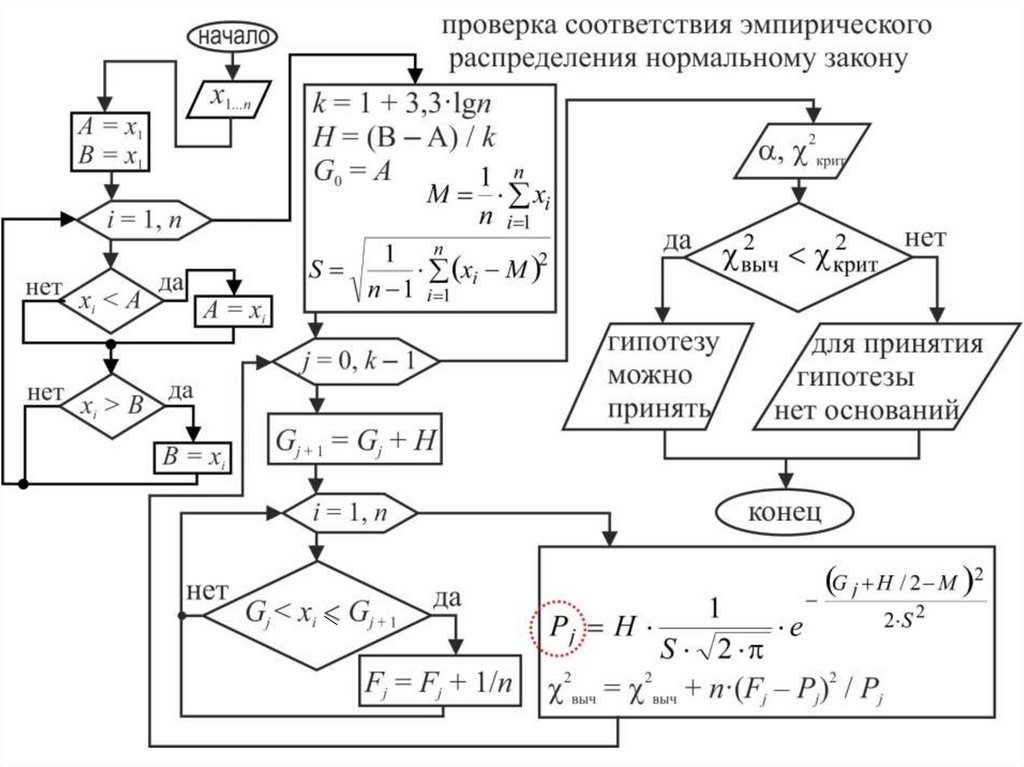
Проверка соответствия эмпирического распределения
нормальному закону
1. Задать число n точек массива исходных данных.
Вычислить число интервалов k = 1 + 3,3·lgn.
2. Ввести элементы массива исходных данных:
x1, x2, …, xn .
Найти А – минимальное значение среди x1, …, xn;
В – максимальное значение среди x1, x2, …, xn.
3. Вычислить длину интервала Н = (В – А) / k. Установить левую границу начального интервала G0 = A.
Учесть x1 при подсчёте эмпирической частоты 0-го
интервала: F0 = n – 1.
n
1
4. Вычислить среднее значение М: М n xi
i 1
n
и стандартное отклонение: S n 1 xi M 2
1
i 1

2.

Основной вычислительный цикл
5. В цикле (по j от 0 до k – 1) перебирать все интервалы
5.1 Вычислить координату правой границы j-го интервала: Gj + 1 = Gj + H.
5.2 Во вложенном цикле (по i) подсчитать эмпирические частоты: Fj = Fj + n–1 (если Gj< xi Gj + 1 )
5.3 Вычислять для каж
G j H 2 M 2
H
2
дого интервала теорети2
S
Pj
e
ческую частоту:
S 2
5.4 В этом же основном
k 1
2
цикле по j подсчитывать выч
n F j Pj 2 Pj
j 0
критерий Пирсона:
2
2
6. Сравнить выч
с критическим значением крит
, взятым из таблицы. Если при числе степеней свободы рав2
2
ным (k – 3) получено, что выч
, то гипотеза
крит
принимается на уровне значимости .