Similar presentations:
Цифровая обработка сигналов при нескольких скоростях. Децимация
1.
Цифровая обработка сигналов при несколькихскоростях
1
2. Децимация
y m w mMh k x mM k ,
k
где
w n
h k x n k .
k
2
3.
Децимация3
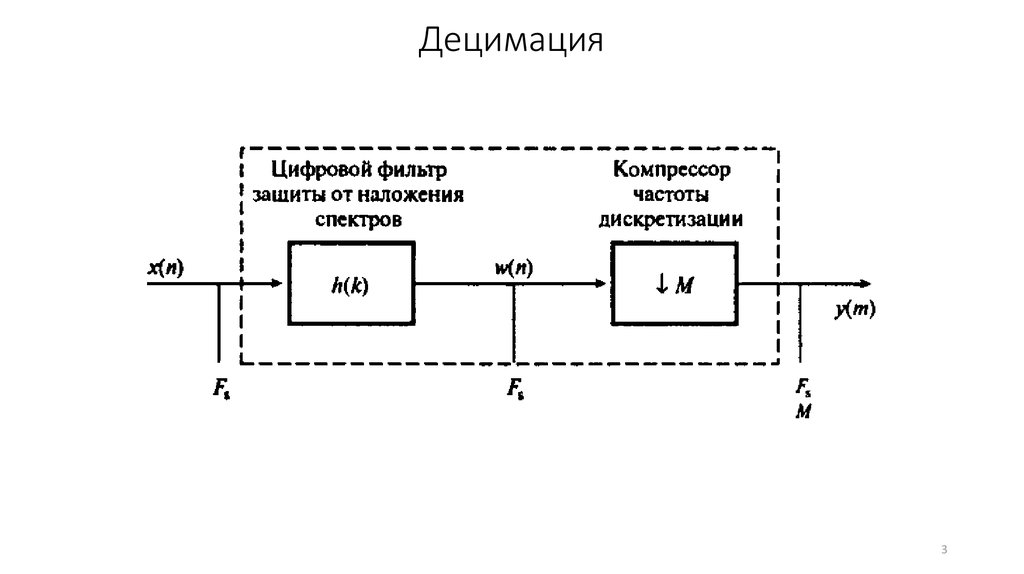
4. Децимация
Для предотвращения наложения при более низкойчастоте выборки используется цифровой фильтр,
предварительно ограничивающий полосу входного
сигнала до Fs/2
4
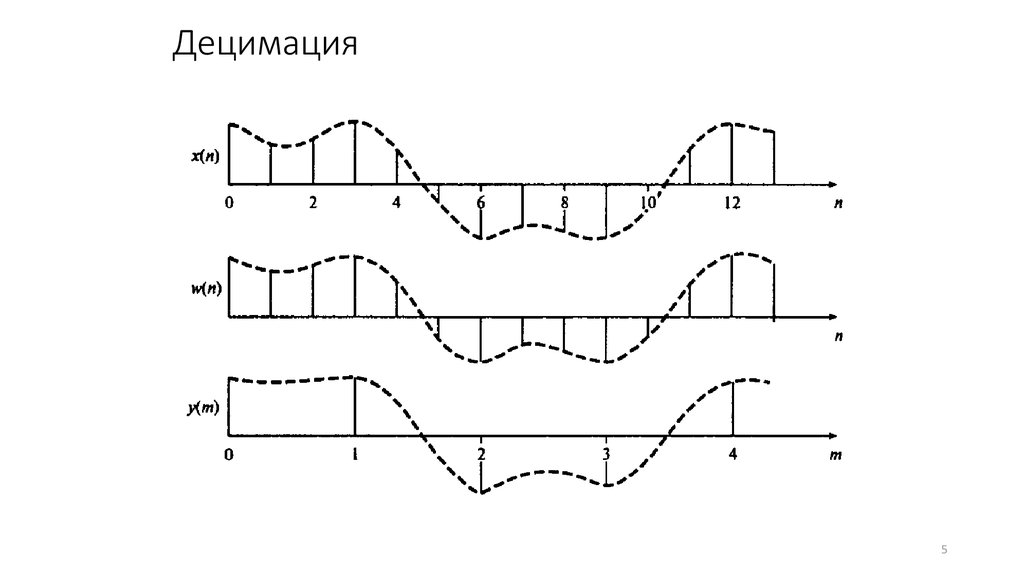
5. Децимация
56. Спектральная интерпретация децимации
67.
Интерполяцияy m
h k w m k ,
k
m
x ,
где w m L
0
m 0, L, 2 L,...
7
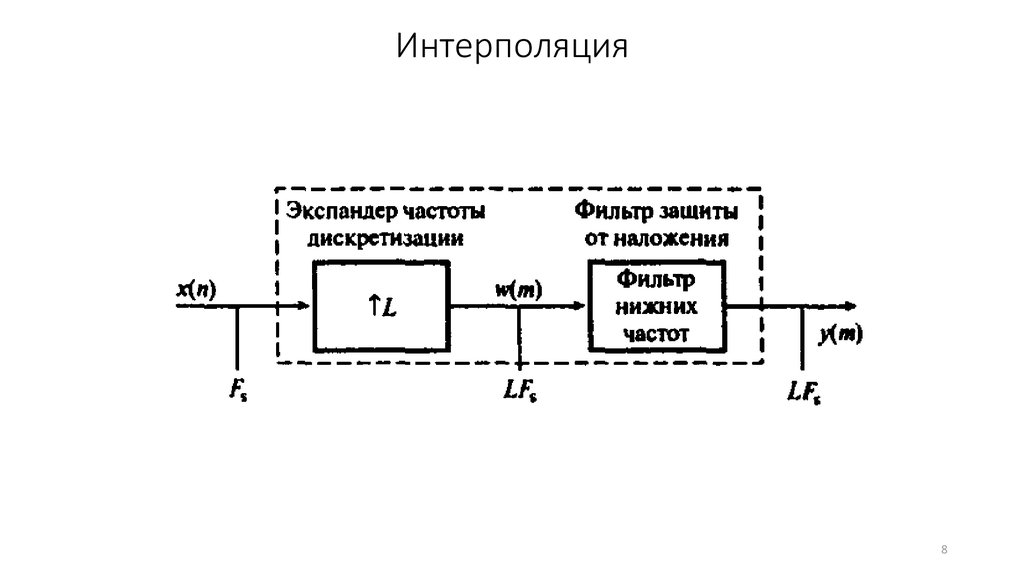
8.
Интерполяция8
9.
Интерполяция9
10. Спектральная интерпретация интерполяции
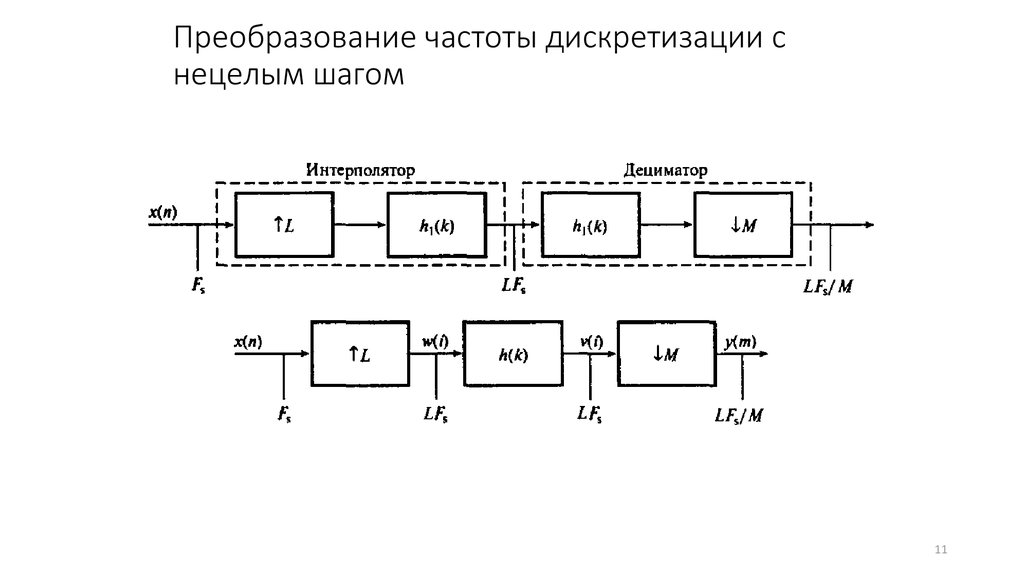
1011. Преобразование частоты дискретизации с нецелым шагом
1112.
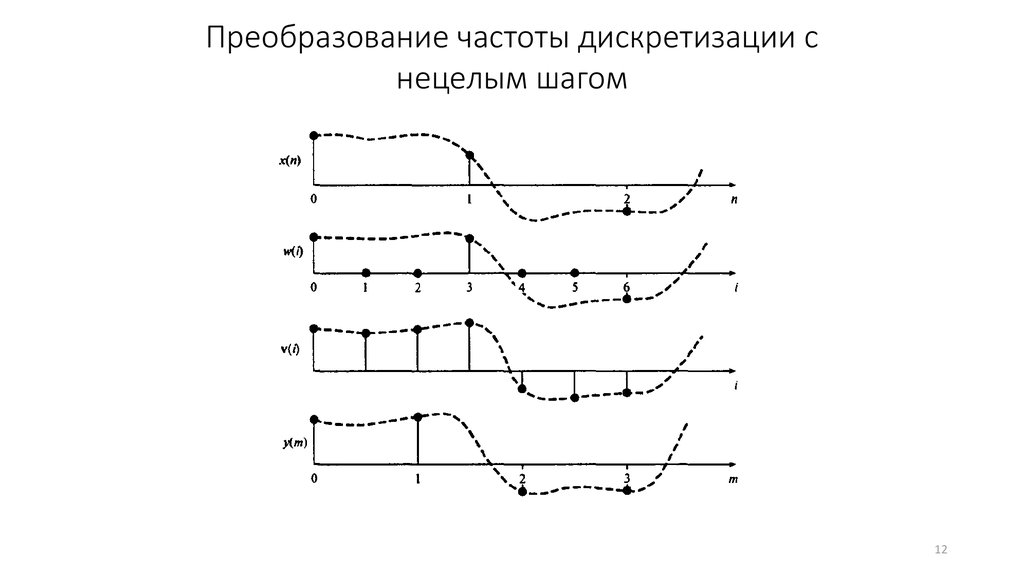
Преобразование частоты дискретизации снецелым шагом
12
13. Разработка практических конвертеров частоты дискретизации
1. Задать общие требования к фильтрам защиты от наложенияспектров и подавления зеркальных частот.
2. Определить оптимальное число каскадов децимации или
интерполяции, дающих наиболее эффективную реализацию.
3. Определить для каждого каскада шаги децимации или
интерполяции.
4. Разработать для каждого каскада подходящий фильтр.
13
14. Требования к фильтру дециматора:
полоса пропускания 0 ≤ f ≤ fрполоса подавления FS/2M ≤ f ≤ FS/2
отклонение в полосе пропускания δp
отклонение в полосе подавления δs
где fP ≤ FS/2M, а FS – исходная частота дискретизации
14
15. Требования к фильтру интерполятора:
полоса пропускания 0 ≤ f ≤ fрполоса подавления FS/2 ≤ f ≤ LFS/2
отклонение в полосе пропускания δp
отклонение в полосе подавления δs
где fP ≤ FS/2M
15
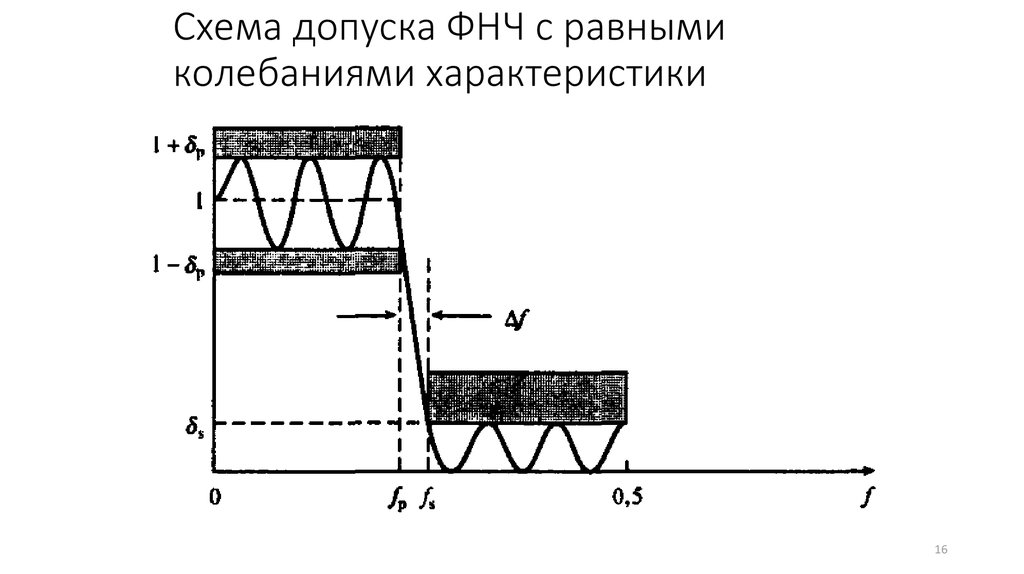
16. Схема допуска ФНЧ с равными колебаниями характеристики
1617. Многокаскадная структура
1718. Спецификации фильтра i-го каскада, i = 1, 2, … I
1819. Требования к фильтрам отдельных каскадов на примере дециматора:
полоса пропускания 0 ≤ f ≤ fрполоса подавления (Fi-FS/2M ) ≤ f ≤ Fi-1/2, i=1,2,…I
отклонение в полосе пропускания δp/I
отклонение в полосе подавления δs
где Fi – частота дискретизации на выходе i-го каскада, Fi
= Fi-1/Mi
19
20. Определение числа каскадов и шагов децимации
Критерии оптимальности:I
Число операций умножения в секунду
УВС N i Fi ,
i 1
где Ni – число коэффициентов фильтра i-го каскада
I
Общая требуемая память:
ОТП N i
i 1
20
21.
Целесообразно определить все возможные множители M, т.е. весьнабор значений Mi и соответствующие им параметры УВС и ОТП.
Затем следует методом перебора выбрать наиболее эффективное
или предпочтительное решение.
21
22.
Шаги децимации должны удовлетворятьследующему соотношению:
M1>M2>…>MI
22
23.
При I=2 (т.е. для двухкаскадного дециматора)оптимальные значения шагов децимации,
минимизирующие параметр ОТП, равны
M 1opt
2M
,
1/2
2 f (2 M f )
M 2 opt
M
,
M 1opt
23
24. Простая схема дециматора (а), функциональная схема прохождения сигнала через дециматор (б)
2425.
Если фильтр реализован в прямой форме (т.е.используются линии задержки с отводами), выход
фильтра ω(n) и его вход x(n) связаны следующим
соотношением:
N 1
(n) h(k ) x(n k ),
k 0
Поскольку выход дециматора y (m) (mM ),
уравнение дециматора можно записать следующим
образом:
N 1
y (m) h(k ) x( Mm k ).
k 0
25
26. Более эффективная диаграмма прохождения сигнала через дециматор
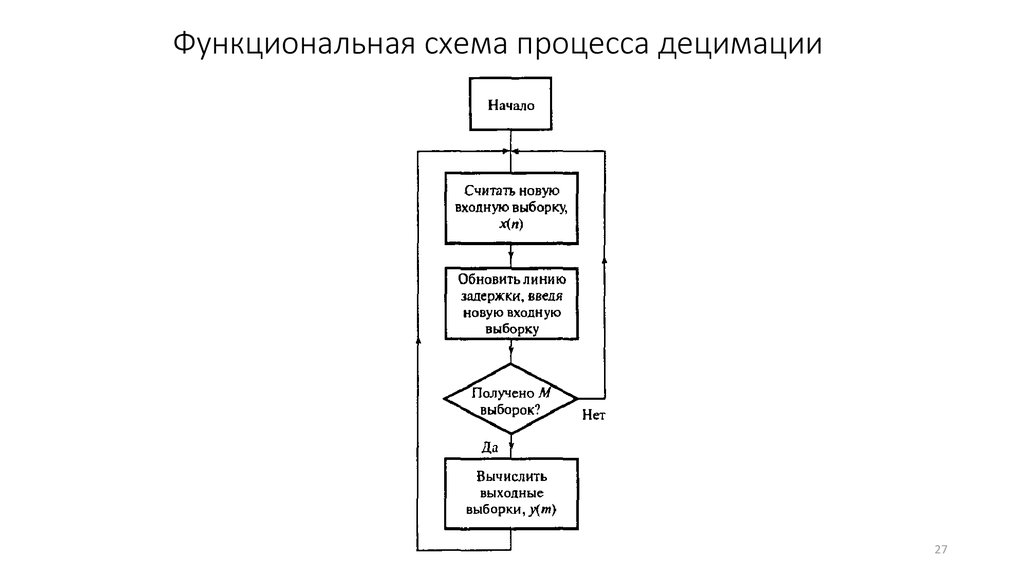
2627. Функциональная схема процесса децимации
2728. Выходная задержка дециматора
T(1 каскад) = 1 T1 M 1 выборок,M
1
T(2 каскада) =
T1 M 1T2 M 1M 2 1 выборок,
M 1M 2
T(3 каскада) =
1
T1 M 1T2 M 1M 2T3 M 1M 2 M 3 1
M 1M 2 M 3
выборок, где Ti – задержка фильтра i-го каскада:
Ti N i 1 / 2 выборок
28
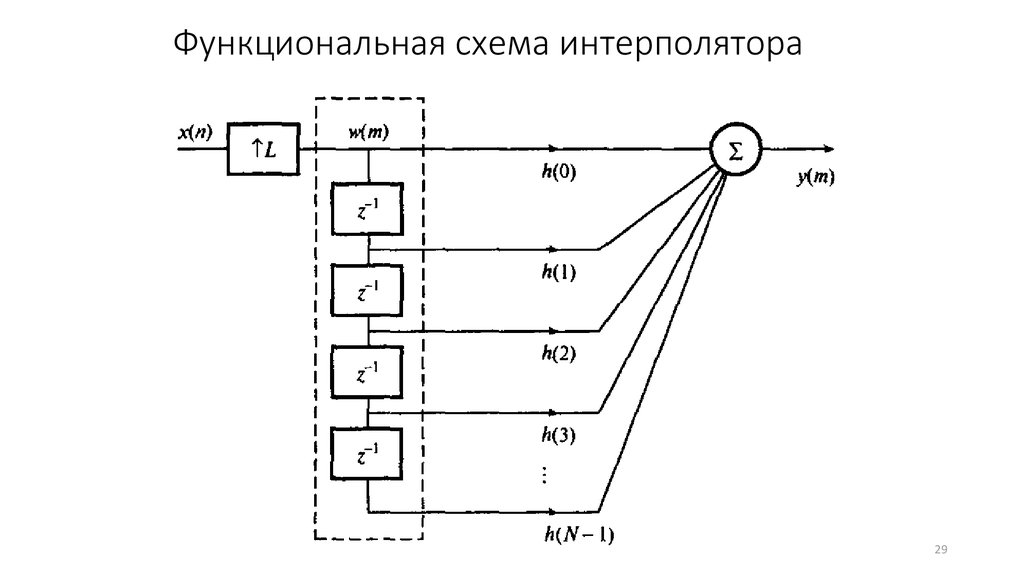
29. Функциональная схема интерполятора
2930.
Функциональная схема процесса интерполяции30
31. Выходная задержка интерполятора
T(1 каскад) = T1 выборок,T(2 каскада) = (T1 + M1T2) выборок,
T(3 каскада) = (T1 + M1T2 + M1M2T3) выборок, где Ti –
задержка фильтра i-го каскада:
Ti N i 1 / 2 выборок
31

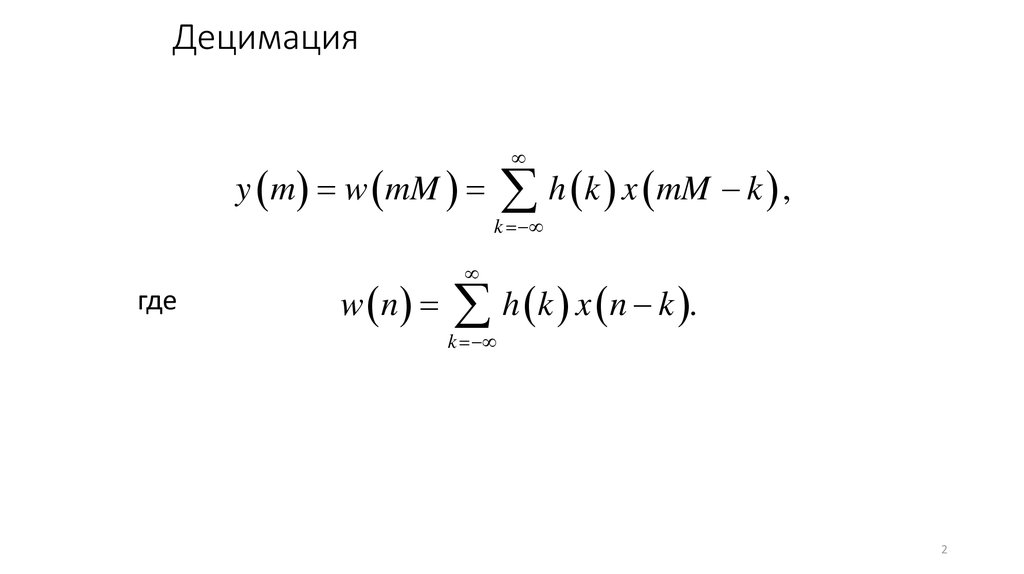





















 electronics
electronics








