Similar presentations:
Временная оценка денежных потоков. (Лекция 3)
1. Временная оценка денежных потоков
Московский Государственный Университет Геодезии и Картографии (МИИГАиК)Временная оценка денежных
потоков
Лектор Голубев В.В.
2. Простой и сложный проценты
При простом проценте ставка начисляется на первоначальновложенную сумму инвестиций. При сложном проценте, каждое
новое начисление процентов осуществляется с учетом
накоплений в предыдущий период.
Начисление по простому проценту
1
2
n
3 ….. n
S =(1+in)
Начисления по сложному
проценту
1
2
3 …..
n
S =(1+i)
n
n
3. Пример использования сложного процента
В 1626 году индейцы продали остров Манхэттен Питеру Миньютуза товары, стоимостью 24$.
Простой процент i=6%
24$
БАНК
1626
24$
572$
2007
Сложный процент i=6%
100млрд.$
БАНК
4. Пример использования сложного процента
Простой процент i=7%24$
664$
БАНК
2007
1626
Сложный процент i=7%
24$
БАНК
3720млрд.$
5. Накопление и дисконтирование
Основными операциями, которые позволяют сопоставлятьденьги в разное время, являются операции накопления и
дисконтирования.
НАКОПЛЕНИЕ – процесс определения
будущей стоимости денег.
PV
FV
ДИСКОНТИРОВАНИЕ –
Процесс приведения
денежных поступлений от
инвестиций к их текущей
стоимости
6. Функция: накопленная сумма денежной единицы (будущая стоимость единицы)
Функция определяет будущую стоимость денежной единицычерез n лет.
n
n
При ежегодном начислении процентов
S =(1+i)
FV=PV (1+i)
n
S =(1+i/k)
n
При начислении
процентов k раз в год
nk
FV=PV (1+i/k)
nk
n
S
k
iэф.=(1+i/k) -1
PV 1
iэф.=(1+0,12/4)4-1=0,1255
ПРАВИЛО 72.
Примерный срок удвоения капитала равен
N=72/i
1
FV
2
3 …..
n
7. Функция: текущая стоимость денежной единицы (реверсия)
Функция определяет текущую стоимость денежной единицыпри известной будущей, через n лет.
n
1
S
Х
1
1
1
X
n
n
(
1
i
)
S
1
PV FV 1 FV
n
n
(
1
i
)
S
1
PV
х
1
FV
n
S
8. Текущая и будущая стоимости аннуитета
Аннуитет – серия равновеликих платежей, отстоящих один отдругого на один и тот же промежуток времени.
1
2
3 ….. n
Текущая
стоимость
аннуитета
1 2 ….. n
Будущая
стоимость
аннуитета
1
2
3 ….. n
9. Текущая стоимость аннуитета
Обычный аннуитет – аннуитет, при котором платежиосуществляются в конце каждого периода начисления
процентов.
Текущая
стоимость
аннуитета
PMT – периодический
платеж
an
1 1
1
PMT
1
1
n
n
1
1
1
1
(
1
i
)
an
...
=
l =(pvaf,i,n)=
1
2
(1 i) (1 i)
(1 i) n
(
1
i
)
l 1
i
1
2
…..
n
1
1
n
1
(1 i ) n
PV=PMT*an=PMT*
l = PMT *
i
l 1 (1 i )
PV = PMT* (pvaf,i,n)
10. Текущая стоимость авансового аннуитета
Авансовый аннуитет – аннуитет, при котором платежиосуществляются в начале каждого периода начисления
процентов.
Авансовая
стоимость
аннуитета
PMT – периодический
платеж
an
1 1
1
PMT
1
1
n 1
n 1
1
1
1
1
(
1
i
)
an
...
= 1+
=
0
1
l = 1
(1 i) (1 i)
(1 i) n 1
(
1
i
)
l 1
i
1
=1+pvaf(i,n-1)
2
n 1
3
…..
n-1
1
PV=PMT*an=PMT*(1+
l )=
(
1
i
)
l 1
1
1
n 1
(
1
i
)
= PMT*( 1
)
i
=PMT*(1+pvaf(i,n-1))
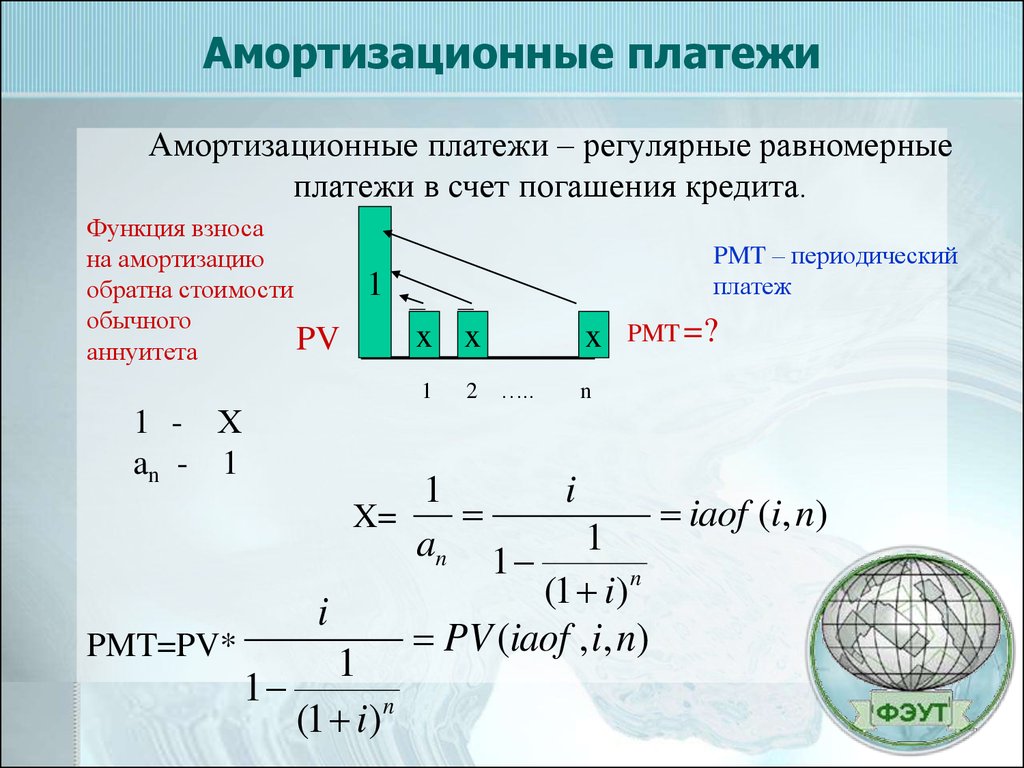
11. Амортизационные платежи
Амортизационные платежи – регулярные равномерныеплатежи в счет погашения кредита.
Функция взноса
на амортизацию
обратна стоимости
обычного
PV
аннуитета
1
x x
1
1 - Х
an - 1
PMT=PV*
PMT – периодический
платеж
i
2
x
…..
PMT =?
n
1
i
iaof (i, n)
X=
an 1 1
(1 i ) n
1
1
(1 i) n
PV (iaof , i, n)
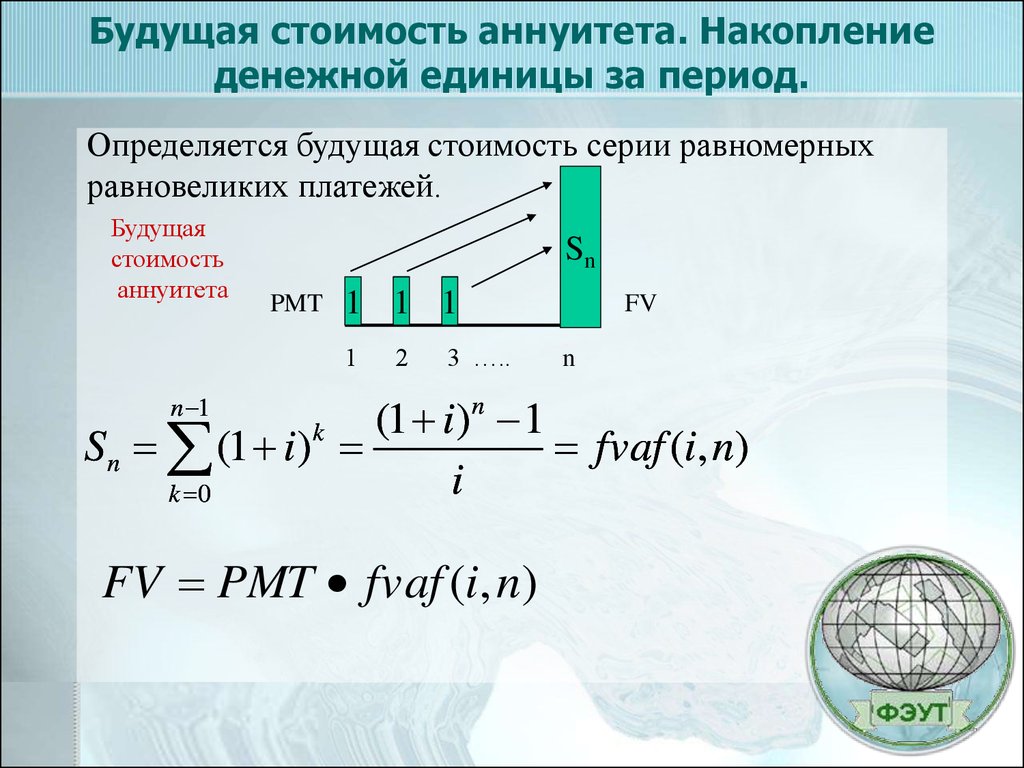
12. Будущая стоимость аннуитета. Накопление денежной единицы за период.
Определяется будущая стоимость серии равномерныхравновеликих платежей.
Будущая
стоимость
аннуитета
Sn
PMT
1 1 1
1
2
FV
3 …..
n
(1 i) 1
Sn (1 i)
fvaf (i, n)
i
k 0
n 1
n
k
FV PMT fvaf (i, n)
13. Будущая стоимость аннуитета. Накопление денежной единицы за период.
(1 i)n 1Sn (1 i)
fvaf (i, n)
i
k 0
n 1
k
период
Начало
Конец
года
Остаток
1
Н
0
к
0
Н
1
к
1.1
Н
2.1
к
2.31
Н
3.31
к
3.641 1
2
3
4
депозит
∑
1
1
1
2.1
1
3.31
4.641
14. Будущая стоимость авансового аннуитета.
(1+ i)n+1 -1Sn = å(1+ i) -1 =
-1 = fvaf (i, n+1) -1
i
k=1
n+1
k
период
Начало
Конец
Остаток
депозит
∑
1
Н
0
1
1
к
1,1
Н
1.1
1
2,1
к
2.31
Н
2.31
1
3.31
к
3.641
Н
3.641
1
4.641
к
5,1051
2
3
4
15. Фонд возмещения
Определяется величина равномерных равновеликих платежей,которые необходимо осуществлять, чтобы к концу срока иметь
на счету заданную сумму денег.
Х
1
- 1
- Sn
Х=1/ Sn
PMT=?
Х Х Х
1
2
3 …..
Sn
=1
FV
n
i
PMT FV
FV sff (i, n)
n
(1 i) 1
16.
http://ozenka.ucoz.ru/index/6funkz/0-57http://www.nwsa.ru/















 finance
finance business
business








