Similar presentations:
Перемещение поршня
1.
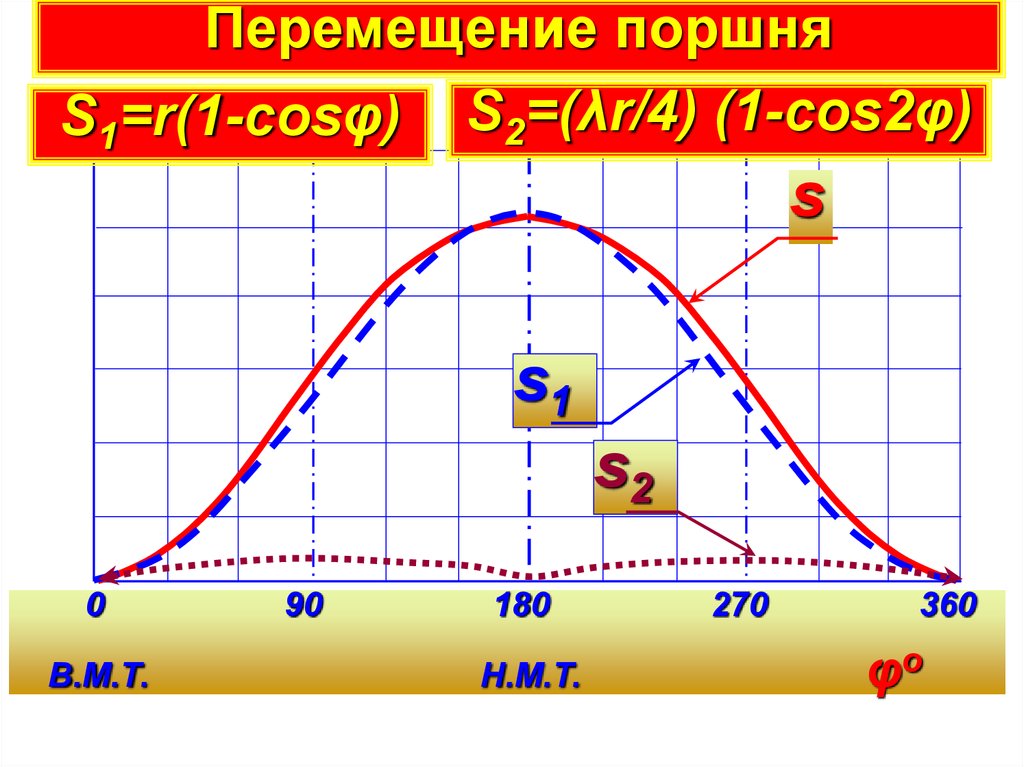
Перемещение поршняS1=r(1-cosφ) S2=(λr/4) (1-cos2φ)
s
s1
s2
0
В.М.Т.
90
180
Н.М.Т.
270
360
φо
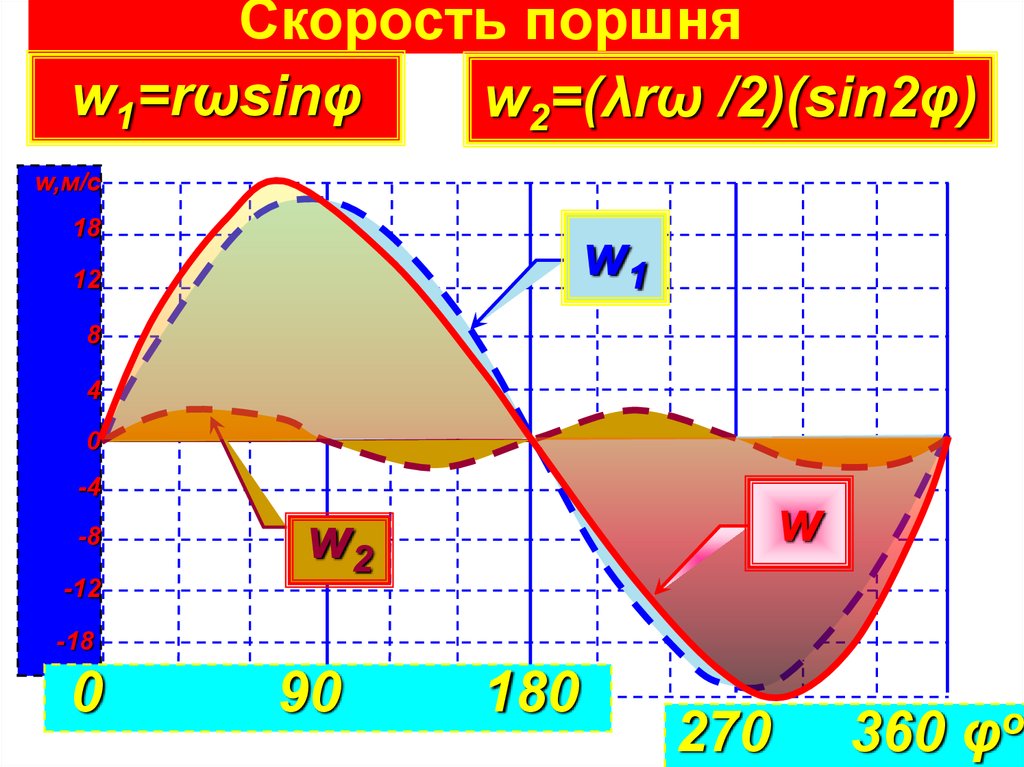
2. Скорость поршня
w1=rωsinφw2=(λrω /2)(sin2φ)
w,м/с
18
w1
12
8
4
0
-4
-8
-12
w
w2
-18
0
90
180
270
360 φо
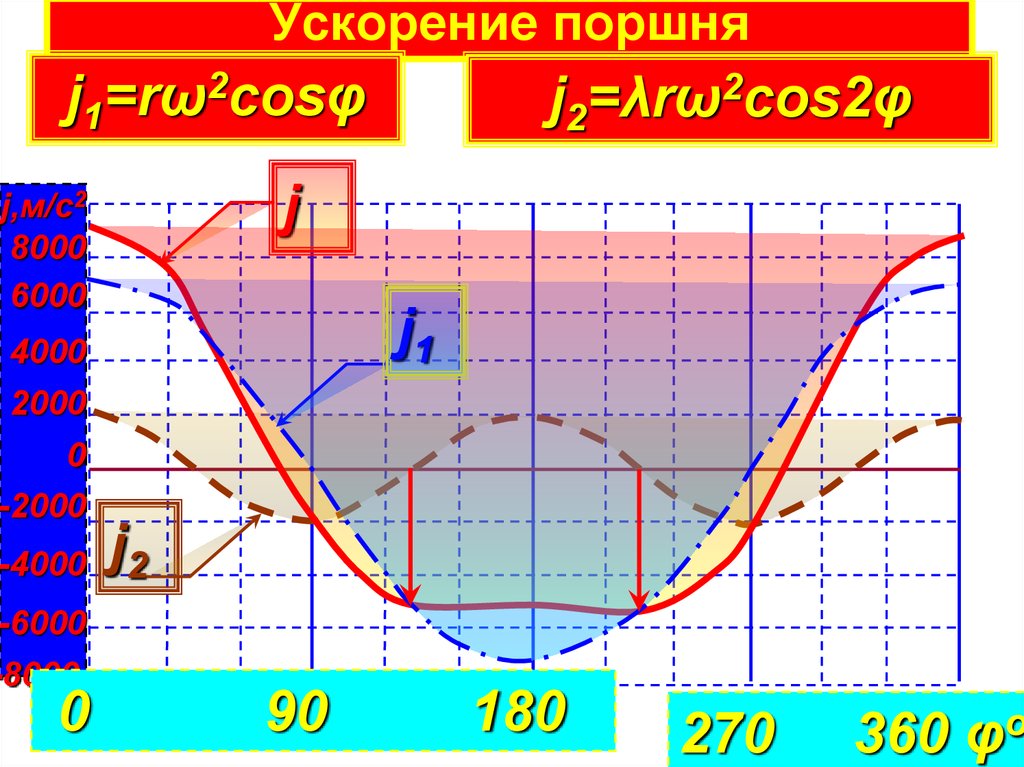
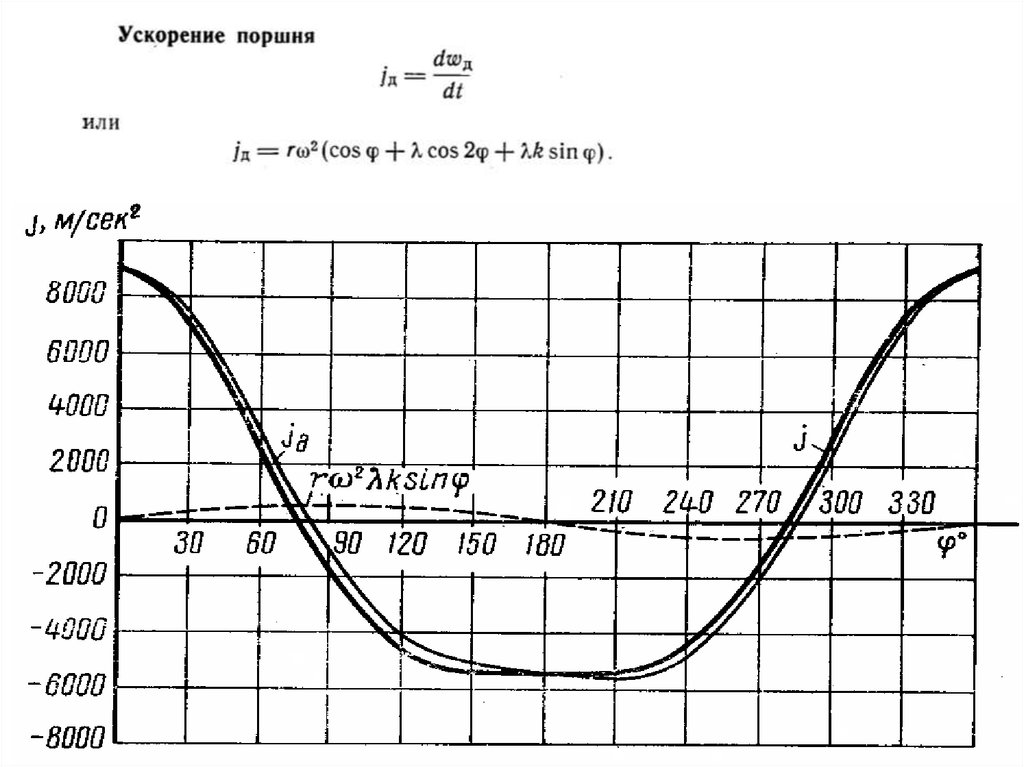
3. Ускорение поршня
j1=rω2cosφj
j,м/с2
8000
6000
j1
4000
2000
0
-2000
-4000
-6000
-8000
0
j2=λrω2cos2φ
j2
90
180
270
360 φо
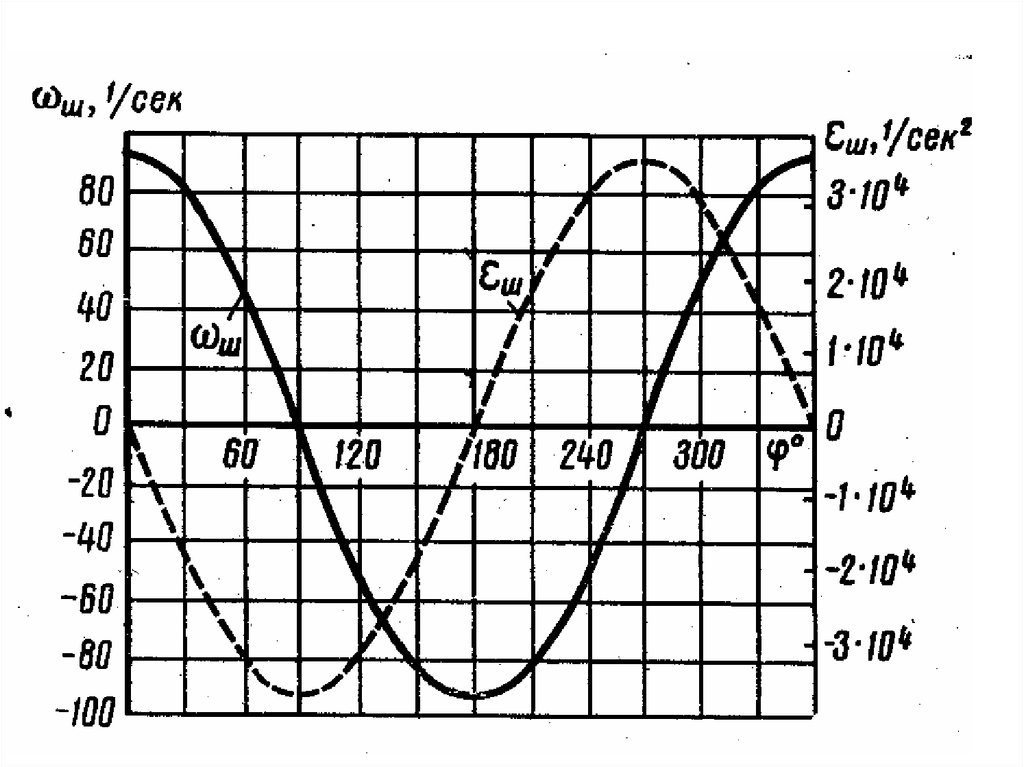
4. Кинематика шатуна
β=arcsin(λsinφ)sinβmax=± λ; βmax=12÷18o; ωш=dβ/dt;
cosβ(dβ/dt)= λcosφ(dφ/dt).
ωш=λω[(cosφ)/ (cosβ)]≈ λω cosφ
Угловое ускорение шатуна
εш=dωш/dt=(dωш/dφ) (dφ/dt)=
=ω(dωш/dφ).
εш=- λω2sinφ
5.
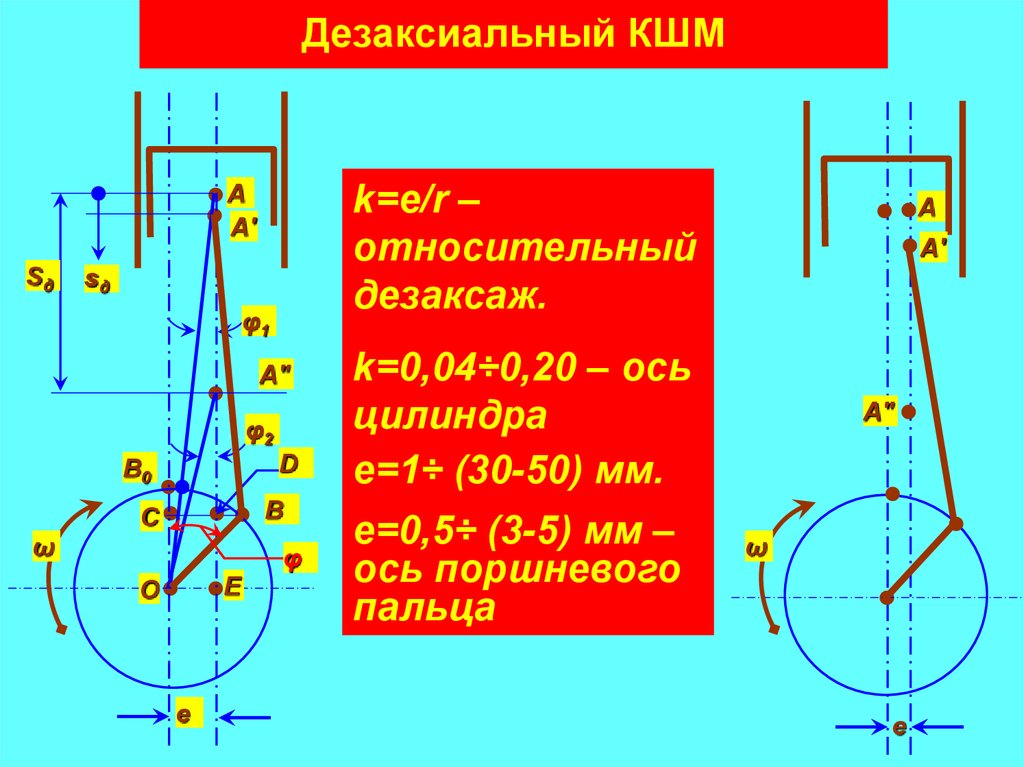
6. Дезаксиальный КШМ
k=e/r –относительный
дезаксаж.
A
A′
Sд
sд
φ1
A″
φ2
D
B0
B
C
ω
φ
E
O
e
A
A′
k=0,04÷0,20 – ось
цилиндра
e=1÷ (30-50) мм.
e=0,5÷ (3-5) мм –
ось поршневого
пальца
A″
ω
e
7.
sд E A E A (l r ) e r cos l cos"
2
2
1
1
2
sд r 1 k cos cos
B C r sin l sin e
2
8.
sin sin k ;cos 1 sin 1 sin k ;
2
2
2
9.
10. Приведение массы шатуна
Условия приведения:1) Сумма всех заменяющих масс должна быть
равна массе шатуна
2) Общий центр тяжести всех заменяющих масс
должен совпадать с ц.т. шатуна и двигаться
по закону движения ц.т. шатуна
3) Сумма моментов инерции всех заменяющих
масс относительно оси, проходящей через
ц.т. шатуна должна быть равна моменту
инерции массы шатуна Iш относительно той
же оси
4) Угловое ускорение заменяющей системы во
вращательном движении по отношению к ее
ц.т. должно быть равно угловому ускорению
шатуна в том же движении
11. Приведение массы шатуна на 3 массы
A′Массы m1, m2, m3 сосредоточены
в точках A′, B и D
Условия приведения
m1
l′
l
β
D
φ
O
m3
B
m2
1) mш= m1+m2+m3
2) m1l′=m2(l-l′)
3) Iш= m1 (l′)2+ m2(l-l′)2
Iш
Iш
m1 ; m2
;
l l
l-l l
Iш
m3 mш
l-l l
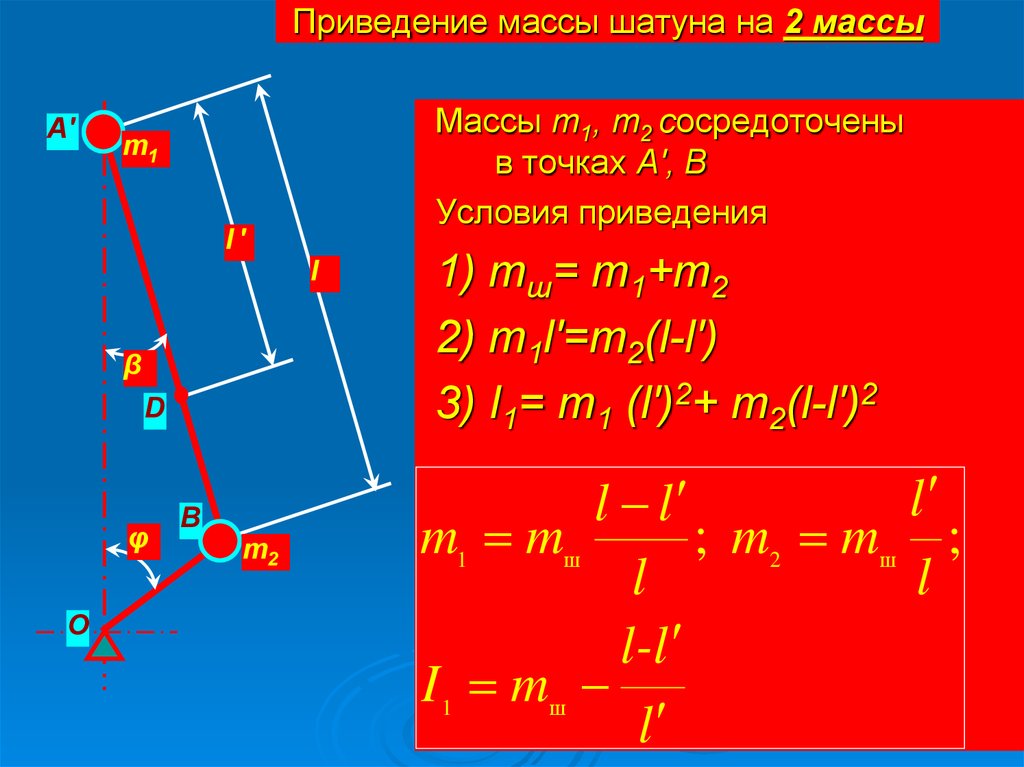
12. Приведение массы шатуна на 2 массы
A′Массы m1, m2 сосредоточены
в точках A′, B
Условия приведения
m1
l′
l
β
D
φ
O
B
m2
1) mш= m1+m2
2) m1l′=m2(l-l′)
3) I1= m1 (l′)2+ m2(l-l′)2
l
l l
m1 mш
; m2 mш ;
l
l
l-l
I 1 mш
l
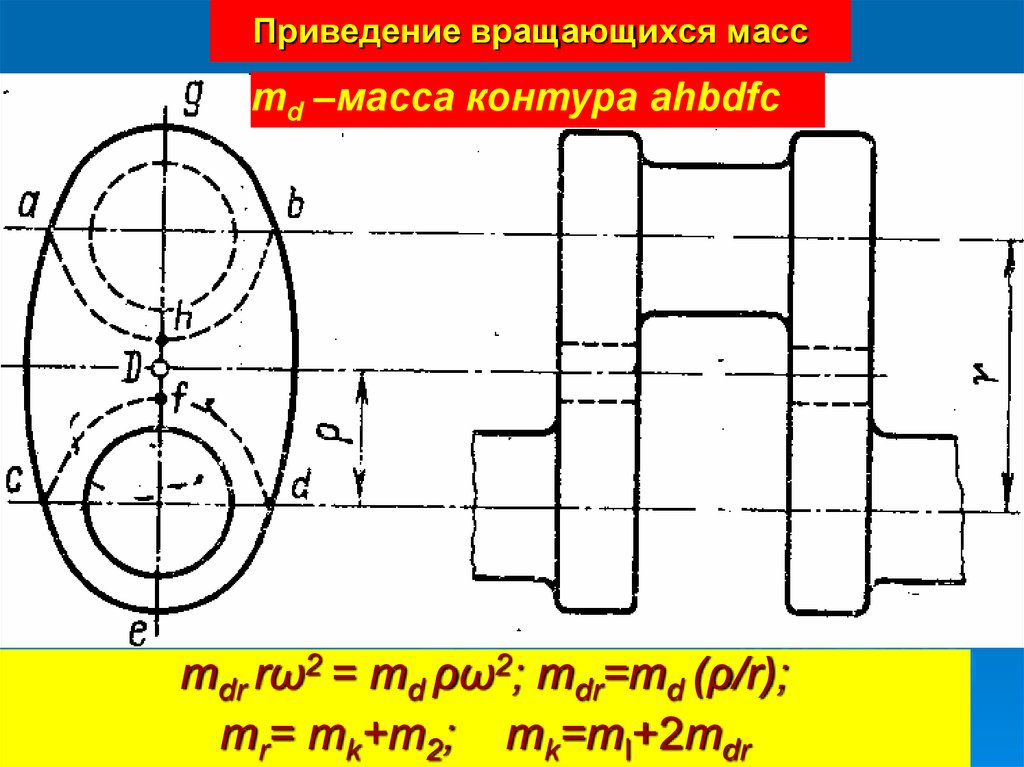
13. Приведение вращающихся масс
md –масса контура ahbdfcmdr rω2 = md ρω2; mdr=md (ρ/r);
mr= mk+m2; mk=mI+2mdr
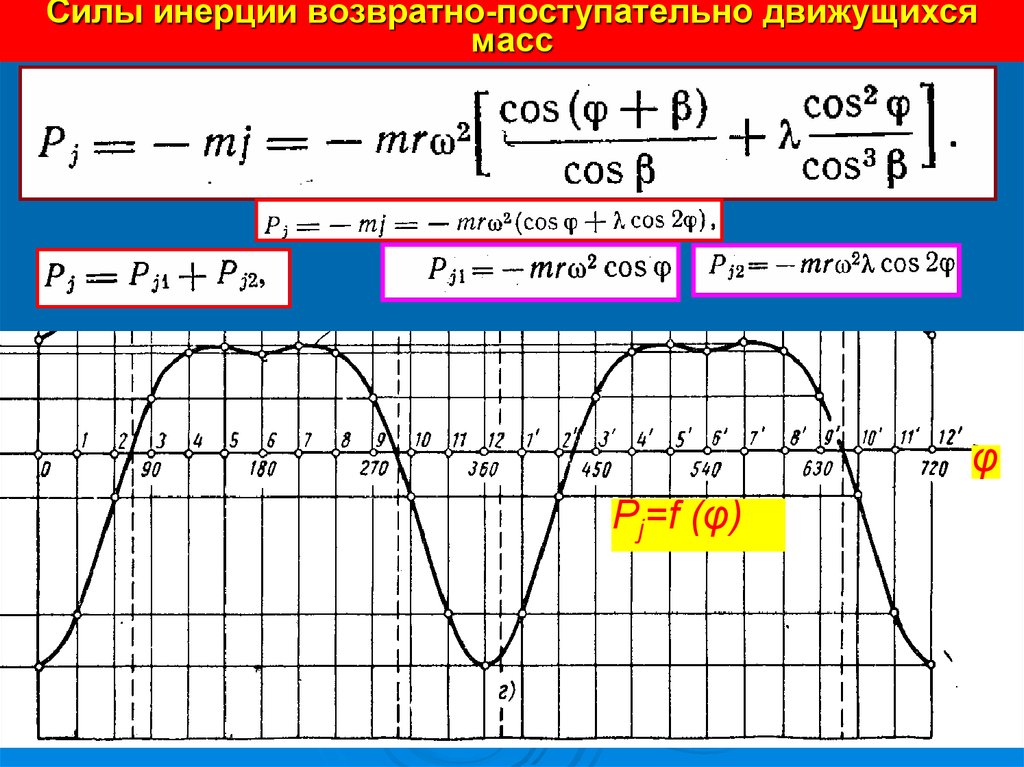
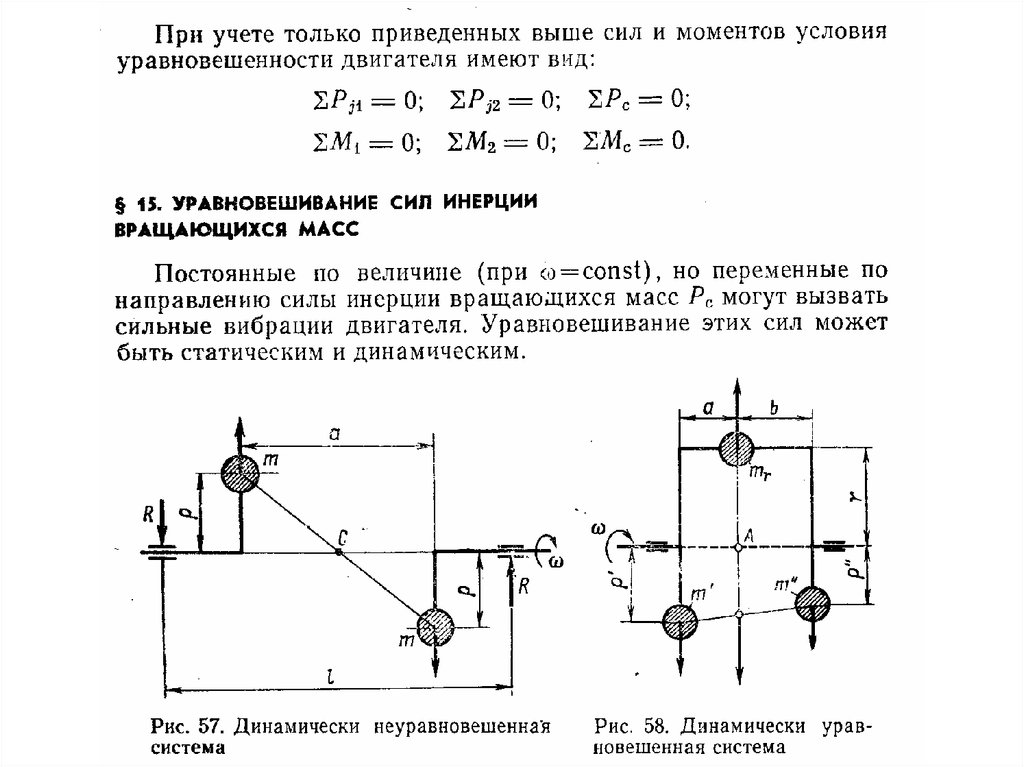
14. Силы инерции возвратно-поступательно движущихся масс
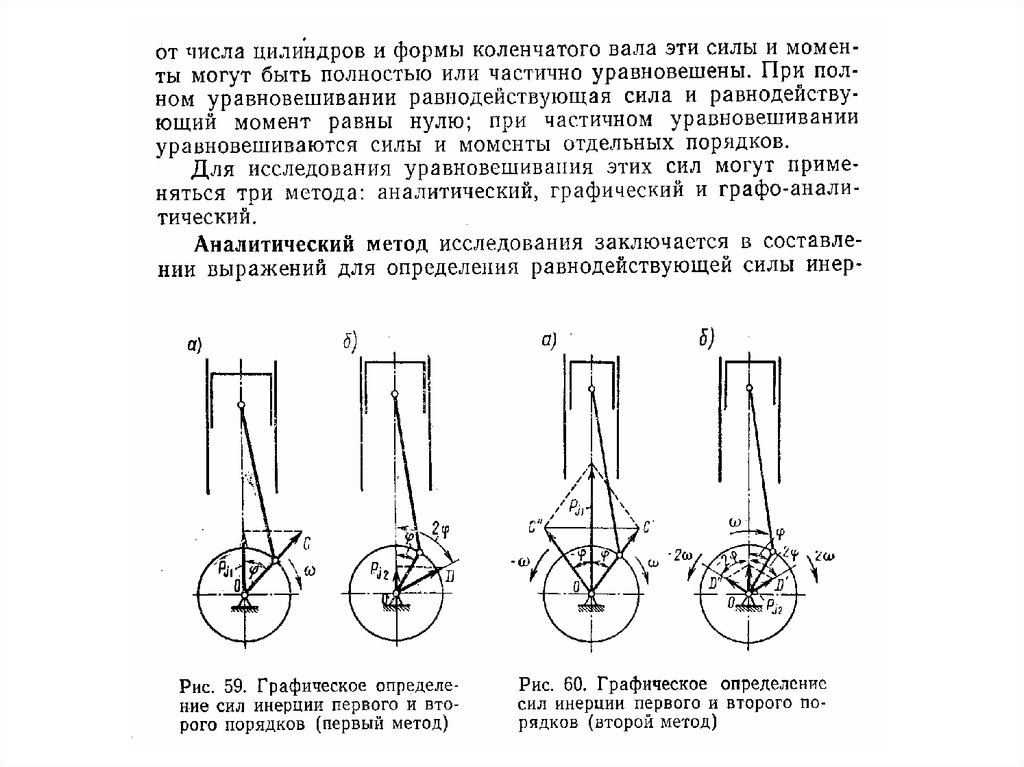
φPj=f (φ)
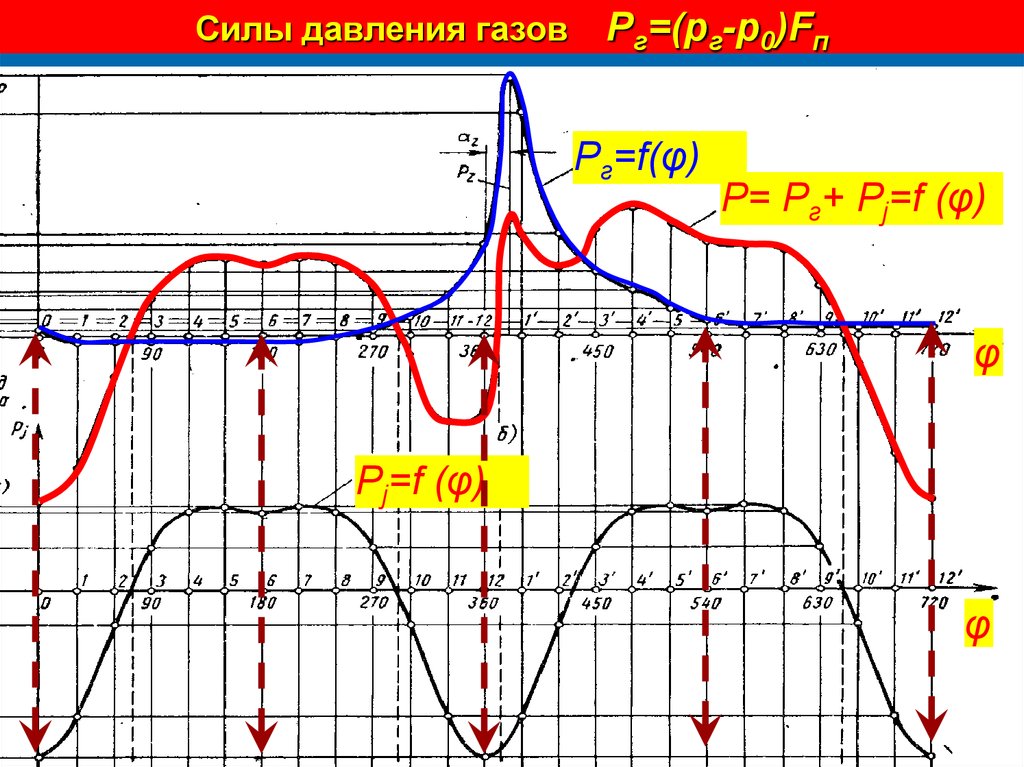
15. Силы давления газов Pг=(pг-p0)Fп
Pг=f(φ)P= Pг+ Pj=f (φ)
φ
Pj=f (φ)
φ
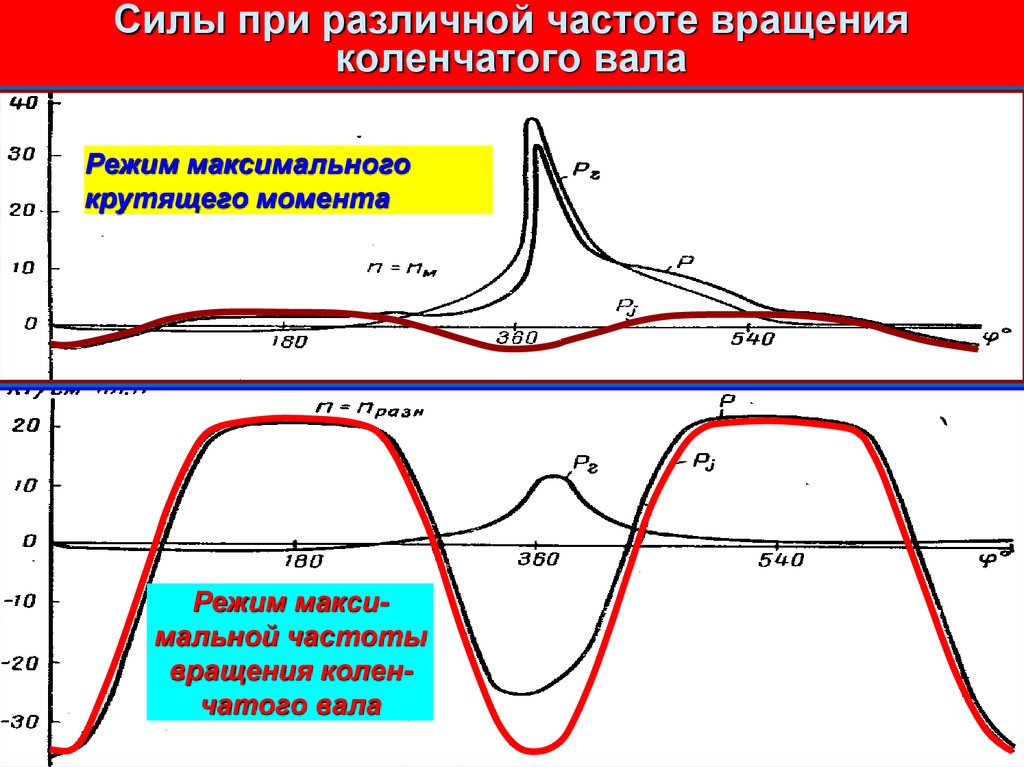
16. Силы при различной частоте вращения коленчатого вала
Режим максимальногокрутящего момента
Режим максимальной частоты
вращения коленчатого вала
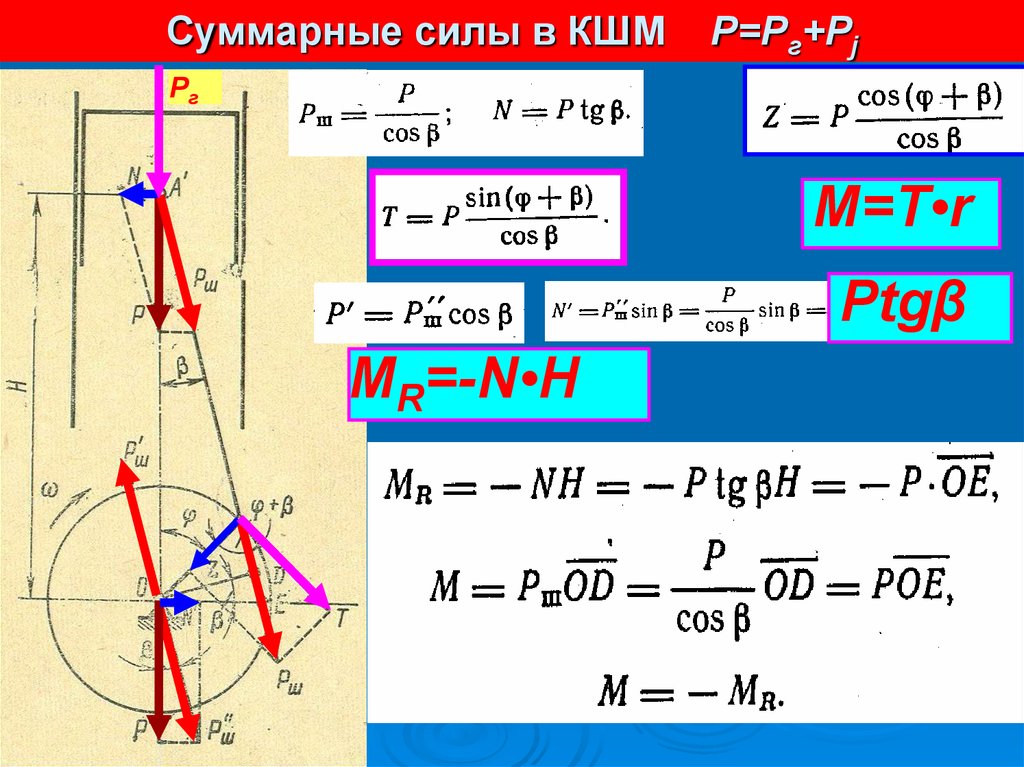
17. Суммарные силы в КШМ Р=Рг+Рj
РгM=T•r
Ptgβ
MR=-N•H
18.
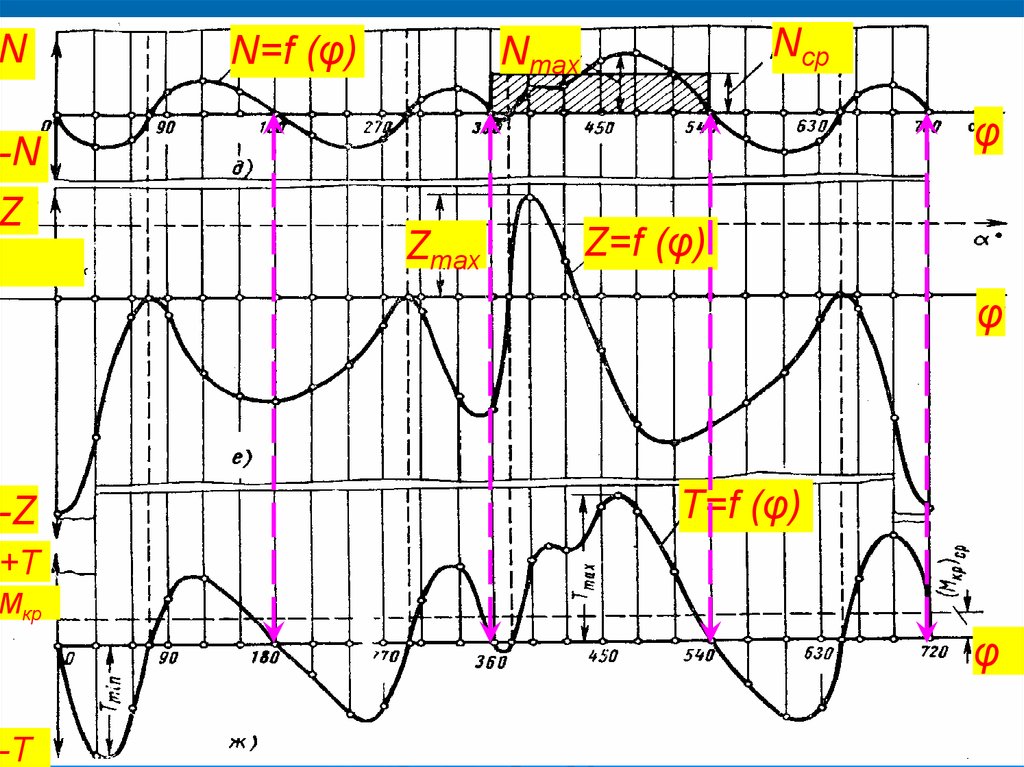
NN=f (φ)
Nср
Nmax
φ
-N
Z
-Z
Zmax
Z=f (φ)
φ
T=f (φ)
+T
Mкр
-T
φ
19.
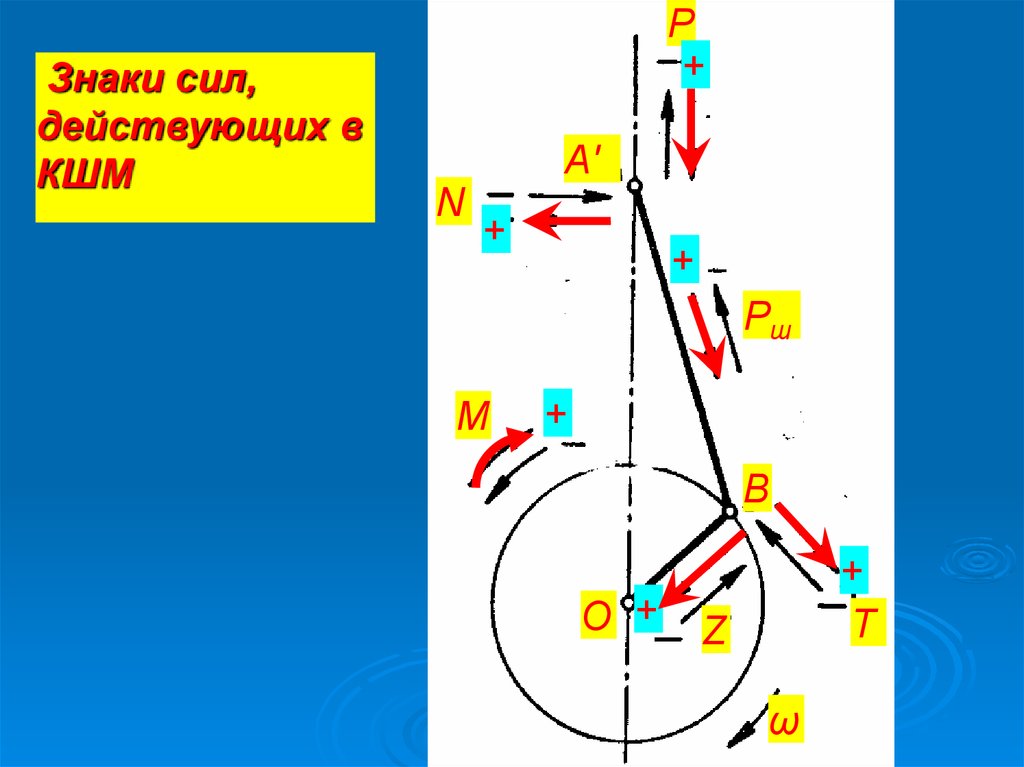
Знаки сил,действующих в
КШМ
P
+
A′
N
+
+
Pш
M
+
B
О +
+
T
Z
ω
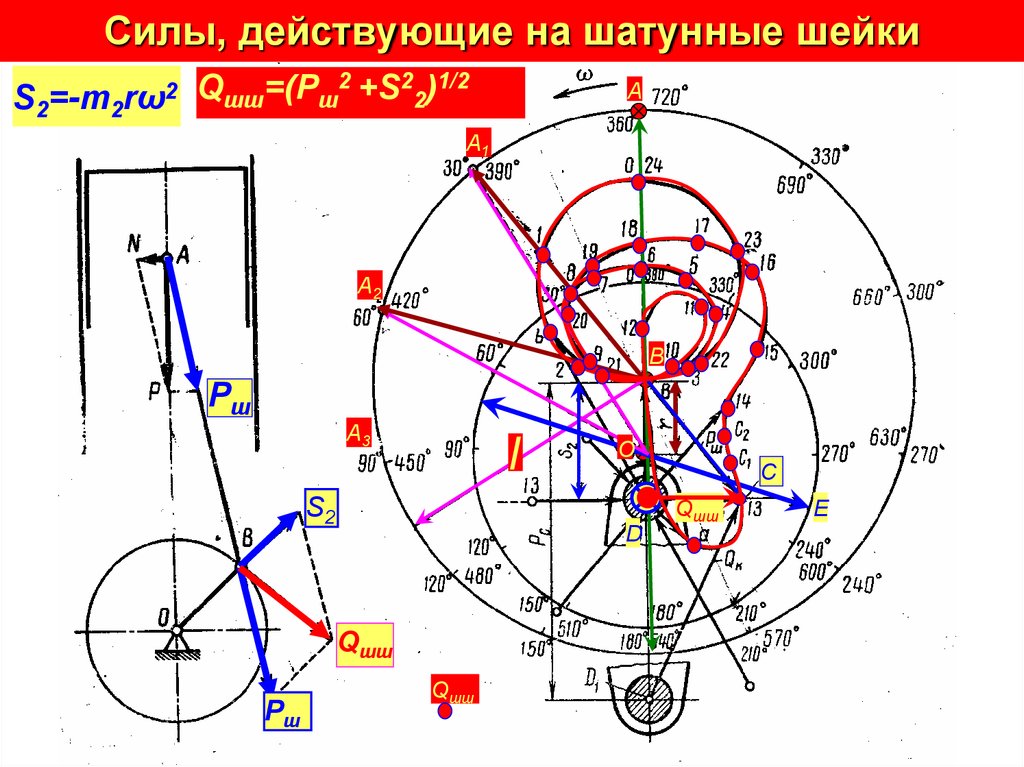
20. Силы, действующие на шатунные шейки
S2=-m2rω2
Qшш=(Рш2 +S22)1/2
A
А1
А2
B
Рш
А3
l
S2
C
Qшш
D
Qшш
Рш
O
Qшш
Е
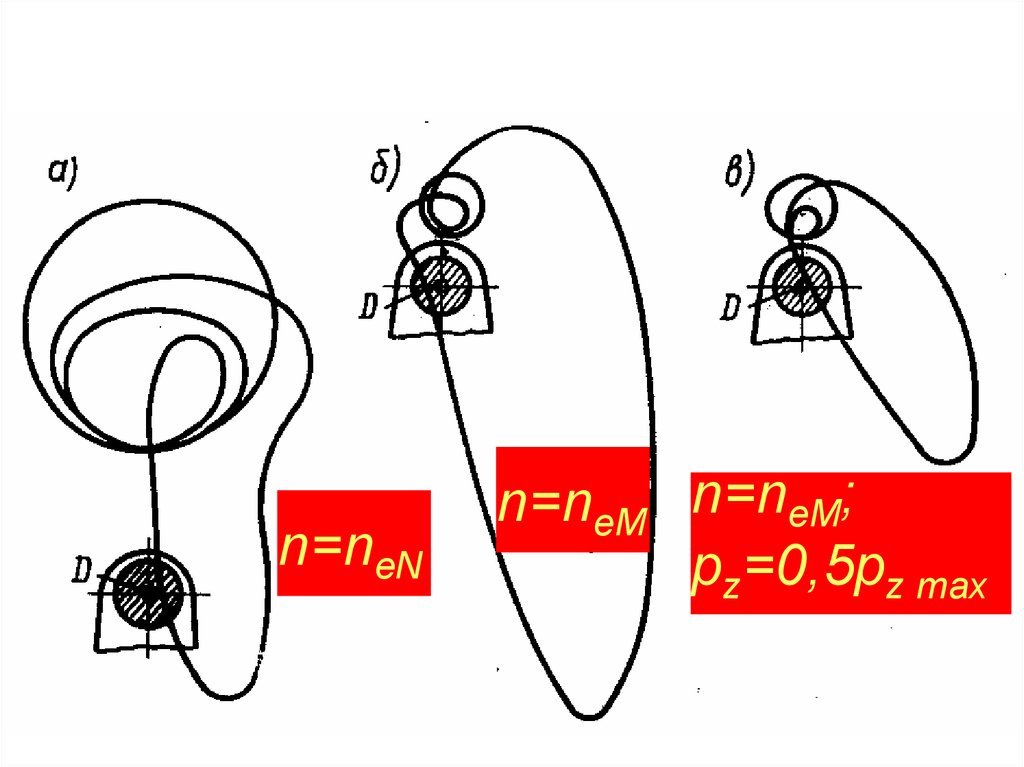
21.
n=neNn=neM n=neM;
pz=0,5pz max
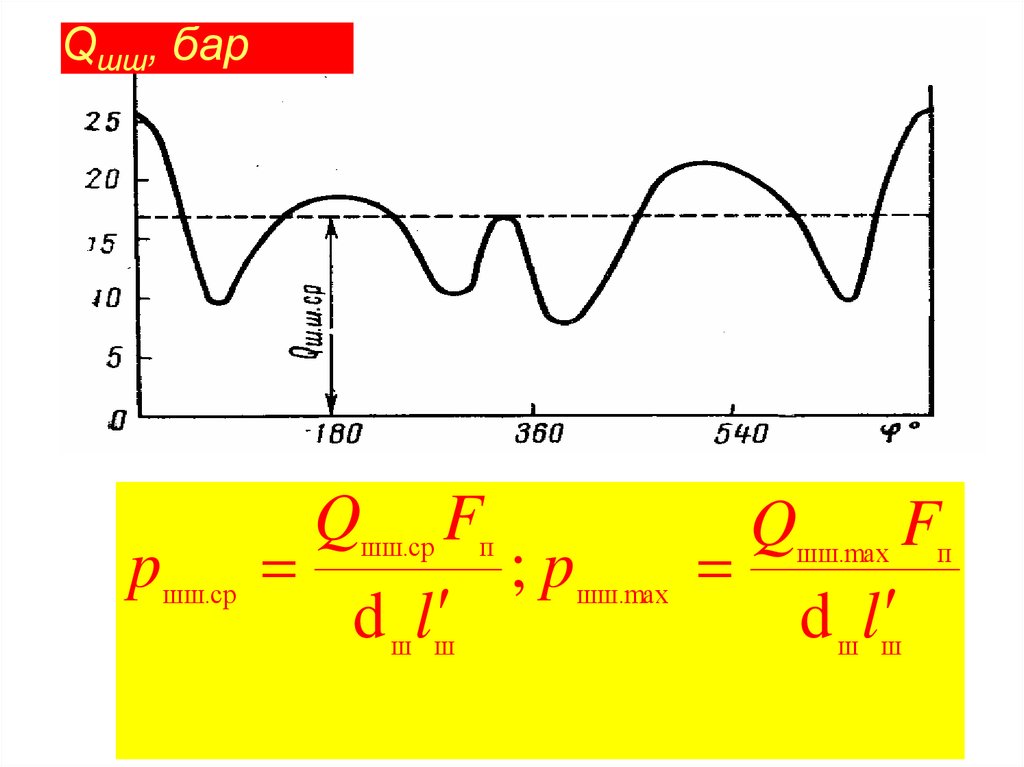
22.
Qшш, барpшш.ср
Qшш.ср Fп
Qшш.max Fп
; pшш.max
d ш lш
d ш lш
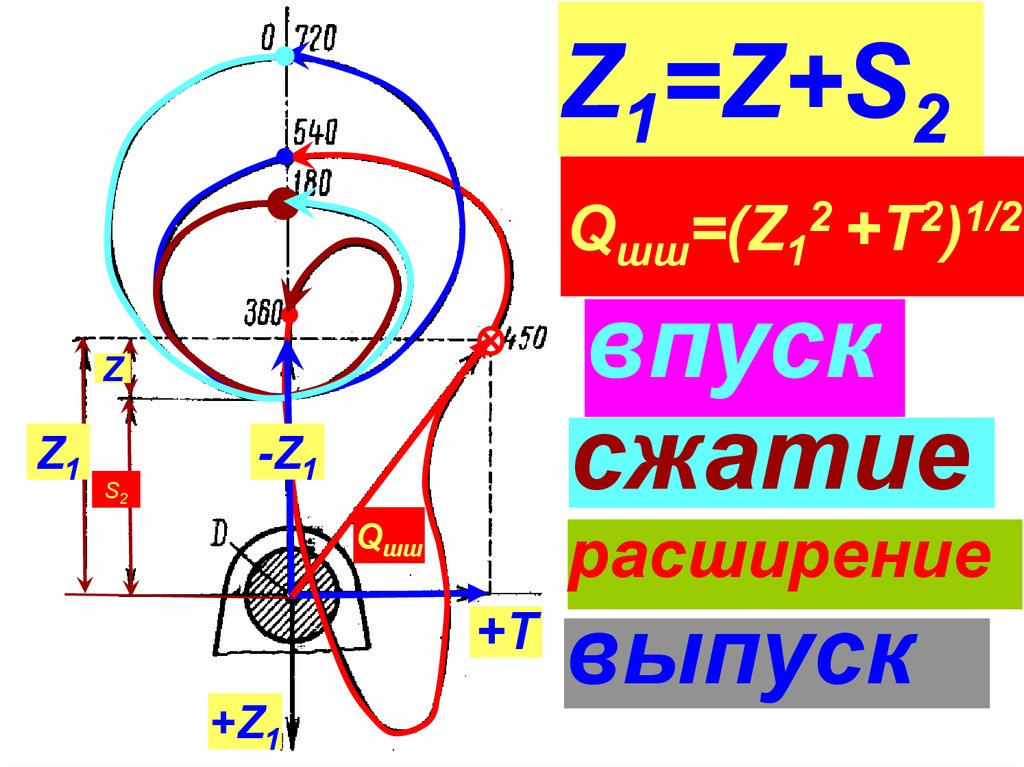
23.
Z1=Z+S2Qшш=(Z1
впуск
сжатие
Z
Z1
S2
-Z1
расширение
Qшш
+T
+Z1
2 +T2)1/2
выпуск
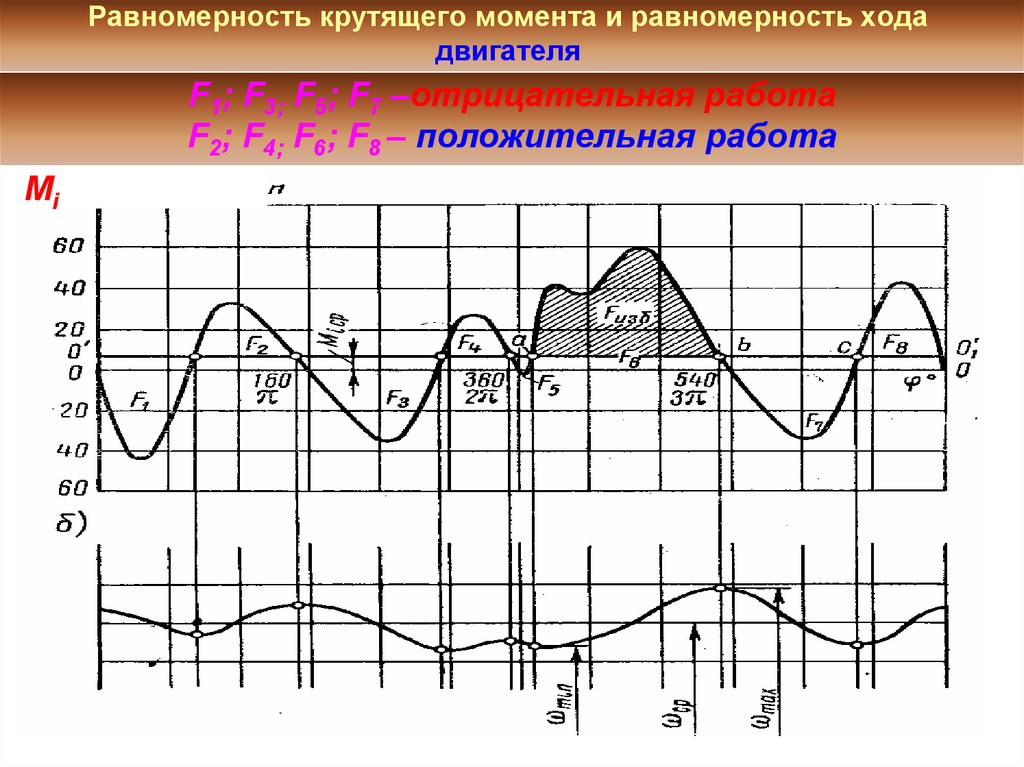
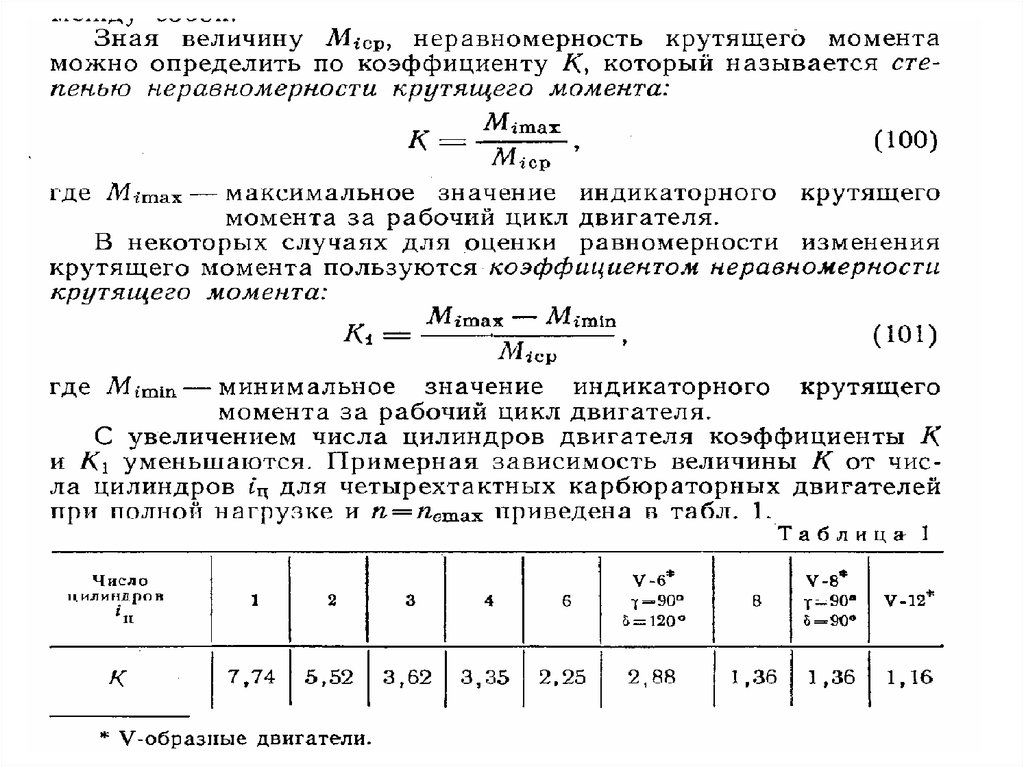
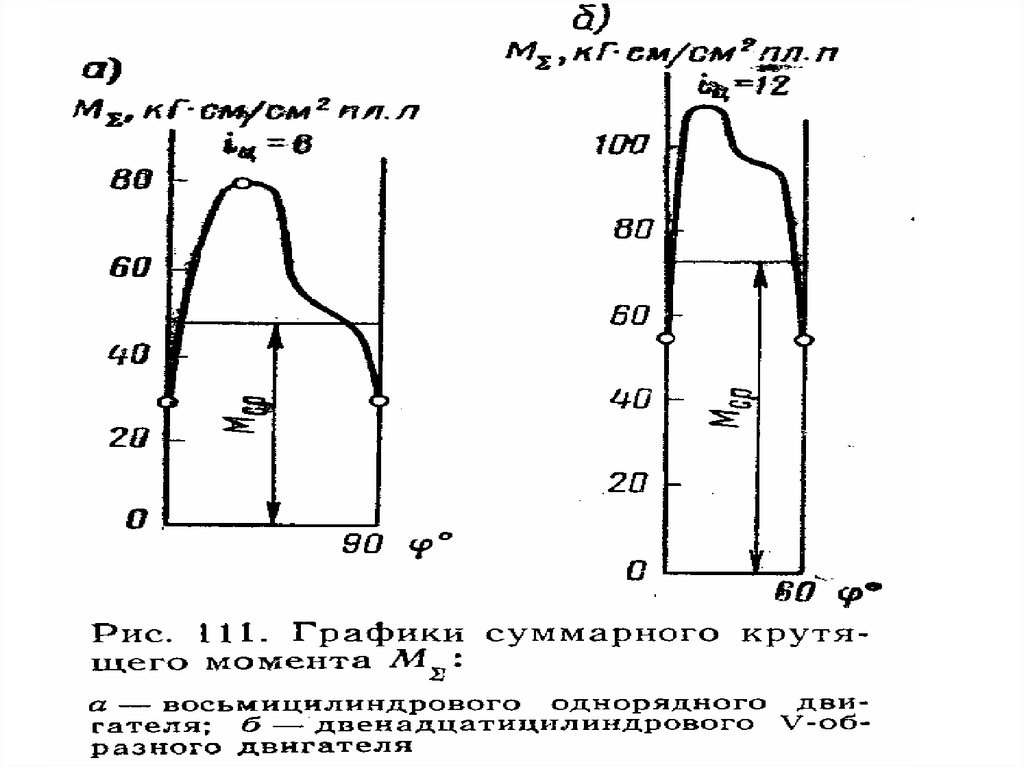
24. Равномерность крутящего момента и равномерность хода двигателя
F1; F3; F5; F7 –отрицательная работаF2; F4; F6; F8 – положительная работа
Мi
Fизб
F2
F1
F4
F3
F5
F8
F6
F7
25.
Условие равновесия моментов Mi=Mсопр+Im(dω/dt)Mсопр – суммарный момент сопротивления;
Im – момент инерции всех движущихся масс,
приведенных к оси коленчатого вала
Полагая Mсопр = const; Mсопр = Miср
Miср = (F/O’O1’)/a1
piFпS=4πMiср
Miср = (piFпri)/2π - 4х тактный
Miср = (piFпri)/π
- 2х тактный
Miср=716,2 Ni/n кгс*м: Ni-л.с. n – мин-1
Miср=974 Ni/n Нм: - Ni-кВт.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
55.
56.
57.
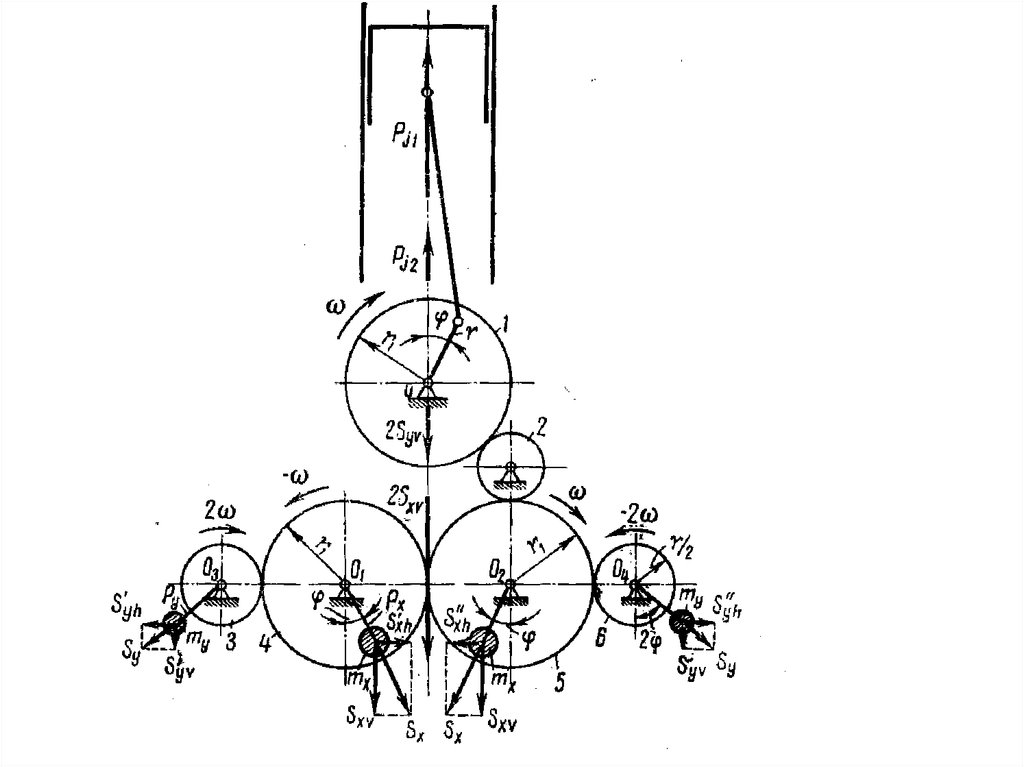
Pj1mΣx
Sh
mΣx
Sv
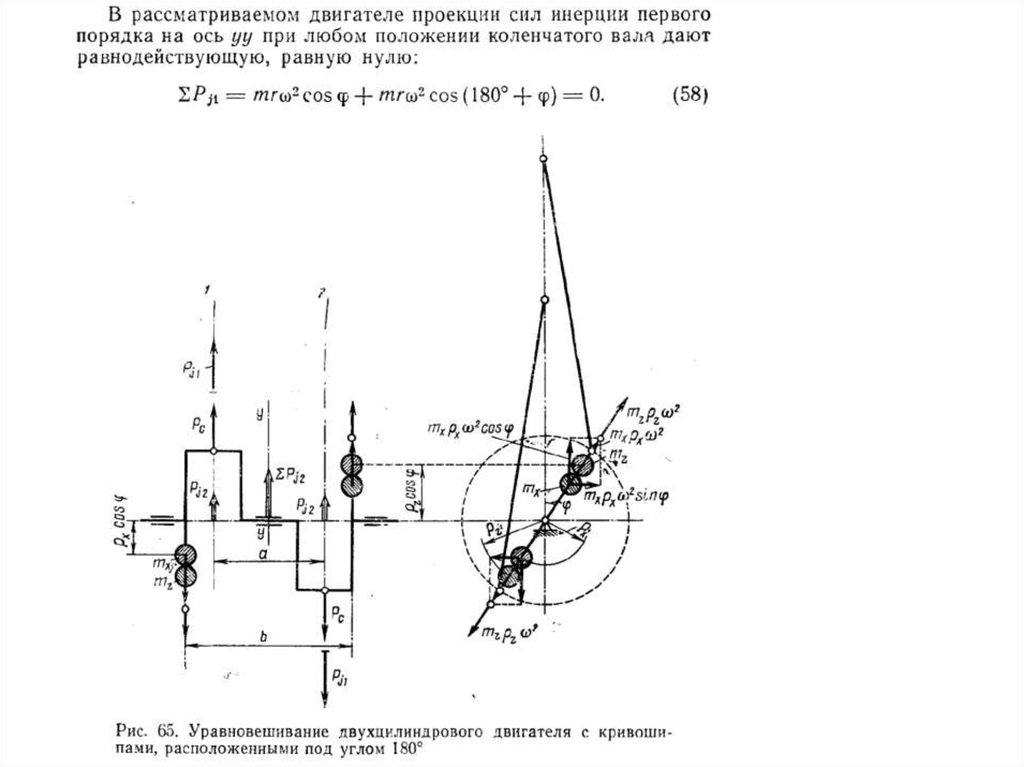
58.
59.
60.
61.
62.
63.
64.
65.
66.
67.
68.
69.
70.
71.
72.
73.
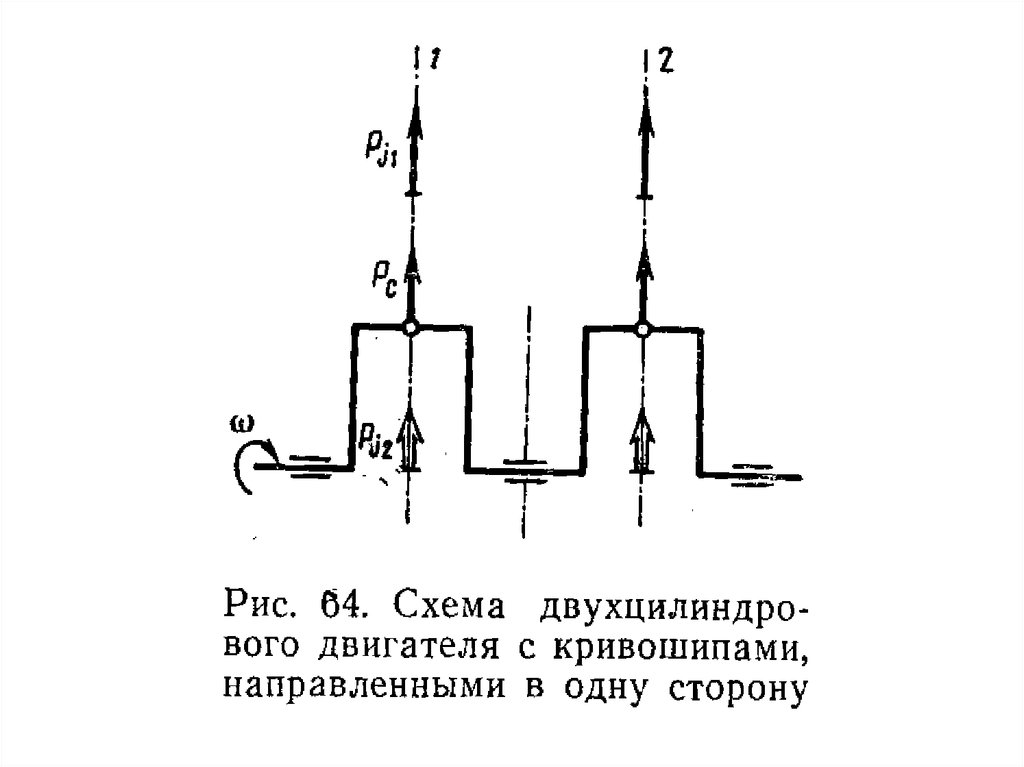
Для 4-х тактных дв. углы между вспышками равны 450 и 2700Для 2-х тактных дв. углы между вспышками равны 90 и 2700
74.
75.
76.
77.
78.
79.
80.
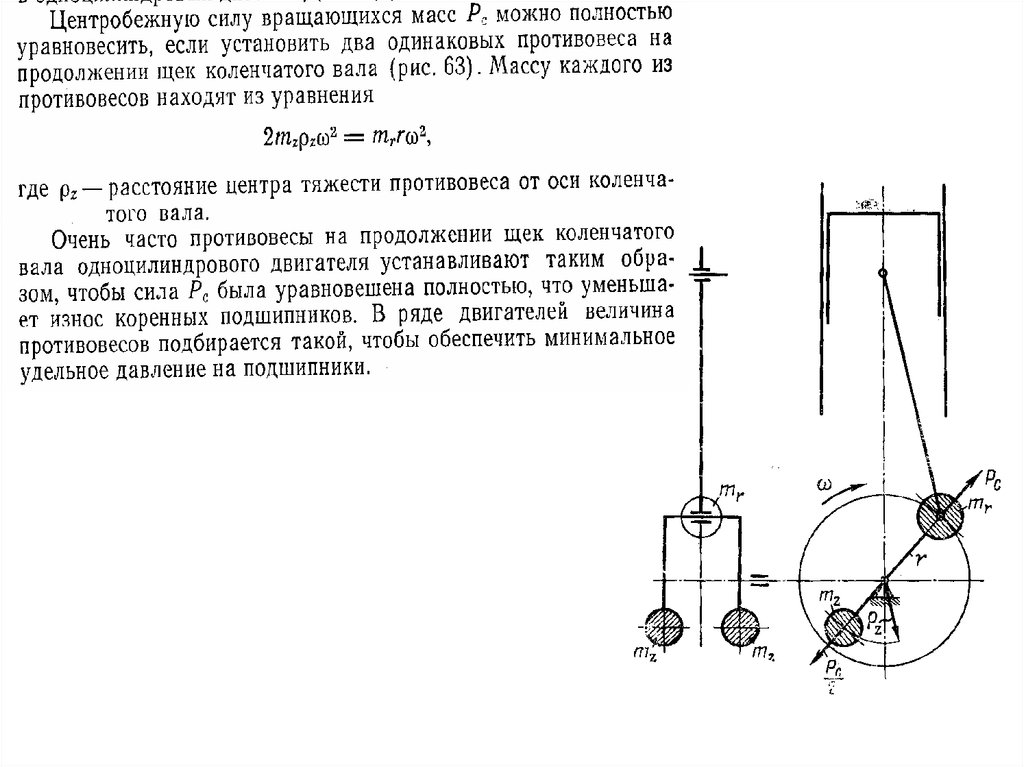
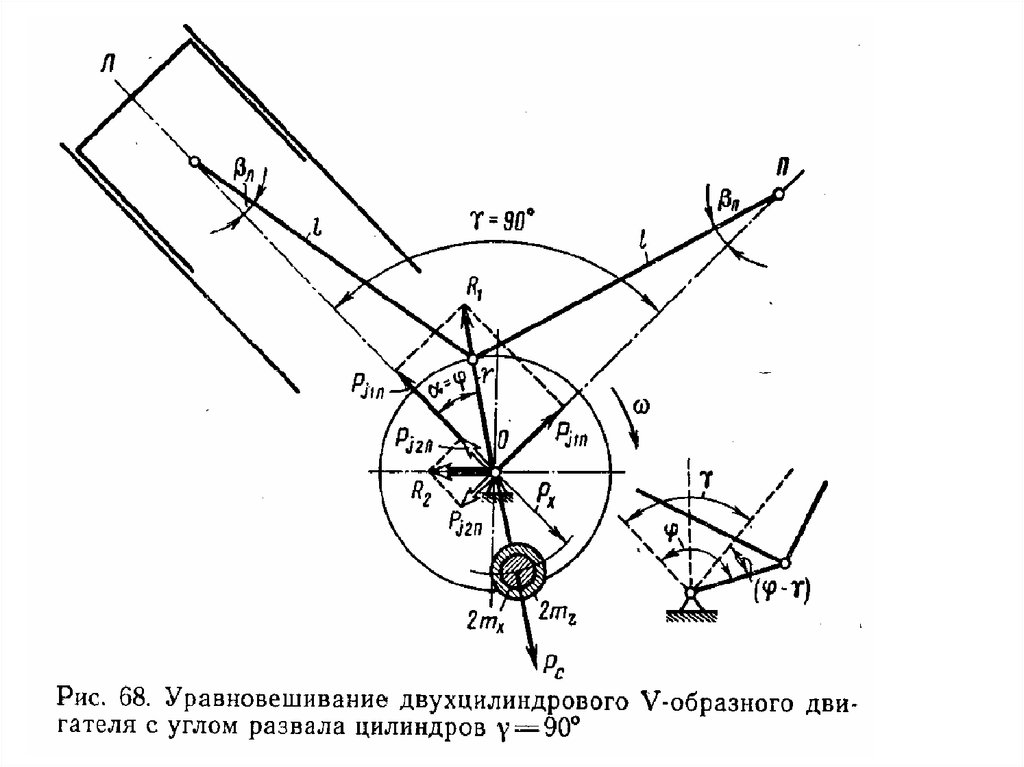
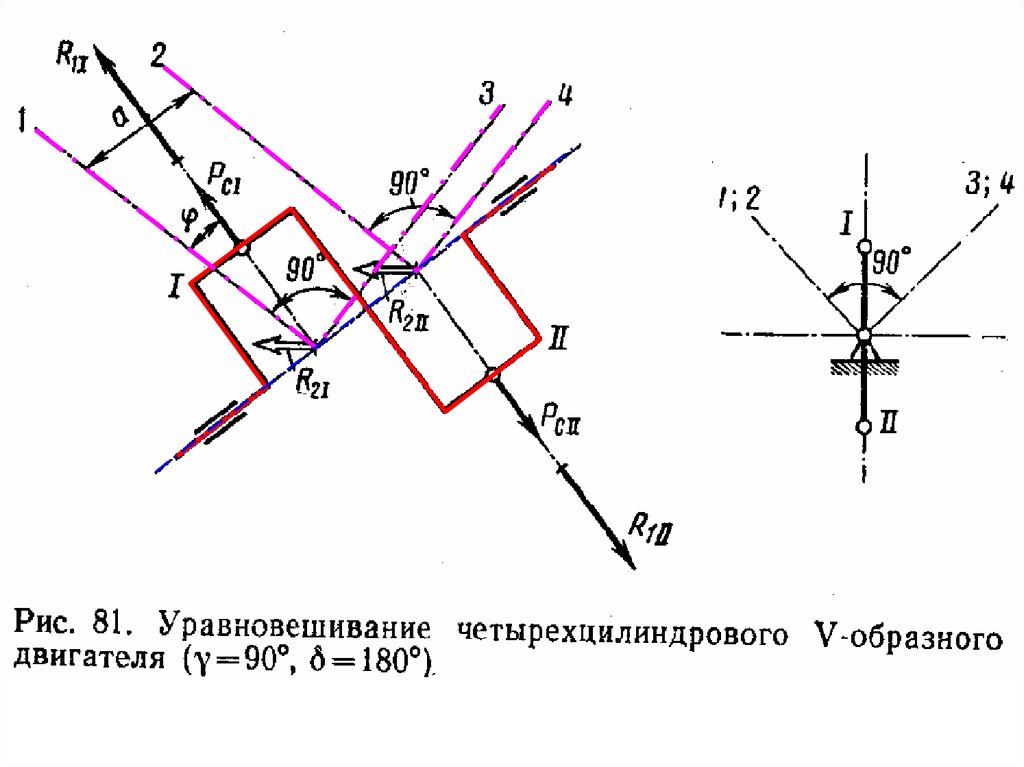
Рс – уравновешивается противовесами, расположенными на продолжениищек коленчатого вала.
Моменты М1; М2 и Мс равны 0
81.
82.
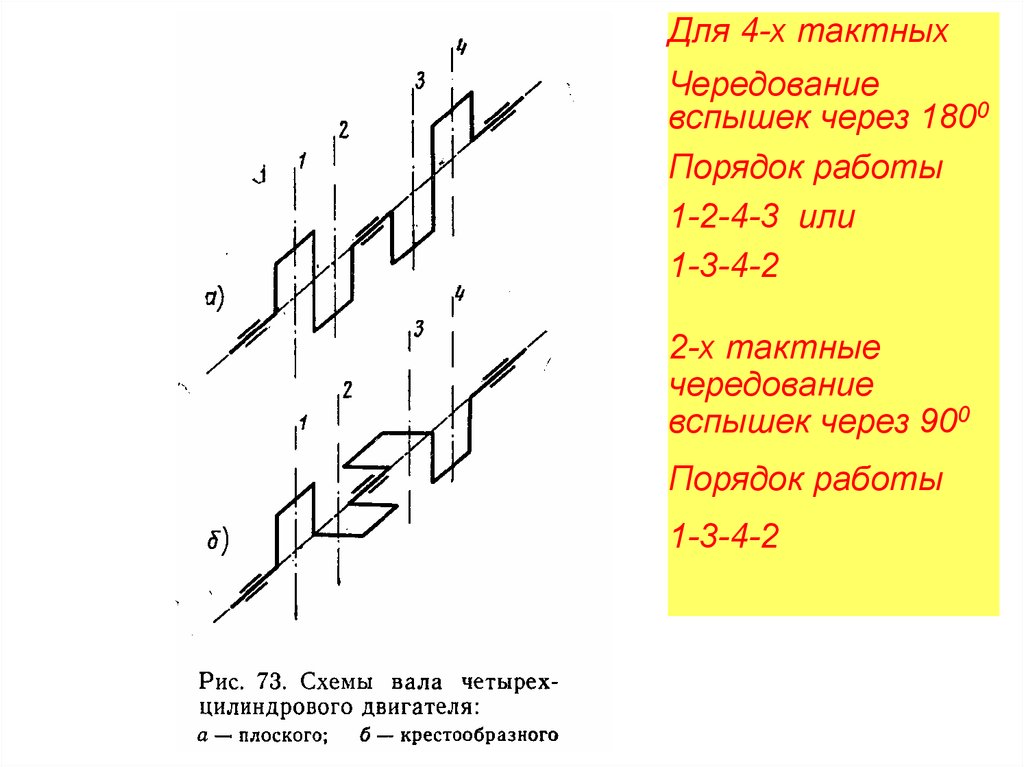
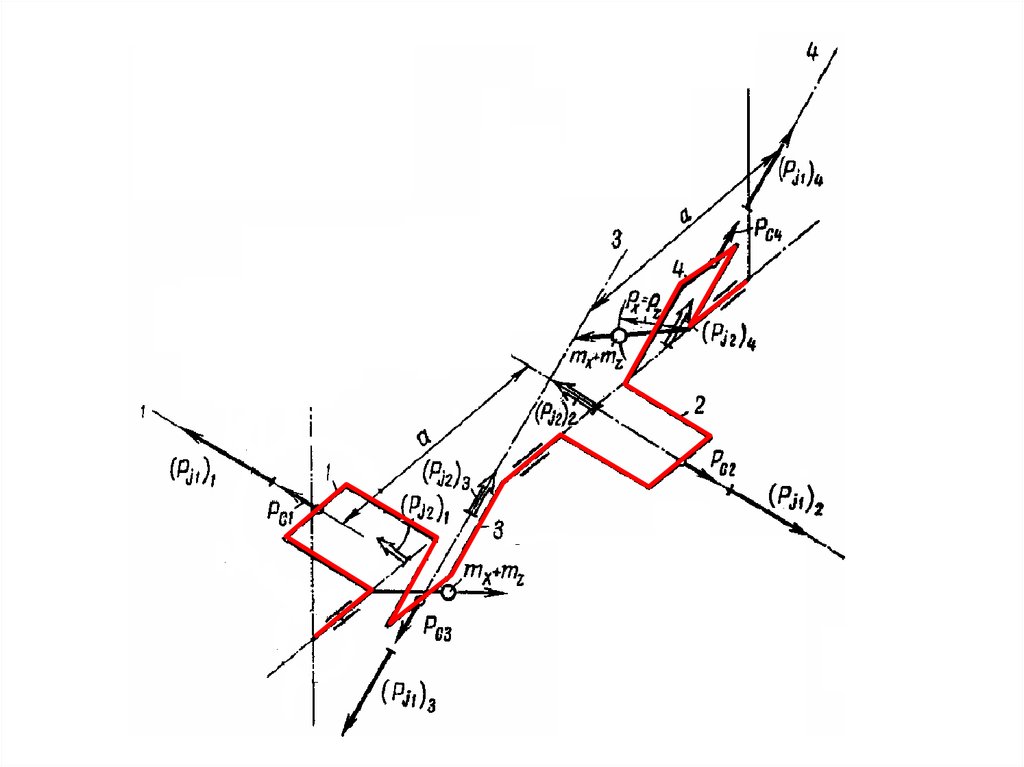
Для 4-х тактныхЧередование
вспышек через 1800
Порядок работы
1-2-4-3 или
1-3-4-2
2-х тактные
чередование
вспышек через 900
Порядок работы
1-3-4-2

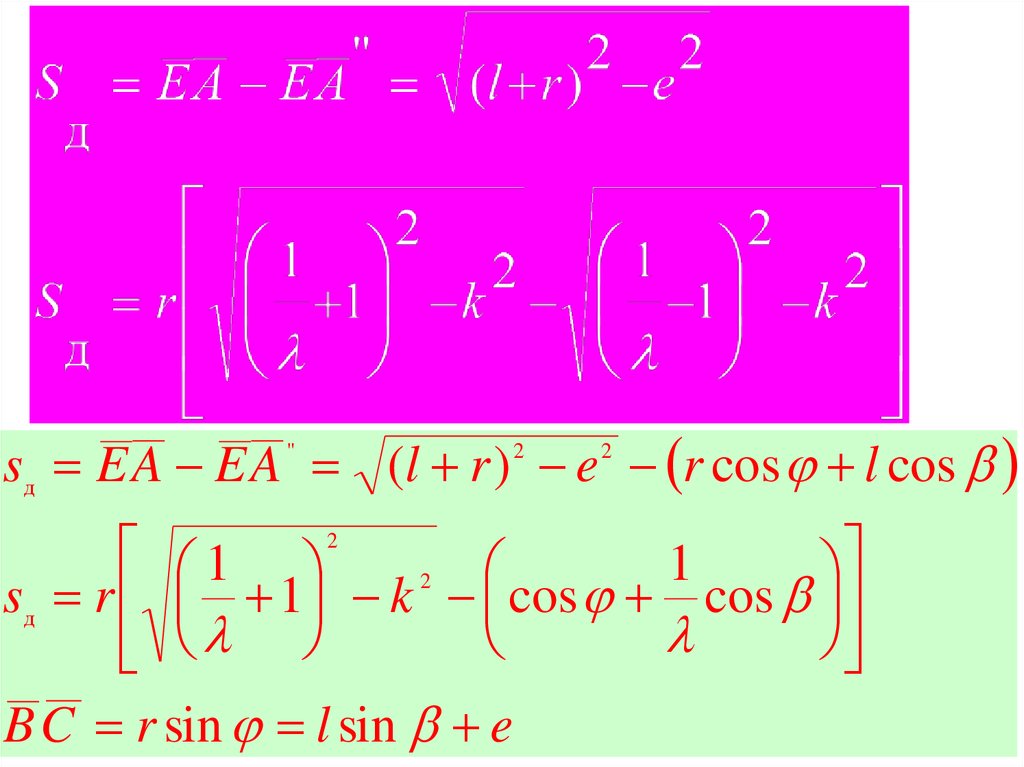































































 finance
finance





