Методика изучения динамики явлений

1. ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

СЧЕТНАЯ ОБРАБОТКА ПОЛУЧЕННЫХ
ДАННЫХ
МЕТОДИКА ИЗУЧЕНИЯ
ДИНАМИКИ ЯВЛЕНИЙ

2.

Одним из важных аспектов анализа различных
явлений представляется оценка их изменений во
времени: за 10-ти или 5-ти летний период, по годам,
месяцам, дням недели, сезонам года.
Анализ таких данных по периодам времени позволяет:
• определить тенденции развития явлений,
• измерить
размеры
произошедших
изменений
и
количественно охарактеризовать направления их развития.

3.

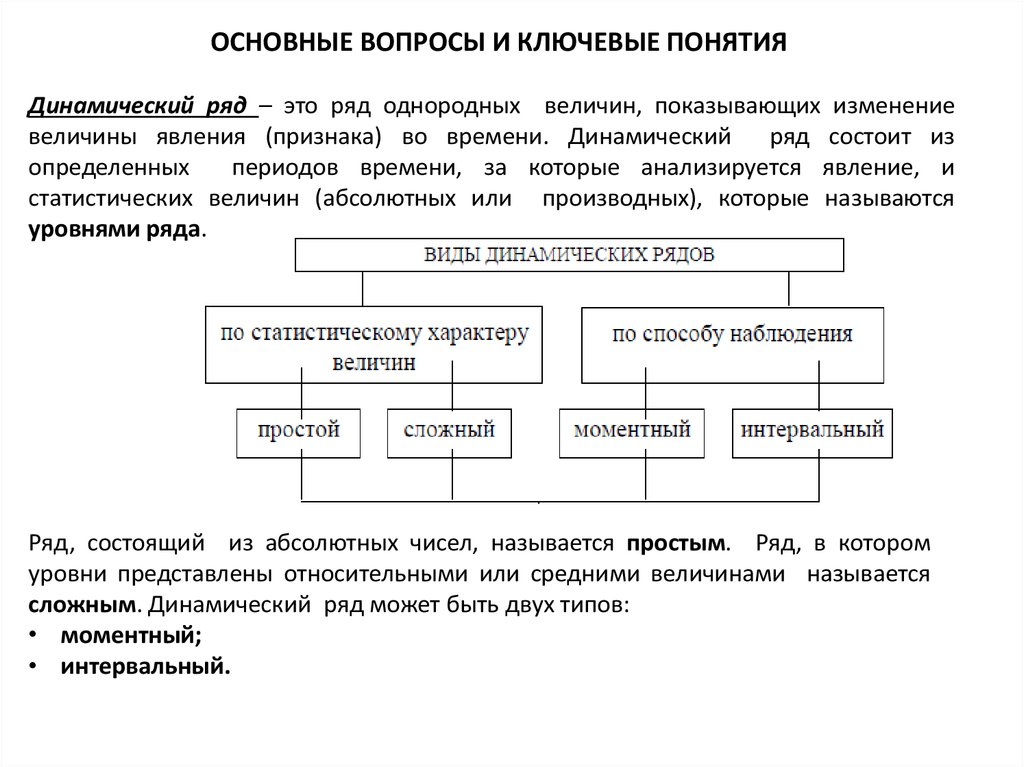
ОСНОВНЫЕ ВОПРОСЫ И КЛЮЧЕВЫЕ ПОНЯТИЯ
Динамический ряд – это ряд однородных величин, показывающих изменение
величины явления (признака) во времени. Динамический ряд состоит из
определенных
периодов времени, за которые анализируется явление, и
статистических величин (абсолютных или производных), которые называются
уровнями ряда.
Ряд, состоящий из абсолютных чисел, называется простым. Ряд, в котором
уровни представлены относительными или средними величинами называется
сложным. Динамический ряд может быть двух типов:
• моментный;
• интервальный.

4.

Моментный ряд представлен числами, характеризующими величину
явления на определенный момент времени, т.е. на определенную дату
(например, данные о численности коек, населения, врачей за ряд лет,
результаты медицинских осмотров и т.д.). Уровни моментного ряда не
подлежат дроблению или
укрупнению, они получены путем
единовременного наблюдения на определенный момент времени (дату).
Интервальный ряд состоит из чисел накопленных за определенный
период времени путем текущего наблюдения (в течение недели, месяца,
года, нескольких лет). Такой ряд можно разделить на более дробные
периоды (год – на кварталы; месяцы – на недели) или укрупнить
(например, по 2, 3 и более лет).
Чем медленнее изменяется явление во времени, тем крупнее могут быть
периоды наблюдения.

5.

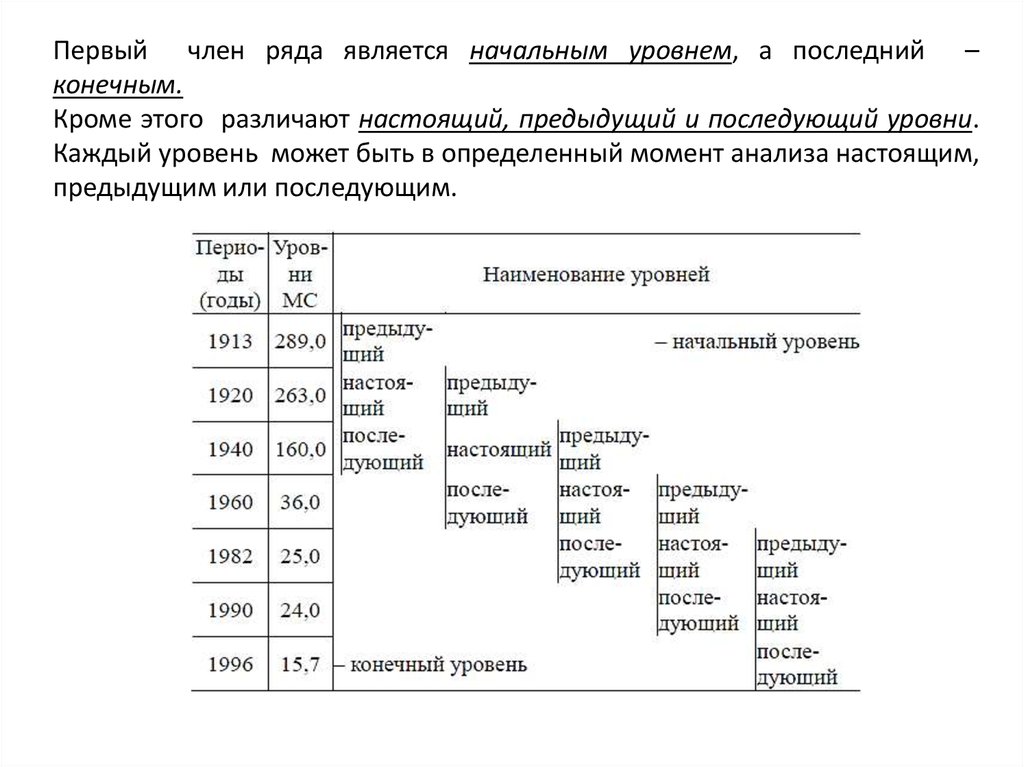
Первый член ряда является начальным уровнем, а последний –
конечным.
Кроме этого различают настоящий, предыдущий и последующий уровни.
Каждый уровень может быть в определенный момент анализа настоящим,
предыдущим или последующим.

6.

Методика изучения динамики явлений

7.

ПОДГОТОВИТЕЛЬНЫЙ ЭТАП
*Определение тенденции изучаемого явления или процесса, т.е. основной
закономерности в изменении уровней ряда. При затруднении
ее
определения рекомендуется произвести выравнивание ряда с помощью
определенного набора способов выравнивания:
• укрупнение периодов (интервалов);
• расчета групповой средней;
• сглаживание ряда при помощи скользящей средней.
*Получение (расчета) показателей динамического ряда:
• абсолютного прироста;
• темпа роста;
• темпа прироста;
• одного процента прироста;
• показателя наглядности.

8.

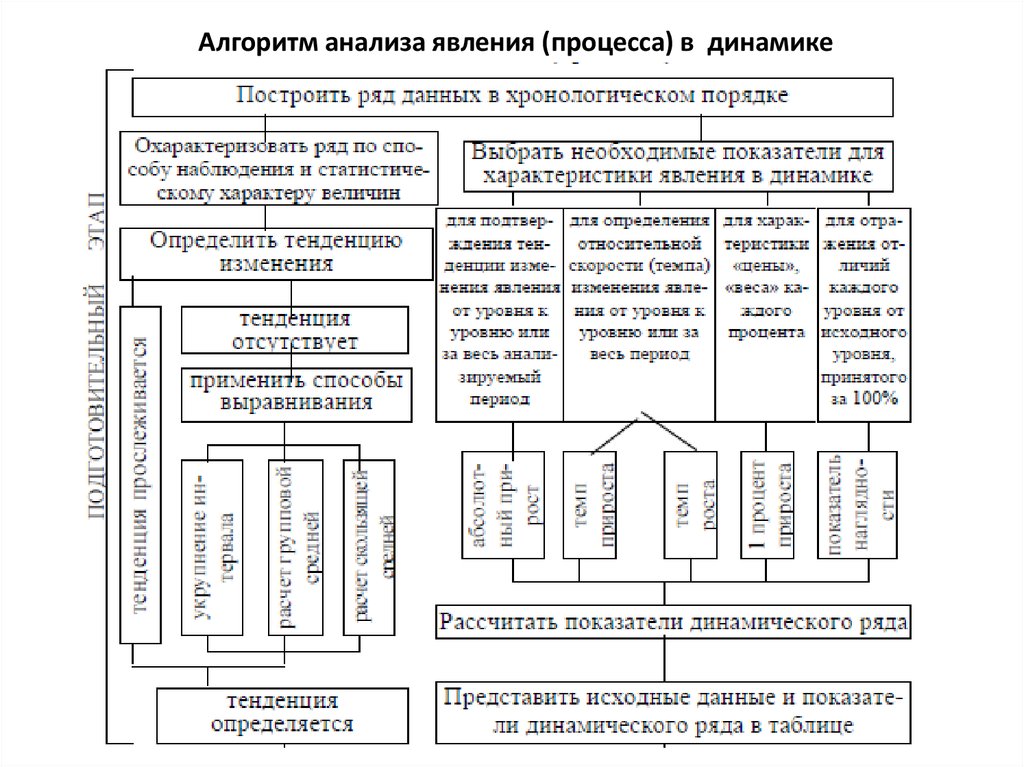
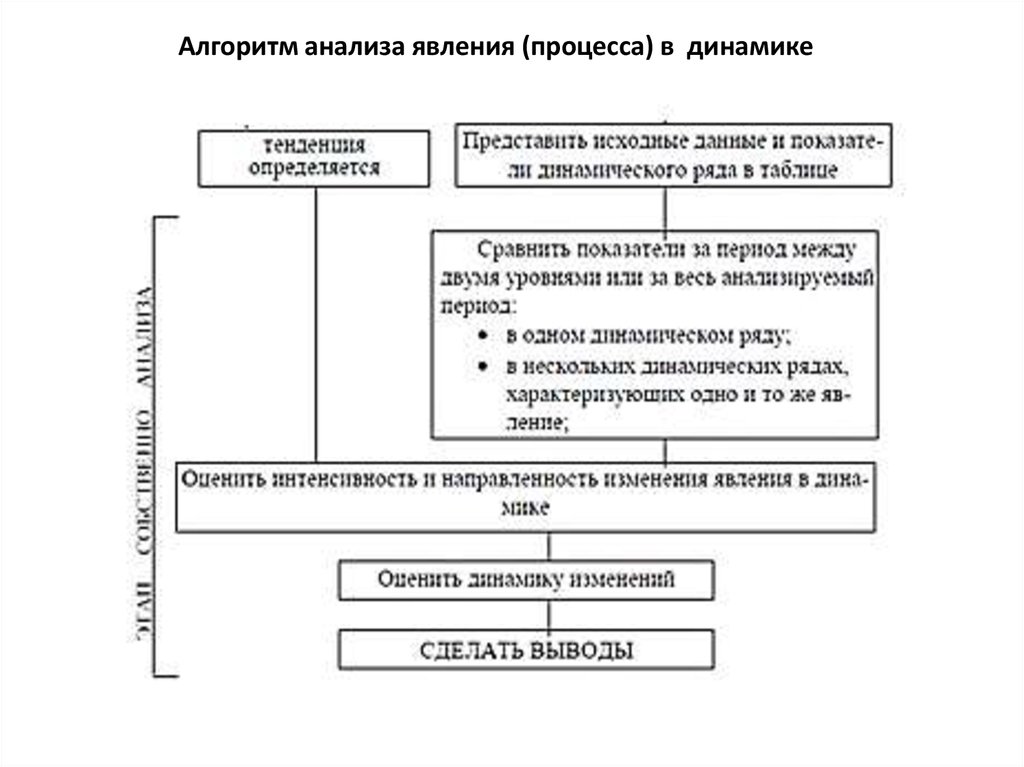
Алгоритм анализа явления (процесса) в динамике

9.

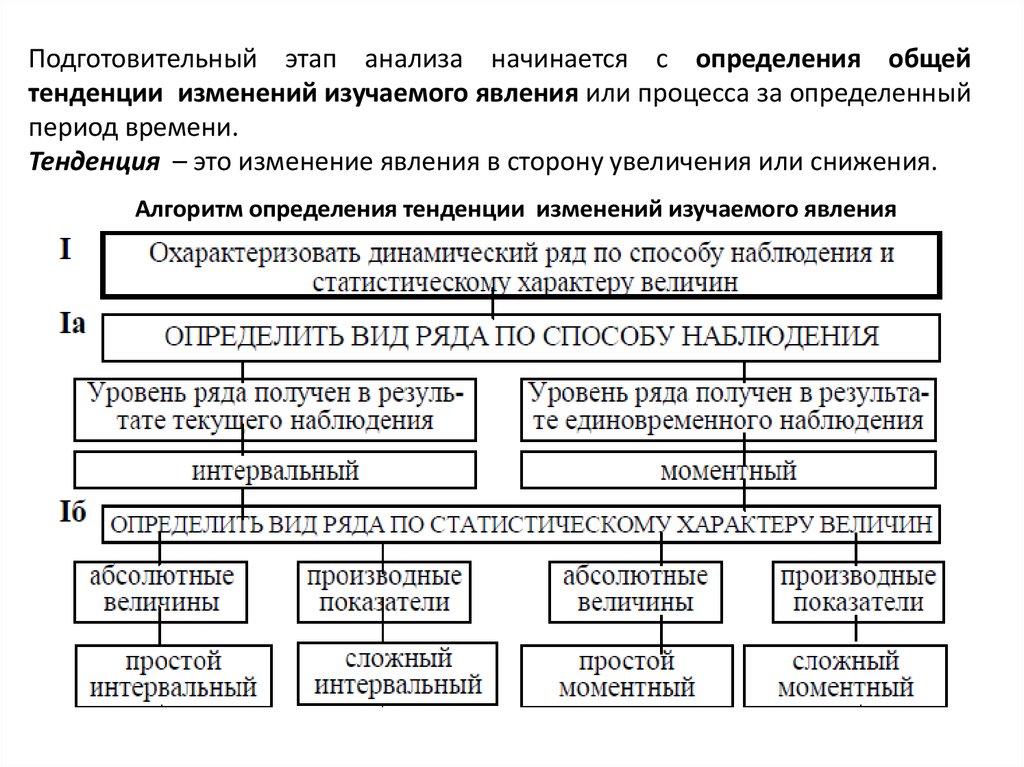
Подготовительный этап анализа начинается с определения общей
тенденции изменений изучаемого явления или процесса за определенный
период времени.
Тенденция – это изменение явления в сторону увеличения или снижения.
Алгоритм определения тенденции изменений изучаемого явления

10.

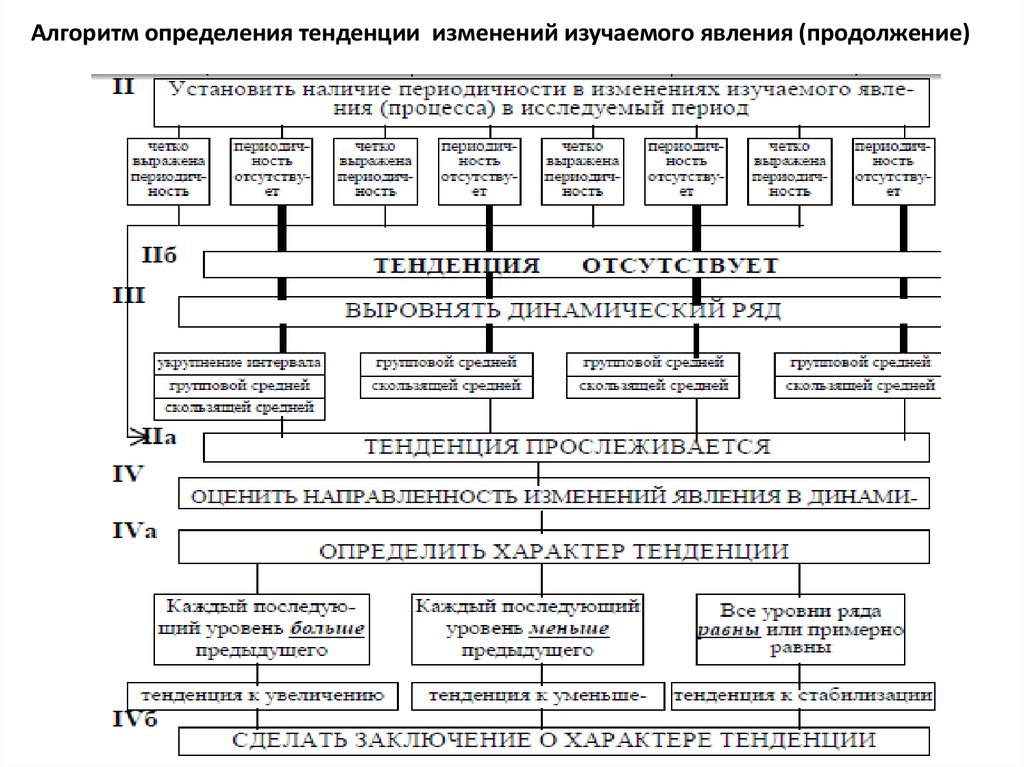
Алгоритм определения тенденции изменений изучаемого явления (продолжение)

11.

Нередко, величина уровней динамического ряда
колеблется, что
затрудняет
возможность проследить основную
закономерность,
свойственную явлению в наблюдаемый период. В таких случаях для
выявления тенденции в изменении явления используется выравнивание
уровней динамического ряда.
Выравнивание
способами:
динамических
рядов
осуществляется
• укрупнение периодов интервала,
• сглаживание ряда при помощи расчета групповой средней,
• скользящей средней.
несколькими

12.

Укрупнение периодов (интервалов) осуществляется путем суммирования чисел за ряд
смежных периодов (2, 3, 4 и т.д.), в зависимости от длины динамического ряда.
Способ укрупнения периодов наиболее часто находит применение при выявлении
основных закономерностей при изучении помесячных изменений явления. Так,
например, помесячные числа заболеваний ангиной в городе А в 2000 г (за год – 433
случая):
январь – 34
июль – 27
февраль – 37
март – 42
апрель – 48
май – 40
июнь – 30
август – 29
сентябрь – 33
октябрь – 41
ноябрь – 39
декабрь – 33
Приведенные числа на первый взгляд создают впечатления об относительно
равномерном распределении случаев заболеваний ангиной по месяцам года.
Однако, если укрупнить периоды динамического ряда и вместо помесячных чисел
взять сезонные, то получится:
зима – 104
весна – 130
лето – 86
осень – 113
В этом случае видна весенне-осенняя тенденция роста заболеваемости ангиной среди
жителей города А.

13.

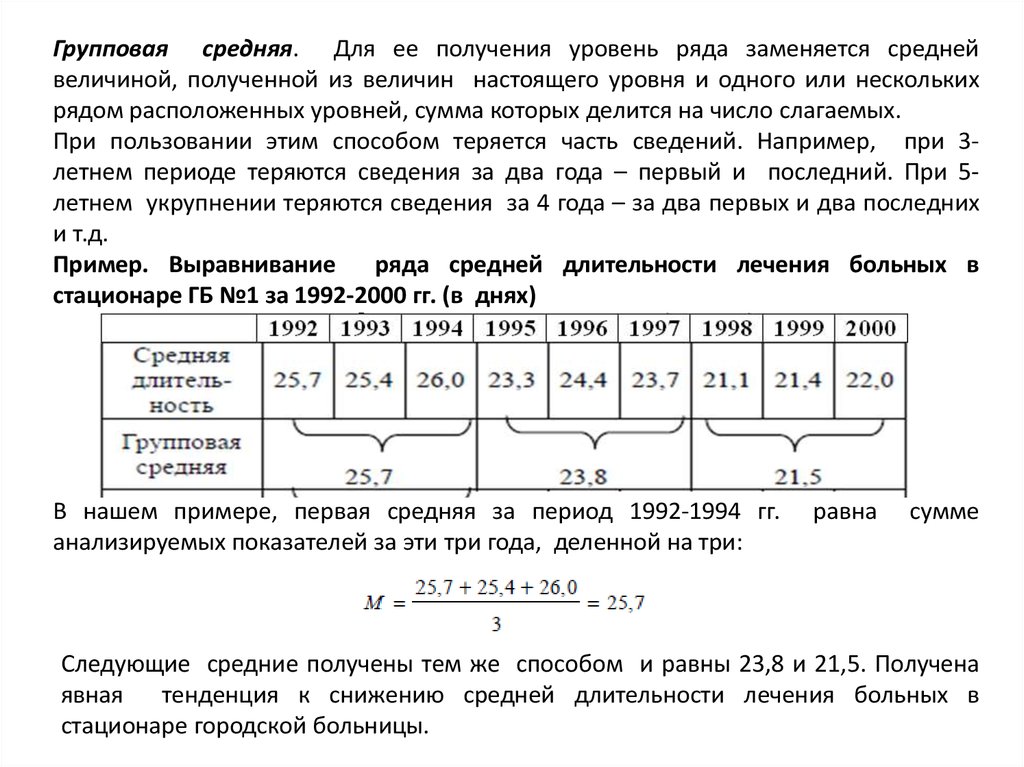
Групповая средняя. Для ее получения уровень ряда заменяется средней
величиной, полученной из величин настоящего уровня и одного или нескольких
рядом расположенных уровней, сумма которых делится на число слагаемых.
При пользовании этим способом теряется часть сведений. Например, при 3летнем периоде теряются сведения за два года – первый и последний. При 5летнем укрупнении теряются сведения за 4 года – за два первых и два последних
и т.д.
Пример. Выравнивание
ряда средней длительности лечения больных в
стационаре ГБ №1 за 1992-2000 гг. (в днях)
В нашем примере, первая средняя за период 1992-1994 гг.
анализируемых показателей за эти три года, деленной на три:
равна
сумме
Следующие средние получены тем же способом и равны 23,8 и 21,5. Получена
явная тенденция к снижению средней длительности лечения больных в
стационаре городской больницы.

14.

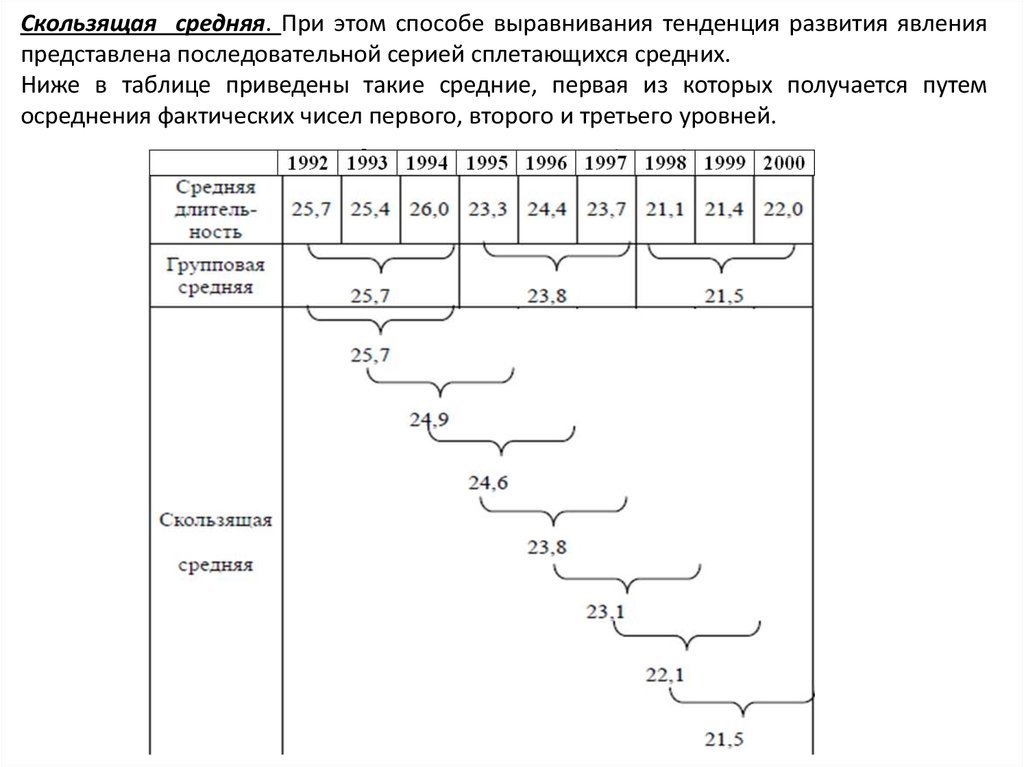
Скользящая средняя. При этом способе выравнивания тенденция развития явления
представлена последовательной серией сплетающихся средних.
Ниже в таблице приведены такие средние, первая из которых получается путем
осреднения фактических чисел первого, второго и третьего уровней.

15.

Полученная скользящая средняя будет относиться ко второму году.
Вторая скользящая средняя получается путем осреднения фактических чисел
за второй, третий и четвертый год. Полученная величина будет относиться к
третьему году.
Аналогично рассчитываются и другие скользящие средние. При указанном
способе также теряется часть сведений.
В таблице приведены два последних рассматриваемых способа выравнивания
динамических рядов. Оба они в приведенном примере показывают явную
тенденцию снижения анализируемого явления. На практике очень часто
бывает ситуация, когда выявляет тенденцию только один из способов.

16.

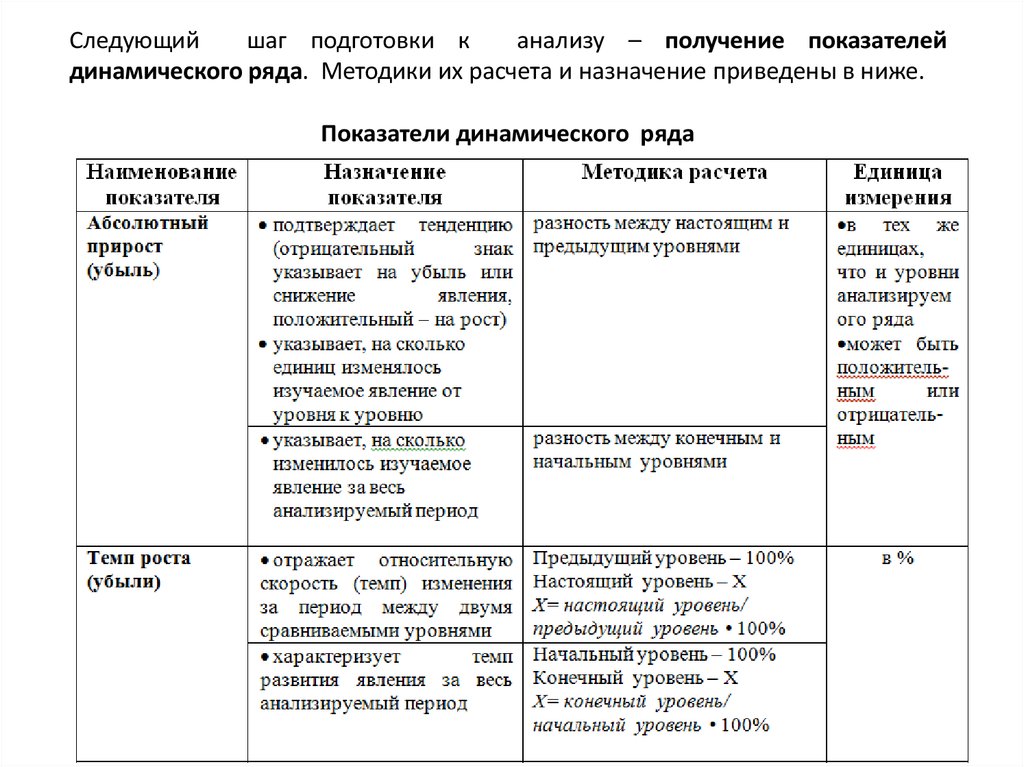
Следующий
шаг подготовки к
анализу – получение показателей
динамического ряда. Методики их расчета и назначение приведены в ниже.
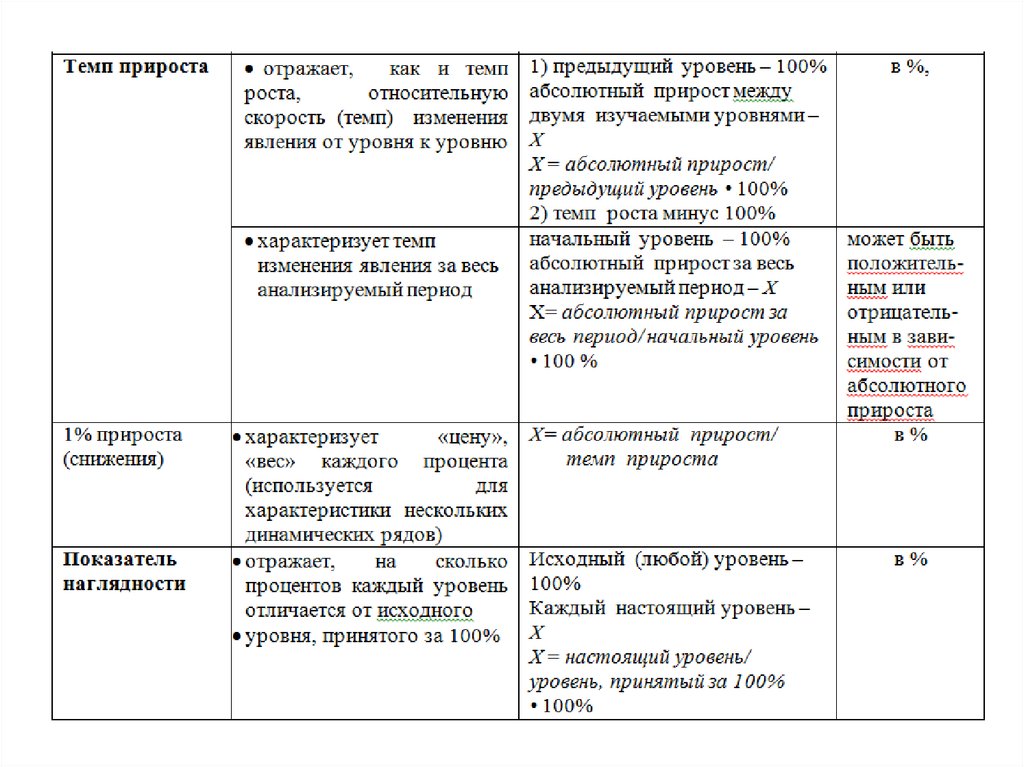
Показатели динамического ряда

17.

18.

ЭТАП СОБСТВЕННО АНАЛИЗА
• сравнении показателей динамического ряда;
• оценке интенсивности и направленности изменения явления;
• объяснении произошедших изменений в динамике.
Методика анализа явления в динамике представляет собой
обязательную последовательность действий и отражена на схеме.

19.

Алгоритм анализа явления (процесса) в динамике

20.

Проанализировать в динамике – это, значит, охарактеризовать явление
по показателям динамики и указать направление изменения.
Необходимо обратить внимание на то, что вычислять весь набор
характеризующих динамический ряд показателей имеет смысл только в
том случае, если явление изучается за длительный период, имеет
существенные колебания, если проводится сравнительный анализ
нескольких динамических рядов.
И наоборот, следует
дифференцированно подходить к выбору
показателей динамики, если явление или процесс изучается за короткий
период времени или с течением времени оно существенно не меняется.
Разберем это на примере.

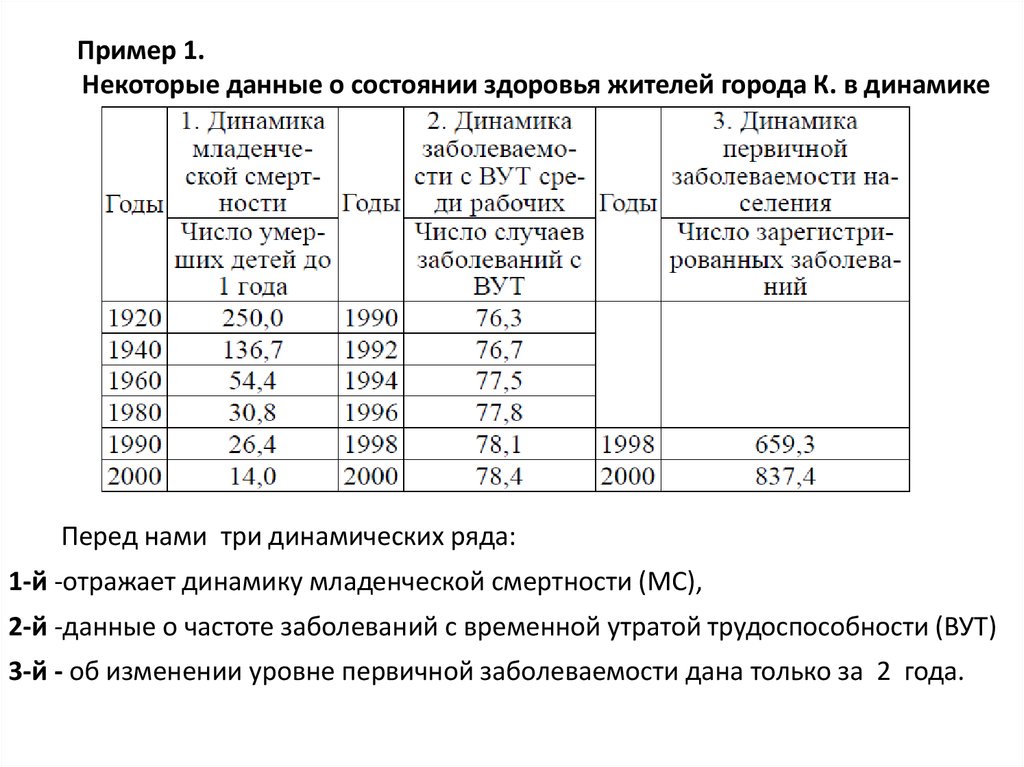
21.

Пример 1.
Некоторые данные о состоянии здоровья жителей города К. в динамике
Перед нами три динамических ряда:
1-й -отражает динамику младенческой смертности (МС),
2-й -данные о частоте заболеваний с временной утратой трудоспособности (ВУТ)
3-й - об изменении уровне первичной заболеваемости дана только за 2 года.

22.

Для анализа 1-го ряда можно использовать весь набор показателей
динамики, поскольку в нем заметны значительные колебания уровней.
Во 2-ом ряду изменения частоты случаев незначительны. Поэтому
использовать для анализа этого явления показатели темпа роста или
прироста не целесообразно. В этом случае достаточно применить показатели
абсолютного прироста и наглядности по отношению к любому условно
принятому основанию за 100%.
3-й ряд отличается более коротким периодом (2 года). В этом примере тоже
нет необходимости анализировать изучаемое явление с помощью всех
показателей динамики. Достаточно использовать два показателя, так как в
этом случае эти показатели не с чем сравнивать.

23.

Анализ 1-го ряда
1. По величине абсолютного прироста можно сделать заключение о
направлении и об интенсивности изменений МС.
1.1. Так, в городе К с 1913 года по 2000 гг отмечалась явная тенденция к
снижению МС (все показатели абсолютного прироста имеют
отрицательное значение). За весь анализируемый период смертность
детей первого года жизни снизилась на 274,3 случая в каждой 1000
родившихся живыми.
1.2. Самое заметное снижение МС наблюдалось с 1940 по 1960 гг.
Показатель абсолютного прироста (АП) за этот период равнялся 124
случаям на 1000 родившихся живыми. Далее следует выделить период с
1920 по 1940 гг. (показатель АП равен -103,0). Практически без изменений
МС оставалась с 1980 по 1990 гг. (АП равен -1,0). В последний
анализируемый период, т.е. 1990-2000 гг., АП составил – -9,3 случая смерти
детей первого года жизни на каждую 1000 родившихся живыми.

24.

2. Сравнивая показатели темпа роста и темпа прироста, нетрудно заметить,
что темп прироста равен темпу роста минус 100%. Оба эти показателя дают
представление об относительной скорости уменьшения МС за изучаемый
период.
Учитывая, что по статистической природе оба показателя представляют
собой показатели наглядности, для анализа можно использовать один из
них. Остановимся на темпе прироста. Анализируя эти показатели можно
заметить, что с 1920 по 1940, с 1960 по 1980 и с 1990 по 2000 годы темп
прироста МС был примерно одинаков и снижение находилось в пределах
30-40%. Следует обратить внимание на периоды 1940-1960 гг. и 1980-1990 гг.
В первый из них отмечается самая большая скорость снижения (показатель
равен –77,5%), во второй – самая незначительная убыль (показатель равен –
4,0%). За весь изучаемый период МС снизилась на 95%. Аналогичное
заключение можно сделать по показателям темпа роста.
3. Оценим показатель наглядности. За 100% приняты уровни МС 1913 года.
По сравнению с этим годом отмечается снижение МС во все анализируемые
годы. Особенно заметны различия уже с 1940 года (снижение на 45%). В
1960 году смертность детей первого года жизни снизилась почти на 87%. Во
все остальные периоды, начиная с 1980 г., она снизилась более чем на 90%.

25.

Пример 2.
Динамика числа коек в медицинских учреждениях города Н.
Анализ
1. Показатели темпа роста и темпа прироста в ГБ №1 и ГБ №2 одинаковы, хотя
показатели абсолютного уровня и абсолютного прироста в ГБ №1 гораздо выше
показателей в ГБ №2. В ГБ №1 33,33% темпа прироста получены за счет 70 вновь
открытых коек, а в ГБ №2 – за счет 30 (см. показатель абсолютного прироста в
указанных больницах). Точно также при низком абсолютном уровне коек в ГБ №3 а,
следовательно, и низком абсолютном приросте получились более высокие показатели
темпа роста и темпа прироста, чем при высоком абсолютном уровне, фактически
большем абсолютном приросте коек в ГБ №1, где получились более низкие показатели
темпа роста и темпа прироста.

26.

2. Показатели темпа роста и темпа прироста в ГБ №3 и ГБ №4 различаются
по величине, хотя показатели абсолютного прироста равны между собой в
обоих ГБ. Это является результатом разных по величине показателей
абсолютного уровня коек за 1999 год (70 в ГБ №3 и 230 в ГБ №4).
Приведенный пример показывает, что применение показателей темпа роста
и темпа прироста всегда следует сопровождать анализом и других двух
показателей: абсолютного уровня коек за 1999 год (70 в ГБ №3 и 230 в ГБ
№4). Приведенный пример показывает, что применение показателей темпа
роста и темпа прироста всегда следует сопровождать анализом и других
двух показателей: абсолютного уровня и абсолютного прироста.