Similar presentations:
Механіка грунтів
1. Лекція №5
МЕХАНІКА ГРУНТІВГрунт як деформоване тверде тіло.
Напружено-деформований стан
однорідного та шаруватого
грунтового масиву
2.
1.Грунт як деформоване твердетіло
1.1. Про механіку ґрунтів
В розділі “Грунтознавство” вивчали
походження різних ґрунтів, їх фізичні і
будівельні властивості.
В
розділі
“Механіка
ґрунтів”
вивчаються механічні властивості грунтів,
методи
визначення
напружень
і
деформацій в грунтових масивах, а також
методи розрахунку ґрунтових масивів на
міцність та стійкість.
Механічними
прийнято
називати
властивості, які характеризують поведінку
грунту під дією навантаження.
3. 1.2. Поняття про навантаження, напруження, переміщення та деформації. Навантаження
На ґрунтовий масив діють тривалі ікороткочасні навантаження.
Тривалі (тривалістю від 102с до 102
років) :
• від власної ваги розташованого вище
ґрунту;
• від ваги споруд, які опираються на
ґрунт.
4.
Короткочасні (тривалістю від 10-3сдо 10 с):
• від проїзду
літаків;
автомобілів,
поїздів,
• від вібрації двигунів, генераторів,
машин в приміщеннях.
5. Приклади навантаження
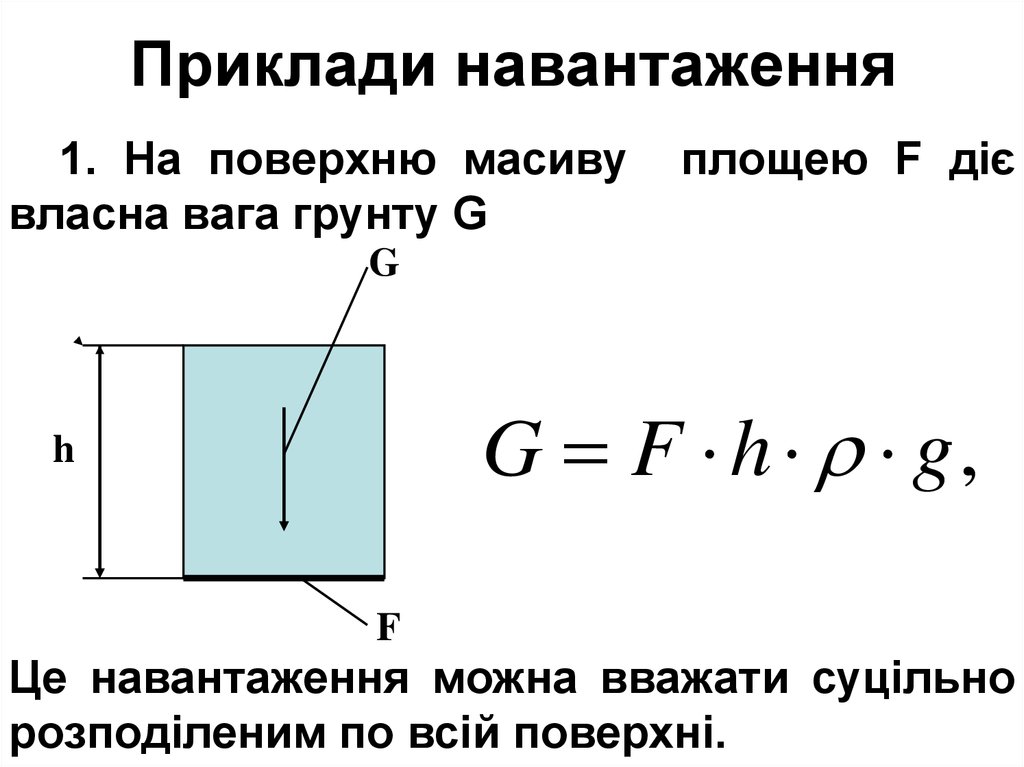
1. На поверхню масивувласна вага грунту G
площею F діє
G
G F h g,
h
F
Це навантаження можна вважати суцільно
розподіленим по всій поверхні.
6.
Таким чином на масив, розміщений підшаром грунту товщиною h з щільністю ρ,
діє рівномірно розподілене навантаження з
інтенсивністю
G
p h g
F
p=ρ g h
h
7.
2. Навантаження від ваги насипу можнавизначити
розподіленим
рівномірно
уздовж безкінечної смуги, а поперек – по
замкненій трапеції.
p
8.
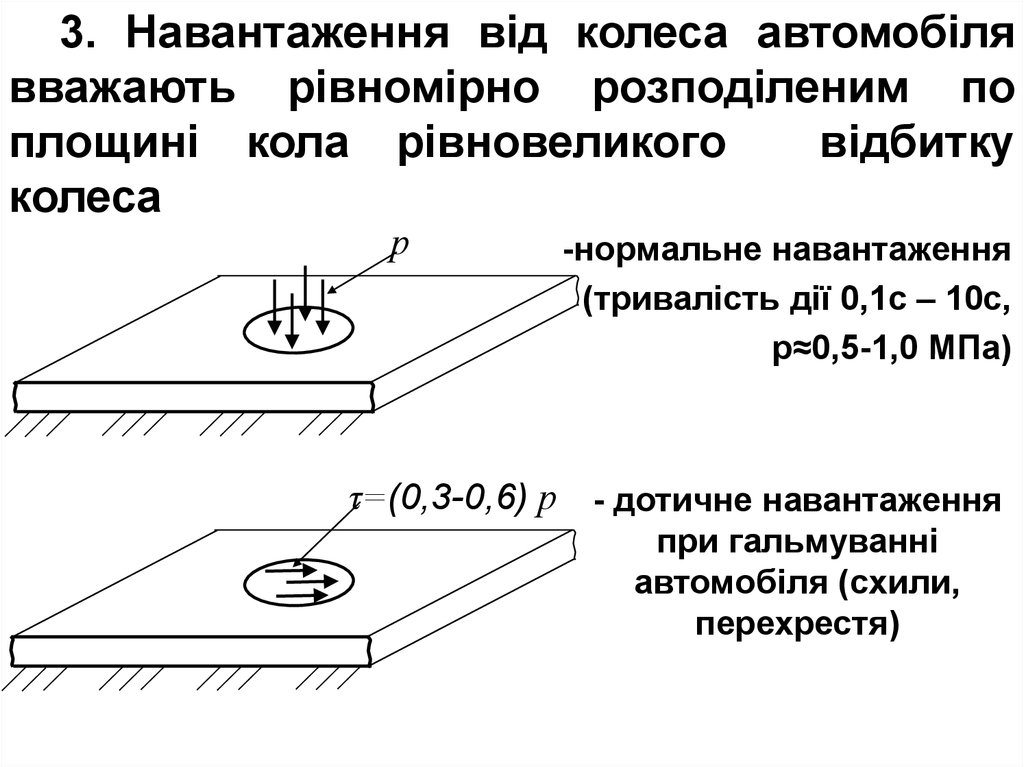
3. Навантаження від колеса автомобілявважають рівномірно розподіленим по
площині кола рівновеликого
відбитку
колеса
р
-нормальне навантаження
(тривалість дії 0,1с – 10с,
р≈0,5-1,0 МПа)
τ=(0,3-0,6) р - дотичне навантаження
при гальмуванні
автомобіля (схили,
перехрестя)
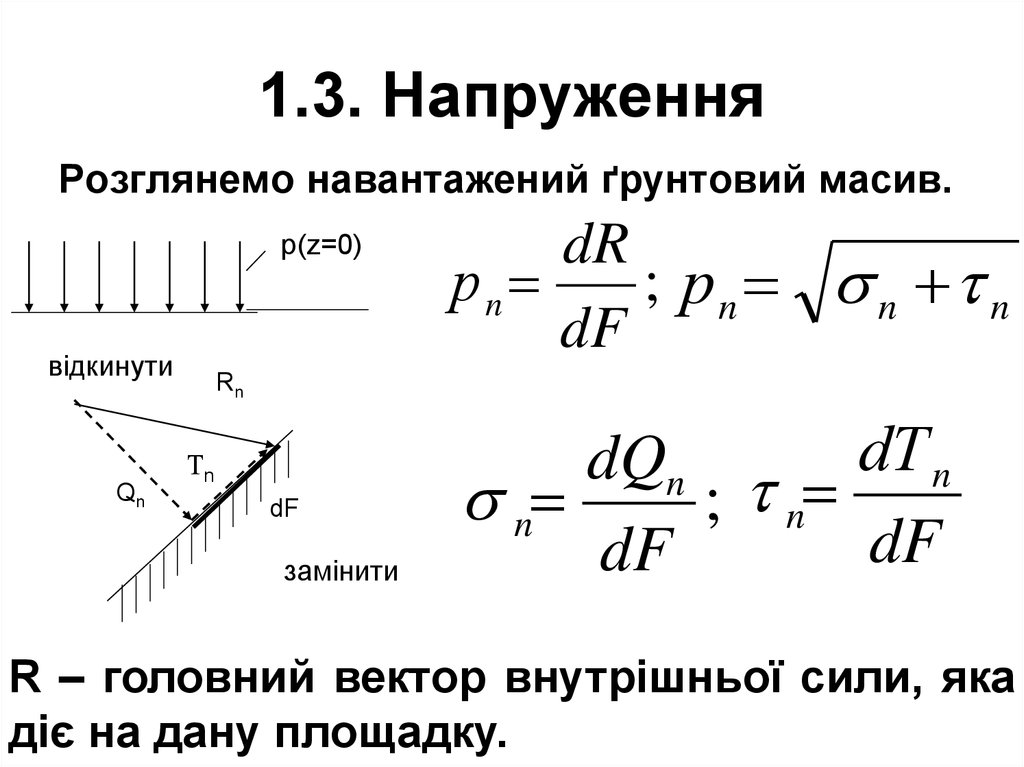
9. 1.3. Напруження
Розглянемо навантажений ґрунтовий масив.р(z=0)
відкинути
Qn
dR
рn
; рn n n
dF
Rn
Tn
dF
замінити
dТ n
dQn
n
; n
dF
dF
R – головний вектор внутрішньої сили, яка
діє на дану площадку.
10.
Якщо через деяку точку ґрунтовогомасиву,
на
поверхні
якого
діє
навантаження р(z=0), провести довільну
площину n і відкинути уявно всю частину
масиву по один бік цієї площини, то
потрібно замінити дію відкинутої частини
на частину що залишилась - відповідною
силою R. Внутрішня сила (рn), яка
приходиться на одиницю площі (Fn),
називається напруженням.
Головний вектор напружень рn зручно
розкласти на складові: σn–нормальне
напруження та n – дотичне напруження.
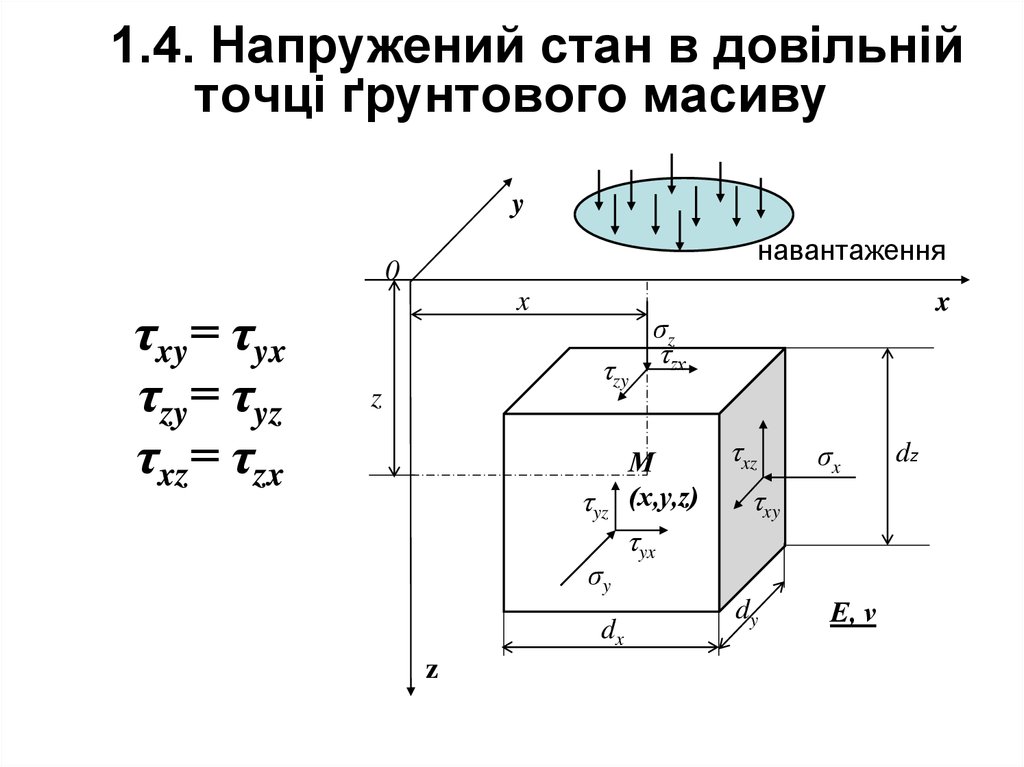
11.
1.4. Напружений стан в довільнійточці ґрунтового масиву
y
навантаження
0
τxy= τyx
τzy= τyz
τxz= τzx
x
zy
z
yz
σy
dx
z
x
σz
zх
М
(х,y,z)
yx
xz
σx
xy
dy
E, ν
dz
12.
Щоб охарактеризувати напружений станв довільній точці М(x,y,z) ґрунтового
масиву, розміщують початок декартових
координат (0) в деякій точці поверхні
масиву, виділяють поблизу точки М
елементарний паралелепіпед з ребрами
dx,dy,dz і позначають σx – вертикальне
нормальне
напруження.
σy,σz–
горизонтальні нормальні напруження. zу,
уz однакові між собою по закону “парності”
дотичних напружень, які діють по гранях
паралельних осі Х; zx, xz – те ж,
паралельних осі У;
xy, yx– те ж,
паралельних осі Z.
13.
Враховуючипопарну
рівність
дотичних напружень, для повної
характеристики напруженого стану
необхідно знайти 3 нормальні і три
дотичні компоненти напружень. Вони
повинні бути встановлені, як функції
координат
точки,
в
якій
визначаються
напруження
і
як
функція величин, які характеризують
навантаження і матеріал масиву
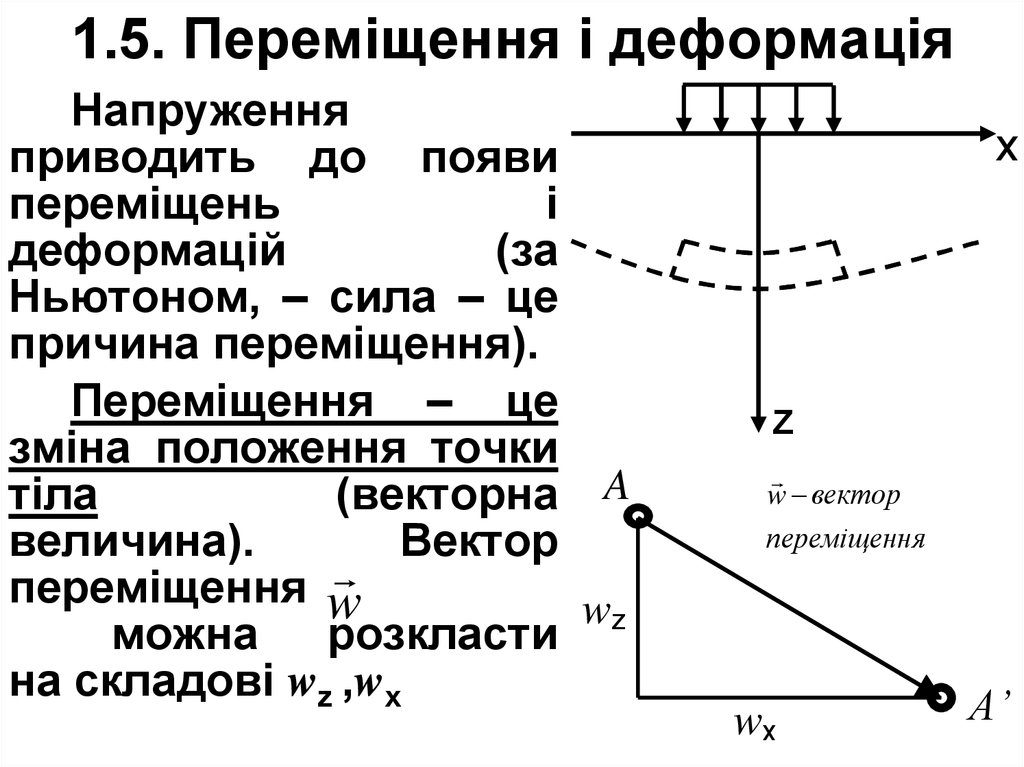
14. 1.5. Переміщення і деформація
Напруженняприводить до появи
переміщень
і
деформацій
(за
Ньютоном, – сила – це
причина переміщення).
Переміщення – це
зміна положення точки
тіла
(векторна A
величина).
Вектор
переміщення w
wz
можна
розкласти
на складові wz ,wх
x
z
w вектор
переміщення
wx
A’
15.
Наприклад,при
рівномірному
навантаженні всієї горизонтальної поверхні
масиву нормальним до неї навантаженням
всі точки цієї поверхні будуть мати
однакові вертикальні переміщення wz.
c
wz
c’
A
Á
wАz
lz
l ́z
В
В́
wВz
Зрозуміло, що точка А
переміститься більше
ніж В, так як вона
“осяде” на стільки ж, і
крім
того
“обіжметься” відрізок
АВ. Тому lz > lz
( тобто Δ lz= lz’- lz <0 стиск)
16.
Деформація– це зміна положення точоктіла відносно одна одній. Деформація
буквально – зміна форми). Наприклад,
при рівномірному навантаженні всієї
поверхні масиву відстань між т.А і т.В
змінилась на
l lZ lZ – абсолютна деформація.
Відношення
Z
l
lZ
– відносна
деформація в напрямку осі z.
17. Деформації і переміщення грунту зумовлені такими процесами:
1) обтиснення частинок і їх агрегатів;2) зменшення оболонки зв’язаної води
в зоні контакту при наближенні
частинок;
3) обтиснення
порової
води
та
повітряних бульбашок;
4) руйнування агрегатів із частинок що
склеїлись і руйнування окремих
частинок;
5) видавлювання вільної води із пор;
6) перепакування
зерен
шляхом
взаємного переміщення.
18.
Переміщення і деформації, зумовленіпершими трьома процесами, оборотні
пружні (elastic) тобто вони зникають після
розвантаження, а зумовлені останніми
трьома процесами – не оборотні (рlastic)
тобто
вони
залишаються
після
розвантаження. Тому повне переміщення і
повна відносна деформація складаються із
пружної (е) і залишкової частин (р) :
w w
(е)
w
(е)
( р)
( р)
19. 1.6. Деформаційні характеристики ґрунту
Механічнівластивості
ґрунту,
які
характеризують його поведінку під дією
навантаження, поділяються на дві групи:
деформаційні та міцнісні. Деформаційні
характеристики
визначають
здатність
ґрунтового масиву змінювати розміри і
форму під дією навантаження. Міцнісні
визначають здатність ґрунту протистояти
дії навантажень.
До
деформаційних
характеристик
відносяться: модуль пружності, модуль
деформації, коефіцієнт пружної поперечної
деформації,
коефіцієнт
поперечної
деформації,
а
також
коефіцієнт
стисливості, просідання, консолідації.
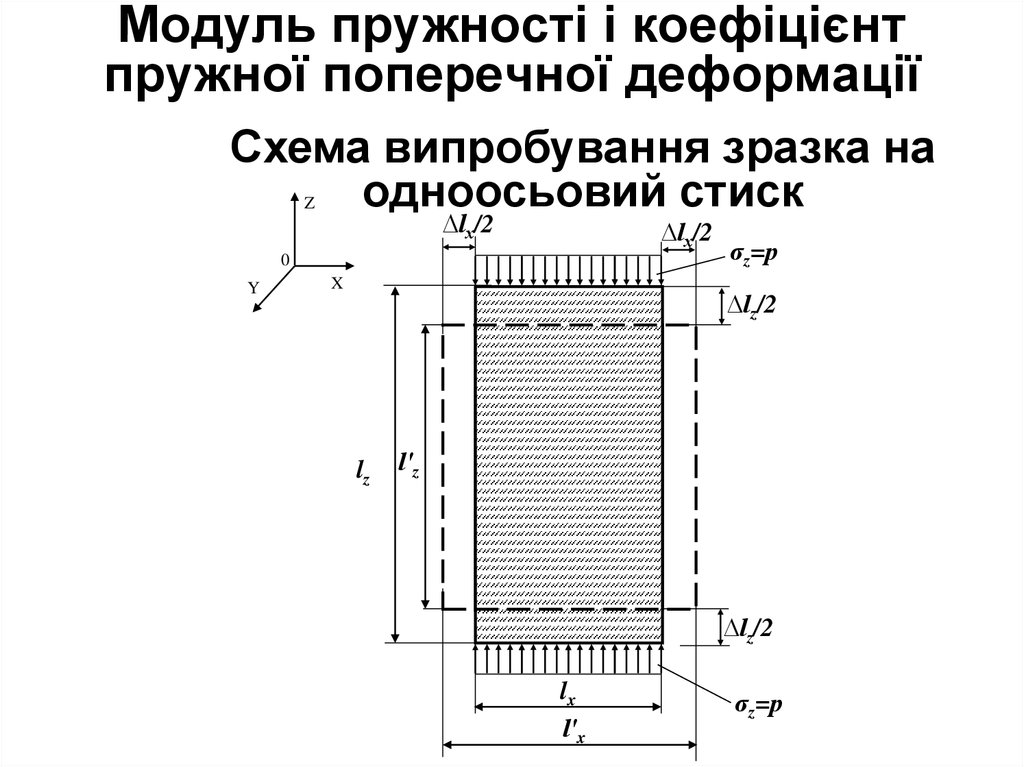
20. Модуль пружності і коефіцієнт пружної поперечної деформації
Схема випробування зразка наодноосьовий стиск
Z
∆lх/2
∆lх/2
0
Y
X
σz=р
∆lz/2
lz
l′z
∆lz/2
lx
l′x
σz=р
21.
При випробуванні грунту на одноосьовестискування нормальне напруження σz
викликає зменшення поздовжнього розміру
Іz до Іz' й збільшення поперечного розміру
ІХ до ІХ'.
Як відомо, абсолютною поздовжньою
деформацією є різниця: lz l l
Z
абсолютною поперечною: lx
відносною
поздовжньою:
відносною
поперечною:
Z
lX lX
Z
l Z
lZ
X
l X
lX
22.
Якщо залишкова деформація відсутня, топовна деформація рівна пружній
.
(е)
( р)
(е)
0
(е)
Досвід показав, що в цьому випадку
тобто при повністю оборотній деформації
для багатьох матеріалів справедливий
закон Гука (Р.Гук –1660р) :
поздовжня
відносна
деформація
пропорційна напруженню, що її викликало
е
Z
Z
Ee
23.
Постійна Ее – називається модулемпружності (модулем Юнга) і є важливою
деформаційною характеристикою пружніх
властивостей матеріалу.
Із закону Гука випливає, що модулем
пружності є відношення поздовжнього
нормального напруження до викликаної
.
ним повздовжньої відносної пружної
деформації
в
умовах
одновісного
напруженого стану :
Z
Eе (е ) .
Z
24. Приклади типових значеннь модуля пружності Ее:
сталь - 200000 МПа,бетон – 30000 МПа,
оргскло – 3000 МПа,
пісок – 100 МПа,
супісок і глина в пластичному стані –
20-100 МПа.
25.
Поздовжняі
поперечна
пружні
деформації також пов’язані одна з одною:
(е)
X
e
(е)
Z
де : νе – постійна, яка називається
коефіцієнтом
пружної
поперечної
деформації (коефіцієнт Пуассона, 1892р).
Коефіцієнтом
Пуассона
називається
взяте з від’ємним знаком відношення
поперечної до поздовжньої відносних
пружніх деформацій в умовах одновісного
напруженого стану
(е)
е
X
(е)
Z
26. Типові значення νе :
сталь – 0,3,бетон – 0,16,
пісок – 0,25,
супісок і суглинок в пластичному стані –
0,35.
Для ідеального пружнього тіла Ее ,νе –
повний набір констант в тому розумінні, що
вони
дають
всю
інформацію
про
властивості
тіла,
необхідних
для
визначення
виникаючих
в
ньому
напружень, переміщень, деформацій при
різних навантаженнях.
27. Зв’язок між напруженням та деформаціями у просторовому напруженому стані
При одновісному напруженому стані колиz 0, х у 0,
z
Закон Гука дає деформації
е
Z
е
Z
Ee
е
e
х у е z e
z
Ee
z
28.
При просторовому напруженомустані:
z 0,
х 0,
у 0,
z
х
х
z
29.
В трьохвимірному напруженому станізалежність між напруженнями та пружними
відносними деформаціями відображається
трьома рівняннями закону Гука (відносні
деформації
визначаються
додаванням
виходячи з незалежності дії сил):
(е)
X
1
X e ( y Z )
Ee
(е)
y
1
y e ( x z )
Ee
(е)
Z
1
Z e ( X y )
Ee
30.
Задопомогою
цих
залежностей
розв’язані різноманітні задачі про
напружено-деформаційний
стан
суцільного середовища і розроблений
потужний апарат розрахунку.
31.
2. Напруженодеформований станоднорідного грунтового
масиву
32.
2.1. Граничний стан в механіцігрунтів
Всі інженерні споруди розраховують
за двома групами граничного стану:
1. По непридатності до експлуатації –
по
міцності,
несучій
здатності,
загальній стійкості;
2. По непридатності до нормальної
експлуатації – по переміщенням, по
місцевій стійкості.
Для цього потрібно вміти знаходити
напруження в грунті
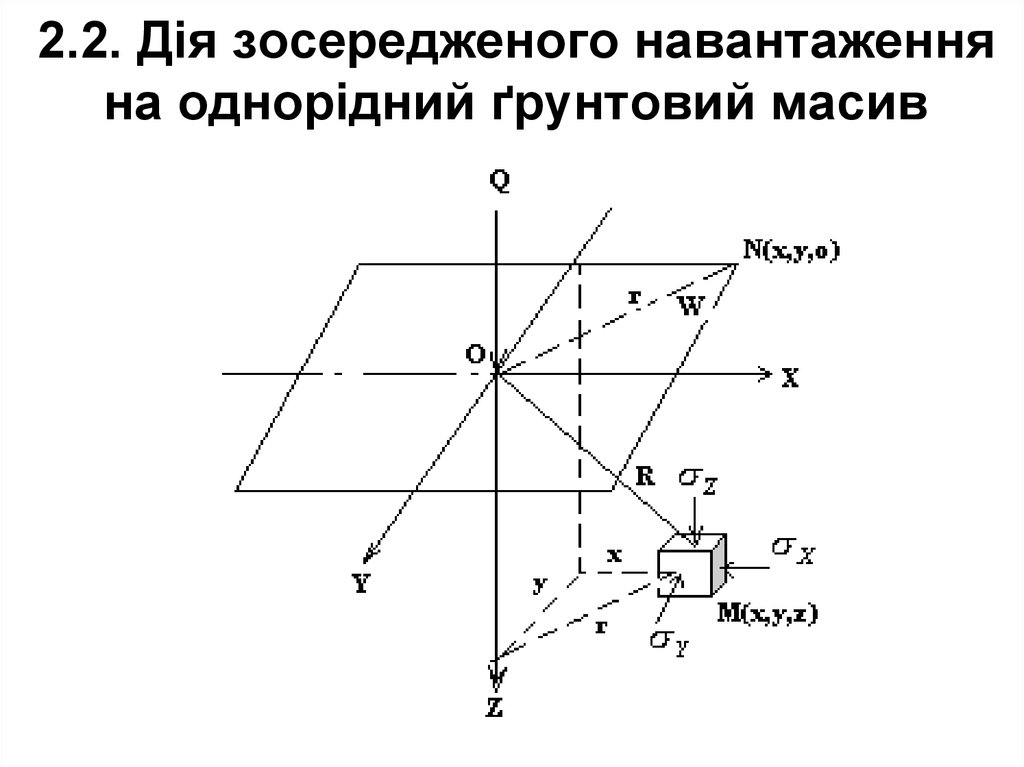
33. 2.2. Дія зосередженого навантаження на однорідний ґрунтовий масив
34.
Розглядається ґрунтовий масив, якийявляє собою однорідний напівпростір –
частина простору обмежена площиною
Х0У.
Матеріал
напівпростору
характеризується модулем Е (пружності
або деформації) і коефіцієнтом поперечної
деформації ν. Вважається, що залежність
між напруженням і деформацією лінійна,
тобто відповідає закону Гука.
В точці, яка співпадає з початком
координат,
прикладене
зосереджене
навантаження перпендикулярне граничній
площині. Потрібно в довільній точці
М(х,у,z)
визначити
напруження
і
переміщення.
35.
Точне розв’язання цієї задачі одержавЖозеф
Буссінеск
–
французький
математик і механік у 1885 році методами
теорії пружності.
Напруження по горизонтальній площині,
паралельній
граничній
площині,
визначається формулами:
3 Q x z
3 Q z
5 ,
z
5 ; zx
2 R
2 R
2
3
3 Q y z
zy
5 .
2 R
2
В механіці грунтів стискуючі нормальні
напруження вважаються додатні “+”.
36.
Вертикальні переміщення точок поверхнімасиву
Q (1 )
.
E r
2
w( r , z 0)
В цих формулах R x y z
- найкоротша відстань від точки, в якій
визначається
напруження,
до
точки
прикладання сили;
2
r x y
2
2
2
2
– найкоротша відстань від даної точки до
лінії дії зосередженого навантаження
(тобто до осі Z).
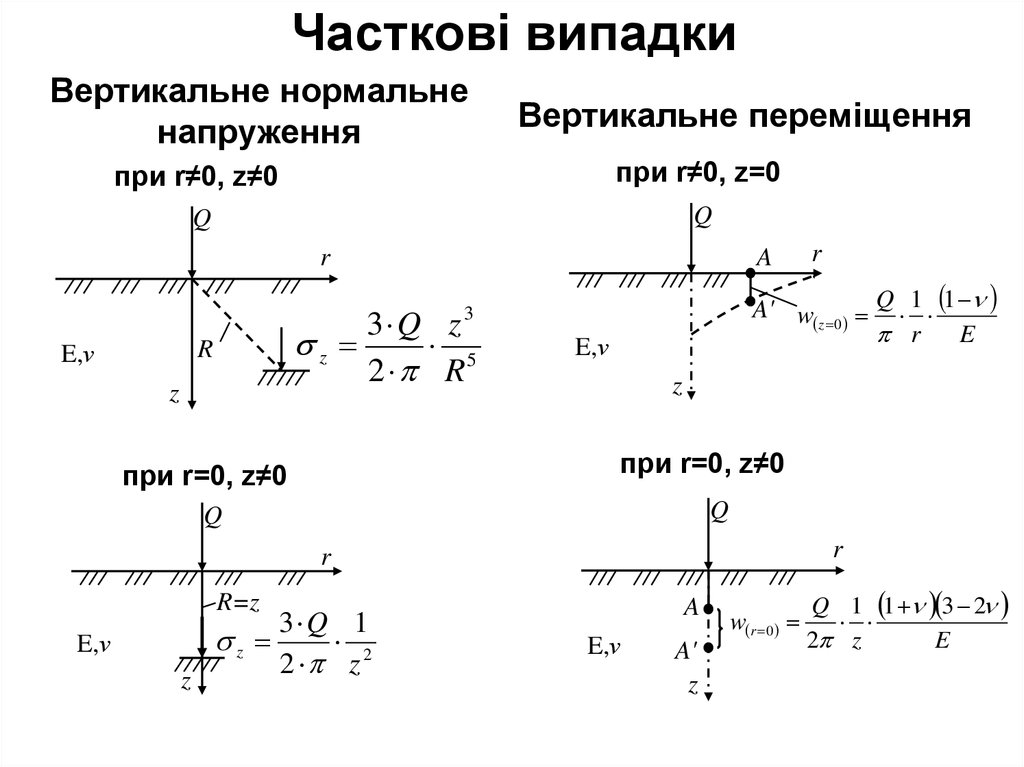
37.
Часткові випадкиВертикальне нормальне
напруження
Вертикальне переміщення
при r≠0, z≠0
при r≠0, z=0
Q
Q
r
A
3 Q z
z
5
2 R
A' w z 0 Q 1 1
r E
3
R
E,ν
z
E,ν
z
при r=0, z≠0
при r=0, z≠0
Q
Q
r
r
R=z
E,ν
z
r
3 Q 1
z
2
2 z
A
E,ν
A'
z
w r 0
Q 1 1 3 2
2 z
E
38.
Із формули Буссінеска випливає, щонапруження по горизонтальній площадці
не залежить від Е та ν, тобто вони не
залежать
від
деформаційних
характеристик матеріалу масиву (грунт,
залізо, пух).
3 Q z
z
5;
2 R
3
3 Q x z
zx
5 ,
2 R
2
3 Q y z
zy
5 .
2 R
2
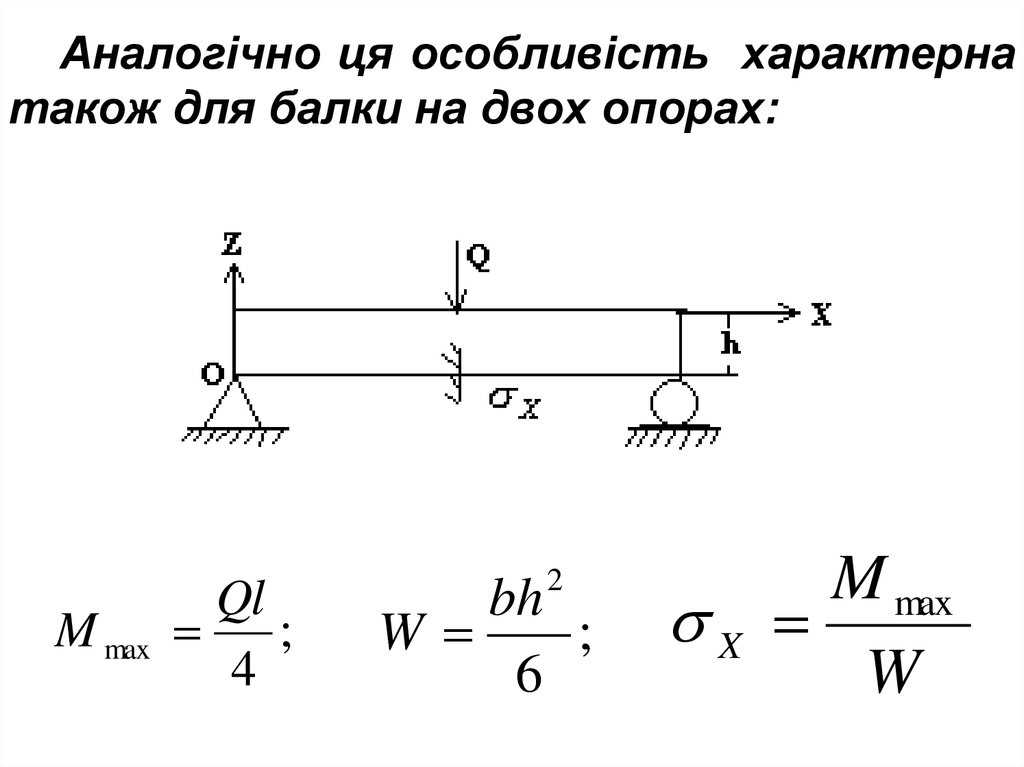
39.
Аналогічно ця особливість характернатакож для балки на двох опорах:
M max
Ql
;
4
2
bh
W
;
6
X
M max
W
40.
Приклад:До горизонтальної поверхні масиву
прикладено
вертикальне
зосереджене
навантаження
400
кН.
Визначити
вертикальне нормальне напруження під
точкою прикладання навантаження на
глибинах 2, 3 і 4 м
Дано:
Q=400 кН; r=0, х=0.
Знайти:
z(z=2 м) - ?; z (z=3 м) - ?; z (z=4 м) - ?
Розв’язок:
3 Q z
За формулою Буссінеска - z
5;
2 R
3
41.
ОскількиR x y z z,
2
2
2
тоді
3
1
1
z
Q 2 0,5 Q 2 .
2 z
z
42.
Таким чиномz 2
1
0,5 400кН 2 2 50кПа 0,05 МПа
2 м
z 3
1
0,5 400кН 2 2 22кПа 0,022 МПа
3 м
z 4
1
0,5 400кН 2 2 12,5кПа 0,012 МПа
4 м
43. Характер епюр σz та wz
44.
Епюри напружень zЕпюри z =f (r)при різних z
Епюра зміни
z (r=0)= f (z)
Q
z=0,050
r
σz
z=2м
0,050
z=0,022
z=0,012
z=3м
0,022
z=4м
0,012
z
45.
Ізобари σz (лінії рівних σz)“цибулина”
напружень
Z соnst
Z
Z
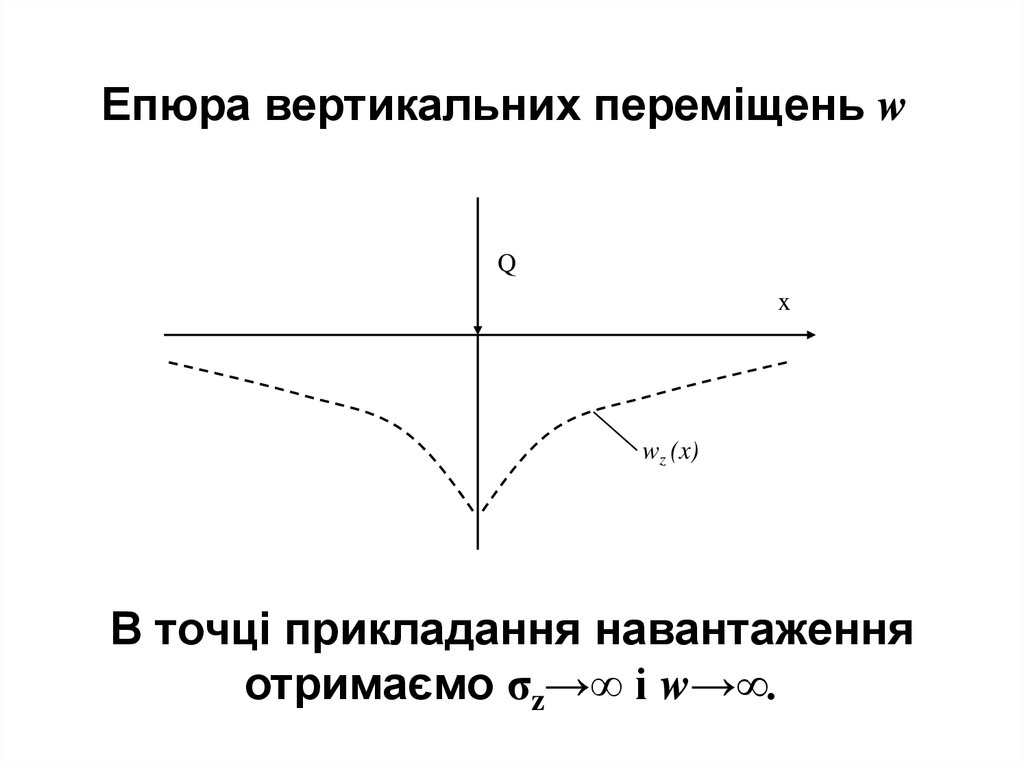
46.
Епюра вертикальних переміщень wQ
x
wz (x)
В точці прикладання навантаження
отримаємо σz→∞ і w→∞.
47.
2.3. Визначення напружень іпереміщень масиву під дією різних
навантажень
Відрізняють
дві
основні
схеми
визначення напружень і переміщення
ґрунтового масиву:
1. Умови плоскої задачі.
2. Умови просторової задачі.
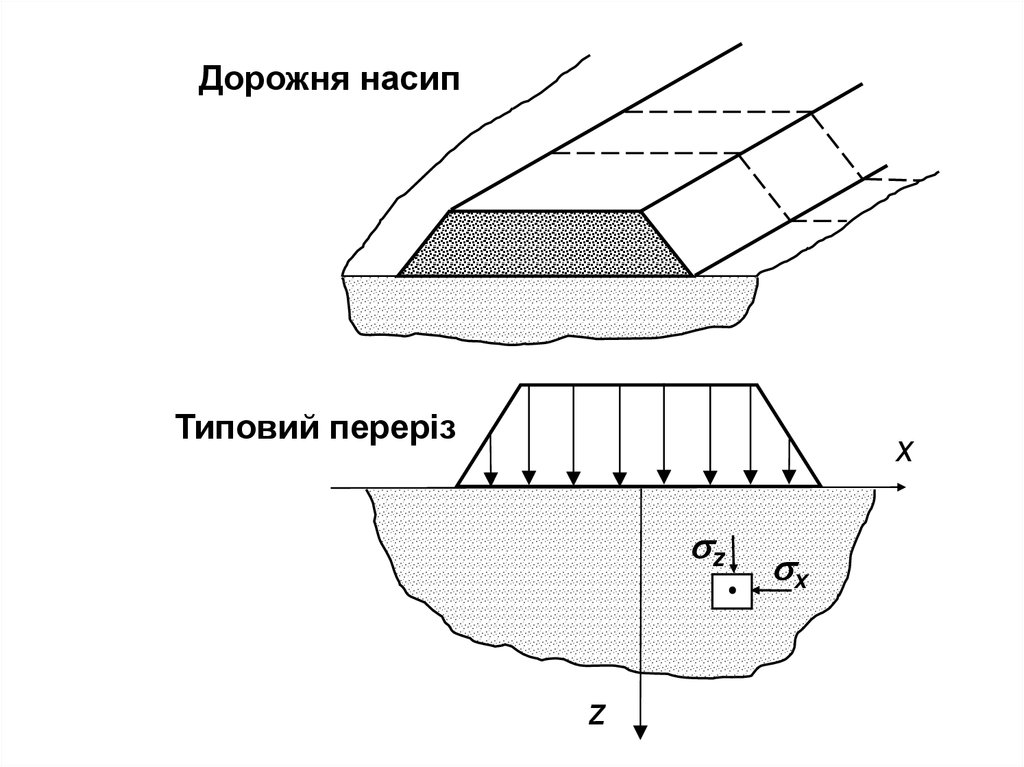
48.
Плоска задачаРозрахункову схему плоскої задачі
використовують у випадках, коли вздовж
однієї із координатних осей навантаження і
напружений стан не міняються. Наприклад,
довжина автодорожнього насипу який має
приблизно постійну висоту, може значно
перевищувати його ширину. Оскільки в усіх
поперечних перерізах насипу і розміщеного
під ним масиву напружено-деформований
стан від власної ваги грунту однаковий,
достатньо визначити його для одного з цих
перерізів. Другим прикладом є стрічковий
або стіновий фундамент.
49.
Дорожня насипТиповий переріз
x
z
z
x
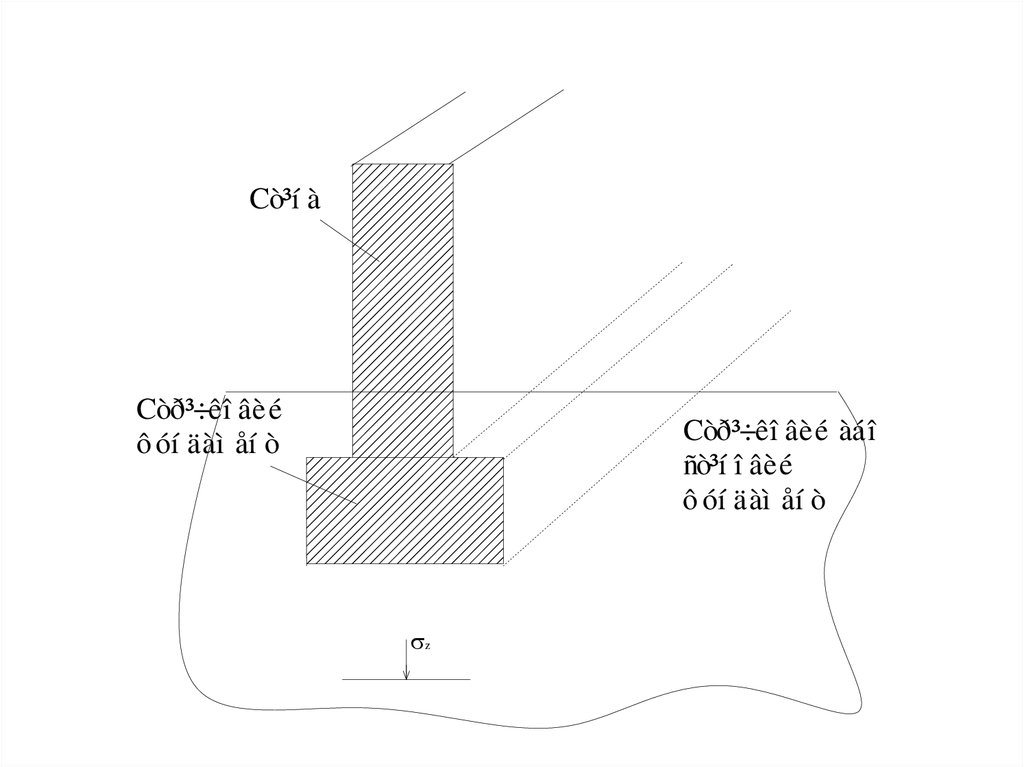
50.
Cò³í àCòð³÷êî âèé
ô óí äàì åí ò
Còð³÷êî âèé àáî
ñò³í î âèé
ô óí äàì åí ò
z
51.
Загальна розрахункова схема плоскої задачіy
b
dQ
q(x)
b
dy
q(ξ)
y
x
0
dξ
ξ
b
b
R
σz
ξ
x-ξ
x
z
z
M(x,0,z)
σx
52.
Нехай вертикальне навантаженнярозподілене по горизонтальній смузі,
яка безмежно простирається вздовж
осі “У” і має ширину 2b уздовж осі “Х”.
По
довжині
смуги
інтенсивність
навантаження не
міняється , а по
ширині міняється по закону q(x).
Вибираємо
типовий
поперечний
переріз площиною ХОZ і визначимо
вертикальне нормальне напруження
у точці М(х;у=0;z).
Z
53.
Для цьоговиділимо на відстані ξ
вздовж осі Х і у вздовж осі У від початку
координат елементарну ділянку поверхні
масиву площею dξdy.
На
цю
ділянку
діє
елементарне
навантаження dQ=q(ξ)dξdy. Будемо його
вважати зосередженим.
54.
Тоді по формулі Буссінеска напруженняdσz в точці М від навантаження dQ буде
3
3
3z dQ
3z
d z
5
q( )d dy,
5
2 R
2 R
де
R (x ) y z
2
2
2
– найкоротша відстань між центрами
елементарної ділянки і точкою в якій
визначається напруження.
55. Інтегруючи це рівняння по осі Х від (– в) до (+в) і уздовж всієї осі Y одержимо
3 в3z
z
2
в
q( )d dy
( x )
2
y z
2
5
2 2
Цей інтеграл визначений для різних
видів навантажень q(x): тобто стосовно
різних видів q(ξ) і є готові таблиці для
здійснення інженерних розрахунків.
56.
Просторова задачаСхему
просторової
задачі
використовують, коли розміри області
прикладання навантаження співрозмірні
між собою: відбиток колеса автомобіля,
опора моста і таке інше.
Напруження
і
переміщення
від
довільного навантаження визначають на
основі
рішення
для
зосередженого
навантаження.
57.
Наприклад, Zвід
дії
зосереджених навантажень:
Q1
Q2
z
3
двох
z
3
3
3Q1 z
3Q2 z
3z Q1 Q2
z
( 5 5)
5
5
2 R1 2 R2 2 R1 R2
58.
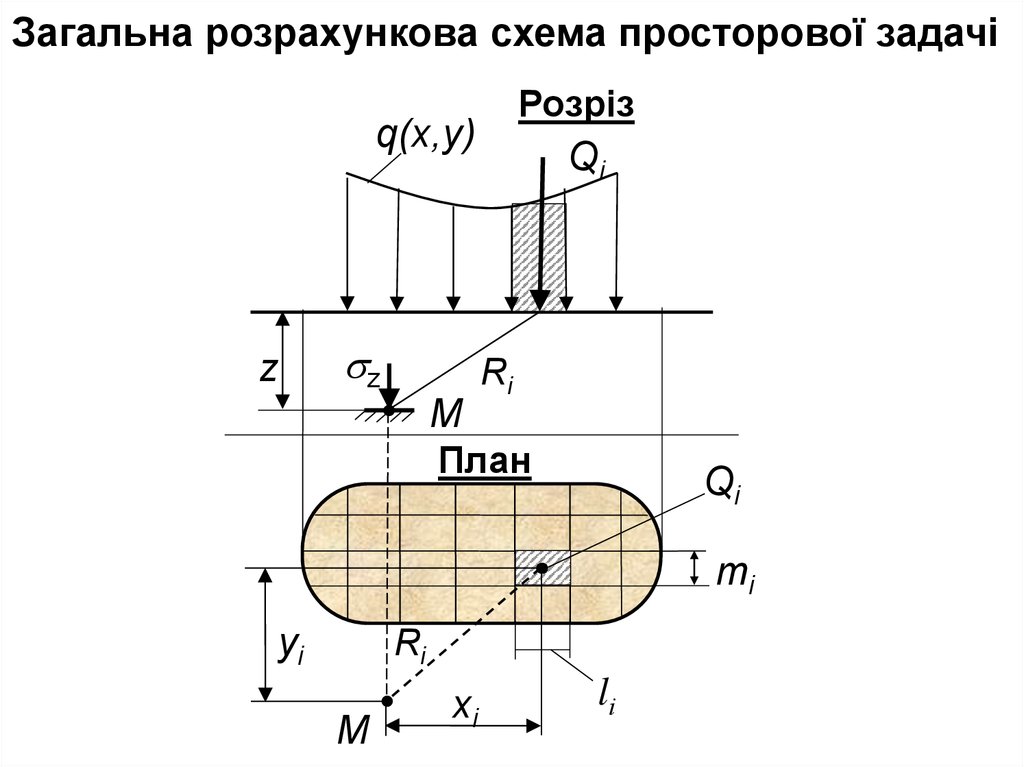
Загальна розрахункова схема просторової задачіРозріз
q(x,y)
z
z
M
Qі
Ri
План
Qі
mі
yі
Ri
M
xі
lі
59.
Напруження в даній точці від довільногонавантаження
визначають
наступним
чином:
всю навантажену площу розбивають на
малі площинки. Навантаження на кожну із
них
Q lmq ,
i
i
i
i
вважають зосередженим:
3
3Z Qi
Z
5.
2 Ri
Визначають від кожної із них напруження
і підсумовують:
n
l i mi q i
3 3
Z
z
5
2 i 1 ( x ) 2 y 2 z 2 2
(z>2mi або z>2li).
60.
Такийметод
необхідно
використовувати для z>2mi або z>2li
Чим більше n, тим вище точність
визначення.
Такий
метод
добре
алгоритмізується,
зводиться
до
повторних операцій і реалізовується на
ПЕОМ.
61.
Дія навантаження, розподіленогопо круговій площі
D
p
z
z
z
z
z(z)
62.
Для розрахунку одягу автомобільноїдороги на міцність, розрахунку основ під
круглим
фундаментом
важливе
значення має випадок дії нормального
навантаження, рівномірно розподіленого
по круговій площі.
63.
В точках, розміщенихнавантаженого
круга,
формули Буссінеска дає:
під центром
інтегрування
1
Z ( x 0' y 0' z ) P 1
3
2
D 2
1 ( )
z2
при z 0, z P
при z , z 0
64.
Максимальнепереміщення (прогин)
штампі:
вертикальне
при гнучкому
p D (1 )
w
;
E
2
при жорсткому штампі:
w
p D (1 )
4
2
E
65.
Приклад:Димова труба ТЕЦ з масою 7850т має
залізобетонних фундамент з круговою
підошвою
діаметром
20
м.
Він
опирається на основу із глинистого
грунту з модулем деформації 20 МПа і
коефіцієнтом поперечної деформації 0,3.
Визначити
вертикальне
нормальне
напруження на глибині 10 м під центром
фундаменту
(вважаючи від його
підошви) і переміщення центра підошви.
66.
Дано:m=7850 т ; D=20 м , ε=20 МПа, v=0.3,
Q mg 7850 10 3 кг 10 м
с
2
78,5МН
Площа підошви
D 2 20 2
F
314 м 2
4
4
Середній тиск на поверхню
грунту під трубою
Q 78.5МН
P
0,25МПа
2
F
314 м
Знайти: Z (Z 10) , w(z=0, r=0)- ?
67.
Розв’язок:1
Z ( Z 10) P 1
3
1 ( 20 ) 2 2
2
10
1
0.25МПа 1
0,16МПа
8
PD(1 2 ) 0,25МПа 20 м (1 0,32 )
W
0,23 м
E
20МПа
68.
3. Напруження вшаруватому масиві та його
осідання
69. 3.1 Напруження в шаруватому масиві від зовнішнього навантаження
У природному заляганні ґрунтовий масивскладається
із
шарів,
деформативні
характеристики яких відрізняються один від
одного, тобто цей масив є шаруватим
(шаруватий
напівпростір).
Типовим
шаруватим
напівпростором
є
також
дорожній одяг автомобільної дороги. Модулі
пружності шарів дорожнього одягу можуть
відрізнятися один від одного на 1-2
порядки. Дорожній одяг влаштовують,
щоб зменшити напруження в ґрунті від дії
колісного навантаження. Його вартість
складає біля 50-70% вартості будівництва
дороги.
70.
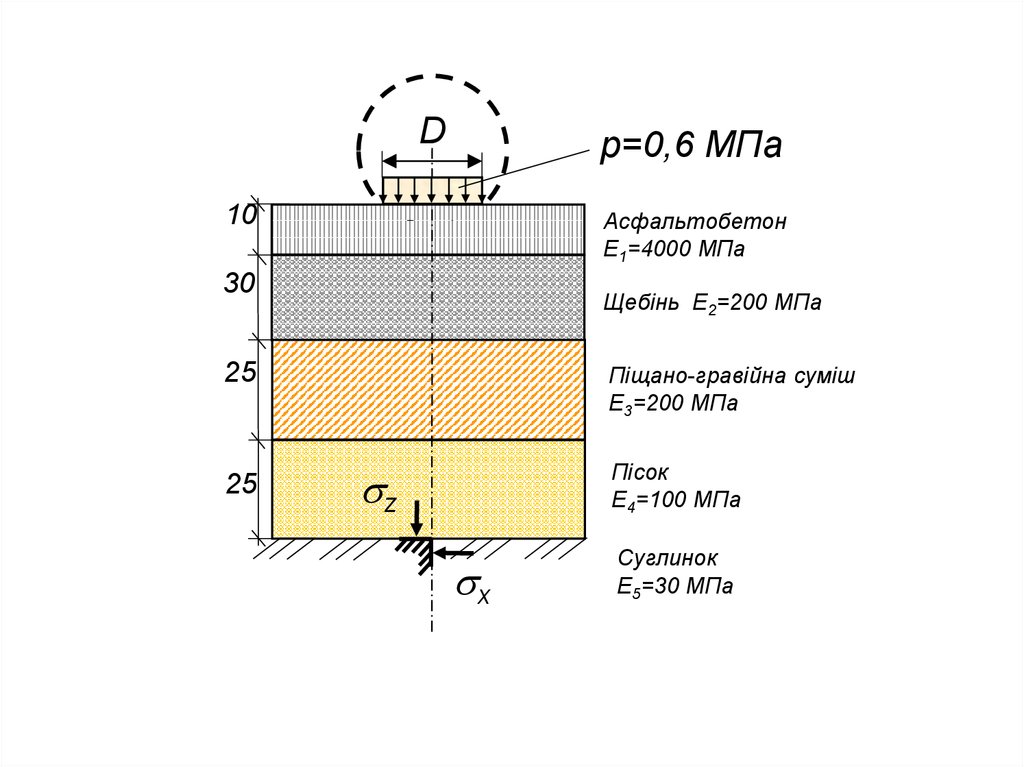
Dр=0,6 МПа
10
Асфальтобетон
Е1=4000 МПа
30
Щебінь Е2=200 МПа
25
25
Піщано-гравійна суміш
Е3=200 МПа
Пісок
Е4=100 МПа
z
x
Суглинок
Е5=30 МПа
71.
Товщини шарів дорожнього одягурозраховують так, щоб напруження, які
виникають в грунті, не перевищували
допустимих за умовою міцності Кулона:
am
1
( 1 3 ) ( 1 3 ) sin C
2 cos
де для точки, яка належить осі симетрії
1 Z , 3 X
Тому для розрахунку дорожнього одягу
на міцність необхідно вміти визначати
напруження в шаруватому напівпросторі.
Є точні вирішення цієї задачі, але вони
складні і можуть бути реалізовані тільки
на ЕОМ.
72.
Для вирішення інженерних задаччасто
використовують
спрощені
розрахункові схеми, що дозволяють
отримати
нескладні
аналітичні
залежності для виконання розрахунків з
достатньою точністю.
При цьому
найчастіше шаруватий
напівпростір
приводять
до
однорідного,
що
дозволяє
використовути прості формули для
напружень
в
однорідному
напівпросторі.
73.
р74.
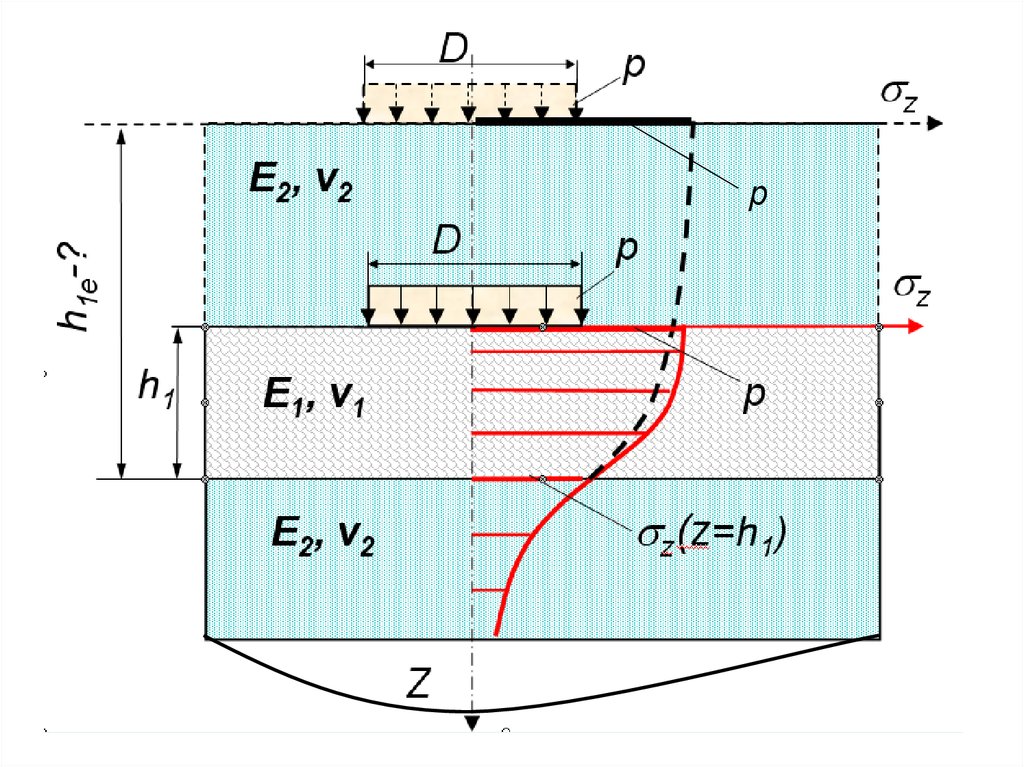
Дляприведення
шаруватого
напівпростору
до
однорідного
знаходять товщину еквівалентного шару
he такою, напруження якої на глибині he
від поверхні однорідного напівпростору
буде дорівнювати
напруженню на
глибині h1 від поверхні шаруватого
напівпростору.
Визначивши he можна знаходити
напруження
в
шаруватому
напівпросторі, користуючись відомими
простими формулами для однорідного
напівпростору.
75.
Одна із таких методик (проф.Г.І.Покровський
і
М.М.
Іванов)
визначення товщини еквівалентного
шару виходить з простого аналізу на
згин балок або плит. Припустимо, що
є балка з прогоном l, матеріал якої має
модуль
пружності
Е1,
висотою
поперечного перерізу h1 і шириною b1.
Потрібно змінити цю балку на балку із
матеріалу з модулем пружності Е2 за
рахунок зміни висоти, не змінюючи
ширину поперечного перерізу, так, щоб
прогин не змінювався.
Якою повинна бути висота h2?
76.
77.
Товщина еквівалентного шару із матеріалунапівпростору по цій методиці приведення
дорівнює
E1
3
he h1
, (10.1)
E2
формула Г.І.Покровського і М.М. Іванова
Однак
формула
Іванова-Покровського
недостатньо точна. Наприклад, при
E1
E2
0
(коли під шаром нескельного грунту
знаходиться масив скельного грунту) вона дає
h
0
,
е
цьому випадку нескельний
тобто в
грунт
начебто не розподіляє напружень (навіть при
збільшенні його товщини).
78.
Ця формула проста, дається впідручниках і широко використовується
в практиці. Однак, при Е1>Е2 вона дає
збільшену hе (тобто занижує напруження
порівняно з фактичним), а при Е1<Е2 дуже
малу еквівалентну товщину hе (тобто
завищує напруження).
Виходячи з аналізу напруженого стану
шаруватого напівпростору професором
Радовським
Б.С
пропонується
інша
методика
його
приведення
до
однорідного. Вона базується на такій
формулі для еквівалентної товщини:
1 E1
he h1 3 1 , (10.2)
2 E2
79.
Приклад №1.Шар грунту, який стискується,
товщиною Н лежить на скельній основі.
На денній поверхні грунту по площі
круга
діаметром
D
розподілене
нормальне
навантаження
з
інтенсивністю р.
Визначити максимальне вертикальне
нормальне напруження
σz на підошві
шару грунту, користуючись рішенням
задачі для однорідного напівпростору,
якщо Н=D.
80.
Дано:Н
р;
D;
Н =D
Знайти:
Н - ? z - ?
D
p
z
Н
z
z(z=H)
81.
Рішення.Для однорідного
напівпростору під
центром навантаження кругової площини
маємо:
1
z р 1
3
D 2 2
1
2 z
, (10.3)
і за формулою (10.1) : Z e H
3
E1
E2
За формулою (10.1) і (10.3) отримаємо при
E2 :
і
Z р
тобто відповідно до формули (10.1) розподіл
напруження відсутній.
ze 0
82.
За формулою (10.2) і (10.3):1 E1
1
3
he H 3 1 H
0.7937 H 0.7937 D
2 E2
2
1
Z P 1
3
D 2 2
1
2Z
1
3
P 1
1 2 2
1
1.5874
0.394 P
За точними розрахунками з допомогою
ЕОМ при 0.5 Z 0.421P
і при
0 Z 0.413P (похибка 5-6%).
83.
Приклад №2.Шар щебеню товщиною h1=30см з модулем
пружності Е1=400МПа опирається на супіщаний
грунт земляного полотна з модулем пружності
Е2=40МПа. На поверхні щебеневого шару діє
нормальне
навантаження,
розподілене
з
постійною інтенсивністю р=0,5МПа по площі
круга
(D=30см).
Визначити
максимальний
вертикальний тиск на грунт земляного
полотна.
D
p
Дано:
h1=30cм
р=0,5 см;
h1=30
E1= 400
D = 30 см;
Е1=400МПа; Е1=40МПа
Знайти:
E2= 40
z- ?
84.
• За формулою (10.1):he 303 400
40
303 10 64.6 см
• За формулою (10.2):
1 400
he 303
1 53.0 см
2 40
Тобто 30 см щебеню по розподіляючій
здатності рівнозначні 65 см або 53 см
супіщаного грунту.
85.
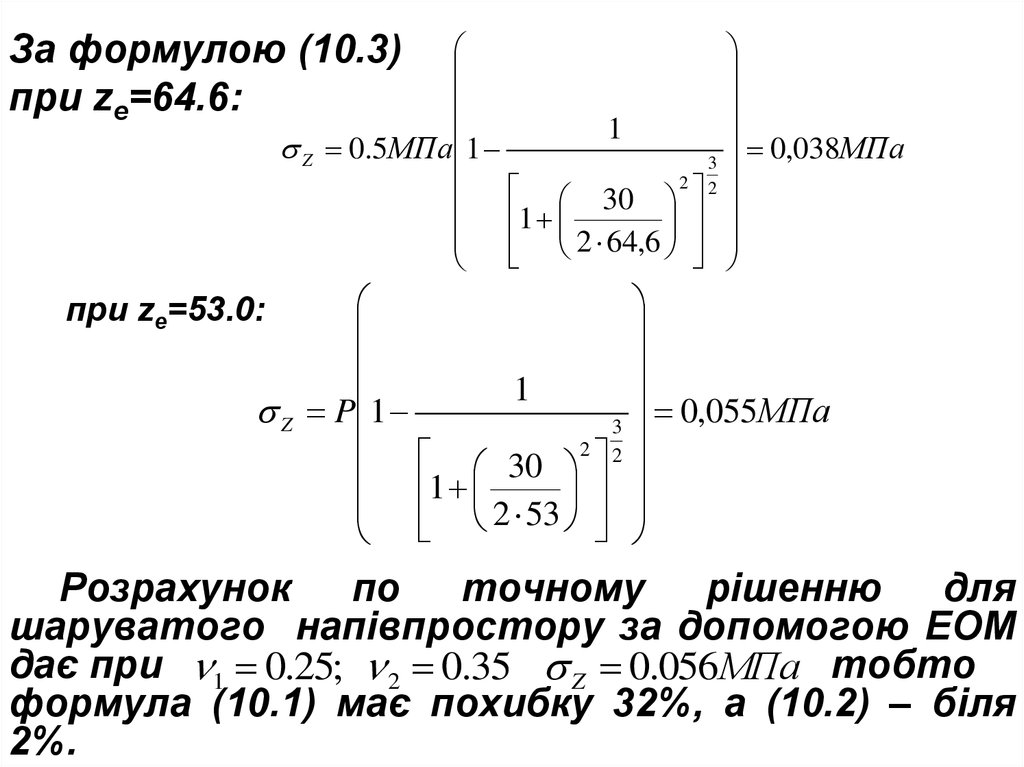
За формулою (10.3)при ze=64.6:
1
Z 0.5МПа 1
3
30 2 2
1
2 64,6
1
Z P 1
3
30 2 2
1
2 53
при ze=53.0:
0,038МПа
0,055МПа
Розрахунок
по
точному
рішенню
для
шаруватого напівпростору за допомогою ЕОМ
дає при 1 0.25; 2 0.35 Z 0.056МПа тобто
формула (10.1) має похибку 32%, а (10.2) – біля
2%.
86. 3.2. Напруження в шаруватому масиві від власної ваги ґрунту
Вертикальне нормальне напруження вшаруватому масиві від ваги ґрунту σzρ
визначають як суму ваги вертикальних
“стовпців”. Які проходять в кожному шарі і
розміщені над горизонтальною площиною
одиничної площі
ρ1
ρ2
ρ3
σ1
h1
σ2
σ3
h2
σzρ h3
σxρ
G1 G2 G3 Fh1 1 g Fh2 2 g Fh3 3 g
F
F
g ( 1h1 2 h2 3 h3 )
n
z g i hi
i 1
де n- число шарів ґрунту, розміщених
вище тієї точки, в котрій визначається
напруження; ρi- щільність ґрунту i-того
шару; hi - товщина i-того шару.
87.
Для грунту, який залягає нижче рівнягрунтової води (РГВ), але вище водоупору,
слід враховувати дію води. По закону
Архімеда вертикальний тиск від одиниці
об`єму грунта :
ρ1g = Csρsg-Csρwg=(ρs-ρw)Csg, але
Vs
1
Cs
,
Vs Vпор 1 e
тобто
( s w )g
i g
1 e
Тому для таких шарів слід замість ρi
підставляти щільність ґрунту :
1
i
si w
1 ei
,
ρ1g=Csρsg-Csρwg+(1-Cs)ρwg =
=Csρsg-2Csρwg+ρwg=g[Cs(ρs-2ρw)+ρw]
88.
Горизонтальне нормальне напруження відвласної ваги визначають з урахуванням
неможливості бокового розширення за
формулою:
x y z ,
де
коефіцієнт
бокового
тиску
1
ґрунту того шару, в якому визначається
напруження; ν - коефіцієнт поперечної
деформації цього шару.
Якщо пробурити свердловину і відкачати
з неї воду, то можна знизити РГВ (хоча б
тимчасово). Тоді товщина шару, в межах
якого присутня виважена дія води
зменшується, власна вага збільшується і
відбувається доущільнення в умовах
природного залягання.
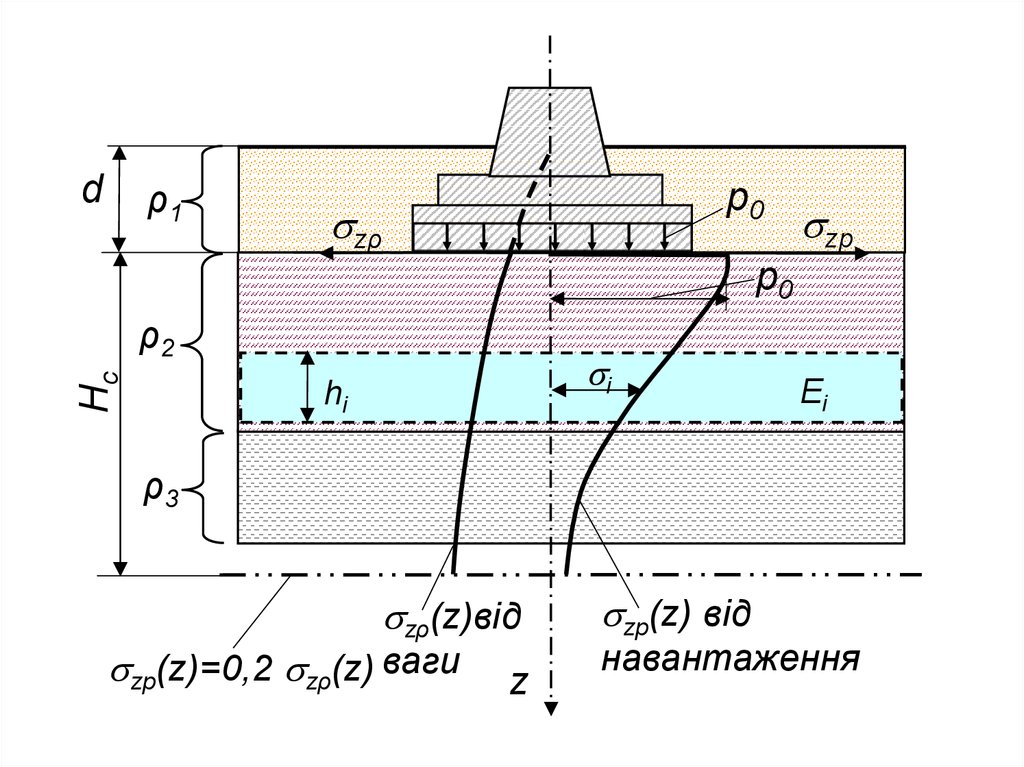
89. 3.3. Визначення осідання шаруватого масиву методом пошарового підсумовування
Вертикальне переміщення (осідання)шарового масиву під дією зовнішнього
навантаження
(наприклад,
від
фундаменту)
визначають
методом
пошарового підсумовування.
90.
dρ1
p0
zρ
zp
p0
Hc
ρ2
i
hi
Ei
ρ3
zρ(z)від
zp(z)=0,2 zρ(z) ваги
z
zp(z) від
навантаження
91.
Припошаровому
підсумовуванні
виходять із наступних положень:
1. Вважають, що осідання викликається
додатковим тиском р0 , який рівний тиску р
під підошвою фундаменту від зовнішнього
навантаження,
виключаючи
тиск
від
власної ваги ґрунту на рівні d закладання
підошви фундаменту р0=р- ρgh тому що
при
влаштуванні
котлованів
для
фундаменту
цей ґрунт був вийнятий і
частина навантаження від власної ваги
ґрунту знята.
2. Напруження σZP на різних глибинах
визначають від тиску ро як в однорідному
масиві (тобто шаруватість при визначенні
напружень не враховується).
92.
3. Товщину ґрунту, який стискується,обмежують глибиною активної зони Нс.
Глибиною
активної
зони
вважають,
починаючи від підошви фундаменту,
глибину
нижче
якої
вертикальне
напруження від навантаження σZP складає
0,2 σZρ, тобто менше 20% вертикального
напруження від власної ваги ґрунту (в
слабому ґрунті (Е<5Мпа) – менше 0,1 σZρ ).
93.
4. Розбивши товщину ґрунту в межахактивної зони на окремі шари з товщинами
hi і модулями Еі, визначають середнє
вертикальне напруження від навантаження
σzpi і в кожному шарі і підсумовуючи
абсолютні деформації стискування шарів,
знаходять осідання W фундаменту за
n
формулою:
h
W
i 1
ZPi i
Eі
де
β=0,8
–
коефіцієнт
стискання
поперечної деформації; n – число шарів, на
які розбита товща Нс, що стикується; σzpi –
середнє
значення
додаткового
вертикального нормального напруження в
і- тому шарі по вертикалі, яка проходить
через центр підошви фундаменту.
94.
Не дивлячись на простоту, цяформула дає хороші результати.
Наприклад,
для
дванадцятиповерхового
житлового
будинку
в
Санкт-Петербурзі
розрахували методом пошарового
підсумовування осідання 31 см, а
заміряне через рік – 35 см.













































































 geography
geography








